Propuesta para recuperar la continuidad del MCS 2015 usando máquinas de soporte vectorial

 

A proposal for recovering MCS 2015’s continuity using Support Vector Machines

 

José Alejandro Ruiz Sánchez
Instituto Nacional de Estadística y Geografía (INEGI), jose.ruiz@inegi.org.mx

Nota: se agradece la colaboración e ideas proporcionadas por Miriam Romo y Benito Durán.

 

Vol. 9 número especial – Epub                                Propuesta para recuperar… – Epub

Debido a procesos de mejora llevados a cabo durante el levantamiento de la información del Módulo de Condiciones Socioeconómicas (MCS) 2015, la distribución del ingreso corriente total cambió de manera sustantiva con respecto a lo que se venía observando en levantamientos previos. Esta propuesta intenta recomponer la continuidad, modificando la representatividad que tenía un hogar en el 2015, de acuerdo con su asignación a un decil pronosticado o artificial creado a partir de un conjunto de variables monetarias y no-monetarias. Para asignar un hogar a un decil artificial, se usó una máquina de soporte vectorial. Como conjunto de entrenamiento se usaron los levantamientos ENIGH-MCS 2010, 2012 y 2014. Una vez realizada la imputación de deciles se ajustaron los factores de expansión de cada hogar, esto permite que hogares con ingresos bajos sean sobreexpandidos y que, para hogares con ingresos altos, su factor de expansión sea reducido.                                 Palabras clave: Módulo de Condiciones Socioeconómicas; MCS; continuidad; SVM; factores de expansión.

Due to improvements in the Socio-economic Module’s data collection 2015 (MCS 2015 by its Spanish acronym), the total income distribution shifted from what has been observed in recent years. Consequently, it is no longer possible to make income comparison with previous information. This methodology is intended to recompose continuity by modifying household weights in 2015, according to its classification into some artificial decile generated by monetary and non-monetary variables. To classify a household we use a technique called Support Vector Machine (SVM) and historic data (2010-2014) as a training data set. Once an artificial decile is imputed to a household in the MCS 2015, we modify its weight so that adding them up by decile represent 10 percent. This allows low-income households to be overexpanded and high-income households to be underexpanded.                                                                                                                                                                          Key words: Socio-economic Module; MCS; Continuity; SVM; weights.

 

1. Introducción

La información relacionada con los ingresos de los hogares captada en el Módulo de Condiciones Socioeconómicas (MCS) 2015 perdió continuidad con levantamientos anteriores del mismo módulo; sin embargo, ello no invalidó ni volvió erróneos o sesgados los datos obtenidos. Es en este sentido que el problema de continuidad histórica puede ser abordado como uno de (re)clasificación de hogares, donde los conjuntos generados estén constituidos por observaciones con características similares.

Una manifestación de la pérdida de continuidad entre levantamientos con respecto a variables de ingresos se dio al realizar análisis por deciles: las tasas de crecimiento del 2014 al 2015 del ingreso corriente total (ICT) de cada decil fueron muy superiores a las que se venían observando históricamente.

El acercamiento metodológico en este documento consiste en pronosticar el decil al cual debería pertenecer cada hogar en el 2015 a partir de información monetaria y no-monetaria, de forma tal que los hogares que pertenezcan a determinado decil sean consistentes con hogares en deciles iguales, pero de años anteriores. Con base en esta clasificación pronosticada o artificial, se hace un ajuste en los factores de expansión para otorgarle mayor o menor peso a cada hogar, de acuerdo con el decil al que haya sido asignado. De esta forma, hogares con ingresos bajos tendrán un mayor peso muestral que el que tenían originalmente, contrario a los de ingresos altos, quienes verán disminuido su peso muestral. Para pronosticar el decil de pertenencia de los hogares en el 2015, se utilizaron técnicas de Machine Learning para clasificación, específicamente máquinas de soporte vectorial (SVM, por sus siglas en inglés).

Así, la presente propuesta se desarrolló con el objetivo de generar una base de datos alternativa al MCS 2015 que recomponga la trayectoria histórica del ingreso y que tenga como prioridad el no modificar lo declarado por los hogares. Para lograr cambios, entonces, se adecuarán los factores de expansión de tal forma que se modifique la representatividad original que tiene el ingreso declarado. El cambio en los factores de expansión se hará a partir de asignar un hogar a un decil pronosticado, al que teóricamente debería pertenecer, de acuerdo con valores que este hogar reportó sobre un conjunto de variables monetarias y no-monetarias. Por otra parte, y como consecuencia, cuando se usan los nuevos factores de expansión, es posible que la representatividad de subgrupos poblacionales en los cuales se basó el diseño muestral se vea alterada.

El documento se encuentra organizado en seis capítulos; en el segundo de ellos se presenta una descripción de los datos que dan sustento a la propuesta metodológica. En el tercer apartado se desarrolla la técnica de SVM, que es utilizada para la categorización y pronóstico; además, se muestra la forma para modificar los factores de expansión. En el cuarto capítulo se presentan resultados desglosados por entidad federativa y por decil. En el quinto apartado se realiza una validación de la técnica con años anteriores y en el último se muestran las conclusiones.

2. Marco teórico

Características propias al levantamiento del MCS 2015 generaron que la distribución del vector de ingresos se recorriera de manera importante con respecto a años anteriores (ver figura 2.1).

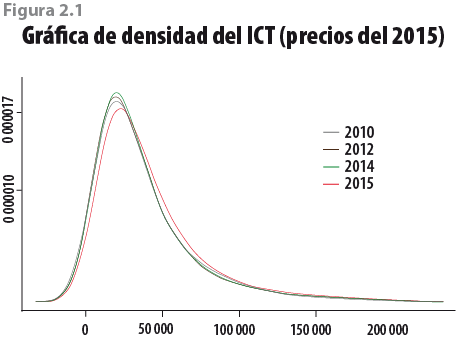
Ello implica que al hacer comparaciones que consideren agrupaciones a través de ingresos (como decilizaciones) se estén mezclando grupos con niveles de ingreso muy distintos. En el caso de las comparaciones por deciles del MCS 2014 y del MCS 2015 se están incluyendo hogares en un decil que, bajo otras circunstancias de recolección de información, pertenecerían a otro (ver figura 2.2).

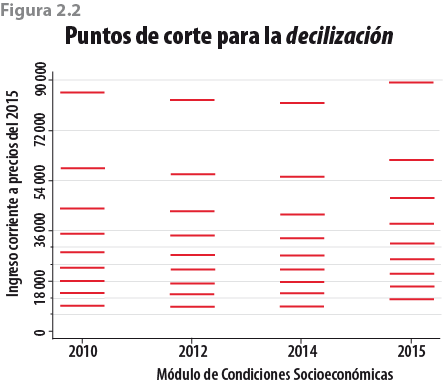
El mecanismo que permita usar información del MCS para generar mediciones consistentes en el tiempo debe incluir el comportamiento histórico de los datos para realizar algún tipo de ajuste en el MCS 2015. Si bien un camino es el ajuste directo al vector de ingresos, la propuesta del presente documento contempla respetar la información proporcionada por los hogares, actuando por medio de la modificación de los factores de expansión. La idea intuitiva del método es generar continuidad a través de la imputación (a cada hogar del 2015) del decil de pertenencia, usando el comportamiento histórico (2010, 2012 y 2014) de decilización y la relación que guarda éste con variables monetarias y/o no-monetarias.

Este método será efectivo en la medida en que las técnicas de clasificación sean certeras y en que los ajustes en los factores de expansión hagan que los hogares de determinado decil x sean representativos de los hogares que, bajo circunstancias similares a las de levantamientos anteriores al 2015, hubiesen pertenecido al mismo decil x.

3. Metodología

3.1 Su aplicación

Existen distintos métodos que permiten pronosticar la clasificación de nuevas observaciones con base en parámetros calibrados a partir de una base de datos alterna donde las observaciones ya se encuentran categorizadas. Un conjunto de estos métodos se encuentra en lo que conocemos como Machine Learning, así como en la estadística clásica; algunos de ellos son: análisis discriminante lineal (LDA, por sus siglas en inglés), redes neuronales artificiales (ANN, por sus siglas en inglés), árboles de decisión, SVM y regresión logística multinomial, entre otras.

Aunque se utilizaron distintas técnicas para comparar niveles de precisión, solo desarrollaremos la técnica SVM, ya que los resultados que se presentan son con base en ella y por haber sido la que generó resultados aceptables de manera consistente bajo diversas especificaciones. La idea intuitiva de SVM es generar hiperplanos separadores que permitan identificar aquellas observaciones pertenecientes a una misma categoría (ver figura 3.1a).

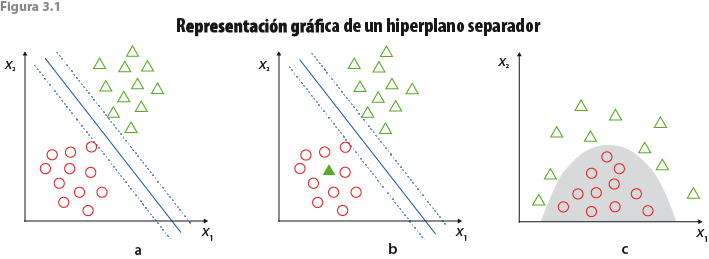
Para su construcción, los hiperplanos deben ser tales que se tenga el menor error de clasificación; es decir, las clasificaciones pueden no ser perfectas (ver figura 3.1b). Para pronosticar la clasificación de una observación nueva, primero se entrena a la máquina con una base de datos ya clasificada y, a partir de los resultados, la máquina decide el grupo de pertenencia de la nueva observación.

De manera formal,¹ sea un conjunto de N parejas (x₁ , y₁ ), (x₂ , y₂ )…(x_N, y_N), donde x_i ∈ R_^p y y_i ∈ {–1, 1}.La variable y_i define la categoría de pertenencia y x el conjunto de covariables.

Sea el hiperplano definido por:

(1)

donde . Una regla de clasificación está dada por la función signo: G(x) = signo[x^T β+β₀ ]. En el caso de clases totalmente separables, existe una función:

, tal que
(2)

y, por lo tanto, podemos encontrar el hiperplano separador que tenga la mayor distancia con respecto a los puntos. A tal distancia se le conoce como margen (M).

Entonces, el problema de optimización sería el siguiente:

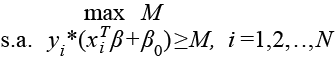(3)

Cuando no puede darse una separación perfecta de las clases, se permite que algunos puntos se encuentren mal clasificados a través de la siguiente especificación:

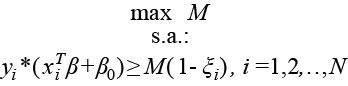(4)

y , donde C es una constante

cuya reformulación en términos de β quedaría de la siguiente forma:

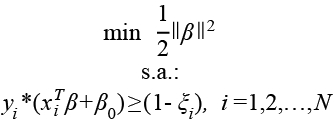(5)

y , donde C es una constante

Formamos la función de Lagrange con sus respectivos multiplicadores α_i , μ_i .

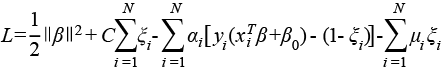(6)

que en su forma más conocida es representada como:

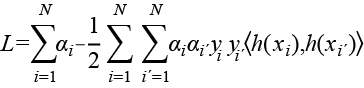(7)

donde K(x,x´) =〈h(x),h(x´)〉 es la función kernel, la cual puede tomar diferentes especificaciones para ampliar el espacio de las covariables. Las especificaciones más comunes son las siguientes:

Lineal

Polinomial de grado d

Radial

Dos de estas funciones Kernel permiten capturar no linealidades como las de la figura 3.1c.

Para extender la metodología al caso de Q clases, existen diversos enfoques, dos de los más usados se explican a continuación: enfoque de clasificación uno vs. uno, construye SVM´s, cada uno del cual compara un par de clases. Para clasificar una observación nueva se usan los clasificadores y se cuenta el número de veces que dicha observación cae en cada una de las Q clases. La clasificación final se hace asignando la observación nueva a aquella clase a la cual fue asignada más veces. El segundo es el de clasificación uno vs. todos, en el cual se realizan Q SVM´s, comparando una clase con las Q-1 restantes; una nueva observación x* será asignada a aquella categoría para la cual es mayor.

En nuestro caso utilizaremos como datos de entrenamiento los deciles (que tendrán el rol de clases o categorías) y las covariables a nivel hogar de los MCS 2010, 2012 y 2014;² con esta información se entrena a la máquina para que aprenda a realizar la decilización y ese aprendizaje será aplicado a la base de datos del 2015, de tal forma que la máquina de soporte vectorial asignará un decil pronosticado x a un hogar en el 2015, siempre y cuando los niveles de las covariables para ese hogar sean similares a aquellos hogares pertenecientes al mismo decil x en años anteriores.

La base de datos de la cual partimos para la decilización artificial es aquella proveniente del artículo “Ajuste demográfico por imputación” (publicado en este mismo número especial de Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía, y cuyo objetivo es únicamente reconstituir la estructura demográfica del MCS 2015). Una vez obtenido el vector de deciles pronosticados, la siguiente etapa consiste en modificar los factores de expansión, de forma tal que hogares con menores ingresos estén sobrerrepresentados y hogares con ingresos mayores sean subrepresentados.

La forma de reasignar pesos muestrales está basada en los deciles pronosticados a los que pertenece cada hogar: cuando un hogar es asignado a un decil pronosticado o artificial x, esa asignación no considera el factor de expansión de dicho hogar y, por lo tanto, no considera el número de hogares a los que representa. Por otra parte, y dado que los montos del ingreso corriente que definen los cortes de la decilización son similares durante el periodo del 2010 al 2014 y que son visiblemente superiores en el 2015 (ver figura 2.2), la decilización artificial (la cual considera el comportamiento histórico) categorizará en el decil I a un número de hogares que representarán menos del 10% poblacional, de acuerdo con sus factores de expansión; es decir, el número de hogares muestrales que la máquina de soporte vectorial asignará al decil I será menor al número de hogares que caen en el mismo decil I cuando se consideran los datos del MCS 2015. Dado que ese menor número de hogares en el decil I representa menos del 10% poblacional, habrá que incrementar sus factores de expansión; esto permitirá que hogares con ingresos más bajos sean sobreexpandidos, mientras que los de ingresos mayores verán disminuidos sus factores de expansión; es decir, que representarán a una menor cantidad de hogares.

Cabe mencionar que esta decilización artificial solo se utiliza en esta etapa de modificación de factores de expansión; una vez creados los nuevos factores, nos olvidamos por completo de los deciles artificiales. Para la decilización final, usada en los análisis de resultados de la cuarta sección, se recurrió al vector de ingreso corriente total, pero incorporando los nuevos factores de expansión.

De manera formal: sea un hogar h y fh su factor de expansión, al formar deciles se debe cumplir que:

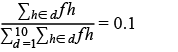(a)

para cada decil d. Sin embargo, dado que los factores de expansión no son considerados en la decilización artificial, nada garantiza que se cumpla la igualdad (a) al utilizar la técnica de SVM para categorizar hogares ya que, en este caso, el número de hogares pertenecientes a cada decil se asigna a partir de un criterio de optimización, donde la condición (a) no tiene rol alguno; por lo tanto, para cumplir con la condición del 10% se generará un nuevo vector de factores de expansión fh⁽ⁿ⁾ , el cual resultará del ajuste a los factores de expansión originales del MCS 2015.

Sea h un hogar perteneciente al MCS 2015 y sea fh el factor de expansión original asociado a ese hogar. Denotemos como h_d,svm a un hogar que fue clasificado en el decil d utilizando la técnica SVM (decil pronosticado).

Entonces, el factor de ajuste para los hogares del decil pronosticado d se define como:

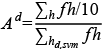
y el nuevo factor de expansión para un hogar que pertenece al decil pronosticado d, es:

Este proceso se realiza para cada una de las entidades federativas por separado, con lo cual se procura cuidar la representatividad por entidad en el agregado nacional.

3.2 Nota técnica

• El software estadístico que se utilizó para la metodología descrita en el apartado anterior fue R, a través de su IDE RStudio versión 1.0.44. Las librerías usadas fueron MASS y NNET. Para el caso particular de la función SVM, el kernel usado fue el lineal, con los parámetros por default.
• Se utilizaron los MCS 2010, 2012 y 2014 como base de datos de entrenamiento para el algoritmo de SVM.
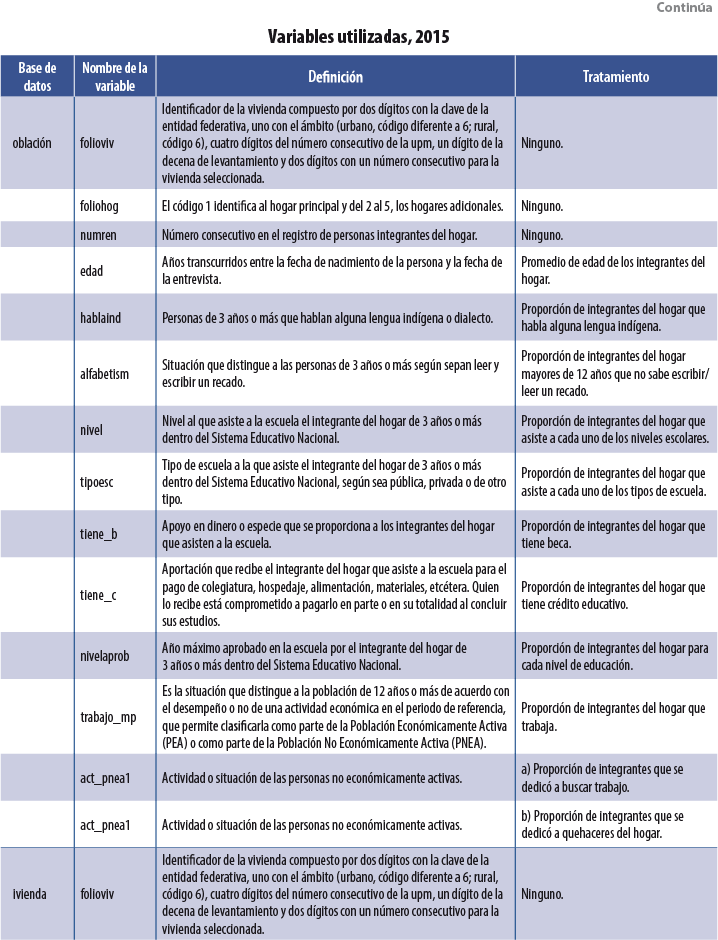
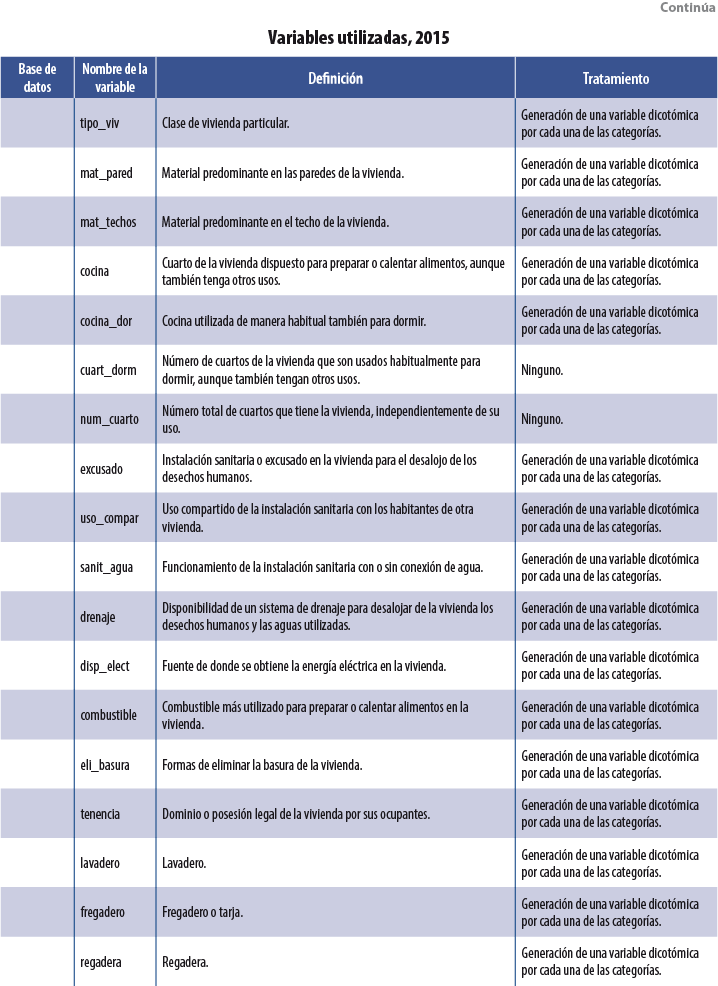
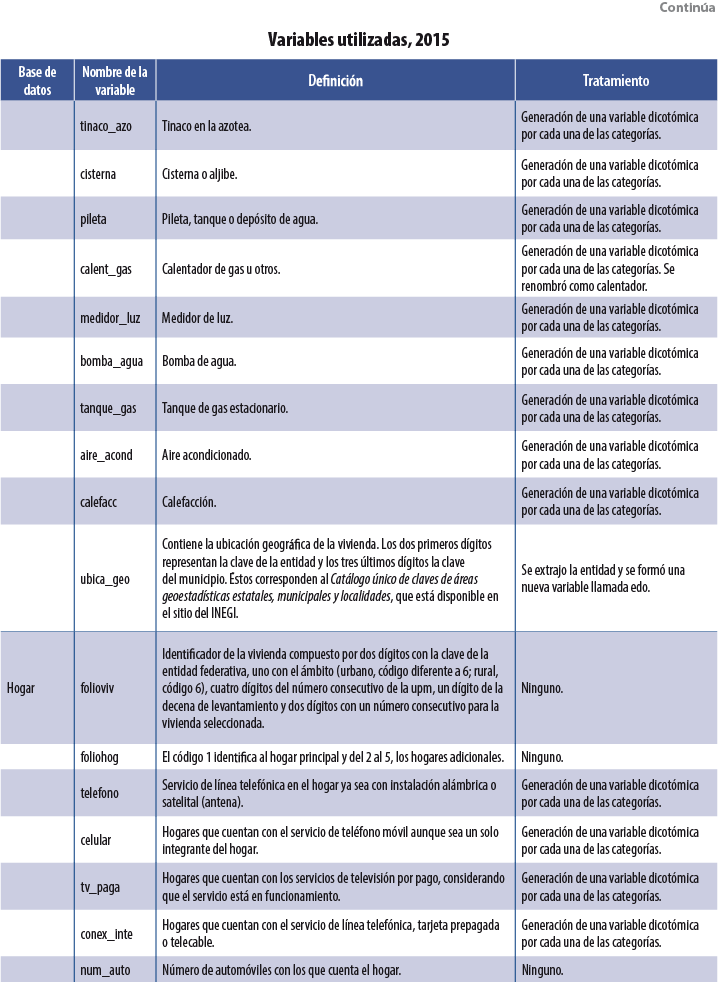
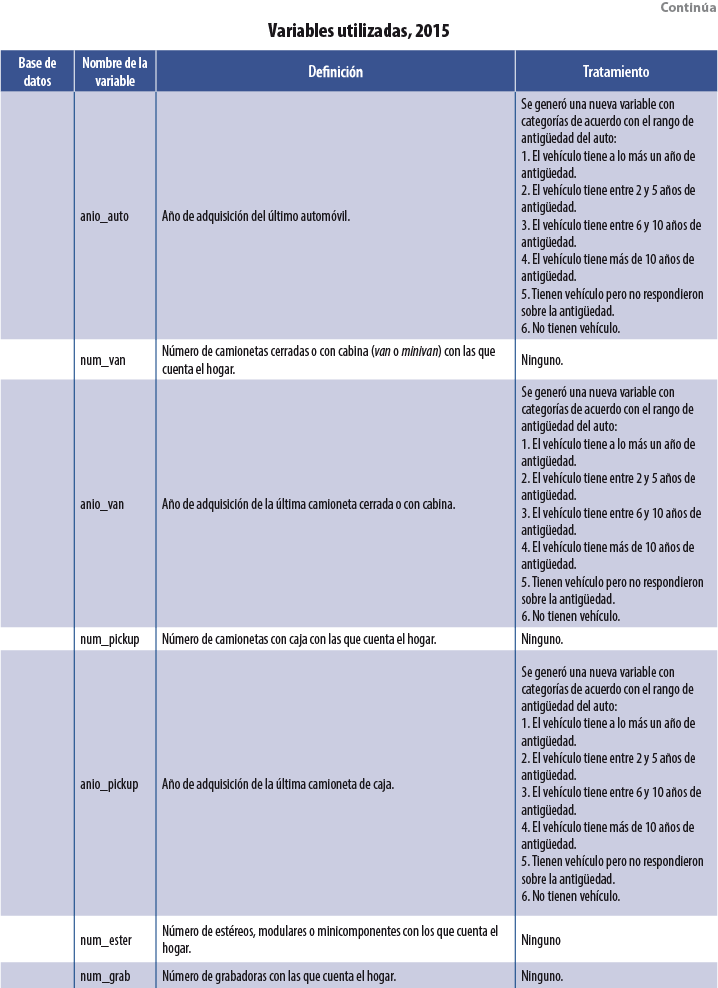
  Se usaron tres bases de datos dentro de cada MCS: población, vivienda y hogares. De la segunda se utilizaron variables asociadas a las características físicas de la vivienda, como: tipo de piso, paredes, dotación de agua, etcétera. De la tercera se emplearon tanto el ICT como variables sobre la pertenencia de bienes muebles (autos y televisores, por ejemplo). Por último, de la base de población se usaron índices por hogar sobre características sociodemográficas de sus integrantes: proporción de miembros del hogar que se encuentran estudiando primaria, promedio de edad de los integrantes, proporción de integrantes que cuentan con estudios universitarios, etcétera. La tabla del Anexo contiene una descripción de las variables usadas en el 2015, así como el tratamiento que se les dio para su incorporación como covariables dentro de las diversas técnicas³ de Machine Learning usadas. Para los MCS 2010, 2012 y 2014 se utilizaron las mismas variables.

4. Resultados

4.1 Resultados a nivel nacional, por entidad federativa y por decil con la nueva base del MCS 2015

Una deducción de la lectura del apartado 3 es que a nivel microdatos no se afectó el vector de ingresos reportado por los hogares; son los cambios en los factores de expansión por hogar los que permiten tener resultados distintos a los del MCS 2015.

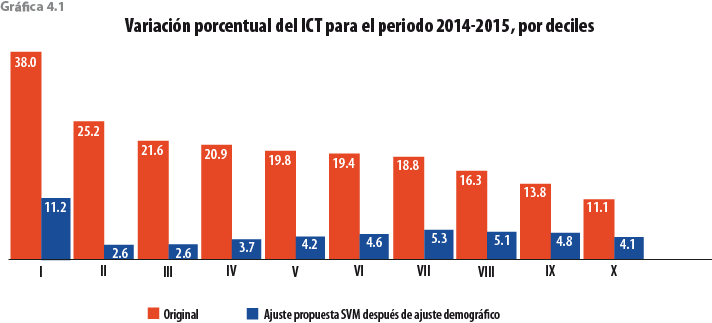
En esta sección se muestran los principales cambios respecto al ingreso y la pobreza bajo distintos niveles de agregación. La gráfica 4.1 muestra los efectos en el ICT por decil. Con respecto al 2014, el MCS 2015 presentó un incremento de 15.6% en el ingreso corriente total, mientras que con la presente propuesta de ajuste, el incremento para el mismo periodo fue de 4.5 por ciento.

Para los resultados a nivel entidad federativa, se presentan las tablas 4.1 y 4.2. La primera tiene información sobre los ingresos en valores absolutos y a precios del 2015; la segunda, información en términos de variaciones porcentuales con respecto al levantamiento del 2014.

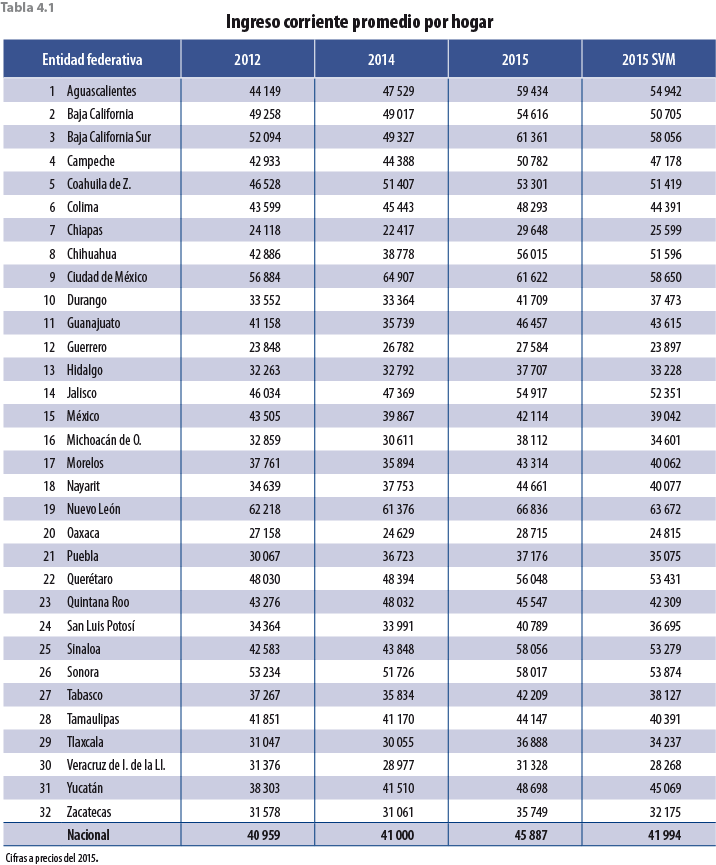
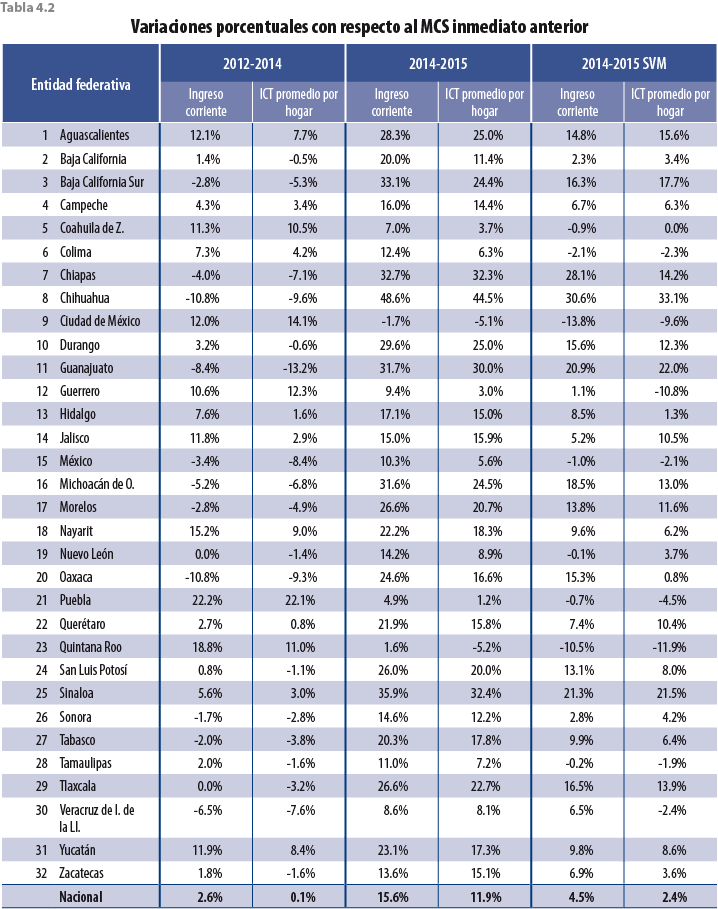
En la tabla 4.2 se puede observar que la tasa de variación tanto del ingreso corriente como del promedio por hogar para todas las entidades federativas disminuyó como consecuencia del ajuste a los factores de expansión.

En términos de fuentes de ingreso, la tabla 4.3 muestra sus variaciones porcentuales entre el 2014 y 2015; este último año considerando el ajuste propuesto.

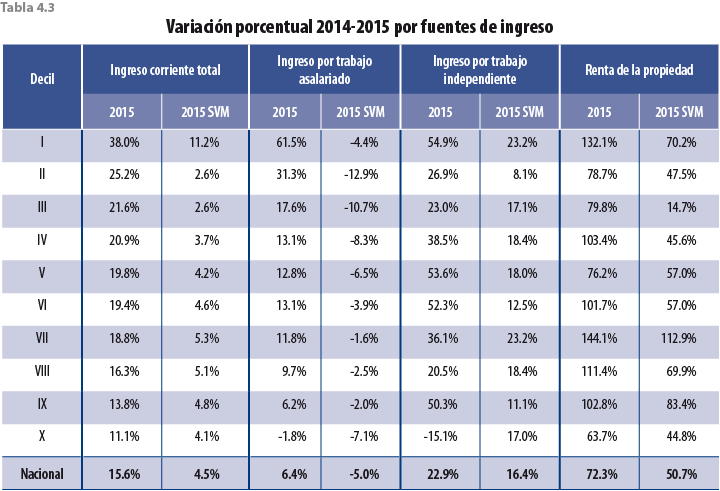
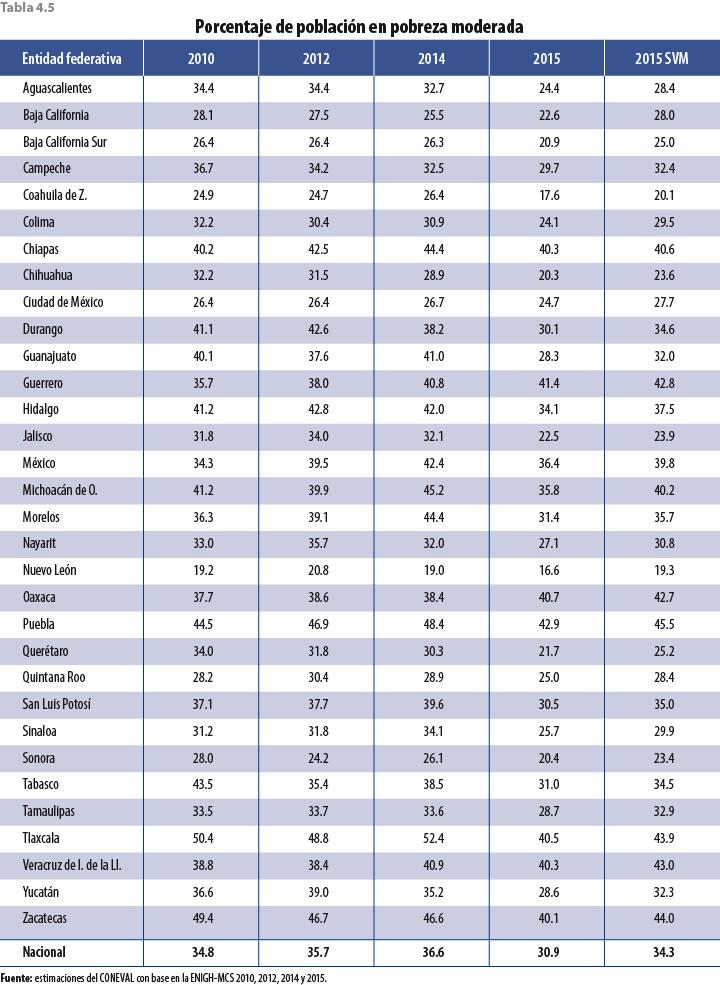
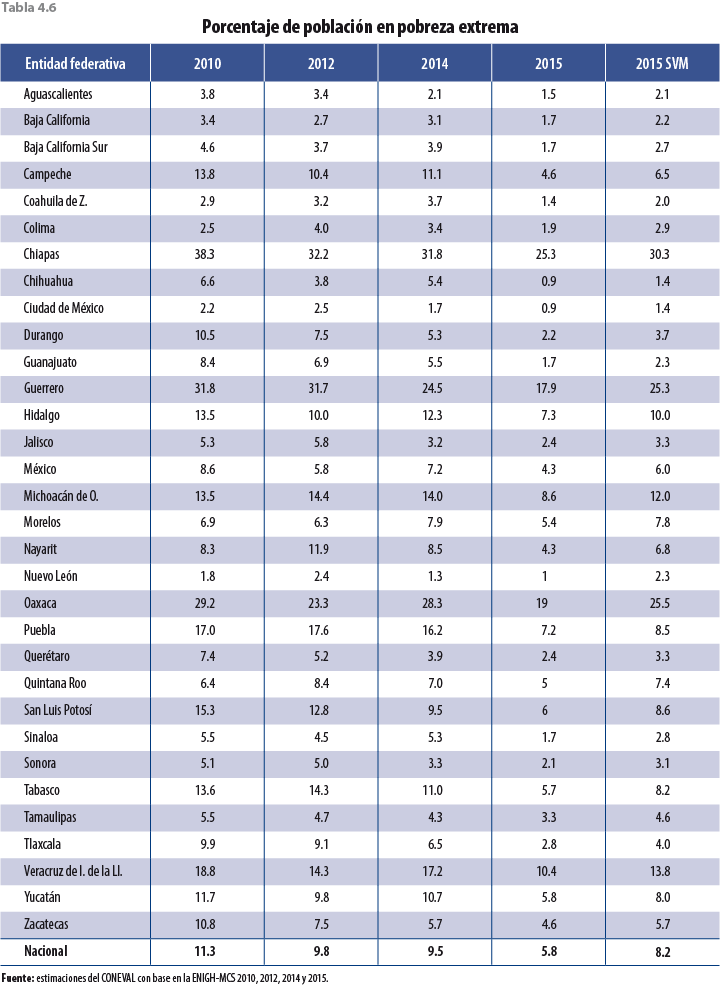
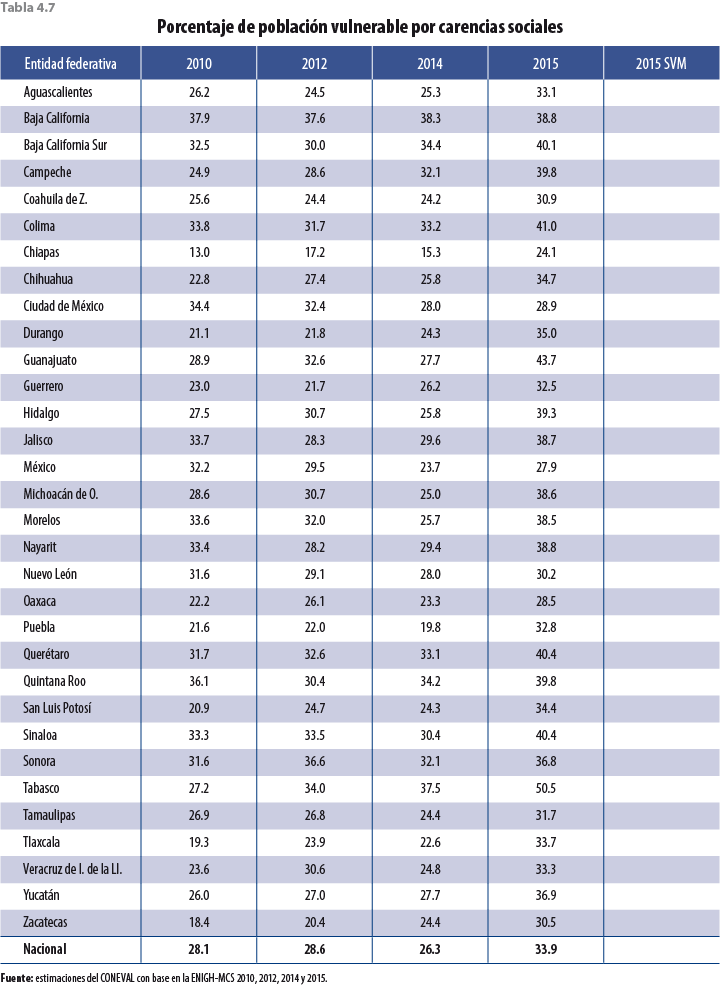
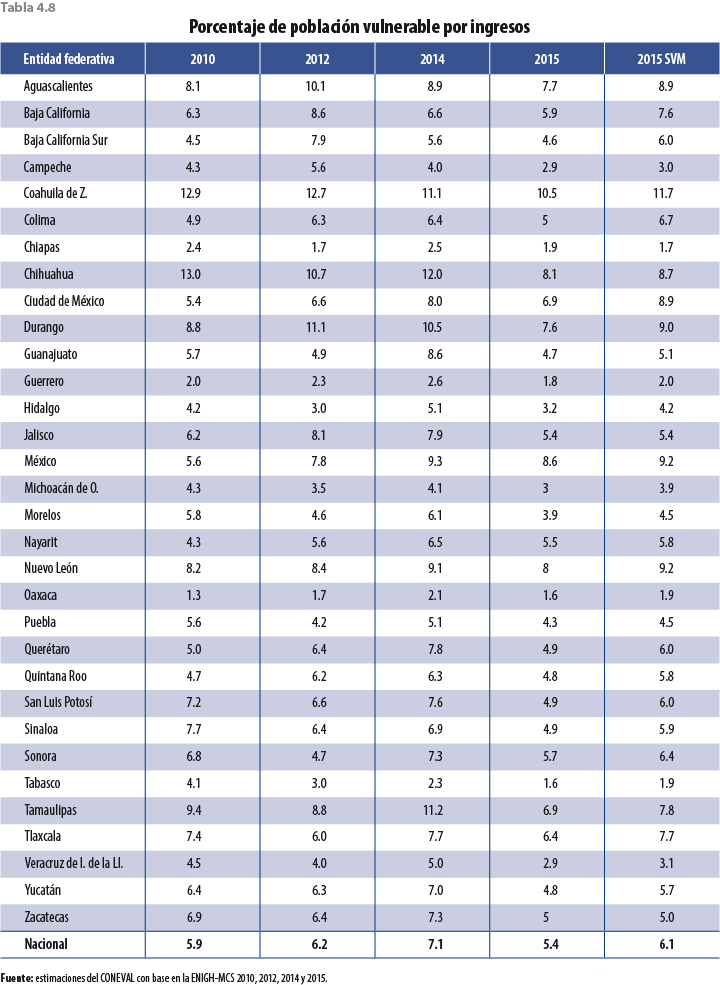
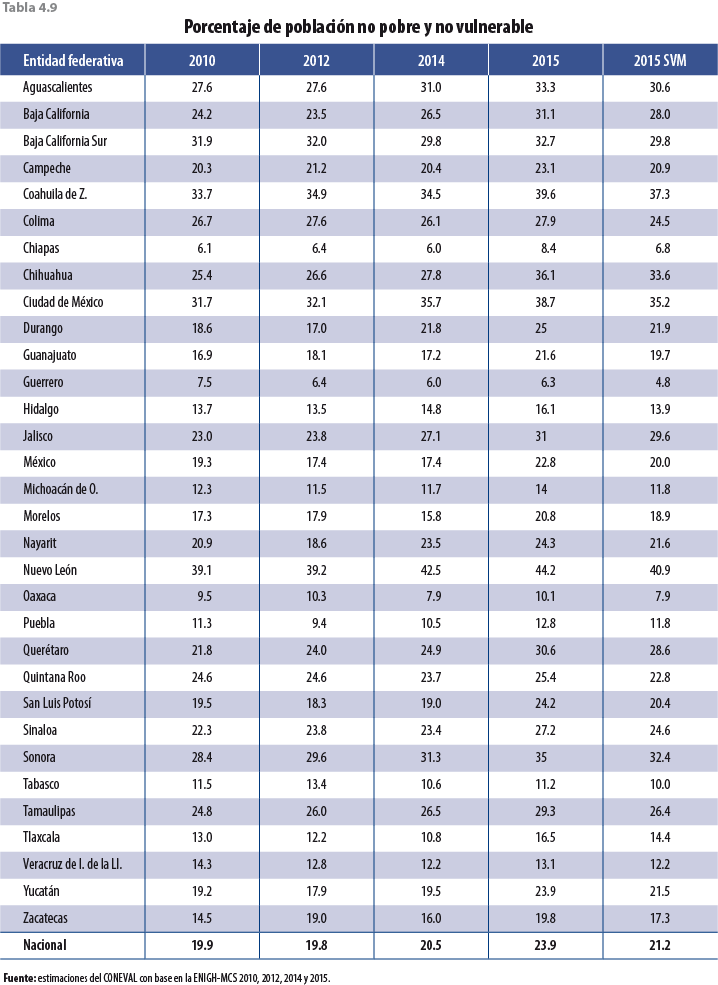
Si bien los ajustes en las tasas de crecimiento de las variables monetarias son a la baja, faltaría verificar si esta propuesta tiene el efecto esperado en pobreza; es decir, un aumento con respecto al MCS 2015 y un alineamiento con los años anteriores; para ello se presenta una serie de tablas a nivel entidad federativa con los distintos tipos de pobreza calculados por el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL), los cuales ya incorporan el ajuste correspondiente en el 2015.

La tabla 4.4 muestra los resultados de pobreza para cada uno de los estados y para el país. Debido a que esta metodología considera datos no solo del 2014 sino que también incorpora información anterior de entidades federativas, el comportamiento de los nuevos resultados de pobreza (aquellos resultantes de ajustar factores de expansión, con la técnica descrita en apartados anteriores) es más parecido al 2010 y el 2012 que al 2014.

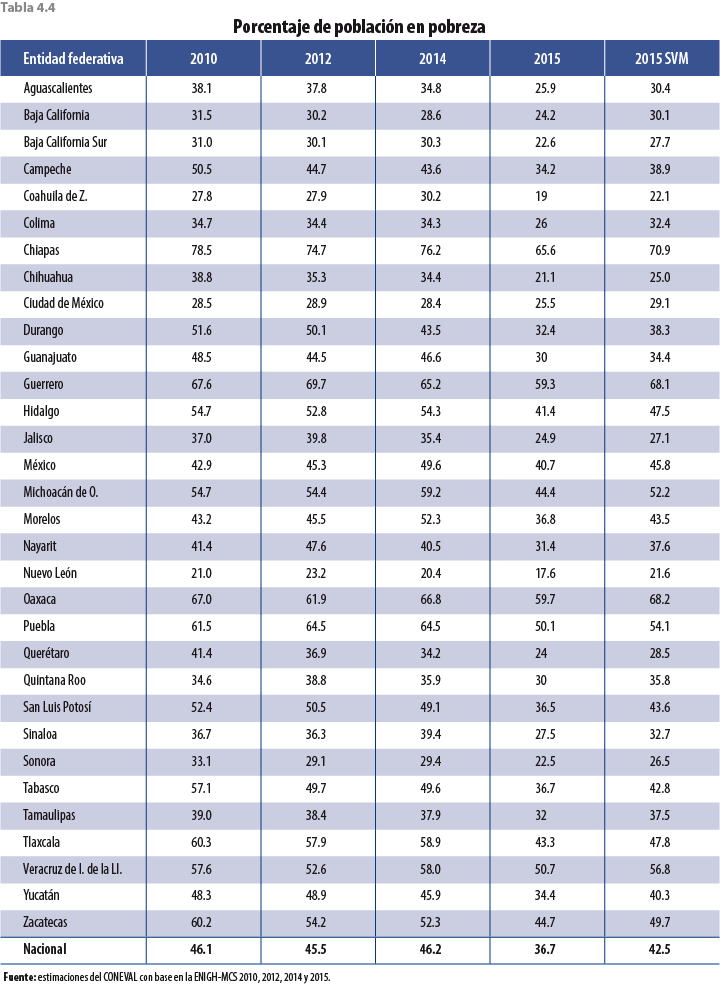
5. Validación y evaluación de la metodología

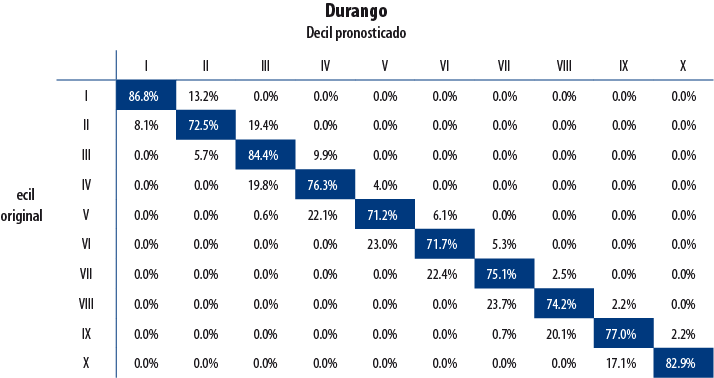
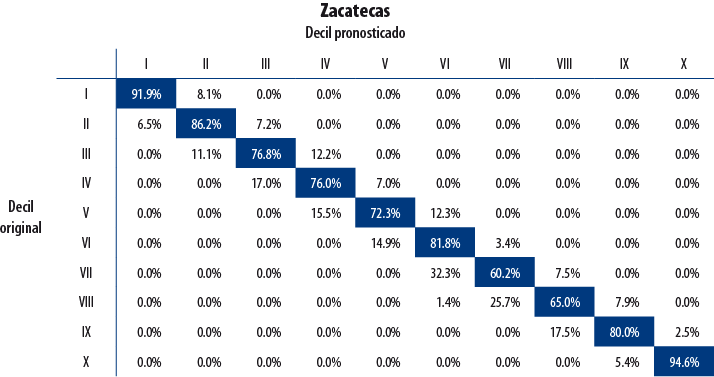
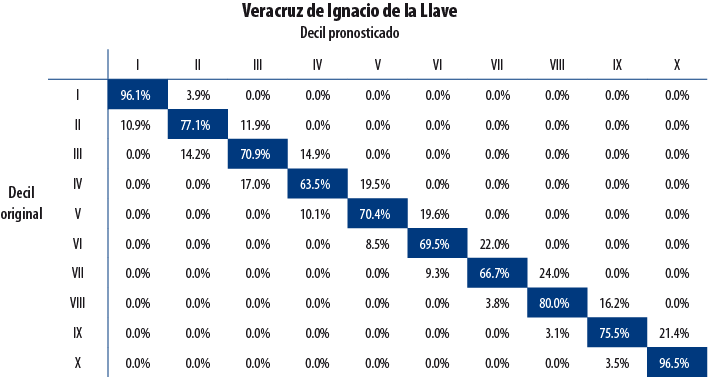
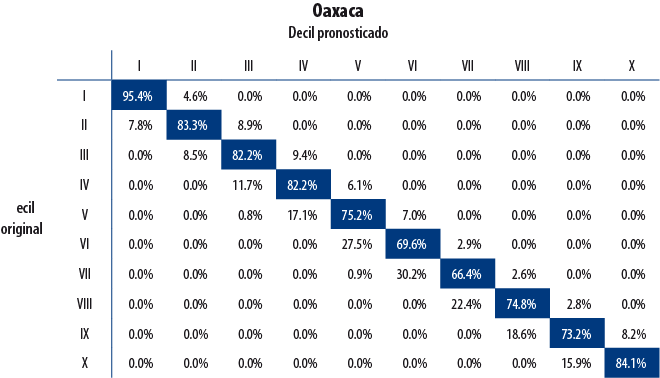
Una de las ventajas que tiene la metodología desarrollada en el apartado 3 consiste en que puede ser fácilmente evaluada con otras bases de datos. El mecanismo de validación comprende la información de los MCS 2010 y 2012 como datos de entrenamiento; como datos de prueba se usaron los del MCS 2014.

A continuación, se presentan los resultados de validación para cuatro entidades seleccionadas de forma aleatoria. La diagonal principal indica el porcentaje de hogares para quienes la decilización artificial y la original coincidieron; es decir, que la clasificación artificial no cambió el decil de pertenencia del hogar. Como se observa, el porcentaje de hogares para los cuales la clasificación resultó acertada es elevado.

6. Conclusión y comentarios finales

Como consecuencia de las mejoras realizadas en el levantamiento del MCS 2015 se observa un corrimiento del ingreso reportado por los hogares, rompiendo la continuidad con levantamientos del MCS-ENIGH anteriores; sin embargo, ello no implica que la información recabada por el INEGI sea errónea o sesgada.

Una manifestación del corrimiento del vector de ingreso se da al comparar resultados por deciles del MCS 2015 con deciles del MCS 2014: las tasas de crecimiento del 2014 al 2015 del ingreso corriente total de cada decil fueron muy superiores a las que se venían observando.

La metodología que aquí se propone para recomponer la continuidad del MCS 2015 con los años anteriores consiste en la modificación de los factores de expansión, dejando inalterada la declaración de ingresos por parte de los hogares.

La forma de lograr continuidad consiste en modificar la representatividad que tiene un hogar de acuerdo con su asignación a un decil pronosticado o artificial, creado para ese propósito a partir de un conjunto de variables monetarias y no-monetarias. La asignación de un hogar a un decil pronosticado se realiza a través de una técnica de Machine Learning, conocida como máquina de soporte vectorial; esta técnica consiste en entrenar una máquina con datos de MCS anteriores al 2015 con el fin de pronosticar el decil de pertenencia de un hogar en el 2015. Para hacer comparaciones válidas con los resultados de los MCS anteriores, el supuesto en el que se basa la propuesta es que los hogares que pertenecen a determinado decil, considerando sus nuevos factores de expansión, representan a aquellos hogares que bajo circunstancias similares a las históricas hubiesen pertenecido a ese decil.

Una ventaja de este método es que utiliza información histórica para hacer pronósticos en el 2015 sin modificar la información reportada por los hogares, además de que trata de minimizar las clasificaciones erróneas y sus resultados son fácilmente validables y comparables. Sin embargo, debe considerarse que al ser una técnica de optimización, los resultados dependerán de las covariables incluidas y de los parámetros de ajuste especificados dentro del paquete computacional, aunados a las posibles consecuencias en el diseño muestral a causa de la modificación de los factores de expansión.

En términos de resultados, la variación porcentual entre el 2014 y 2015 del ICT a nivel nacional pasó de 15.6 a 4.5% con la presente propuesta de ajuste. Respecto a la variación porcentual en el decil I, ésta pasó de 38 a 11.2%; mientras que en el decil X fue de 11.1 a 4.1 por ciento. En términos de medición de pobreza, el porcentaje de población en pobreza según el MCS 2015 fue de 36.7, en tanto que con el ajuste aumentó a 42.5 por ciento. La pobreza extrema creció de 5.8 a 8.2%, mientras que la moderada fue de 30.9 a 34.3 por ciento.

_____

Fuentes

Cortes, Corina y Vladimir Vapnik. “Support vector networks”, en: Machine Learning. Boston, United States of America, Kluwer Academic Publishers, 1995.

Hastie, Trevor; Robert Tibshirani y Jerome Friedman. The Elements of Statistical Learning. Data Mining, Inference, and Prediction. New York, United States of America, Springer, 2009.

Schölkopf, Bernhard y Alexander J. Smola. Learning with kernels: Support vector machines, regularization, optimization, and beyond. Cambridge, England, MA, MIT Press, 2002.

Witten, Ian y Eibe Frank. Data Mining: Practical Machine Learning Tools and Techniques. San Francisco, CA, United States of America, Morgan Kaufmann, 2011.

7. Anexo
_____

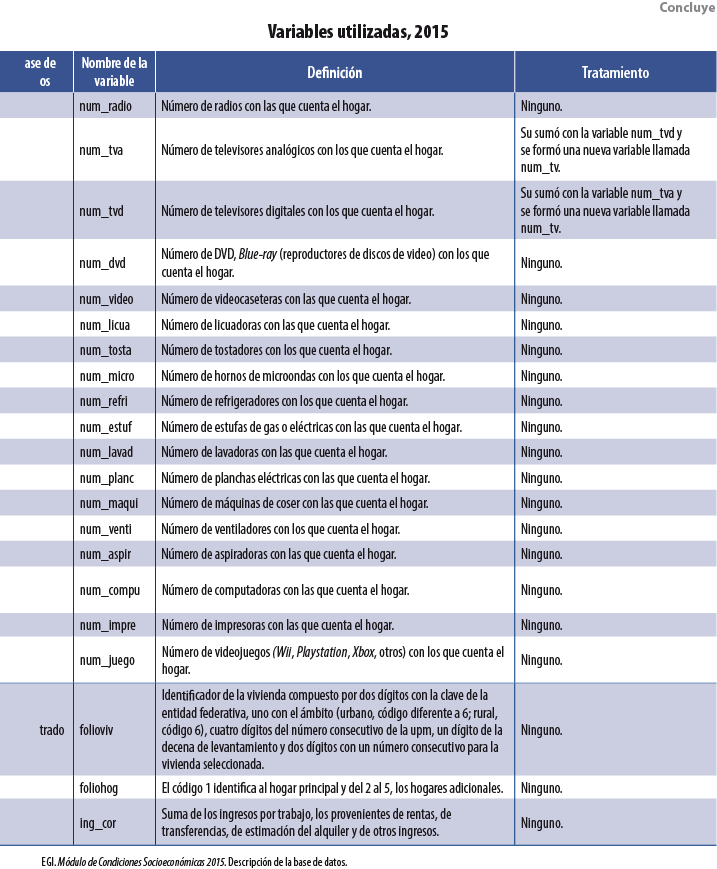¹ El presente apartado es un extracto del capítulo 12 del libro The Elements of Statistical Learning. Data Mining. Inference and Prediction. Para mayor detalle, se recomienda consultarlo directamente.

² Las variables monetarias se encuentran en pesos del 2015

³ Entre las técnicas probadas se encuentran redes neuronales, árboles de decisión y regresión logística multinomial.