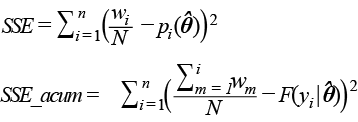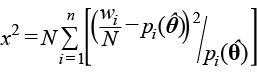Modelo estadístico 2016 para la continuidad del MCS-ENIGH

 

2016 Statistical Model for MCS-ENIGH’s Continuity

 

José Alejandro Ruiz Sánchez y Ana Miriam Romo Anaya
INEGI jose.ruizs@inegi.org.mx y miriam.romo@inegi.org.mx , respectivamente. 

Nota: los autores agradecen la colaboración de Lorenzo Cecilio Fernández en el proceso de integración del artículo.

 

Vol. 9 número especia – Epub                             Modelo estadístico 2016… – Epub

En un proceso de mejora continua, el Instituto Nacional de Estadística y Geografía (INEGI) identificó áreas de oportunidad en el Módulo de Condiciones Socioeconómicas (MCS) de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH), que se materializaron en la implementación de acciones operativas en la ENIGH 2016, con el objetivo de alcanzar un mayor apego al diseño de la encuesta. Con ello, se inicia una nueva serie de la ENIGH. Para dar continuidad a los resultados bienales de la serie del MCS-ENIGH, se propone una metodología de edición de microdatos basada en el ajuste de una función de distribución bajo restricciones. En una primera etapa, solo se modifican los ingresos por trabajo principal reportados en la ENIGH 2016; el ajuste se realiza en función de las tasas de crecimiento observadas en la Encuesta Nacional de Ocupación y Empleo (ENOE) por entidad federativa. En la fase siguiente, se modifica el resto del ingreso total de los hogares; para ello, nos basamos en una relación constante que se ha observado desde el 2010 entre los ingresos totales y los ingresos por trabajo principal. Como resultado de la modificación de los ingresos reportados, el crecimiento del ingreso total de los hogares entre el 2014 y los datos que arroja el modelo para el 2016 es de 2.1% (en comparación con 10.4%, si se utilizan datos de la ENIGH 2016). La variación para el primer decil es de 8.5% (mientras que con datos de la ENIGH 2016 fue de 29.9%).                                                                                                    Palabras clave: MCS-ENIGH; ENIGH 2016; imputación.

As a way to keep improving, INEGI identified some opportunity areas in the MCS-ENIGH, which resulted in the implementation of certain operative actions in the ENIGH 2016. This was aimed to get as close as possible to the survey’s design. This is the start of a new ENIGH series. We propose a new micro-data editing methodology in order to keep the continuous biennial results of the MCS-ENIGH series. This methodology is based on the adjustment of restricted distribution functions. On a first stage, only incomes per main labor reported in ENIGH 2016 are modified, with the adjustment done according to the growth rates observed in ENOE by Federal entity. In the next stage, we modified the rest of households’ total income based on a constant relation observed since 2010 between total incomes and incomes derived from a person’s main labor. As a result of the modifications of reported incomes, households’ total income growth, between 2014 and the data we get from the model designed for 2016, is of 2.1% (unlike the 10.4% we get when compared to data from ENIGH 2016 without adjustments). The variation for the first decile is of 8.5% (it was of 29.9% with data from ENIGH 2016 without adjustments).                                                                                                                                                                                                     Key words: MCS-ENIGH; ENIGH 2016; imputation.

 

1. Introducción

En un proceso continuo de mejora, el INEGI identificó áreas de oportunidad alrededor de la capacitación, supervisión y control operativo del Módulo de Condiciones Socioeconómicas de la Encuesta Nacional de Ingresos y Gastos de los Hogares (MCSENIGH). A partir de ello, se llevaron a cabo acciones de fortalecimiento operativo en el levantamiento de la ENIGH 2016 en un esfuerzo por alcanzar un mayor apego al diseño de la encuesta.

Con estas medidas implementadas, se inicia una nueva serie histórica para las encuestas de ingresos y gastos de los hogares. Sin embargo, y partiendo del reconocimiento de la necesidad de preservar la continuidad de sus ejercicios estadísticos, se presenta esta propuesta metodológica, cuyo objetivo es proveer de los insumos necesarios para la medición de la pobreza multidimensional, de tal manera que se mantenga la consistencia con los resultados de la serie bienal 2008-2014, tanto a nivel nacional como por entidad federativa.

En la medición de la pobreza multidimensional se incorporan variables no monetarias como la condición de acceso a salud, educación, seguridad social, etc., pero también otras que reflejan el ingreso de los hogares. Este documento está centrado solo en la modificación de este último grupo. En México, el encargado de medir la pobreza es el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL), cuya metodología toma como insumo la base de datos del MCS-ENIGH. Por lo tanto, una parte fundamental del proceso de ajuste consistirá en el desarrollo de un mecanismo que permita transitar de relaciones agregadas a nuevos microdatos de ingresos que sustituyan a los originalmente reportados.

El ingreso total de los hogares proviene de múltiples fuentes, por ejemplo: salarios, ganancias de empresas, recursos que reciben de otros hogares, etcétera. La ENIGH captura esa heterogeneidad a través de una serie de reactivos que son recabados a nivel individuo. La gran cantidad de preguntas referidas a los distintos canales de ingreso, entre otras características, hacen que la ENIGH tenga elementos que no poseen otros operativos similares levantados en el país.

A pesar de la diversidad de fuentes, la mayor parte del ingreso de los mexicanos proviene de su ingreso laboral, es decir, de su trabajo como asalariado y/o independiente (principal y secundario) que, en conjunto, ha representado cerca de 70% del ingreso corriente total (ICT) desde el 2010. Este elevado porcentaje, junto con la existencia de un levantamiento regular sobre condiciones laborales, como lo es la Encuesta Nacional de Ocupación y Empleo (ENOE), crean una ventana de oportunidad para utilizar el ingreso laboral que reporta esta encuesta como ancla para ajustar los ingresos laborales.¹

Para la modificación de los ingresos laborales reportados por los hogares, aproximamos una función de densidad de probabilidad a los datos empíricos del ingreso de la ENIGH 2016; posteriormente, se ajusta otra función de densidad pero ahora imponiéndole como condición que sea capaz de generar nuevos microdatos tales que arrojen un valor objetivo de un estadístico específico (por ejemplo, un determinado promedio muestral); en nuestro caso, ese valor proviene de la trayectoria para cada entidad federativa de los ingresos laborales de la ENOE.

Al modificar solo el ingreso laboral, la relación entre éste y el ingreso no laboral se ve alterada, rompiendo una trayectoria histórica que se venía observando desde el 2010. Para recomponer la relación, y en una segunda fase, se modifica el ingreso no laboral, de tal forma que se elimine el efecto colateral causado por el primer ajuste. Así, esta metodología modifica solo las variables de ingreso, dejando inalteradas las variables no-ingreso y los factores de expansión; esto último permite mantener el diseño muestral de la ENIGH.

El documento se encuentra dividido en siete secciones. En la segunda se presentan algunos estadísticos descriptivos que permiten conocer la magnitud y distribución de los efectos de las mejoras. En la tercera se desarrolla el marco teórico general de la metodología para modificar microdatos. En la siguiente se crean nuevos microdatos del ingreso por trabajo principal (ITP). En la quinta se presenta la segunda y última fase del ajuste a los ingresos de los hogares, relacionada con la modificación de los ingresos distintos al ITP (ITP^c ). En la penúltima se muestran los principales resultados del ajuste y en la última, se concluye.

2. Análisis descriptivo

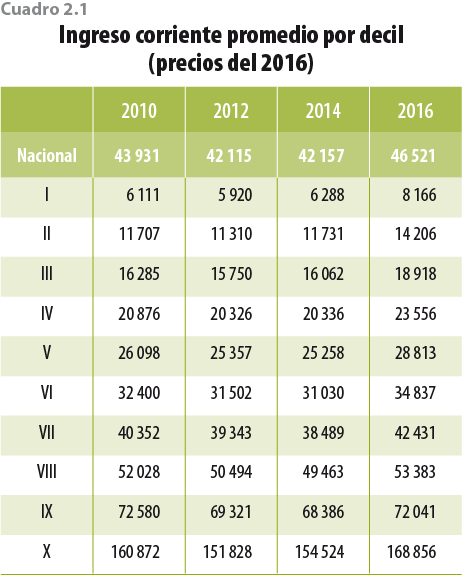
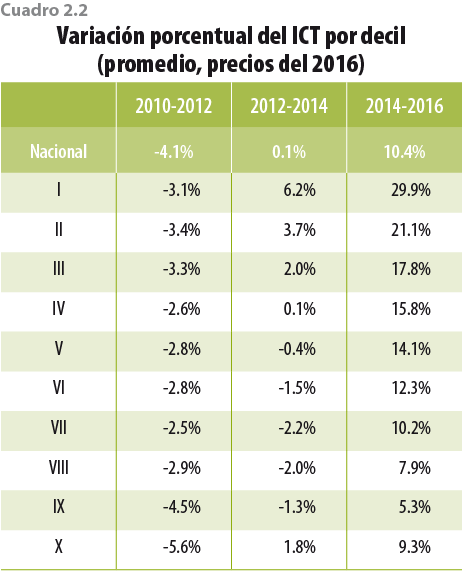
Como consecuencia de las acciones tomadas, el ICT que reportan los hogares en la ENIGH 2016 tiene incrementos sustanciales con respecto al 2014, en especial para los primeros deciles (ver cuadros 2.1 y 2.2).² Lo anterior se debe, en parte, a que ahora el problema de la subdeclaración que hacen los hogares es menor; ello se ve reflejado en el porcentaje que indicó recibir menos de 3 mil pesos trimestrales, el cual pasó de 0.7% en el 2014 a 0.2% en el 2016 a nivel nacional (ver figura 2.1).
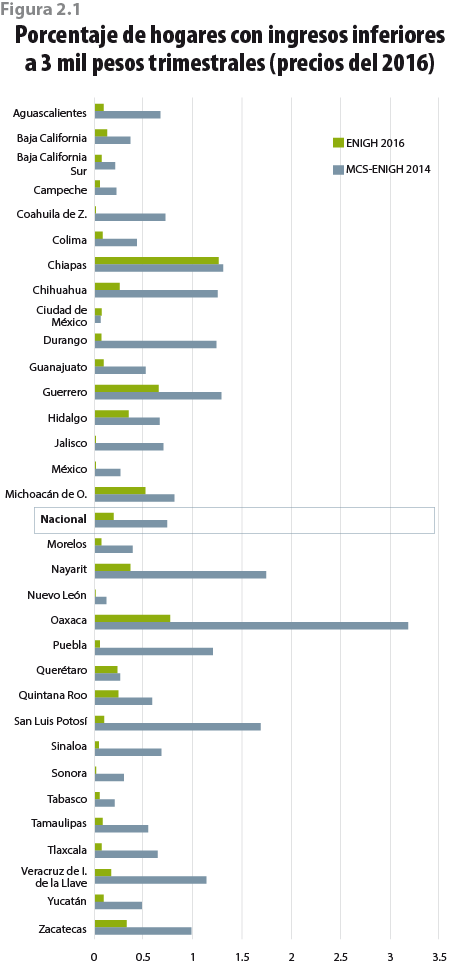A nivel entidad federativa, los porcentajes muestran la misma tendencia decreciente (excepto en la Ciudad de México); incluso, para algunas entidades como Coahuila de Zaragoza, Jalisco, México, Nuevo León y Sonora, el porcentaje es cercano a cero.

Los cambios en tendencia mostrados en los cuadros anteriores son el resultado de las mejoras implementadas en el 2016, por lo que la información de la ENIGH 2016 no es consistente con la de años anteriores.

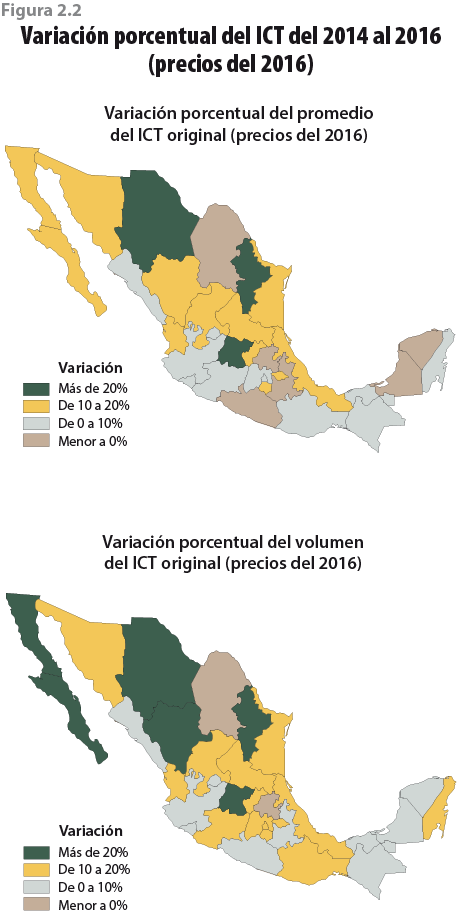
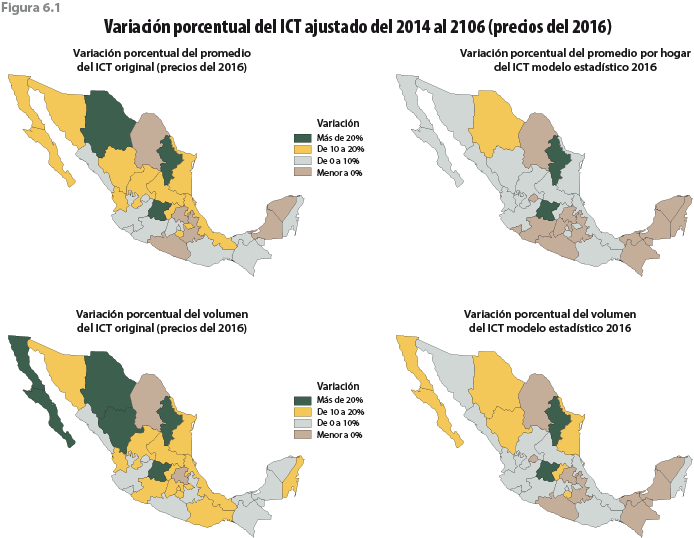
Por otra parte, y debido a que las instrucciones para una mejor recolección de la información se dieron a nivel nacional, la declaración de ingresos tuvo un efecto en las distintas entidades federativas, aunque de manera diferenciada. La figura 2.2 permite identificar regiones de acuerdo con su variación porcentual en el ingreso por hogar entre el 2014 y 2016. Observamos que, tanto en volumen como en promedio, la zona norte del país fue la que experimentó las mayores variaciones con respecto al 2014, llegando a niveles superiores a 20% en entidades como Nuevo León y Chihuahua.
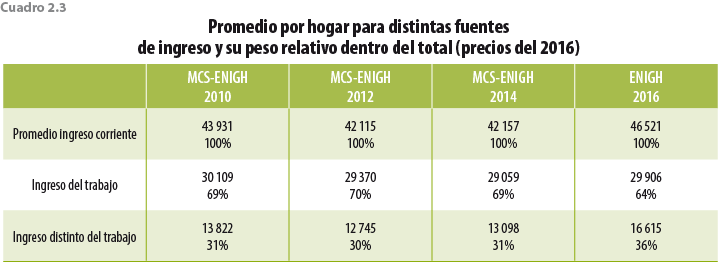
Otro nivel de desagregación que se puede lograr con la información de la ENIGH es por fuentes de ingreso, es decir, aquellos rubros que componen el ingreso total de los hogares. Es deseable analizar el comportamiento con esta división ya que nos permite identificar y relativizar los cambios más sustanciales dependiendo de la procedencia de los ingresos. El cuadro 2.3 contiene el promedio nacional de cada una de las principales fuentes de ingreso, así como el peso que tienen con respecto al ingreso corriente total. Si bien el ingreso del trabajo no tuvo los incrementos de otras fuentes de ingreso, su peso dentro del ICT hace que sea un componente fundamental para recuperar la trayectoria histórica. Históricamente, la fuente de mayor importancia dentro del ICT son los ingresos del trabajo (principal y secundario), este componente ha representado poco menos de 70% del total.
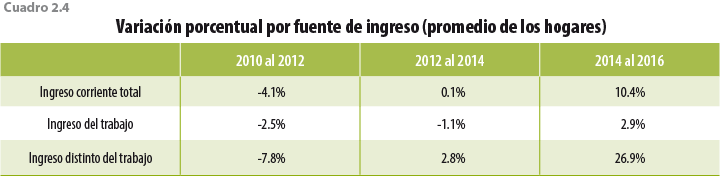
Un aspecto a resaltar es que el comportamiento de estas dos fuentes de ingreso es distinto: los derivados por trabajo crecieron 2.9% entre el 2014 y 2016, mientras que el restante creció 26.9% en el mismo periodo (ver cuadro 2.4).
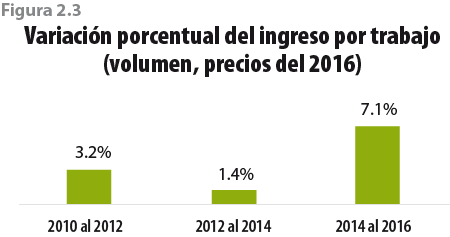
En términos del monto total de los ingresos por trabajo, la mayor variación porcentual con respecto al levantamiento previo se observó entre el 2014 y 2016 cuando aumentó 7.1% (a precios del 2016) (ver figura 2.3). Ello, en combinación con el cuadro 2.4, implica que el número de personas con ingresos laborales también tuvo un crecimiento sustancial.
Por otra parte, la gran diversidad de fuentes de ingresos captadas en la ENIGH no permite tener una contraparte para cada una de ellas, ya sea en encuestas o en agregados económicos; sin embargo, sí existe un levantamiento paralelo para el ingreso por trabajo: la ENOE; ésta, al igual que el MCS-ENIGH, tiene representatividad tanto a nivel nacional como por entidad federativa y ambas comparten el mismo marco muestral. La ENOE se levanta desde el 2005 con una periodicidad trimestral, cuya muestra rotatoria es de más de 120 mil viviendas; cada trimestre se sustituye 20% de las viviendas y cada vivienda es entrevistada durante cinco ocasiones antes de ser reemplazada; esto permite que en cada trimestre se mantenga 80% de la muestra. Otra ventaja de la ENOE es que no fue objeto de las mejoras implementadas en la ENIGH 2016. El objetivo de la ENOE es obtener información sobre las características ocupacionales de la población, por lo que no obtiene información de todas las fuentes de ingresos de los hogares. Un problema bien identificado en la ENOE es el elevado número de personas que no reportan ingresos; el porcentaje es cercano a 60% del total de individuos a los cuales se les aplicó el Cuestionario de ocupación y empleo, en distintos levantamientos desde el 2010 a la fecha. Para aminorar esta situación, el cuestionario agrega un reactivo de rescate que pregunta por un rango salarial a aquellas personas que, aun cuando se les preguntó el monto de sus ingresos, no contestaron un ingreso puntual. Para incorporar las respuestas por rangos salariales, se tienen diferentes opciones, la que usamos en esta metodología es la misma que propone el CONEVAL en la construcción del índice de la tendencia laboral de la pobreza y que se encuentra detallada en el anexo del documento publicado en internet (bit.ly/3Y6SeZK).

La información que reporta el MCS-ENIGH sobre los ingresos de los hogares es de hasta seis meses anteriores a la fecha del levantamiento y, debido a que la obtención de la información es de agosto a noviembre, el periodo reportado en la encuesta es de febrero a octubre (de estos nueve meses, cada hogar solo reporta seis, dependiendo del mes en el que es encuestado). Por otra parte, y dado que la realización de la ENOE es trimestral, aquellos periodos donde hay mayor coincidencia con la información del MCSENIGH son el segundo y el tercer trimestre; es por ello que, para los datos obtenidos de la ENOE, consideramos dichos periodos. La desventaja que esto conlleva es que en esos trimestres solo se recoge información del trabajo principal y se excluye lo correspondiente al secundario.

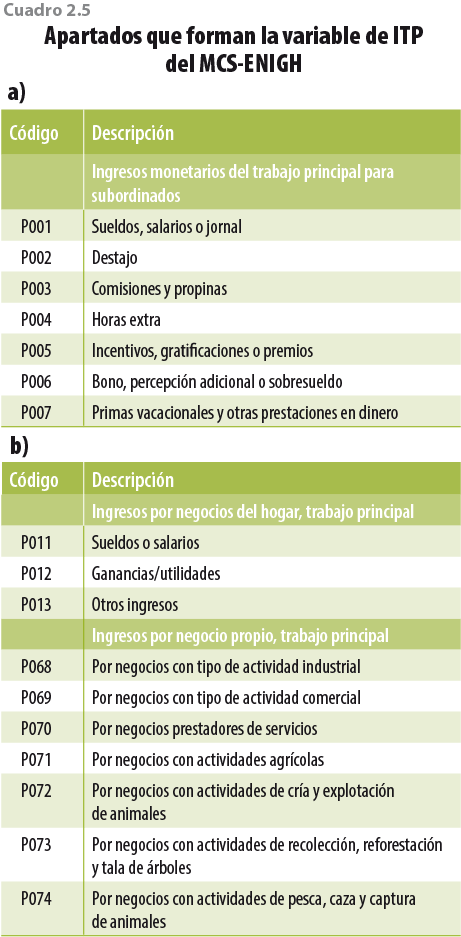
Como consecuencia de lo anterior, debemos identificar los ingresos obtenidos por el trabajo principal dentro del MCS-ENIGH y la ENIGH 2016 para hacerlos comparables con los de la ENOE. El MCSENIGH y la ENIGH 2016 generan información a nivel individuo y por tipo de ingreso recibido; este ingreso se encuentra clasificado por códigos y se pueden consultar en el documento metodológico de la encuesta. Los codigos que utilizaremos para generar la variable de ITP son los que se muestran en el cuadro 2.5 que, para fines prácticos, se pueden agrupar en ingresos por trabajo subordinado (columna a) y por trabajo independiente (columna b).
Para terminar de formar la variable ITP, tanto en el MCS-ENIGH como en la ENIGH 2016 y en la ENOE, sumamos los ingresos a nivel hogar. Para la ENOE se mantienen solo aquellos hogares en los que todos sus integrantes declaran algún ingreso (incluso si esa declaración es cero).

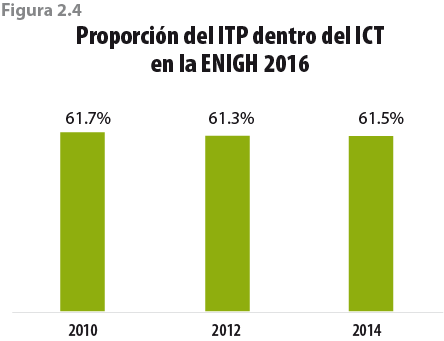
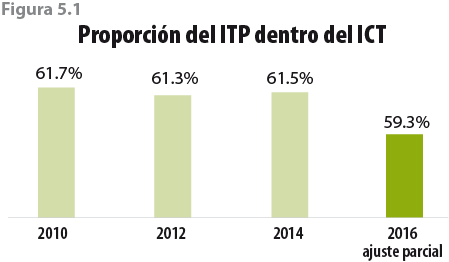
Como proporción del ICT, el ITP ha sido relativamente estable (61.5% en promedio) durante el periodo del 2010 al 2014, tal como se muestra en la figura 2.4. Dicha estabilidad será importante en nuestra metodología, como se explicará más adelante.
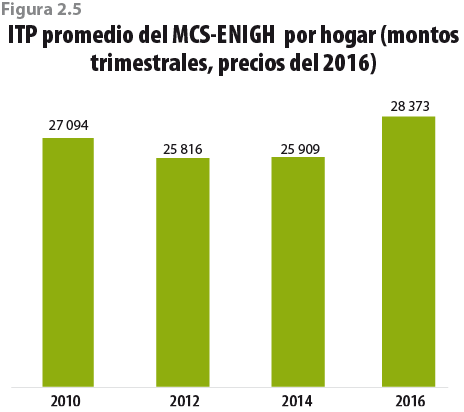
La figura 2.5 muestra el promedio nacional del ITP: en ella se observa una caída entre el 2010 y 2012 de más de 1 200 pesos; también se aprecia que el cambio más importante se dio entre el 2014 y 2016, con un crecimiento superior a los 2 000 pesos.
A grandes rasgos, la metodología usa la tasa de crecimiento del ITP_ENOE (ingreso por trabajo principal de la ENOE) dentro de cada entidad federativa, para ajustar el valor del ITP_ENIGH (ingreso por trabajo principal de la ENIGH) reportado por los hogares. Sin embargo, al ajustar solo el ITP, la proporción entre éste y el ICT se verá alterada. Si suponemos que esa relación debe ser similar a la observada históricamente (ver figura 2.4), ello nos permitiría tener un contrafactual para modificar el complemento del ITP (ITP^c ). Así, el ajuste al ICT sería en dos fases: en la primera se modifica el ITP con base en el comportamiento de la ENOE, y en la segunda se modifica el ITPc con base en el peso que a través del tiempo ha tenido el ITP dentro del ICT. En las siguientes secciones se detalla el proceso.

3. Metodología

La metodología toma como marco teórico el trabajo desarrollado por Bustos (2015). En su artículo, el autor propone que, además de aproximar una función de distribución a los datos que arrojan encuestas como la ENIGH, se tomen datos puntuales de fuentes como las cuentas nacionales para imponerlos como restricciones al ajuste de la distribución teórica y, así, corregir problemas como el de la subdeclaración. De esta forma, se tendrían estimaciones más cercanas a la realidad sobre la distribución del ingreso de los hogares.

Comencemos suponiendo que la variable de interés se puede modelar a través de una función de densidad de probabilidad paramétrica. Es decir, si dicha variable la denotamos como y, entonces f(y; θ)es la función de densidad asociada a su función de distribución F(y|θ) . Los valores del vector de parámetros θ = (θ₁, θ₂,…, θ_k) son desconocidos y deben estimarse procurando errores mínimos de medición, de tal manera que se pueda reconstruir lo mejor posible la distribución empírica (aquella obtenida a partir de datos recopilados por medio de una encuesta, por ejemplo).

Recordemos que una función de distribución acumulada teórica representa las probabilidades acumuladas obtenidas de la función de densidad. Es denotada por F_Y (y|θ) y se interpreta como la probabilidad de que la variable Y asuma un valor menor o igual a y. Se define como:

(1)

Así, para un cierto intervalo de ingresos [a, b], tenemos que:

(2)

Debido a que la función F(y|θ) es estrictamente creciente, entonces existe su inversa, la cual es llamada función cuantil. Ésta es la que usaremos para obtener los microdatos estimados.

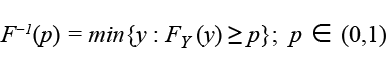(3)

Por otro lado, la distribución acumulada empírica es la frecuencia acumulada de los datos observados ordenados de forma ascendente; en nuestro caso, y como los datos provienen de un diseño de muestreo, usamos los factores de expansión para definir dicha frecuencia como la proporción de elementos (hogares) observados que tienen un valor menor o igual a un valor observado y. Se representan por la siguiente expresión:

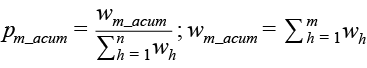
para cada m = 1,2,…,n;

donde w_h es el factor de expansión asociado al hogar h y n es el número total de hogares en la muestra.

Ahora bien, una vez elegida la forma funcional paramétrica f(y; θ) lo siguiente es establecer el método de optimización que se usará para encontrar el estimador del vector de parámetros θ. Existen diversos métodos que cumplen con esta finalidad; entre los más comunes se encuentran el de momentos, el de mínimos cuadrados y el de máxima verosimilitud. Decidimos usar este último ya que, además de arrojar estimaciones con propiedades de eficiencia cuando se cumplen ciertas condiciones, hace máxima la probabilidad de que el modelo —dado por f(y; θ) — genere la muestra que se observó; también, ya hay un gran avance en la implementación computacional del algoritmo que resuelven de manera eficiente sistemas de ecuaciones no lineales.

El método consiste en tomar los n datos muestrales de la variable de interés, representada por el vector Y = (y₁, y₂,…, y_n), y suponer que esta variable tiene una función de distribución asociada f(y|θ) ; el estimador de θ (el de máxima verosimilitud) se obtiene calculando el máximo3 de la función pseudo-log-verosimilitud para datos con pesos (Skinner et al., 1989) denotada por l(θ) y definida como:

(5)

donde w_h corresponde al peso de la observación (hogar) h, con h = 1,…,n.

El valor de θ que maximiza la función anterior es llamado estimador de θ y lo denotaremos por θ_SR (el subíndice hace referencia a que es el estimador de un ajuste sin restricciones).

Con respecto al modelo de ajuste con restricciones, éste puede ser expresado de la siguiente manera:

(6)

Sujeta a:

siempre y cuando p < número de parámetros a estimar.⁴ c_i, d_i son constantes (valores objetivos).

De manera iterativa se encuentra el valor de θ que arroje un valor máximo de l(θ) y que cumpla con las restricciones impuestas. Es éste al que consideramos el mejor estimador y lo denotaremos como .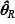

Las funciones H_i (.), I_i (.), pueden estar en términos de la variable de interés y/o de los valores del vector-parámetro θ. Así, por ejemplo, si la intención es que la variable Y en un cierto rango [0, c] tenga una probabilidad no mayor que c₁ , entonces, una de las restricciones tomaría la siguiente forma:

Si el objetivo es que la distribución teórica que ajusta a Y tenga una esperanza (promedio) igual a c₂ , entonces, una forma de expresar la función de restricción es:

Por otro lado, es posible a través de la especificación del modelo con restricciones, modificar recursivamente los microdatos muestrales (es decir, los datos de la encuesta) hasta obtener de ellos valores deseados de un estadístico muestral; así, por ejemplo, si deseamos que los nuevos microdatos (junto con sus factores de expansión w_h ) tenga un promedio igual a c₃ , entonces la restricción de igualdad tendría la siguiente forma:

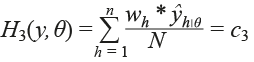
donde ŷ _h|θ es el nuevo valor para la observación h, dados los valores del parámetro θ (en la sección 3.1 se propone una forma de obtener ŷ _h|θ ).

Éstos son solo algunos ejemplos de la forma que pueden tener las funciones que definen las restricciones; pueden variar según sea el propósito del modelo y, como veremos enseguida, es factible que a través del modelo restringido se puedan editar los valores de los microdatos.

3.1 Generación de nuevos microdatos

Bajo el supuesto de que Y~f(y|θ) , y dados los estimadores 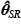y 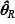, la forma de obtener los nuevos valores empíricos es la siguiente: se calcula la probabilidad acumulada, p_h= F(y_h| 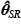) , que le correspondería al hogar muestral h de acuerdo con el valor y_h reportado; para ello, utilizamos la función de distribución acumulada teórica definida en (1). Una vez obtenida p_h para cada hogar de la muestra, nos olvidamos de la función de probabilidad sin restricciones y usamos la función inversa de la función acumulada con restricciones (determinada por el vector 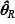); es decir, la función cuantil especificada en (3). Esta función toma un valor p_h y arroja un valor de ŷ_h , F^-1 (p_h| 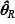) = ŷ_h ; de esta forma obtenemos, para cada hogar muestral, un nuevo valor de la variable y a través de una función de probabilidad con restricciones.

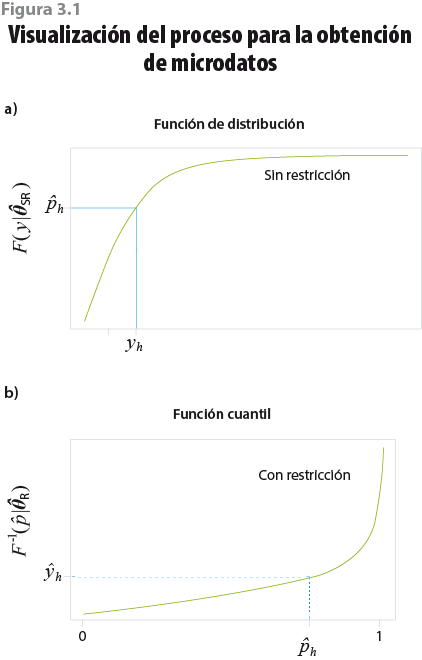
La figura 3.1 muestra de manera esquemática este proceso: la gráfica a) ejemplifica cómo a partir de un monto específico, y_h, se obtiene una probabilidad acumulada, 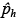, a través de la función acumulada sin restricciones; este proceso se repite para cada uno de los hogares de la muestra. Una vez fijadas las probabilidades acumuladas para cada hogar, y con ayuda de la función cuantil obtenida mediante el proceso de optimización con restricciones, se genera un nuevo valor ŷ_h, tal como se muestra en la gráfica b).
4. Ajuste al ingreso por trabajo principal

El ajuste al ingreso total de los hogares se realizará en dos etapas secuenciales, primero se modificarán los ingresos correspondientes al ITP y, después, los que forman el ICT, pero que son distintos al ITP (a los cuales llamamos complemento del ITP, ITP^c ).

Con base en la metodología desarrollada en el apartado anterior, en esta sección se detalla la modificación de microdatos relacionados con el ITP. El modelo requiere de un valor objetivo que debe alcanzar un estadístico deseado que, en nuestro caso, será la mediana del ICT de la ENIGH 2016. Para generar el valor objetivo que se debe alcanzar, se siguen estos pasos: en cada entidad federativa por separado se toman las medianas del ingreso reportado dentro del segundo y tercer trimestres de la ENOE para el 2014 y 2016. Con ellas se obtienen los promedios entre los dos trimestres del mismo año. Posteriormente, se calculan las variaciones porcentuales del promedio de las medianas del 2016 con respecto al del 2014. De esta manera, tenemos 32 tasas de crecimiento de las medianas entre el 2014 y 2016. Enseguida, y para cada entidad federativa, se calculan las medianas del ICT del MCS-ENIGH 2014; a éstas les aplicamos la tasa de crecimiento obtenida con los datos de la ENOE para, finalmente, obtener una mediana objetivo para cada entidad en el 2016 que denotaremos como Me = (Me1, Me2,…, Me32).

Una vez que hemos determinado tanto el estadístico deseado como su valor objetivo a alcanzar generamos nuevos valores del ICT para cada hogar, de acuerdo con la metodología de la sección anterior. Sin embargo, y para lograr ajustes diferenciados entre fuentes de ingreso, los valores originales del ICT y los nuevos valores son usados solo para modificar el ITP (como más adelante se explica), mientras que el ITP^c se modificará en función de la relación histórica entre el ITP y el ICT (ver figura 2.4).

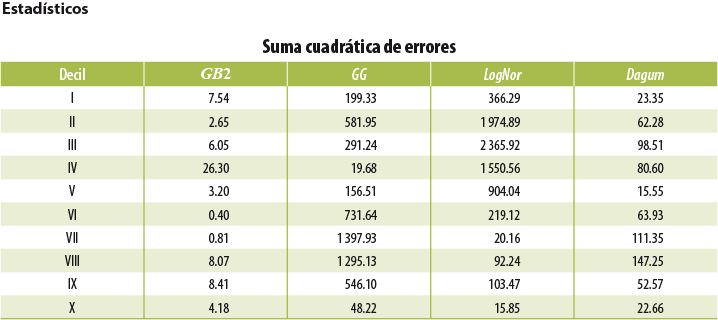
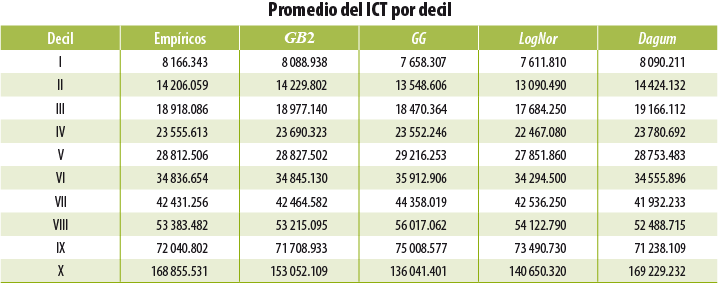
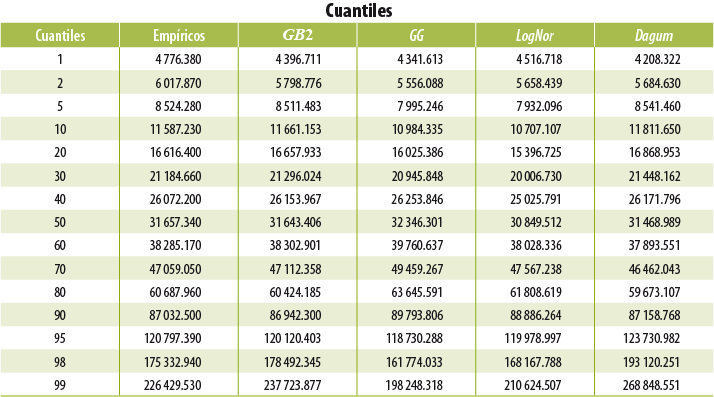
Una de las primeras tareas a resolver es la elección de la forma funcional que mejor se ajusta a los ingresos observados. En el Anexo 1 se especifican las formas funcionales de cuatro funciones paramétricas⁵ elegidas para ser sometidas a pruebas de ajuste: Gama Generalizada (GG), Beta Generalizada del segundo tipo (GB2), LogNormal (LN) y Dagum. En el Anexo 2 se incluyen los resultados de los estadísticos de ajuste a partir de los cuales elegimos la función de distribución con la que trabajaremos.

Con base en dichos criterios, se determinó que la GB2 con cuatro parámetros( µ, σ, υ, τ ) es la que mejor se ajusta a los ingresos reportados del ICT a nivel nacional.

Definida la función f(y|θ) = GB2(θ) = GB2 ( µ, σ, υ, τ ) el proceso formal para ajustar el ingreso ICT en cada entidad es como se expresa a continuación.

Sea Yⁱ = (yⁱ₁, yⁱ₂,…, yⁱ_n ) el vector de ingreso corriente total para la entidad i; sus pesos (factores de expansión) correspondientes están dados por wⁱ = (wⁱ₁, wⁱ₂,…, wⁱ_n ). Entonces, el ajuste de la distribución a los datos empíricos que corresponde a maximizar la log-verosimilitud de la GB2(θ) se expresa de la siguiente manera:

Para cada entidad i = 1,2,3,…,32

(7)

Resultado de estos ajustes obtendremos 32 estimadores de los parámetros de la distribución, los cuales representamos como donde .

Posterior al ajuste obtenido, se realiza un nuevo ajuste en el que incluimos como restricción que los nuevos microdatos generen la mediana objetivo para la entidad federativa correspondiente.

Es decir, sea Yⁱ_o = (yⁱ₍₁₎, yⁱ₍₂₎,…, yⁱ_(n)) el vector ordenado de ingresos para la entidad i y sus correspondientes pesos muestrales (factores de expansión) denotados por wⁱ_o = (wⁱ₍₁₎, wⁱ₍₂₎,…, wⁱ_(n)) ; y sea el vector de medianas objetivo Me = (Me₁, Me₂,…, Me₃₂); para cada entidad i = 1,2,3,…,32 se resuelve el siguiente problema de optimización restringida:

(8)

sujeto a:

a) Restricciones de igualdad:

donde:

yⁱ_(k) es el ingreso asociado al subíndice k tal que 0.5 ≤ w_(k) / w_(n) Lorem ipsum y 0.5 ≤ 1 – w_(k–1) / w_(n) con w_{( j)} = ∑^j_h = ₁wⁱ_(h)

Me_i es la mediana objetivo de la entidad federativa i.

θⁱ_SR es el estimador de los parámetros de la función teórica de densidad sin restricciones para la entidad i.

F(∙)es la función de probabilidad acumulada de GB2. F^-1 (∙)es la función cuantil de GB2 y

donde:

maxⁱ = yⁱ_(n) es el valor máximo del ingreso de ICT en la entidad i.

p^max (θⁱ_SR) = F(yⁱ_(n)| 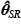) es la probabilidad acumulada (bajo la función teórica sin restricciones) correspondiente al valor max en la entidad i.

b) Restricciones de desigualdad: las propias del dominio de los valores de los parámetros de la función densidad, para GB2 (µ, σ, υ, τ):

La segunda restricción de igualdad tiene como objetivo controlar el carácter no finito en el dominio de las funciones de distribución. Para lograrlo, tomamos el valor más grande del ICT que se obtuvo en la encuesta en cada entidad federativa y establecemos que los nuevos ingresos estimados estén en [0, max ⁱ ].

Derivado de los modelos optimizados, obtenemos un vector que contiene los estimadores de los parámetros restringidos de la función GB2, que denotamos como , donde .

Lo siguiente es calcular los nuevos microdatos del ICT; para ello, y como se explicó en la sección 3, utilizamos tanto la función de distribución acumulada como la cuantil. Primero, tomamos el valor reportado del ICT para cada hogar y, de acuerdo con la entidad federativa de pertenencia, se calcula su probabilidad acumulada según la distribución teórica ajustada sin restricción alguna, donde n_i es el número de hogares en la entidad i. Enseguida, se obtiene el valor estimado del ICT_ fase1 para cada hogar usando la función cuantil: .

De esta manera, obtenemos para cada hogar en toda la muestra un valor del ICT imputado que está determinado en función de los resultados del ajuste por entidad, ICT_fase1__h = ŷ_h ∀ h = 1,2,…,n.

Finalmente, el nuevo vector del ingreso por trabajo principal (ITP_ ajustado) se obtiene como sigue:

• Para cada hogar de la muestra tenemos dos valores: ICT original y el ICT_ fase1. Esto nos permite obtener un factor de corrección para cada hogar h,
  
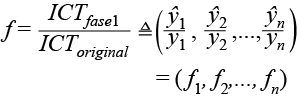
• Calculamos un nuevo valor del ITP para cada hogar de la siguiente manera:
  

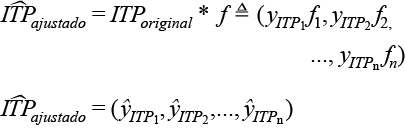
El factor de ajuste f solo es aplicado al ITP debido a que buscamos ajustes diferenciados (no en la misma proporción) para el ITP y para el ITP^C, ya que las mejoras operativas pudieron afectarlos de manera distinta (ver cuadro 2.4).

4.1 Resultados del ajuste al ITP de los hogares⁶

En este apartado presentamos los resultados del ajuste realizado al ingreso por trabajo principal (definido en el cuadro 2.5) de los hogares. El ITP promedio por hogar fue de 25 909 en el 2014, mientras que en la ENIGH 2016 fue de 28 373, ello representaría un incremento de 9.5% en términos reales. Con el ajuste descrito en el apartado anterior al ITP 2016, el promedio baja a 26 467, lo que equivale a un aumento de 2.1% con respecto al 2014.

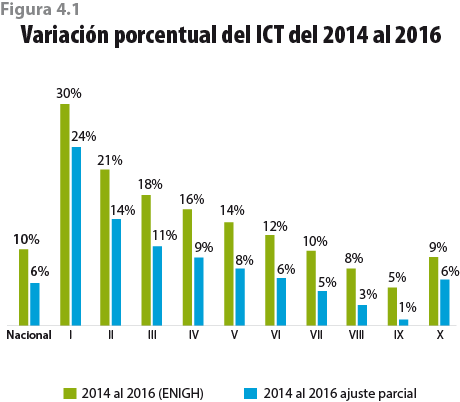
Si solo ajustamos el ITP y mantenemos el ITP^C originalmente reportado, el promedio por hogar del ICT sería de 44 615 pesos, equivalente a un aumento de 5.8% con respecto al MCS-ENIGH 2014. La figura 4.1 muestra las variaciones del ICT por decil que se tendrían al ajustar solo el ITP, es decir, bajo un ajuste parcial.

5. Ajuste al complemento del ITP

Un efecto colateral del ajuste realizado al ingreso por trabajo principal es que la proporción que históricamente guardaba (hasta antes del 2014) dentro del ICT se rompe con el ajuste de la sección anterior (ver figura 5.1). Este efecto es consecuencia de que solo se modifica una parte del ICT.
Si suponemos que en ausencia de las mejoras implementadas en la ENIGH 2016 la proporción entre el ITP y el ICT hubiese sido similar a la histórica (61.5% en promedio del 2010 al 2014),⁷ entonces podemos calcular el total del ingreso que no es ITP, tal que la proporción entre el ITP e ICT sea consistente con lo histórico. Es decir, llamemos ITP^c a la diferencia entre el ICT y el ITP. Después del ajuste al vector del ITP (ITP^ajustado) observamos que, a nivel nacional, los totales de cada ingreso cumplen con la siguiente relación:

Sin embargo, esa proporción debería ser cercana a 61.5% para hacerla consistente con lo que se venía observando hasta el 2014. De ser así, y dado que el valor del T_ITP^ajustado es conocido, lo único que tendríamos que hacer para conocer el monto del T_ITP^c ajustado es el siguiente despeje:

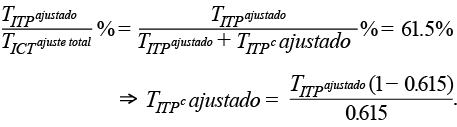
Si además dividimos lo anterior entre el número total de hogares, tendríamos el promedio por hogar que garantiza obtener 61.5%:

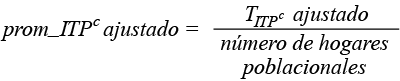(10)

Para distribuir el ajuste del ITP^C a los hogares, utilizamos de nuevo el marco metodológico desarrollado en la sección 3 y realizamos un procedimiento simétrico al de la sección anterior, aunque en este caso se hace un solo ajuste a nivel nacional; es decir, ajustamos una función de distribución GB2 al vector ITP^C para obtener un conjunto de parámetros ; después imponemos como restricción que el nuevo promedio de todos los microdatos del ITPC sea igual al prom_ITP^c ajustado, de esta forma obtenemos el segundo conjunto de parámetros .

Formalmente, el modelo con restricciones a resolver es el siguiente: sea H = {h: 1,2…, n} conjunto de hogares en la muestra, si suponemos que ITP^c ~ GB2(z|θ), entonces, el modelo con restricciones quedaría de la siguiente forma:

(11)

sujeto a:

a) Dos restricciones de igualdad.

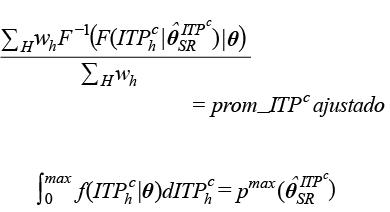
b) Restricciones de desigualdad: µ, υ, τ > 0 ; – ∞ < σ < ∞; – υ < 1 / σ < τ.

Donde max es el máximo valor del ITP^C y p^max () es la probabilidad acumulada (bajo la función teórica sin restricciones de ITP^C) correspondiente al valor max. F y f son las funciones acumulada y de densidad de la GB2, respectivamente. De este proceso se obtienen los parámetros restringidos .

La generación de los nuevos microdatos del ITP^C se realizó de la siguiente manera (ver figura 3.1): se toma el valor reportado del ITP^C para cada hogar y se calcula su probabilidad acumulada según la distribución teórica ajustada sin restricción alguna, , donde n es el número de hogares en la muestra. El nuevo valor estimado del ITP^C para cada hogar será entonces .

Así, el nuevo vector del ICT, , tendría un ajuste secuencial en dos etapas: 1) una donde se ajusta solo el vector de ITP y 2) otra donde solo se ajusta el vector de ITP^C. Los datos por hogar del nuevo vector del ICT, , están formados por cada uno de los dos procesos:

(12)

Por otra parte, y dado que el objetivo del ajuste es poder medir pobreza, es necesario trasladar el ajuste del ICT a todas las fuentes de ingreso monetario y no monetario que lo componen. Para transferir el efecto del ajuste, se calculan dos factores por hogar: y . Cada fuente de ingreso que forma el ITP se multiplica por α_h, mientras que las fuentes de ingreso que forman el ITP^C se multiplican por ß_h . Así se generan nuevas versiones de las tablas usadas por la metodología del CONEVAL para el cálculo de la pobreza.

6. Resultados

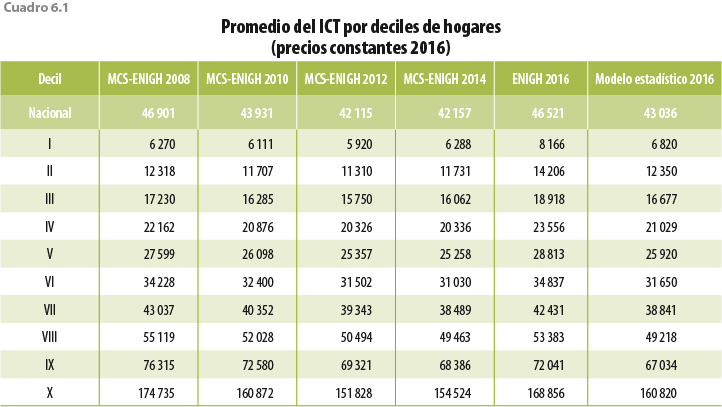
En los cuadros 6.1 y 6.2 se observa cómo con la ENIGH 2016 se obtienen ingresos considerablemente mayores a los históricamente reportados en los distintos deciles; de igual forma, podemos ver la magnitud del ajuste con el modelo estadístico 2016 y cómo éste recupera la continuidad histórica del ingreso. Si bien el primer decil es el que mayor crecimiento presentó en términos porcentuales, el aumento es similar al registrado entre el 2012 y 2014 (6.2%), periodo donde también fue el de mayor crecimiento
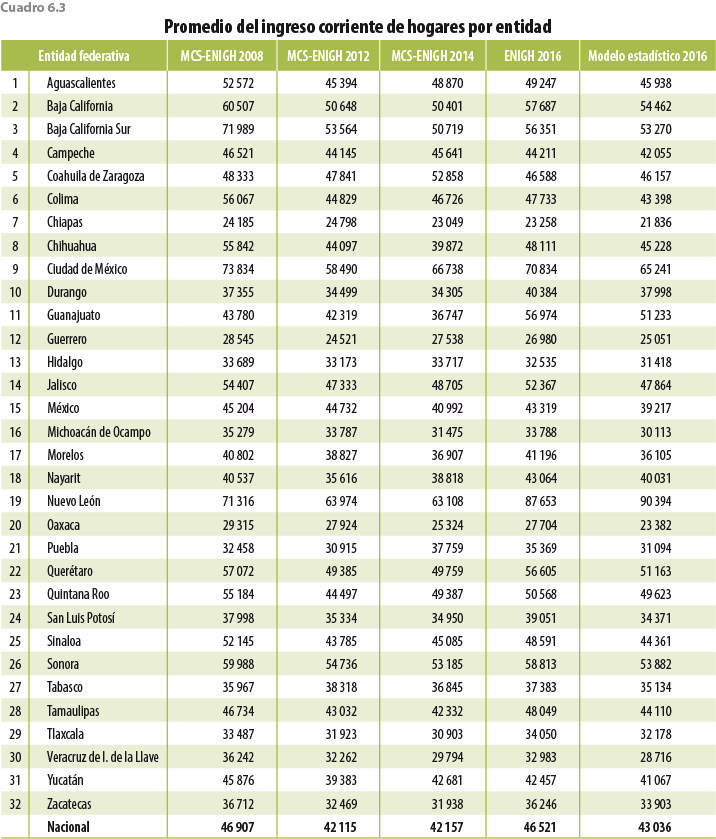
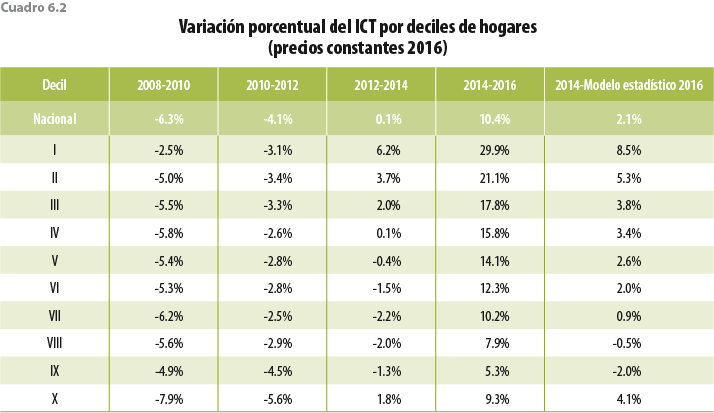Con respecto al comportamiento entre entidades, la ENIGH 2016 logra captar dos hogares cuyos ingresos son muy elevados, uno de ellos fue en Nuevo León y otro en Guanajuato. Esto es consecuencia del tamaño de muestra usado (por primera vez la ENIGH 2016 tiene representatividad a nivel entidad federativa y para los ámbitos rural y urbano), lo cual aumenta la probabilidad de captar hogares ricos o con ingresos muy elevados. Tanto en el cuadro 6.3 como en la figura 6.1 se observa la corrección del modelo estadístico para las distintas entidades federativas.
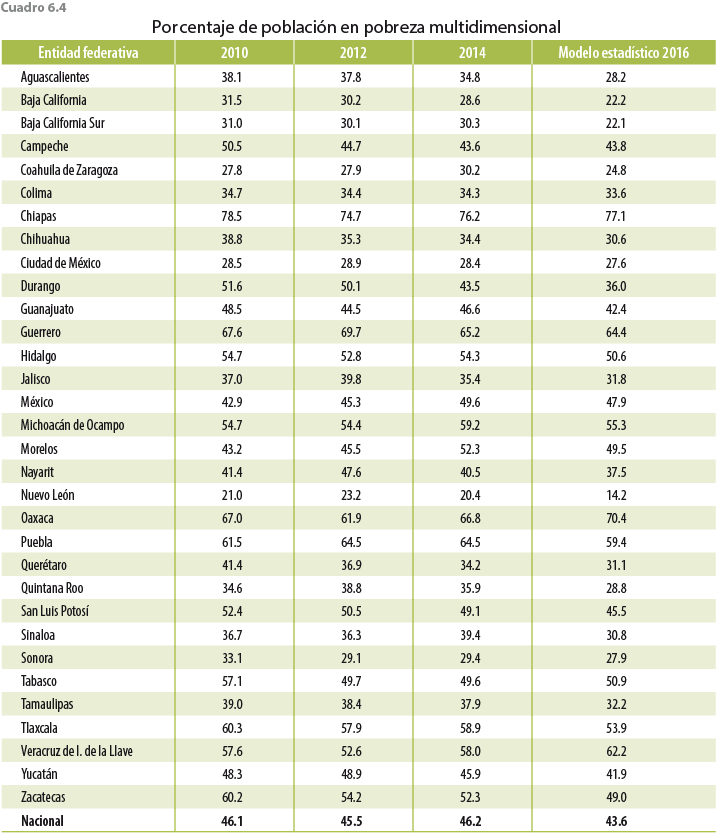
Con respecto a los cálculos de pobreza (ver cuadro 6.4), se consideró el ajuste a la carencia de seguridad social (adicional a los ajustes al ICT desarrollados en secciones anteriores) realizado por el CONEVAL: previo al levantamiento de la ENIGH 2016, el CONEVAL solicitó el cambio de fraseo para algunas preguntas relacionadas con el acceso a los servicios médicos y con otras dos prestaciones laborales que son consideradas para la identificación de la condición de carencia por seguridad social de la población trabajadora subordinada. Dicho cambio tuvo un efecto sobre la consistencia histórica de las respuestas que dan los informantes. La base de datos original de la ENIGH 2016 reporta tal cual los resultados del levantamiento en campo que resultan del nuevo fraseo. Sin embargo, buscando recuperar la continuidad de las series, se incorporan los resultados de un ejercicio estadístico que el CONEVAL diseñó para tal propósito. El ajuste se focaliza en la población trabajadora subordinada con acceso a servicios médicos como prestación laboral para recuperar la consistencia de la serie histórica de la carencia por acceso a la seguridad social.⁸
6.1 Estimación de los errores del modelo

La metodología desarrollada en este documento no es parte de las metodologías tradicionales de imputación/edición de microdatos, por lo que hasta la fecha no se cuenta con procedimientos estadísticos para la cuantificación de los errores en las estimaciones que arroja. Sin embargo, y aprovechando procesos como el de bootstrap, podemos generar mediciones que permitan tener un acercamiento a errores del modelo. Para ello, los cuadros 6.5 y 6.6 muestran el resultado de 500 repeticiones del algoritmo de ajuste del ingreso, con remuestras distintas obtenidas a través de bootstrap.
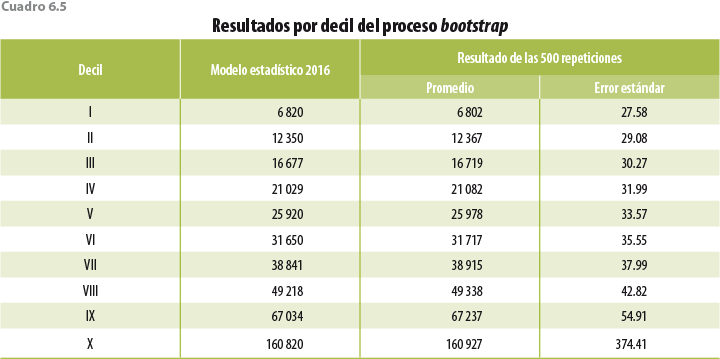
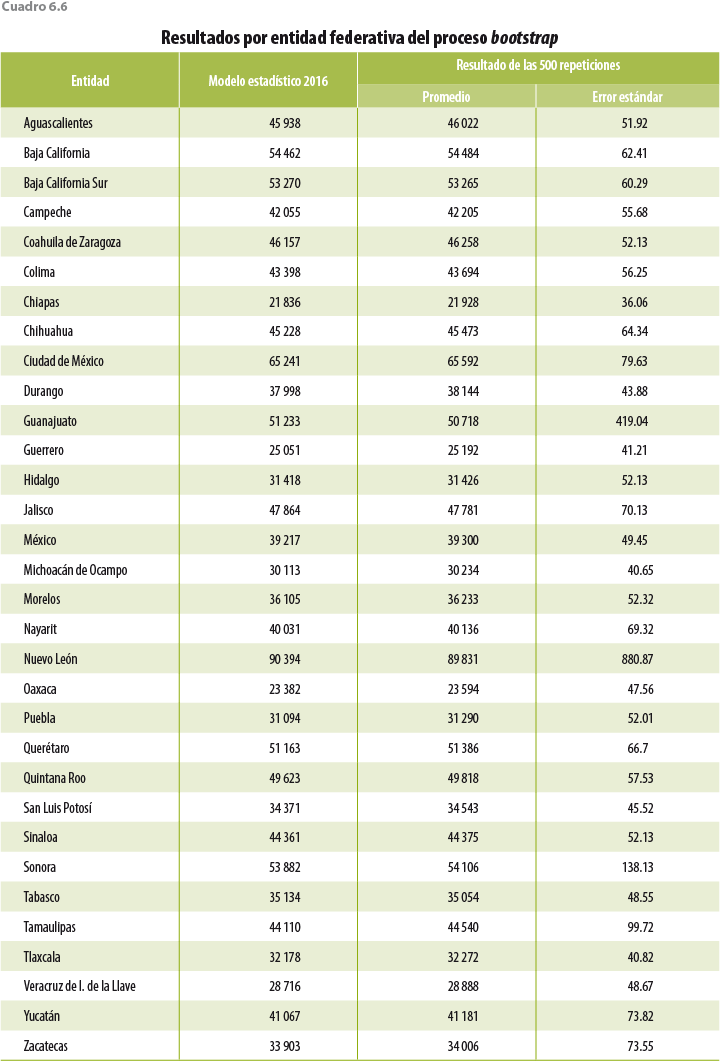Como se observa en ambos cuadros, el promedio de las 500 repeticiones es muy cercano a los datos reportados en los cuadros 6.1 y 6.3. Las entidades donde se observan las mayores distancias entre ambas estimaciones son Guanajuato, Nuevo León y Tamaulipas; de ellas, y como ya se ha mencionado, en las dos primeras se captaron hogares con ingresos muy elevados, lo que puede estar influyendo en las estimaciones.

7. Conclusiones

En un proceso continuo de mejora, el INEGI identificó áreas de oportunidad alrededor de la capacitación, supervisión y control operativo del MCS-ENIGH. A partir de ello, se llevaron a cabo acciones de fortalecimiento operativo en el levantamiento de la ENIGH 2016, en un esfuerzo por alcanzar un mayor apego al diseño de la encuesta.

La mayoría de los componentes del ICT tuvo un crecimiento considerable en la ENIGH 2016 con respecto a la información del MCS-ENIGH 2014. Uno de ellos es el ingreso del trabajo, el cual creció en este periodo 7.1% (para 2010-2012 y 2012-2014, las tasas de crecimiento fueron de 3.2 y 1.4%, respectivamente). Este rubro del ingreso ha representado más de 60% del ICT históricamente.

Los ingresos no laborales también crecieron de manera significativa; en términos del promedio por hogar, su crecimiento fue de 27% entre el 2014 y 2016, mientras que para el periodo 2012 al 2014 fue de solo 2.8 por ciento.

Debido al carácter único de la información que recopila la ENIGH, no existen otras encuestas con las cuales podamos comparar el comportamiento de sus distintas fuentes de ingreso. Sin embargo, la ENOE nos permite hacerlo para la fuente principal del ingreso de los hogares: los ingresos por trabajo principal. Una característica fundamental de la ENOE es que la recolección de información ha sido similar en los distintos levantamientos y que, por lo tanto, no sufrió cambios importantes en la captación de ingresos.

La metodología que aquí se propone edita los microdatos reportados a través de funciones de distribución. Primero, se ajusta una función de distribución conocida (GB2, en nuestro caso) a los datos muestrales y, con ello, se obtienen estimaciones de los parámetros que determinan la forma funcional de la función de distribución. Después, se realiza un proceso similar, pero imponiendo un conjunto de restricciones que debe cumplir el ajuste; estas condiciones involucran la obtención de valores puntuales (valores objetivo) de estadísticos muestrales, lo cual implica la modificación de los datos reportados en la muestra.

El proceso de ajuste se realizó por separado para el ITP y para los ingresos distintos a estos últimos (ITP^c ). Para obtener los valores objetivo de las restricciones impuestas, nos basamos en el crecimiento de la mediana de ingresos reportada en la ENOE; con ello modificamos el ITP. Los valores objetivo para las restricciones que entran en el ajuste al ^ITPc se obtuvieron de una relación empírica que se ha venido observando desde el 2010 entre el ITP^c y el ICT, y la cual asumimos que se debe mantener.

En términos de resultados, y considerando ambos ajustes (tanto al ITP como al ITP^c ), se logra que la variación entre el 2014 y 2016 del ICT promedio por hogar pase de 10.4 a 2.1 por ciento. El crecimiento para el primer decil es de 8.5% (en comparación con 29.9% al utilizar los datos de la ENIGH 2016). Cuando estos resultados se desagregan por entidad federativa, también se observan ajustes a la baja en las tasas de crecimiento para la mayoría de las entidades.

Referente a la medición de pobreza, una implicación de la disminución de los ingresos es el aumento en pobreza con respecto a los datos de la ENIGH 2016. Con el ajuste propuesto, la población en situación de pobreza multidimensional es de 43.6% (para el 2014 fue de 46.2%). Cabe mencionar que esta cifra de pobreza incorpora un ajuste adicional a la carencia por seguridad social realizada por el CONEVAL.

_____

Fuentes

Bandourian, Ripsy; James McDonald and Robert Turley. “A Comparasion of Parametric Models of Income Distribution Across Countries and Over Time Across Countries and Over Time”, en: Luxembourg Income Study Working Paper No. 305. 2002.

Bustos, Alfredo. “Estimation of the distribution of income from survey data, adjusting for compatibility with other sources”, en: Statistical Journal of the IAOS. Journal of the International Association for Official Statistics. Vol. 31, no. 4, noviembre del 2015, pp. 565-577.

García, Carmelo; Mercedes Prieto e Hipólito Simón. La modelización paramétrica de las distribuciones salariales. Un estudio aplicado al caso español. Universidad de Alicante, Departamento de Análisis Económico Aplicado, junio del 2012, 31 pp.

Graf, Monique; Desislava Nedyalkova; Ralf Münnich; Jan Seger and Stefan Zins. Parametric estimation of income distributions and indicators of poverty and social exclusion. Advanced Methodology for European Laeken Indicators. Sevent Framework Programme, 2011, 74 pp.

McDonald, James B. “Some generalized functions for the size distribution of income”, en: Modeling Income Distributions and Lorenz Curves. Capítulo 3. Mayo de 1984, pp. 37-55.

McDonald, James B. and Michael Ransom. “The Generalized Beta Distribution as a Model for the Distribution of Income: Estimation of Related Measures of Inequality”, en: Modeling Income Distributions and Lorenz Curves. Cap. 8. Economic Studies in Inequality Social Exclusion and Well-Being. Springer, 2008, pp. 147-164.

McDonald, James B. and Yexiao J. X. “A generalization of the beta distribution with applications”, en: Journal of Econometrics. Vol. 66, Issues 1-2, marzoabril de 1995, pp. 133-152.

Rigby, R. A. and D. M. Stasinopoulos. “Generalized additive models for location, scale and shape”, en: Appl. Statist. 54, Part 3. 2005, pp. 507-554.

Singh, S. K. and G. S. Maddala. “A function for size distribution or incomes”, en: Modeling Income Distributions and Lorenz Curves. Vol. 44. Septiembre de 1976, pp. 963-970.

Skinner, C.; D. Holt and T. Smith (editors). Analysis of Complex Surveys. New York, USA, John Wiley and Sons, 1989.

Stasinopoulos, Mikis; Bob Rigby and Calliope Akantziliotou. Instructions on how to use the gamlss package in R. Second edition. Enero del 2008, 206 pp.

_____

Anexo 1

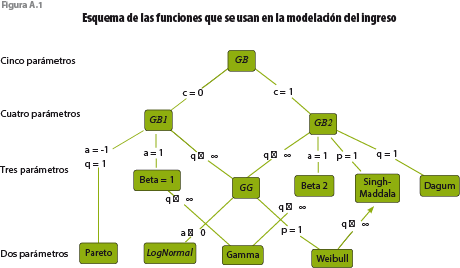
En estudios previos, y para distintos países, se han probado familias de distribuciones para ajustar variables, como ingreso y salario, con resultados satisfactorios. Algunas de las funciones más utilizadas se muestran en la figura A.1 obtenida de Bandourian et al. (2002).

La siguiente parametrización de las formas funcionales elegidas para el estudio puede ser encontrada en el documento Instructions on how to use the gamlss package in R.

Beta Generalizada tipo 2: GB2 ( µ, σ, υ, τ )

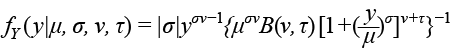
Para y > 0, donde µ, υ, τ > 0, – ∞ < σ < ∞ y – υ< ¹/_σ < τ .

Dagum

Dagum (y|μ, σ, ν) = GB2 (y|μ, σ, ν, τ =1)

Gamma Generalizada: GG ( µ, σ, υ)

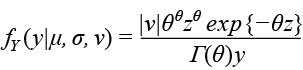
Para y > 0, donde µ > 0, σ > 0 y – ∞ < υ < ∞. Y donde y θ = 1/(σ² υ² ).

LogNormal distribución: LogNor (µ, σ )

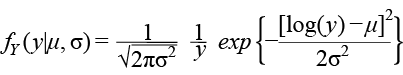
Para y > 0, donde µ > 0 y σ > 0.

Aquí E (Y) = ω^1/2 e^µ y Var (Y) = ω(ω – 1)e^2µ , donde ω = exp(σ² ).

Anexo 2

Para determinar la función paramétrica a utilizar, realizamos algunas pruebas de bondad de ajuste y elementos de visualización que nos permitieran elegir la función que mejor se ajusta a los datos empíricos. El resultado fue la selección de la función GB2 para nuestro modelo.

Estadísticos para pruebas de bondad de ajuste  Definimos: wi = número de hogares que representa el ingreso yi . SSE suma del cuadrado de errores Estadístico x2 Log-verosimilitud Aikaike BIC K = número de parámetros.

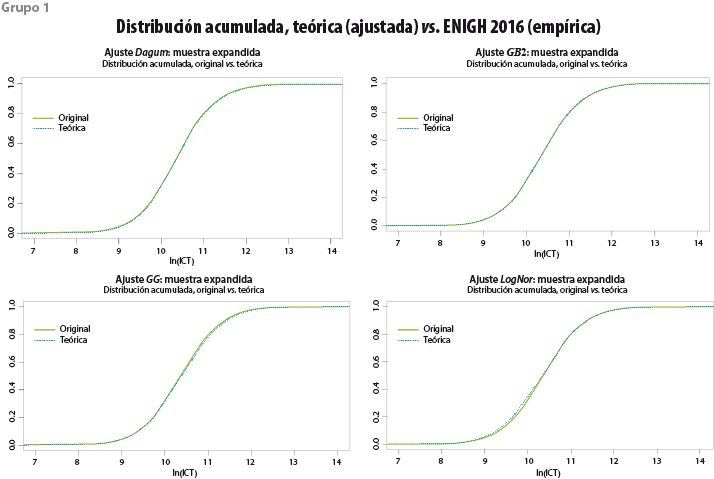
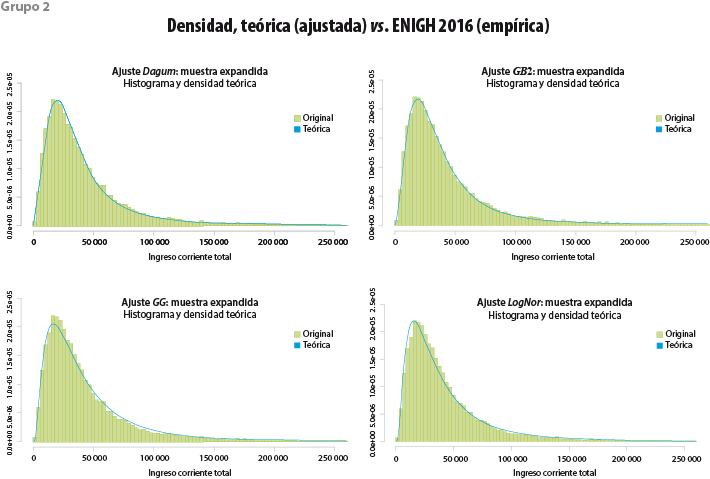
Visualización Función de densidad En primera instancia se puede comprobar si la función elegida se adecua al histograma de los datos observados en la encuesta (ver grupo 2 de gráficas). Función de distribución acumulada En el grupo 1 se muestran las probabilidades acumuladas que asigna la función teórica a los ingresos observados . pp-plot En el grupo de gráficas 3 refleja la discrepancia para cada observación de la muestra con respecto a los valores que la función del modelo teórico pronostica; cuanto más se aproximan a la diagonal del cuadrante la calidad del ajuste es mejor.

_____

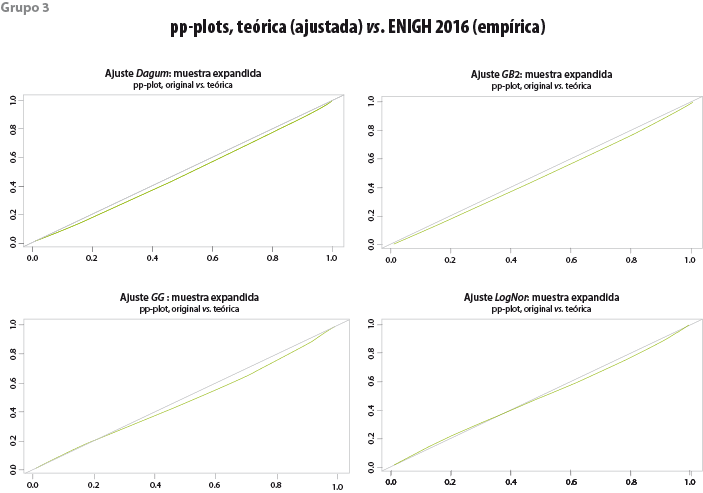
¹ Salvo en el primer trimestre del año, el ingreso laboral de la ENOE hace referencia al correspondiente originado por el trabajo principal.

² A menos que se especifique lo contrario, las cifras reportadas para años anteriores al 2016 son referidas a los datos conjuntos del MCS-ENIGH.

³ La mayoría de usuarios que elige este método de estimación prefiere usar la siguiente regla de equivalencia: maximizar una función es matemáticamente equivalente a minimizar la expresión negativa de la función objetivo, es decir, Max [l(θ)] ≡ Min [-l(θ)] ; la preferencia radica en que, computacionalmente, los algoritmos están adaptados para la minimización de funciones.

⁴ En caso contrario, el modelo expresado en (6) se convierte en la solución de un sistema de ecuaciones sin la dependencia de los valores observados de la variable aleatoria Y.

⁵ Éstas fueron elegidas debido a que han sido muy usadas en la modelación del ingreso en distintos países con resultados satisfactorios.

⁶ El software estadístico que se utilizó para implementar la metodología descrita fue R versión 3.4.0 (de uso libre) a través de su IDE RStudio versión 1.0.143. Las librerías usadas son:
• foreign_0.8-67
• gamlss_5.0-2
• alabama_2015.3-1
• survey_3.32
• plyr_1.8.4
• dplyr_0.7.0
• GB2_2.1
Los resultados pueden variar dependiendo de las características del sistema de la computadora utilizada; el procesamiento del algoritmo fue realizado en un equipo con las siguientes características: Lanix con procesador AMD FX-8370 de ocho núcleos y 4.00 GHz, sistema operativo de 64-bits.

⁷ La razón de tomar la proporción histórica (y no la observada en la ENIGH 2016) es que el modelo tiene como objetivo hacer los datos de la ENIGH 2016 comparables con la trayectoria que se venía observando, incluida la relación entre el ITP y su complemento.

⁸ Para mayores detalles véase: bit.ly/4d0kTE0