Actualización del Sistema de Indicadores Cíclicos de México

 

Updating the Mexican System of Cyclical Indicators

 

Víctor Manuel Guerrero Guzmán* y Francisco de Jesús Corona Villavicencio**
* Instituto Tecnológico Autónomo de México (ITAM), guerrero@itam.mx
** Instituto Nacional de Estadística y Geografía (INEGI), franciscoj.corona@inegi.org.mx

Nota: en primer lugar, se agradecen los comentarios y sugerencias de dos revisores anónimos. Este proyecto se llevó a cabo gracias al apoyo de los siguientes funcionarios del INEGI: E. Ordaz, G. Leyva, y Y. Yabuta. De igual forma, J. Martínez, y L. Montoya ayudaron a realizar el estudio al facilitar algunos programas de cómputo, documentos y archivos de datos que les fueron solicitados, así como por sus comentarios y sugerencias. También se agradece la participación de J. López en la parte final del proyecto para revisar los resultados numéricos y las conclusiones del estudio. V. Guerrero participó en este proyecto gracias a un periodo sabático otorgado por el ITAM y al apoyo de la Asociación Mexicana de Cultura, AC.

 

Vol.9, Núm.3 – Epub                                         Actualización del Sistema… Epub

En este trabajo se analiza la adecuación del método de estimación de los indicadores coincidente y adelantado, en el marco de análisis actual del Sistema de Indicadores Compuestos Coincidente y Adelantado del INEGI, y se asigna incertidumbre a los ciclos estimados para que sea más clara y objetiva la identificación de sus fases. La técnica se complementa con el uso de un modelo de factores dinámicos que apoya la propuesta que se hace. Como resultado de la investigación, se recomienda calcular los indicadores compuestos con un filtro diferente al que se usa en el INEGI, incluir en el indicador adelantado una variable adicional para mejorar su capacidad de adelanto, utilizar bandas de tolerancia para asignar incertidumbre a la estimación de los ciclos y regularizar el periodo de actualización del Sistema de Indicadores Compuestos para mantenerlo vigente al paso del tiempo.                                  Palabras clave: diferencia significativa; estado de la economía; estimación de tendencia; filtro de Hodrick-Prescott; modelo dinámico de factores.

We analyze the adequacy of the estimation method of the coincident and leading indicators within the context of the current INEGI’s System of Composite Coincident and Leading Indicators. We propose a method to assign uncertainty to the cycle estimates in order to identify its phases more clearly and objectively. This work is complemented with the application of a Dynamic Factor Model whose results back up our proposal. As a result of this study, we recommend to calculate the indicators with the aid of a different filter from the current one at use in INEGI; we also recommend to include a new component variable in the leading indicator to improve its leading ability; to employ the tolerance bands here derived to appreciate the uncertainty of the cycle estimates; and to regularize the revising span of the System of Composite Indicators to keep it updated along time.                                    Key words: significant difference; state of the economy; trend estimation; Hodrick-Prescott filter; dynamic factor model.

Recibido: 24 de noviembre de 2017.
Aceptado: 4 de abril de 2018.

 

Introducción

El presente estudio está orientado hacia el análisis de ciclos de la economía mexicana desde la perspectiva de la revisión y justificación estadística de los métodos que se usan actualmente en el Instituto Nacional de Estadística y Geografía (INEGI) para realizar el cálculo de los indicadores compuestos (coincidente y adelantado).

Para realizar un análisis econométrico basado en este tipo de indicadores, se parte del supuesto de que es factible descomponer una serie de tiempo en diversos elementos que subyacen en la misma y que le transfieren sus características específicas. Por ello, típicamente, se considera que las series de tiempo económicas están formadas por componentes que no son observables directamente (como la tendencia de largo plazo, el ciclo, la estacionalidad y otros efectos) que incluyen un elemento irregular de comportamiento aleatorio. La manera en la que los componentes se unen para formar la serie observada es por lo común mediante una suma ponderada —y lo mismo se hace en este trabajo— aunque en ocasiones alguna serie requiere ser transformada con la aplicación del logaritmo para que sus componentes puedan sumarse.

Algunas consideraciones sobre indicadores cíclicos en México

La construcción de los indicadores cíclicos inicia con la selección de variables potencialmente útiles para constituir el indicador compuesto. Para ello, se debe cumplir con los requisitos señalados por la Organización para la Cooperación y Desarrollo Económicos (OCDE), según se indica en OECD (2012): (i) que la variable en cuestión tenga relevancia económica, en el sentido de que su relación con la variable indicadora de referencia admita interpretación económica clara y (ii) que su cobertura sectorial sea lo más amplia posible, para que represente alguna actividad económica en general. Asimismo, desde el punto de vista práctico, se requiere de la variable: a) que su periodicidad de observación sea mensual, b) que sus datos no estén sujetos a revisiones frecuentes, c) que su información se publique con oportunidad y d) que el registro de datos históricos de la serie tenga la longitud suficiente para poder apreciar en ella la evolución de los ciclos económicos.

En septiembre del 2014, el INEGI llevó a cabo un taller sobre el Sistema de Indicadores Cíclicos (SIC) de México para consultar a analistas especializados y conocer sus opiniones acerca de las series que deberían formar parte del mismo; de ahí sugirieron 67 variables que pudieran ser componentes de los indicadores compuestos. No todas las que se sugieran deben incluirse de manera automática, sino que tienen que ser sometidas a un proceso riguroso de análisis para determinar su utilidad como componente de alguno de los indicadores compuestos; realizar esta labor requiere de un gran esfuerzo y dedicación por personal especializado. Además, debe tenerse presente que el SIC cuenta con dos indicadores compuestos: el Coincidente (IC) y el Adelantado (IA). El primero permite observar el estado general de la economía, mientras que el segundo pretende anticipar la trayectoria que seguirá el IC en el corto plazo, en especial en lo que se refiere a los puntos de giro, es decir, a las crestas y los valles que forman los ciclos económicos.

El documento Metodología para la construcción del Sistema de Indicadores Cíclicos (INEGI, 2015) menciona que el indicador global de la actividad económica (IGAE) fue seleccionado como serie de referencia para definir los componentes del IC, que mide en forma aproximada el comportamiento cíclico de la economía agregada y sirve de referencia para seleccionar variables cuyas crestas y valles coincidan con los del IGAE. Para esto, fue necesario trabajar con todas y cada una de las series propuestas, previamente ajustadas por estacionalidad y corregidas por valores atípicos. También se tuvo cuidado de mantener la interpretación del indicador respectivo, ya que algunas series muestran un comportamiento contrario al de la actividad económica en general, tal es el caso de la tasa de desocupación urbana (TDU), del tipo de cambio real (TCR) bilateral México-Estados Unidos de América (EE.UU.) y de la tasa de interés interbancaria de equilibrio (TIIE), por lo que estas series que son contracíclicas se pueden convertir en procíclicas al usar el inverso (el signo contrario) del indicador al momento de incorporarlas al indicador compuesto que les corresponde.

El IGAE se usa de referencia únicamente en la etapa inicial de construcción de los índices y, posteriormente, es uno más de los componentes del IC; esto se debe a que mide la producción económica, que es solo uno de los aspectos que interesa estudiar del estado de la economía. Otras situaciones se refieren a las ventas, al empleo y al ingreso real, las cuales también se ven afectadas cuando se presenta una recesión, que es el fenómeno fundamental que se quiere monitorear con el IC y anticipar con el IA. En el mencionado documento metodológico del INEGI (2015) se mencionan los cambios resultantes de la actualización del 2014 respecto al SIC establecido en el 2010 (ver Guerrero, 2013): el IC usa el IGAE en lugar del indicador de la actividad económica mensual que antes se utilizaba; en el IA se sustituyó el tipo de cambio real (multilateral) por el TCR bilateral, se incorporó el indicador de confianza empresarial: momento adecuado para invertir (CSAAM) del sector manufacturero y se excluyó exportaciones no-petroleras.

En consecuencia, el IC está compuesto actualmente por el IGAE, el indicador de la actividad industrial (IAI), el índice de ingresos por suministro de bienes y servicios al por menor (IISBS), asegurados trabajadores permanentes en el IMSS (ATPIMSS), la TDU e importaciones totales (IT). Por otra parte, al IA lo componen la tendencia del empleo en las manufacturas (TEM), el CSAAM, el índice de precios y cotizaciones de la Bolsa Mexicana de Valores en términos reales (PONMB), el TCR bilateral, la TIIE y, finalmente, el índice Standard & Poor’s 500 (ISP500).

Aportaciones de este trabajo

Aquí se retoman los resultados obtenidos en el 2014 y se efectúa una nueva actualización enfocada en los métodos estadístico-econométricos utilizados por el INEGI para calcular los indicadores compuestos. Conviene recordar que existen dos enfoques básicos para el análisis de los ciclos económicos: el clásico de negocios y el de crecimiento, los cuales usan distintas definiciones de lo que es un ciclo. Por un lado, el del primero se refiere a los movimientos cíclicos, como los que ocurren cuando la actividad económica disminuye y después aumenta en relación con el nivel alcanzado; este enfoque lo utiliza el Conference Board de EE.UU., organismo que se encarga de calcular los Business Cycle Indicators de ese país de manera oficial. Por el otro lado, el ciclo de crecimiento mide la fluctuación cíclica como desviación respecto a la tendencia de largo plazo, lo cual implica estimarla como un paso fundamental del método, y es la visión que sigue la OCDE. Los dos enfoques están relacionados entre sí, como lo demuestran Anas y Ferrara (2004) y, por ello, los indicadores para el ciclo clásico se pueden obtener a partir del de crecimiento cuando se restaura la tendencia.

Uno de los principales resultados de los estudios previos es que el enfoque de ciclo de crecimiento es preferible al clásico, como lo señala Guerrero (2013). Por consiguiente, se mantiene la idea de aplicar el método de la OCDE, aunque se pone a prueba la estimación de tendencias con aplicación doble del filtro de Hodrick-Prescott (HP) para fijar el paso de banda de las frecuencias cíclicas. Por ello, se experimenta con diversas opciones para no usar, necesariamente, el paso de banda de frecuencia cíclica con longitud de uno a 10 años que utiliza la OCDE, la cual puede ser válida en diversos países de la OCDE, incluido México, aunque la creencia popular en nuestra nación es que la frecuencia de los ciclos es mayor y que su duración es menor a los 10 años; por ello, conviene dejar a los datos mismos que señalen el paso de banda más apropiado.

También se revisa la pertinencia de las series que integran los componentes cíclicos y se busca algún criterio estadístico para determinar en qué momento los indicadores IC e IA, al igual que sus componentes, se encuentran alejados de forma suficiente de la tendencia para afirmar que están significativamente arriba o debajo de la misma en términos estadísticos. Esto es en particular importante para el IA, pues contiene algunas variables financieras que son volátiles y tienden a brindar señales erráticas. Con la propuesta que resulta de este trabajo se busca evitar señales falsas y, en general, obtener indicadores con solidez estadística. Esto ayudará a los usuarios de la información a monitorear con más oportunidad los puntos de giro en el ciclo económico y tomar decisiones con mayor certeza.

En este artículo se presenta, en primera instancia, el método para estimar la tendencia de una serie de tiempo, donde se aprecia la posibilidad de asignar incertidumbre estadística a la estimación, lo cual hace factible construir bandas alrededor de la misma, y se muestra la manera de elegir el parámetro de suavizamiento en función del paso de banda para la frecuencia cíclica que se decida utilizar. Enseguida, se analiza la estabilidad del ciclo estimado en lo que toca a sus revisiones y se estudia la oportunidad del indicador para detectar puntos de giro, con lo cual se puede elegir las variables que deben incluirse o excluirse de los indicadores; como resultado de este análisis se encuentra que sí es necesario cambiar el paso de banda de la frecuencia cíclica, lo que produce nuevos indicadores cíclicos. Posteriormente se expone el método de factores dinámicos para la construcción de indicadores compuestos, que es válido si un solo factor resume bien la variabilidad de los datos observados, como ocurre en la presente aplicación empírica; el factor subyacente estimado complementa la información que brinda el indicador y, por ello, se propone combinarlos con el criterio estadístico de varianza mínima. Se muestran entonces los resultados numéricos de la aplicación de los métodos propuestos y se encuentra que el método en uso en el INEGI no requiere cambios de los componentes del IC, pero sí puede mejorarse al añadir un nuevo componente al IA. Además, la estimación del ciclo se acompaña ahora con una banda de tolerancia alrededor de la tendencia de largo plazo para distinguir los movimientos cíclicos de los de tendencia.

Estimación de la tendencia y de su varianza

El método que utiliza la OCDE para estimar la tendencia de una serie de tiempo es el filtro HP doble, que consiste en dos aplicaciones sucesivas del de Hodrick y Prescott (1997). En el presente trabajo se ve a dicho filtro desde la perspectiva estadística propuesta por Guerrero (2007), la cual considera a la tendencia como una serie de tiempo no-observada que puede estimarse, al igual que su varianza, con los datos de la serie originalmente observada. Por ello, se puede calcular una franja o banda de tolerancia alrededor de la tendencia estimada, de manera que los valores que se encuentren dentro de ella no se consideren distintos de la tendencia verdadera, es decir, que sean tolerables —o equivalentes— en términos estadísticos. En este sentido se hablará de tolerancia, sin asignar necesariamente un nivel de confianza o de probabilidad para la cobertura de valores dentro de ella. No es suficiente considerar el valor de la tendencia en cada momento de observación como una estimación puntual, sino que se podrá hacer mención a la estimación por intervalo. Esta idea se formaliza con el Teorema de Tchebysheff (ver Wackerly et al., 2002, Ch. 4), que asigna probabilidad a los intervalos individuales para la tendencia verdadera, como se verá más adelante.

Con la franja sugerida se definen con mayor claridad algunos términos usados en el documento metodológico del INEGI (2015) en referencia a las cuatro fases del ciclo económico y cómo se les puede identificar mediante el IC. Las fases se determinan en términos del componente cíclico del indicador, que son: 1) expansión, si crece y se ubica por arriba de la tendencia de largo plazo (mostrada como una línea con valor 100); 2) desaceleración, si decrece y está arriba de la tendencia; 3) recesión, si decrece y está debajo de la tendencia; y 4) recuperación, si crece, pero se ubica debajo de la tendencia. La figura 1 ilustra el comportamiento cíclico de una variable hipotética, con sus cuatro fases, referidas al valor 100 de la tendencia.

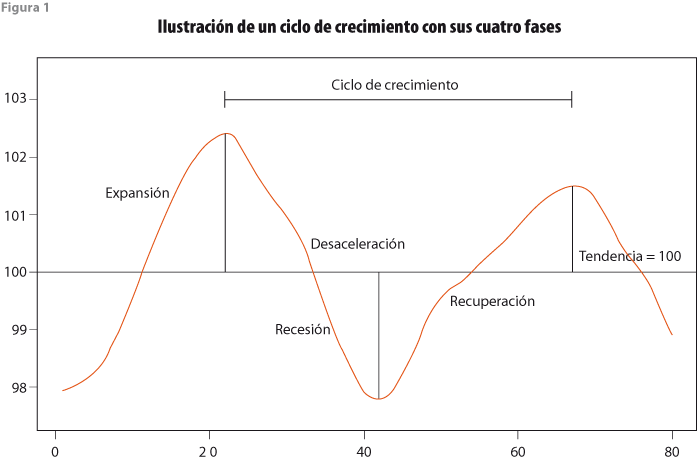
En lugar de usar un solo número para indicar el valor de referencia, se considerará una franja de valores alrededor del 100 como equivalentes en términos estadísticos. La banda es útil, también, para apoyar ideas como la de Bandholz y Funke (2003) en contra del argumento que se usa en EE.UU. para señalar que, cuando el producto interno bruto (PIB) decrece durante dos trimestres consecutivos, entonces la economía entra en recesión. De hecho, estos autores señalan que tiene más sentido definir una recesión como el periodo durante el cual el PIB cae de manera significativa por debajo de su tendencia potencial. Desde luego, es preferible considerar el IC y no solo el PIB para llegar a esta conclusión. Por lo mismo, se debe considerar la tendencia estimada del IC y su varianza para construir la banda, la cual se puede utilizar para comparar cada uno de los ciclos estimados de las series que componen a los indicadores compuestos, al igual que los ciclos del IC y del IA mismos.

Filtro HP y varianza de la tendencia

Para estimar la varianza de la tendencia, se parte del método que sustenta al filtro HP, que es mínimos cuadrados penalizados (MCP), de manera que se considera el problema de minimizar una función cuadrática M( λ ) que depende de la constante de penalización λ , conocida como parámetro de suavizamiento; es decir, se debe resolver el problema:

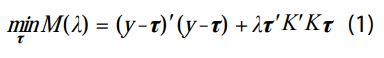
donde aparece el vector de datos observados y=(y₁,… ,y_N)ʼ correspondientes a una serie de tiempo {y_t}, así como el vector de tendencia τ=(τ₁,… ,τ_N)ʼ que se asocia con la serie de tiempo {τ}. La serie {y_t} contiene las observaciones ajustadas por estacionalidad y valores atípicos de uno de los indicadores en consideración. Además, el apóstrofo indica transposición y K es una matriz de dimensión (N-2) × N, cuya diagonal central es una lista de valores -2 y las diagonales inferior y superior alrededor de la central contienen 1’s.

La solución estándar se obtiene al derivar M( λ ) respecto a τ , igualar a 0 la derivada evaluada en y resolver la ecuación resultante, lo cual da como resultado:

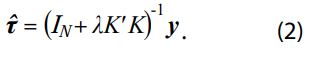
En la aplicación que hace la OCDE del filtro HP, éste es el único resultado que se utiliza. Sin embargo, se puede extraer información acerca de la incertidumbre en la estimación, ya que el mismo resultado se obtiene con un método de estimación más de carácter estadístico, que tiene en cuenta la aleatoriedad de la variable involucrada. En Guerrero (2008) se muestran otras maneras alternativas y equivalentes de obtener el resultado (2), las cuales se usan en relación con el filtro de Kalman o con el de Wiener-Kolmogorov.

Para incorporar la aleatoriedad, se usa el modelo de componentes no-observables que subyace en la aplicación del filtro HP, esto es, se introduce un vector de errores aleatorios η=(η₁,… ,η_N)ʼ y se postula el siguiente modelo de tendencia más ciclo:

La descripción estadística de la tendencia usa el vector aleatorio ε=(ε₃,… ,ε_N)ʼ:

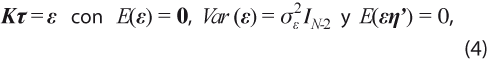donde σ²_η y σ²_ε son las varianzas de los componentes y de error en la tendencia, respectivamente, que conducen al parámetro de suavizamiento λ=σ²_η/σ²_ε.

Al aplicar el método de mínimos cuadrados generalizados (MCG) a las ecuaciones (3) y (4) se obtiene el estimador con error cuadrático medio (ECM) mínimo:

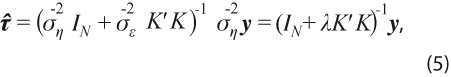que es el mismo del filtro HP, ver la expresión (2). Además, ahora se obtiene la matriz de ECM del estimador:

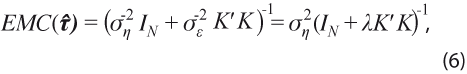
con la que se puede medir la incertidumbre en la estimación. Para estimar el valor de σ²_η , se usa el estimador insesgado propuesto en Guerrero (2007):

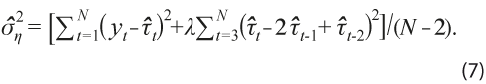Esta expresión es útil en relación con el análisis de ciclos, pues proporciona una medida escalar de la incertidumbre asociada con el uso del filtro HP y se usa en este trabajo para generar una banda de tolerancia de k ≥ 1 veces el error estándar de la estimación alrededor de la línea de tendencia.

Se dirá que un cierto valor τ_t puede tolerarse como representante de la tendencia en el tiempo t si se encuentra dentro del intervalo de , donde representa el error estándar estimado de la tendencia estimada, que surge como raíz cuadrada del elemento t-ésimo en la diagonal de . Dicha tolerancia se asocia con un valor mínimo de probabilidad de ocurrencia mediante el Teorema de Tchebysheff, el cual establece que para un valor k≥ 1, se cumple que al menos una proporción 1 − 1/k² caerá dentro de la banda de ± k errores estándar alrededor de la media. Esto se usa para afirmar que en cada momento de observación t se obtiene la probabilidad:

 

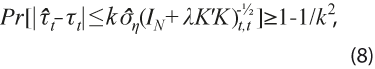
donde el subíndice t,t indica el elemento de la respectiva matriz, que corresponde a .

El valor producido por (8) es una probabilidad mínima ya que, por ejemplo, si fuera válido suponer normalidad para el estimador de la tendencia, el valor 1 − 1 / k² = ³/₄ con k = 2 aumentaría a 95.4% y, si la distribución fuese uniforme, dicho valor sería 100% (ver Wackerly et al., 2002). Por otro lado, debe recordarse que la serie {y_t } a la que se aplica el filtro HP está ajustada por estacionalidad y valores atípicos, de manera que sus bandas de tolerancia no son apropiadas para juzgar el comportamiento de la serie original. En McElroy (2006) se hace mención a este hecho porque al analizar ciclos primero se ajusta la serie por estacionalidad, así que se debe tener cuidado con las conclusiones que se obtengan. Por este motivo, en este trabajo se usan las bandas de tolerancia obtenidas con (7) como una referencia un tanto burda de la variabilidad de la serie, que serían apropiadas para hacer análisis de ciclos en niveles —con enfoque de ciclo clásico—; en cambio, para juzgar mejor el patrón del ciclo de crecimiento, es preferible usar el procedimiento que se muestra más adelante.

Elección del parámetro de suavizamiento

Como se puede apreciar en las expresiones (5) a (7), para aplicar el filtro HP al vector de datos y se requiere proporcionar el valor del parámetro λ. Para determinar este valor, se podría usar un argumento del dominio del tiempo, como en Guerrero (2007, 2008), donde se fija un porcentaje de suavidad deseado para la tendencia y se deduce el valor del parámetro, lo cual es válido cuando interesa estudiar la tendencia y no necesariamente el ciclo de las series en consideración; o bien, se puede emplear un argumento del dominio de frecuencias, como lo sugiere la OCDE (ver OECD, 2012) para analizar ciclos económicos, el cual se considera más apropiado para el presente estudio y, por tal motivo, la fórmula que se aplica de manera que el ciclo se complete en T meses es la siguiente:

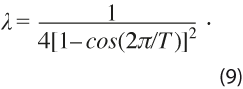
En la primera aplicación del filtro HP se elige el punto de corte para las frecuencias con T = 120 meses, por lo que la constante que resulta para eliminar la tendencia y mantener las fluctuaciones que se repiten a lo más cada 120 meses es λ = 133107.9. En la segunda se usa el filtro para eliminar del componente cíclico las fluctuaciones de alta frecuencia, que son básicamente irregulares y no pertenecen propiamente al ciclo. Esto se logra al cortar frecuencias de T = 12 meses con λ = 13.9. Al aplicar el filtro HP de acuerdo con este método de la OCDE se obtiene entonces un filtro de paso de banda que retiene en la serie filtrada las fluctuaciones cíclicas, cuyas frecuencias cubren el periodo de 12 a 120 meses.

Análisis de estabilidad y confiabilidad de los ciclos

Como no es necesariamente cierto que el paso de banda de 12 a 120 meses sea adecuado para las series que forman el SIC de México, se decidió probar distintas longitudes de ciclos para elegir el apropiado según sus resultados empíricos. También se busca que el método sea robusto ante la inclusión de nuevos datos —lo cual conduce a revisar la estimación del ciclo— y que proporcione señales oportunas y estables al paso del tiempo, como señalan Nilsson y Gyomai (2008). Esto podría conducir a elegir nuevas variables para que ingresen al SIC y a descartar otras que ya se encuentren dentro del Sistema.

Evaluación de los ciclos: revisiones

La evaluación del comportamiento cíclico de las variables se debe realizar al echar a andar un sistema de indicadores como el SIC o cuando se actualiza el Sistema para que mantenga su relevancia y credibilidad, como sucedió en el 2014, al igual que en el presente caso en que ya está funcionando el SIC para México. Es la tarea más laboriosa y lenta del proceso, pues una vez seleccionados los componentes y construidos los indicadores compuestos, el mantenimiento del Sistema es relativamente simple. Los estadísticos que se utilizan en esta fase se refieren a la estimación del ciclo con diferentes cosechas de datos, es decir, para estimar el valor del ciclo en el tiempo t, se usan datos de la cosecha al tiempo t + i, con lo que se obtiene la estimación del ciclo así se realiza la revisión de la estimación realizada con datos disponibles en el periodo t + i – 1, la cual está dada por la diferencia:

Cada valor de i = 1, …, n corresponde a una nueva cosecha de datos y de revisiones. También se considera el efecto acumulado de las revisiones:

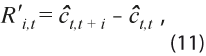
donde indica la primera estimación que se realizó del ciclo. El análisis se basa en las siguientes medidas o estadísticos, agrupados en los bloques (A), (B) y (C), como lo sugirieron Nilsson y Gyomai (2008) (ver también Di Fonzo, 2005):

(A) Tamaño:

• Revisión absoluta media: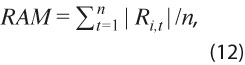mide el tamaño de las revisiones sin importar signo e incluye sesgo potencial, por no estar centrada en la media.
• Desviación estándar de las revisiones: 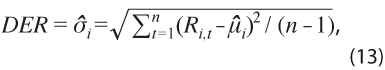mide la dispersión global de las revisiones y corrige el sesgo potencial que pudiera existir, además de dar énfasis a los valores extremos.
• Revisión absoluta acumulada: 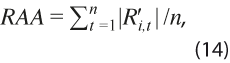mide la magnitud acumulada de las revisiones desde la primera estimación del ciclo y no tiene corrección por sesgo.

(B) Sesgo y autocorrelación:

• Revisión media: 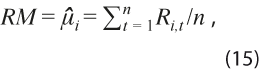refleja el sesgo en la estimación del ciclo, pero compensa revisiones de signos contrarios.
• Estadístico t corregido por heterocedasticidad y autocorrelaci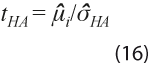ón: con 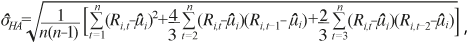sirve para probar la hipótesis nula de que la media de las revisiones es 0 y tiene distribución asintótica normal estándar. La desviación estándar estimada incluye corrección de Newey y West (1987).
• Sesgo condicional: 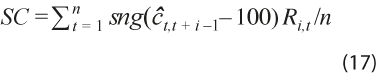con sgn(.) la función signo, asigna signo positivo a las revisiones por arriba de la tendencia y signo negativo a las revisiones por debajo de ella, así que valores positivos indican sesgo hacia la tendencia y negativos indican que las revisiones se alejan de ella.
• Autocorrelación de las revisiones: 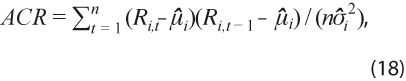indica existencia de información desaprovechada en las revisiones pasadas, por lo cual un método con valores de ACR alejados de 0 se considera ineficiente.

(C) Señal contenida en el ciclo:

• Cambio de signo: 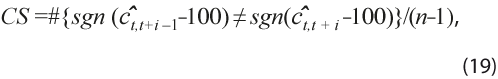con #{.} el número de elementos del conjunto, es la fracción que determina las fases del ciclo, ya que cuenta las veces que la revisión de la estimación cambia de abajo hacia arriba de la tendencia y cuántas veces a la inversa.
• Cambio de dirección: es la fracción del número de veces que el ciclo cambia de creciente a decreciente, y lo mismo en sentido contrario.

Resumen numérico de las revisiones

Las medidas del bloque (A) tienen las mismas unidades que las propias revisiones, por lo que están en el intervalo [0, ∞) y, mientras más cercanas a 0 sean, es mejor el comportamiento de las revisiones. Del bloque (B), las de (15), (16) y (17) toman valores en (− ∞, ∞ ), en tanto que (18) se encuentra dentro de (-1, 1) y, de nuevo, cuanto más cercanas a 0 sean, el método es mejor. Por último, los estadísticos (19) y (20) son fracciones dentro del intervalo (0, 1). Usualmente se presentan todas estas medidas numéricas de forma gráfica para cada uno de los métodos en consideración, ya que así se visualiza el comportamiento global de las revisiones para cada una de las medidas. Sin embargo, esta comparación es subjetiva, porque se basa en la apreciación visual de las gráficas de los estadísticos al paso del tiempo, como se hace en Guerrero (2013). De manera complementaria, se realiza el resumen numérico para decidir más específicamente cuál de los métodos es mejor. Para la comparación numérica se utiliza la mediana de los estadísticos (12) a (14) estandarizados —divididos entre sus desviaciones estándar muestrales— con el fin de evitar la influencia de su diferente variabilidad. Los estadísticos estandarizados permiten una comparación más objetiva, y en lo que sigue se mostrará una manera de resumirlos.

El estadístico t_HA indica significancia estadística de RM cuando sus valores se encuentran fuera del intervalo (-2, 2); es decir, si el valor de t_HA para una cosecha es menor en valor absoluto que 2, entonces el de RM se considera igual a 0 y no existe sesgo en la revisión, por lo tanto, conviene solo considerar los valores de RM que sean significativamente distintos de 0 para hacer un promedio de los que tienen sesgo positivo, RM(+), y otro promedio para el negativo, RM(-), por separado. De igual forma, se considera el estadístico SC, para el cual se requiere de un indicador semejante a t_HA y, por ello, se usa la desviación estándar muestral de SC calculada como la σ_HA de (16), de manera que se puede asignar significancia a los valores de SC; o sea, si el que corresponde al SC estandarizado está fuera de (-2, 2), se considera significativamente diferente de 0 y se usa para calcular uno de los dos promedios de valores SC, el de positivos SC(+) o el de negativos, SC(-). De esta forma, los estadísticos (15) a (17) se resumen mediante dos promedios para RM y otros dos para SC, que producen dos estimaciones del sesgo de las revisiones en términos relativos. Esto es, se calculan los valores de sesgo estandarizado [RM (+) + RM (−)] /[RM (+) − RM (−)] y [SC(+) + SC(−)] /[SC(+) − SC(−)], que se suman para obtener un solo valor del sesgo estandarizado, el cual se define como:

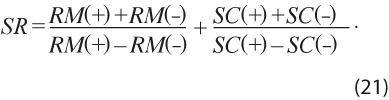Los datos de los estadísticos (18), (19) y (20) son de naturaleza distinta a los anteriores y es preferible analizarlos por separado. En específico, el estadístico ACR debe ser cercano a 0 para considerar adecuado el método. Por ello, se sugiere resumir a ACR con la mediana de los valores que toma con las diferentes cosechas de datos, mientras que CS y CD surgen de conteos que idealmente deberían ser 0 y tan solo se puede saber en cuántos casos y de qué tamaño es la fracción de veces que son distintos de 0. Así que la manera de resumir a estos dos estadísticos es mediante el valor del número de casos (conteo denotado con el símbolo #) y el promedio de las fracciones distintas de 0 (prom).

Evaluación de los ciclos: puntos de giro

La tarea final para seleccionar un método como preferible para el cálculo de los indicadores compuestos consiste en validar el desempeño cíclico de cada una de las variables en consideración respecto a los puntos de giro (crestas y valles) de la serie de referencia. Para ello, se usan herramientas estadísticas que califican: (i) conformidad cíclica entre las variables en estudio y la de referencia, de manera que no se omitan ni se detecten ciclos adicionales a los de la serie de referencia, con el fin de brindar credibilidad a la detección de puntos de giro y evitar señales falsas y (ii) longitud y consistencia del adelanto medido en meses, donde la longitud se mide con la media de los adelantos y el error estándar del adelanto medio es una medida de su consistencia. Asimismo, el valor más alto de la función de correlación cruzada (FCC) entre la serie en consideración y la de referencia indica el tiempo aproximado del adelanto promedio. Un indicador es adelantado si brinda información confiable de los próximos puntos de giro y de la evolución de la serie de referencia; para ello, su adelanto promedio debe ser parecido al del pico más alto de la FCC.

El paquete de cómputo que la OCDE pone a disposición de los analistas se denomina Análisis de los Ciclos del Sistema de Indicadores Compuestos (CACIS, por sus siglas en inglés), y sirve para verificar la validez de los puntos de giro detectados mediante el uso de un algoritmo conocido como Bry-Boschan. Para aplicarlo, se definen: a) el lapso mínimo entre una cresta y un valle (para el SIC es nueve meses); b) la longitud mínima de un ciclo, o sea, la distancia mínima entre dos crestas o dos valles (21 meses en el SIC); y c) un intervalo dentro del cual el punto de inflexión es mínimo o máximo (ocho meses en el SIC), es decir, el mes en el que un indicador alcanza un valor mayor que el de los ocho meses anteriores y de los ocho meses posteriores se considera como fecha tentativa de una cresta y, análogamente, para la de un valle.

Cuando un valle se mantiene durante varios meses, se escoge el último mes como el del cambio, y si se identifican dos o más se elige el de valor más bajo; a la inversa se hace con las crestas; lo importante es que unas y otros se alternen. Adicionalmente, en el caso de los indicadores del ciclo de crecimiento del SIC, en México se usa el procedimiento de Bry-Boschan simplificado, ya que al aplicar el filtro HP doble se producen ciclos suavizados. Por ello, es suficiente con localizar de manera secuencial las crestas y los valles de la serie, de forma que se satisfagan las restricciones mencionadas de longitud entre dos puntos de giro y entre ciclos.

Evaluación del ciclo del IC y del IA

Con el fin de tener en cuenta la incertidumbre asociada con la estimación del ciclo para los estimadores compuestos IC e IA, se propone calcular la varianza de cada uno de ellos y obtener entonces bandas de tolerancia de dos y tres errores estándar alrededor de su respectiva tendencia de largo plazo (ubicada en el valor 100). Para ello, se utiliza el hecho de que la serie de cada uno de esos indicadores tiene media constante (por la forma en que se construyen, el valor medio de largo plazo es 100) y su varianza es también una constante. Ésta se calcula con la siguiente expresión, que incluye la corrección por heterocedasticidad y autocorrelación propuesta por Newey y West (1987), o sea:

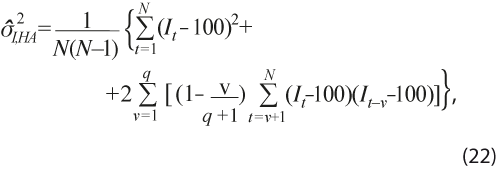donde I_t representa el indicador compuesto respectivo en el mes t y se elige el valor q = [0.75N^1/3], con [.] la función valor entero, para tener en cuenta la posibilidad de autocorrelación de orden superior a 1 en la serie del indicador.

Al igual que con la propuesta para calcular la banda de tolerancia alrededor del componente de tendencia obtenido con el filtro HP, ahora se calculan intervalos de ±k errores estándar en torno de la tendencia de largo plazo del IC y del IA como , con el error estándar estimado del indicador respectivo, para cada t = 1, …, N. De nuevo se aplica el Teorema de Tchebysheff para afirmar que, en cada momento de observación t, se cumple:

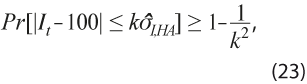donde k se elige igual a 2 para alcanzar una probabilidad mínima de 0.75 o como 3 para incrementar dicha probabilidad a 0.89.

Modelos de factores dinámicos (MFD)

Éstos se usan con la intención de reducir la dimensión de un grupo de series de tiempo correlacionadas a través de la extracción de factores subyacentes en ellas. En el análisis estadístico de fenómenos económicos, un MFD fue introducido por Geweke (1977), quien extrajo factores no-observables de un conjunto de variables del sector manufacturero. En la actualidad, estos modelos se emplean para pronosticar variables económicas de coyuntura, así como para realizar análisis de política económica. De hecho, se utilizan para construir indicadores compuestos con el fin de analizar relaciones entre variables subyacentes y específicas; también se emplean los factores resultantes como variables instrumentales, entre otros usos que se les puede dar en la práctica.

Además, los MFD se han popularizado debido a que los bancos de información económica han incrementado sus datos disponibles, tanto en número de series de tiempo como en la frecuencia de las observaciones que contienen, lo cual hace que la reducción de dimensión sea un tema de actualidad. Para más detalles acerca de estos modelos, se sugiere consultar la revisión realizada por Bai y Ng (2008).

El modelo El MFD, para cada momento de observación t = 1, …, N, se expresa como:

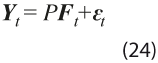con

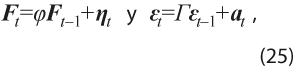donde los vectores Y_t= (Y_1t , … , Y_kt)ʼ y ε_t = (ε_1t , … , ε_kt)ʼ son de dimensión k x 1. Los factores comunes no-observables F_t= (F_1t , … , F_rt)ʼ y el componente idiosincrático ε_t , siguen procesos de tipo vector autorregresivo de orden 1 en el presente caso, de acuerdo con Corona et al. (2017). Éstos explican la evolución del grupo de series de tiempo Y_t , mientras que el componente idiosincrático tiene efectos sobre cada serie de manera individual. Los factores y el vector de errores aleatorios de media 0, η_t , son de tamaño r × 1, con r < k. La matriz de cargas de los factores P = (p₁ , …, p_k )’ es de dimensión k × r, en tanto que ᵠ y Г son de dimensión r × r y k × k, respectivamente, y cumplen las condiciones que garantizan la estacionariedad de los procesos a los que están asociadas (ver Lütkepohl, 2005).

Se define ahora la matriz de varianza-covarianza de los errores del factor como una matriz diagonal ∑_ƞ que tiene elementos ordenados en forma descendente, o sea, σ_ii>σ_jj>0 para i < j. Por su lado, los ruidos idiosincráticos se suponen no-correlacionados con las innovaciones de los factores para cada uno de los adelantos y rezagos, de tal forma que E(ε_t ηʼ_t-h)= 0 para toda h. Además, el vector de errores a_t es de dimensión k × 1 y se comporta como ruido blanco con matriz de varianza-covarianza ∑_a positiva definida.

Estimación de cargas y factores

Para estimar P y F_t , se deben imponer restricciones de identificabilidad y en el contexto de componentes principales (CP) —ver Stock y Watson (2002)— se suele imponer la restricción P’P = kI_r y FF’ diagonal, donde F = (F₁ , …, F_N) es una matriz r x N. De esta forma, se plantea el problema de minimización cuadrática:

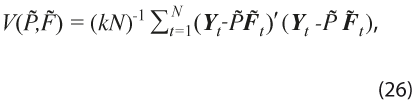donde, hipotéticamente, los verdaderos factores y matriz de cargas son y . Entonces, al definir Y= (Y₁, … , Y_N)ʹ como una matriz N×k, la solución de CP equivale a fijar como veces los vectores propios asociados a los primeros r valores propios de la matriz Y’Y. Consecuentemente, el estimador de los factores que se obtiene por CP está dado por:

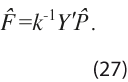Si el componente idiosincrático está débilmente correlacionado entre variables, aunque sea autocorrelacionado y heterocedástico, los estimadores y convergen a las verdaderas matrices P y F cuando k y N tienden al infinito, como lo demostró Bai (2003). De esta forma, los estimadores y se utilizan debido a su flexibilidad y porque requieren de pocos supuestos para brindar estimaciones consistentes. Para refinar el estimador dado por la expresión (27), sobre todo en el caso de muestras pequeñas, Doz et al. (2011) propusieron reestimar la matriz F en una segunda etapa a través del suavizamiento de Kalman, en el supuesto de que su correspondiente dinámica esté dada por la expresión (25). Específicamente en el caso de muestras pequeñas, Poncela y Ruiz (2016) muestran que el estimador en dos etapas proporciona estimaciones más cercanas al verdadero factor que el obtenido al aplicar solo CP. En este trabajo, dado que el número de series de tiempo es pequeño, tanto para IC como para IA, se considera apropiado emplear el procedimiento en dos etapas, es decir, CP con suavizamiento de Kalman; cabe notar que éste consiste en estimar los valores pasados de los factores, dada toda la información disponible en la muestra; esto es contrario a lo que ocurre con la predicción, donde se estiman valores futuros al último dato observado, o con el proceso de filtrado, en el que se estima el valor para t dada la información disponible hasta el tiempo t – 1.

Aplicación para estimar el IC y el IA

Debido a que el presente trabajo busca actualizar el SIC de México, los resultados de la aplicación del modelo de factores dinámicos se tratarán como un complemento de la estimación que surge con el enfoque de la OCDE; es decir, lo esperable es que sean parecidos a los que produce la metodología de la OCDE, ya que en las dos situaciones se busca la combinación óptima de fuentes de información acerca de una variable latente, el estado de la economía para la OCDE, que es común a todas las variables que componen al IC. Por ello, se propone combinar los índices que surgen de las dos metodologías, de manera que se aproveche al máximo la información disponible pues, aunque en ambos casos se usan los mismos componentes, la forma de agregar su información es distinta y esto es lo que se desea aprovechar con la combinación de los dos índices: reducir la incertidumbre en la estimación para ver con más claridad el patrón cíclico.

Para que la combinación sea válida, los dos métodos deberían proporcionar indicadores que en términos estadísticos estimen lo mismo. Esto debe ser verificado mediante la validación de: 1) que los dos índices carezcan de tendencia, es decir, que sean estacionarios en nivel, para lo cual se usa una prueba de raíces unitarias del tipo Dickey-Fuller aumentada y 2) que fluctúen alrededor del mismo valor medio, ubicado en 100, que representa la tendencia de largo plazo para ambos índices. Esto se valida con una prueba tipo t, con corrección de la varianza estimada por heterocedasticidad y autocorrelación.

Una vez validadas las condiciones anteriores, se combinan los dos índices mediante un promedio ponderado que tenga en cuenta su variabilidad y covarianza. Las ponderaciones asociadas a cada uno de los índices, I_1t con varianza σ²₁ e I_2t con varianza σ²₂, y con covarianza contemporánea σ₁₂ , se obtienen al resolver el siguiente problema que busca el valor de la ponderación c en la expresión:

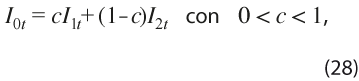de forma tal que minimice la varianza del índice combinado, la cual está dada por:

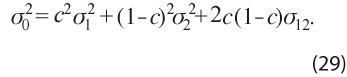Para lograr esto, se deriva esta expresión respecto a c, se iguala a 0 y se resuelve la ecuación resultante, con lo que se llega a:

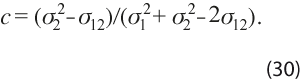Por consiguiente, el índice que combina óptimamente a los dos índices, en el sentido de varianza mínima, es:

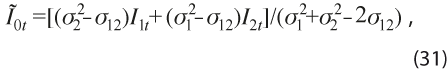
el cual tiene la misma media que I_1t e I_2t y menor varianza que los índices individuales.

Aplicación empírica

Las series que se tuvieron en cuenta en este trabajo son las seis que forman el IC: IGAE, IAI, IISBS, ATPIMSS, TDU e IT. Las seis del IA: TEM, CSAAM, PONMB, TCR bilateral, TIIE e ISP500.

Se contempló la posibilidad de que alguna otra serie surgiera como indicador viable para integrar el IC o IA, por lo que se tuvieron en cuenta seis variables adicionales: horas-hombre trabajadas en la manufactura (HHMAN), índice de confianza del consumidor (ICC), producción de vehículos automotores (PROD_VA), índice de volumen físico de la construcción (CONS), precio promedio del petróleo crudo exportado (PPET) y base monetaria real (BMR). Éstas se eligieron por su representatividad de alguno de los bloques económicos definidos en el taller del SIC realizado en septiembre del 2014. Esto es, que fueran indicadores de: 1) demanda, 2) empleo y mercado laboral, 3) manufactura, 4) opinión, 5) sector externo y 6) monetario o financiero. Dicho criterio teórico se complementó con el empírico de que las series iniciaran, al menos, en enero del 2004.

Las series utilizadas tienen distinto mes inicial, pero para este trabajo todas terminan en noviembre del 2016. Los resultados numéricos fueron obtenidos, en buena medida, con los programas de cómputo disponibles en el área del INEGI encargada de dar mantenimiento al SIC, aunque hubo necesidad de modificar algunos de ellos para los fines específicos de esta investigación.

En este apartado se muestran los resultados que surgen al aplicar las técnicas de análisis a un par de series, IGAE y TDU. Los resultados de las aplicaciones a las otras 16 series se muestran en el reporte técnico de Guerrero y Corona (2017). En principio, se presentan los resultados del cálculo y respectivo análisis para decidir entre diferentes opciones de paso de banda para las frecuencias del ciclo: HP(12,120), HP(12,96) y HP(12,72), que corresponden a ciclos de entre uno y 10 años en el primer caso, entre uno y ocho en el segundo y entre uno y seis en el tercero. La primera opción es la que se usa en el INEGI, la tercera surge de la creencia generalizada de que en México los ciclos son sexenales (e. g., Heath, 2000) y la segunda se consideró por ser intermedia entre las otras dos. El número de cosechas de datos por generar se fijó como la mitad de los datos de la serie en estudio, es decir, 50% de los del inicio de la serie fueron elegidos para realizar la estimación inicial del ciclo y el restante, para efectuar las revisiones.

Análisis de las revisiones

Ya que las primeras se realizan con menos datos que las subsecuentes —y por ende son muy inestables—, se dejó fuera de los cálculos a 20% de las revisiones iniciales. Asimismo, al final de la serie de cosechas hay mucha inestabilidad y, por ello, se decidió también eliminar 10% de éstas.

Las gráficas de las figuras 2 y 3 para el IGAE y la TDU presentan los diferentes estadísticos a lo largo de las cosechas de datos recortadas. En éstas, el eje horizontal indica las cosechas de datos y el vertical, los valores de los estadísticos respectivos. Las líneas de color negro corresponden al filtro HP(12,120); las rojas, al HP(12,96); y las verdes, al HP(12,72). Una característica que debe subrayarse es que el efecto del cambio de filtro no es lineal, de manera que aun cuando el HP(12,96) es intermedio entre los otros dos, su comportamiento en las revisiones no es necesariamente un efecto promedio de las revisiones de los otros filtros. No obstante, el valor de algunos estadísticos del HP(12,96), como los referidos al tamaño de las revisiones, sí tiende a encontrarse entre los valores de las revisiones obtenidas con los filtros HP(12,120) y HP(12,72).

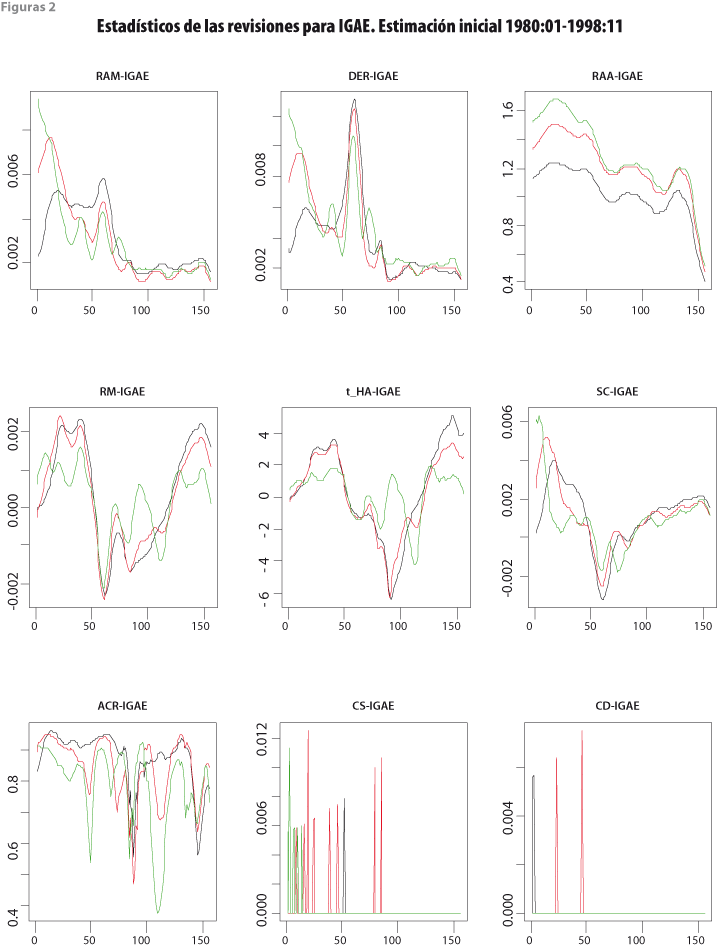
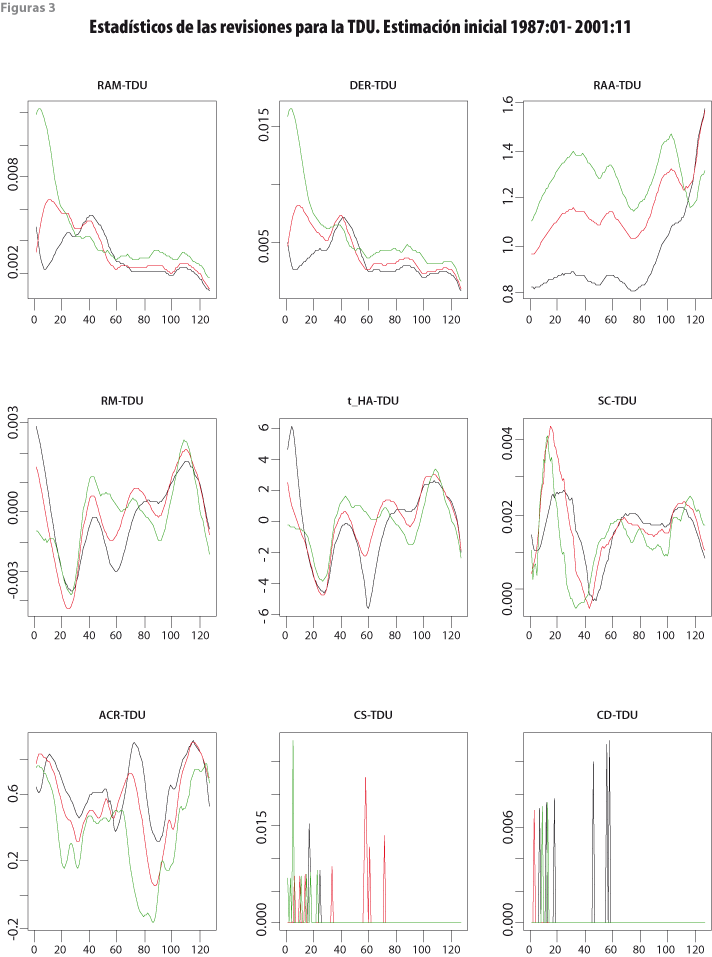
Los resultados de las revisiones pueden compararse con el resumen de los estadísticos (12) a (17), según se muestra en el cuadro 1 para el IGAE y en el cuadro 2 para la TDU. Con el fin de asignar calificaciones a los resúmenes estadísticos en una escala del 1 al 3, donde 3 es mejor, se tuvo en cuenta la siguiente guía: (i) respecto al promedio de las medianas del bloque (A), si el mayor promedio difiere en 5% o más del que le sigue, se asigna calificación más alta al promedio de medianas más pequeño y, si no hay tal diferencia, se asigna la misma calificación a los dos promedios; (ii) las medidas de sesgo se evalúan de manera conjunta para RM y para SC, por lo que se usa el sesgo relativo SR definido por (21) que, mientras más pequeño sea, es mejor, y de nuevo se asigna la calificación en función del valor de SR y se consideran solo las diferencias relativas de al menos 5% —sin considerar signo—; y (iii) el estadístico ACR se resume con la mediana de los valores de las autocorrelaciones, y su puntaje se obtiene con una regla semejante a las usadas en (i) y (ii), esto es, si la mediana más grande difiere en 5% o más de la que le sigue en magnitud, se asigna calificación más baja a la mayor mediana ACR, y este criterio se aplica por parejas al comparar los valores del estadístico. El cuadro 1 muestra que el filtro HP(12,72) brinda mejores resultados para el IGAE y el cuadro 2 indica que HP(12,96) es preferible para la TDU.

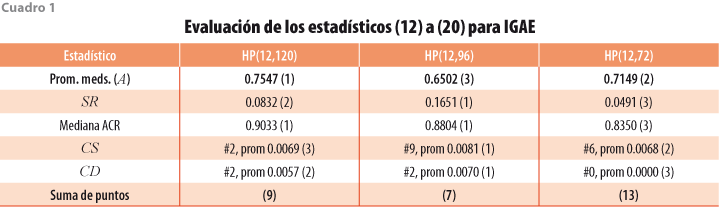
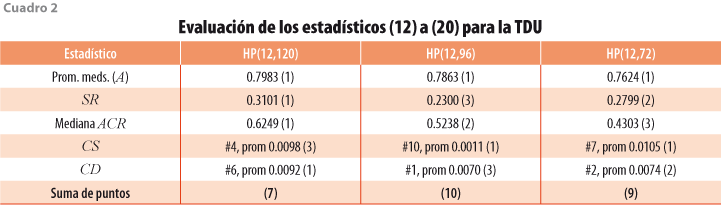
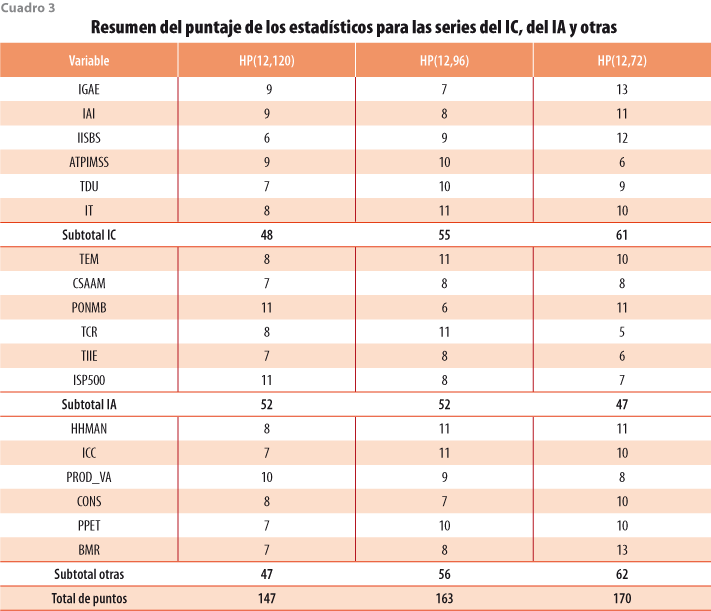
El resumen general para todas las series en estudio se presenta en el cuadro 3, donde se aprecia que el mejor método para los indicadores del IC es HP(12,72), mientras que para los del IA son aceptables tanto HP(12,120) como HP(12,96) y para los otros es HP(12,72). De esta manera, aunque no se obtiene una decisión unánime para todos los indicadores, resulta preferible usar HP(12,72) y en segundo lugar, HP(12,96).

Análisis gráfico de los puntos de giro

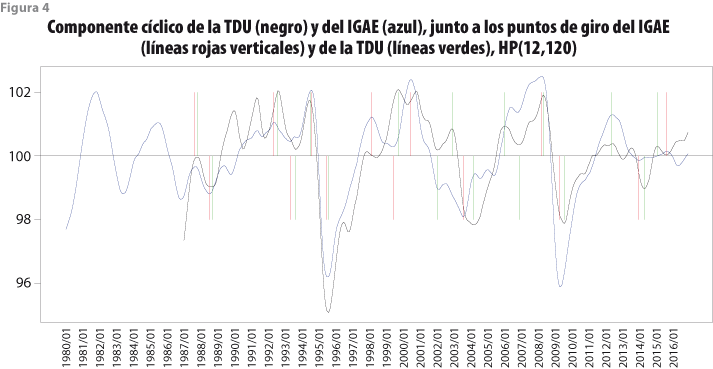
Los resultados anteriores conducen a proponer el método HP(12,72) como el más adecuado para la estimación del ciclo, ya que produce revisiones más estables del ciclo estimado. No obstante, se debe revisar el comportamiento de los indicadores para detectar los puntos de giro, de acuerdo con la serie de referencia. Esto se realiza con el paquete de cómputo CACIS, con el que se generan las gráficas de las figuras 4, 5 y 6, donde se observa el ciclo de este indicador y se comparan los puntos de giro del IGAE y de la misma TDU, las cuales permiten comparar los puntos de giro detectados por el algoritmo con respecto a los que se hayan determinado para la serie de referencia. Con ello se detectan ciclos omitidos o adicionales en el ciclo estimado de la TDU.

La figura 4 corresponde al filtro HP(12,120) y ahí se observa, a simple vista, que la sincronía de los ciclos de las dos series es buena, pero algunos puntos de giro son omitidos (líneas rojas de los meses 1998:06 y 1999:03). También, hay puntos de giro que la TDU detecta en forma adicional (líneas verdes de los meses 2002:02, 2002:12, 2006:01 y 2006:12). Esto es preferible cuantificarlo y presentarlo en forma resumida, como se muestra más adelante.

 

La figura 5 presenta los resultados para el filtro HP(12,96) y también muestra buena sincronía de los ciclos de las dos series, pero en más detalle se aprecia un punto de giro omitido (línea roja de 2000:07) y cinco adicionales (líneas verdes de 1999:09, 2002:01, 2002:12, 2006:01 y 2006:12).

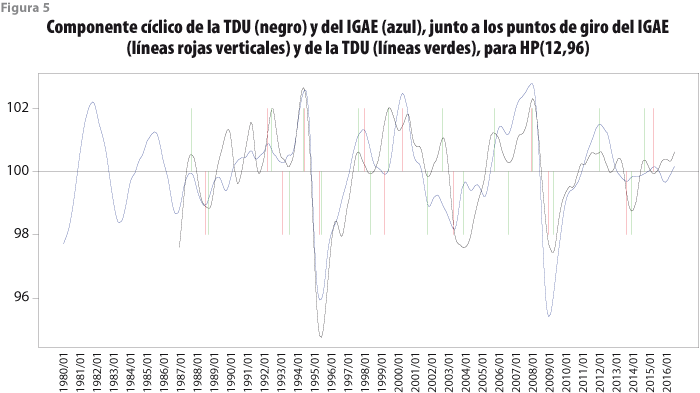
Por su lado, la figura 6 corresponde al filtro HP(12,72), en la cual también se observa que los ciclos de las dos series se encuentran bien sincronizados, aunque se aprecia un punto de giro omitido en 2000:07, así como siete adicionales en los meses 1990:01, 1991:11, 1999:09, 2002:01, 2003:01, 2005:12 y 2007:01.

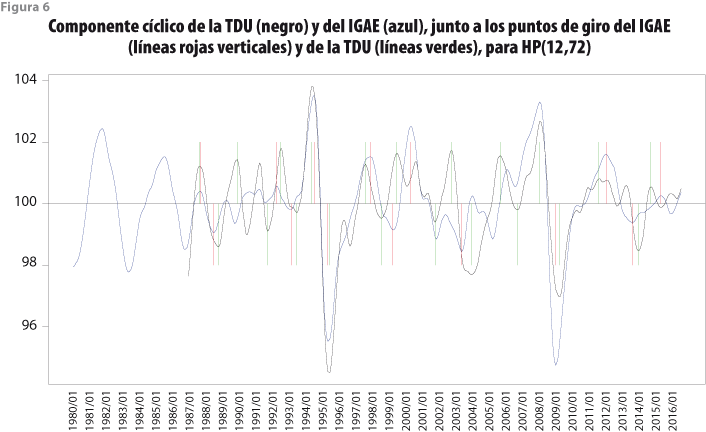
Análisis numérico de los puntos de giro

Otra herramienta estadística que interesa analizar es la FCC entre las distintas variables con la de referencia. Al considerar las tres opciones de filtro, con énfasis en la TDU, se observa un posible retraso del ciclo de la TDU respecto al del IGAE, pues las FCC para HP(12,120) y HP(12,96) tienen su pico más alto en -1. En contraste, el punto más elevado de la FCC con HP(12,72) se da en el retraso 0, lo cual brinda apoyo al uso de este método para extraer de la TDU información cíclica que sea compatible con la del IGAE. Asimismo, para cuantificar la concordancia de los puntos de giro entre un indicador y la serie de referencia se indican cuántos puntos de giro omite y cuántos adicionales detecta el patrón cíclico del indicador. Esta cuantificación se muestra en el cuadro 4 para la TDU, donde también se presenta el resultado de la medición de la longitud del adelanto respecto al IGAE y los valores de la FCC anteriormente comentados.

Los resultados del análisis de los puntos de giro presentados en el cuadro 5 para los demás indicadores en consideración mostraron que, en general, los métodos HP(12,120) y HP(12,96) hacen que los componentes del IC omitan más puntos de giro que el HP(12,72), excepto en el caso del IISBS. Asimismo, este último método se comporta de manera semejante a los otros dos al detectar puntos de giro adicionales. No obstante, el IC localiza uno más con HP(12,72) que con los otros dos filtros, lo cual no necesariamente es erróneo ni significa que este método extraiga señales espurias de los componentes del IC. En realidad, pudiera ser que los otros dos filtros no hayan revelado un punto de giro verdadero, que sí fue detectado por el HP(12,72).

Para el IA, el análisis que se realiza tiene como fin determinar el método que mejor adelante el patrón cíclico de la serie de referencia, de manera que solo se considera la longitud del adelanto mostrada en el cuadro 6 para las series que potencialmente servirían como adelantadas para el IC, como las del IA y las otras series. La longitud del adelanto es una herramienta que permite determinar el método, dentro de los tres considerados en este trabajo, que adelante el patrón cíclico del indicador que se considere coincidente y que al momento es el IGAE. Mientras no se haya decidido cuál es el IC que se va a utilizar, los resultados del cuadro 6 deben verse con cautela respecto a la longitud del adelanto y, por tal motivo, no se les da mayor relevancia por ahora.

Inclusión de nuevas variables

Como consecuencia del análisis previo, se determinó que el IC debe calcularse con el método HP(12,72), mientras que para el IA lo más natural es emplear el mismo filtro, de forma tal que los dos indicadores estén referidos al mismo paso de banda de las frecuencias cíclicas. Lo que falta es considerar la posibilidad de incluir alguno de los indicadores propuestos como adicionales, llamados otras series, o sustituir alguno de los indicadores que componen actualmente al IC y al IA. Las series potencialmente útiles para formar parte del IC son HHMAN y CONS, de acuerdo con la FCC del cuadro 6, pero CONS detecta muchos puntos de giro adicionales, lo cual condujo a desecharla. Al incorporar a HHMAN en forma adicional a las series componentes del IC actual, no se modificó la conformidad cíclica del IC y en la longitud del adelanto cambió el promedio de 0.5 a 0.3, mientras que el valor de la correlación en el pico 0 bajó de 0.93 a 0.92. Como no se observa una ventaja considerable respecto al IC actual, se prefirió no incluir a HHMAN.

De las cuatro variables restantes, ICC y PPET son potencialmente útiles como componentes del IA, de acuerdo con los resultados de la FCC en el cuadro 6, mientras que a la BMR se le descarta como posible componente del IC o del IA, ya que no es claro su patrón de adelanto y parece comportarse más como rezagada que como coincidente o adelantada. Sin embargo, estas comparaciones no son válidas, pues la comparación debe efectuarse con respecto al nuevo indicador coincidente que incorpora las mismas seis variables del IC, pero se calcula con el filtro HP(12,72) y será denotado como IC’ de aquí en adelante.

Lo anterior se presenta en el cuadro 7, donde se observa que las variables que forman el IC’ omiten algunos puntos de giro que captura el indicador compuesto y adicionan otros, pero esto es de esperar ya que tales variables no representan en sí mismas el estado de la economía, aunque sí forman parte de dicha variable no-observable. Además, en lo que toca al adelanto (o retraso) de las seis variables coincidentes, se aprecia que el promedio de adelanto se encuentra entre -0.2 y 1.7, lo que concuerda con los valores de los picos de la FCC, que van de -2 a 1, pero que no alcanzan el valor de ±3, que indicaría retraso o adelanto respecto al IC’, según se indica en OECD (2010, pp.10 y 31).

Por otro lado, en este cuadro también se aprecia que todas las variables que actualmente integran el IA son útiles para adelantar el comportamiento del IC’. De igual forma, se observa que tanto el ICC como el PPET son indicadores potencialmente útiles para ese fin. Desde luego, la conformidad cíclica no es buena, pero lo que importa es la longitud del adelanto y su consistencia. En ambos casos se obtienen adelantos mayores o iguales a tres meses, pero el ICC presenta inconsistencia entre adelanto promedio (6.7) y pico de la FCC (3), con alta desviación estándar (7.4), mientras que el PPET es más consistente en los valores que brinda para estos dos conceptos (4.6 vs. 3) y su desviación estándar es menor (6.2); sin embargo, la correlación en el pico más alto favorece al ICC (0.75) respecto al PPET (0.38). De esta forma, con los datos del cuadro 7 no es claro qué variable es preferible.

Para dilucidar qué variable debe ingresar, si acaso, al nuevo IA, se obtuvieron los resultados del cuadro 8, que consideran cuatro opciones: 1) mantener el IA con las seis variables que actualmente lo componen, 2) incorporar en forma adicional la variable ICC, 3) incorporar la variable adicional PPET y 4) incorporar tanto al ICC como al PPET. Los resultados de este ejercicio indican que es preferible incorporar solo al ICC, porque con ello se mantiene la consistencia entre adelanto promedio y pico de la FCC, con menor desviación estándar. Con estos resultados se tiene evidencia para modificar la estructura de componentes del IA, de forma que el nuevo indicador adelantado incluye al ICC y se denota como IA’.

Medición de la variabilidad del IC

Las franjas de tolerancia de ±2 y ±3 errores estándar para las variables IGAE y TDU usadas para ilustrar los resultados numéricos se muestran en las figuras 7 y 8. El patrón cíclico de la TDU es contrario al del estado de la economía, por lo que su componente cíclico se obtiene con el inverso de la variable TDU original. Figuras similares para las demás variables utilizadas en el cálculo del IC’ y del IA’ se presentan en Guerrero y Corona (2017). Debe notarse que en la gráfica de la parte superior de estas figuras aparece la tendencia estimada, junto con sus franjas de tolerancia, las cuales fueron calculadas con las expresiones (5) a (7).

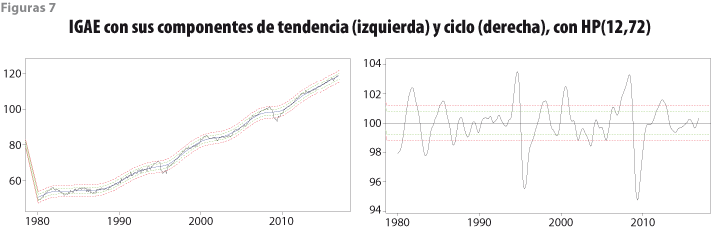
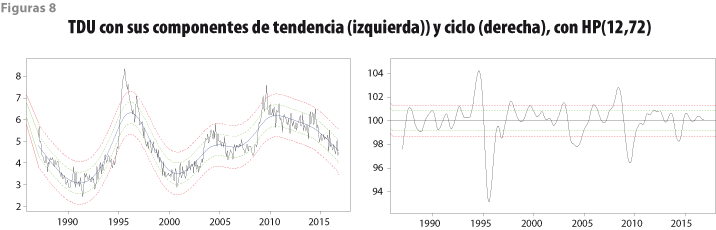
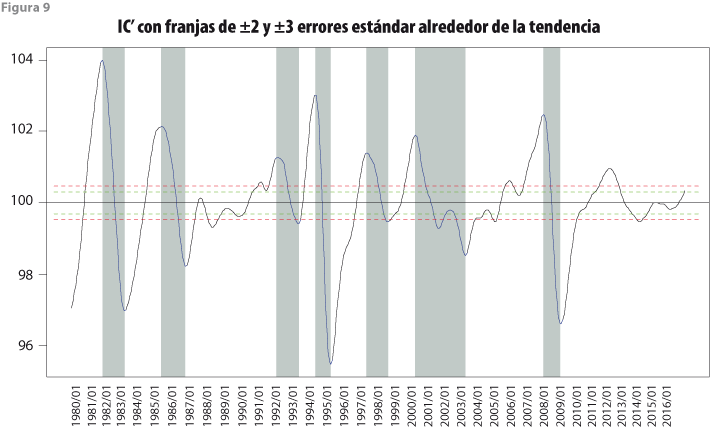
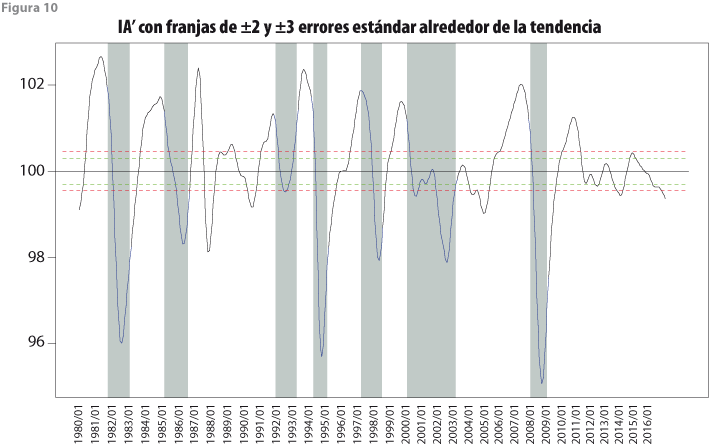
Para calcular las franjas de tolerancia alrededor de la tendencia de largo plazo de los indicadores IC’ e IA’, se usó la expresión (22) para con q = 5, porque el periodo en estudio cubre de enero de 1980 a noviembre del 2016, así que el número de meses es N = 443. Los resultados se muestran en la figura 9 para el IC’ y en la figura 10 para el IA’.

Fechado de crestas y valles

Con base en la franja de ±3 errores estándar se determinan fechas de crestas y valles razonablemente válidas —con probabilidad de, al menos, 0.89—, las cuales se presentan en el cuadro 9 para ambos indicadores, con el fin de realizar la comparación respectiva. La elección de un determinado mes como fecha de cresta o valle depende no solo de que el valor del indicador se salga de la franja de tres errores estándar, sino que, además, un valle sea precedido por una cresta, así como una cresta por un valle. De esta manera, una situación como la del IC’ en los meses 2000:09 a 2002:02 y 2002:10 a 2003:09 solo indica una cresta en 2000:09 y un valle en 2003:09, porque 2002:02, que tiene un valle válido, no va seguido de una cresta válida, pues 2002:10 no se sale de la franja de tres errores estándar. También, debe notarse que la cresta de 2012:05 no va seguida de un valle todavía, por lo cual no se cierra todavía un ciclo al final del periodo de observación.

Respecto al IA’, en el cuadro 9 también se observa que este indicador compuesto no reconoce la aparente cresta de 2004:03 y el aparente valle en 2005:05, ya que la cresta no alcanza a salir de la banda de tres errores estándar, aunque el valle sí lo haga, por lo cual solo se indica valle en el mes 2003:02 y cresta en 2007:10. Asimismo, se ve que el IA’ identifica dos crestas y dos valles válidos en los meses 1987:07, 1988:04, 1989:09 y 1991:02, que corresponderían a ciclos detectados en forma adelantada, pero que no tienen su contraparte en el IC’. Por último, al final de la serie se presenta una situación en la que hay un aparente valle en 2016:01, el cual correspondería a la cresta de 2011:02, pero esto no es totalmente válido, ya que la fase de recuperación no se alcanza a apreciar todavía.

En lo que toca a la mediana de los adelantos, en el trabajo de Guerrero (2013) fue 6, tanto para crestas como para valles, dejando fuera del cálculo un negativo de cresta y otro de valle. En cambio, ahora es 5.5 para crestas y 4 para valles, pero no se presentan valores negativos —que implicarían retraso en lugar de adelanto del IA’ respecto al IC’—, lo cual brinda más certeza al resultado de este trabajo. Otra comparación interesante es la de las fechas del cuadro 9 con las del SIC actual para los ciclos que pudieran considerarse oficiales, que son semejantes en la mayoría de los casos, aunque se excluyen algunas fechas, esto es, con datos a junio del 2017 para el IC y a julio del mismo año para el IA; en este cuadro se excluyen para el IC 1992:05- 1993:09 y 1997:10-1999:01, mientras que para el IA no se considera 1992:03-1992:12. De esta manera, de acuerdo con el SIC actual, solo hay cinco bandas verticales de ciclos oficiales para el IC, en tanto que en este trabajo se detectaron siete para el IC’, es decir, con el SIC actual del INEGI no se localizan las bandas verticales 3 y 5 que ahora aparecen en las figuras 10 y 11.

Resultados del MFD

En un primer ejercicio se estudió, tanto para las variables que forman el IC’ como para las del IA’, si un solo factor era estadísticamente apropiado. Dado que el número de variables no es grande, no se pueden utilizar los criterios tradicionales para determinar el número de factores, como el de Bai y Ng (2002) o el de Onatski (2010), que son válidos en el supuesto de muestras grandes.

Factor estimado coincidente

Primero se estudió el comportamiento de los valores propios de la matriz de varianza-covarianza muestral de las observaciones, denotada como , y se vio que un solo factor explica prácticamente el total de la variabilidad observada, es decir, para el IC’ se tuvieron los valores propios de , λ₁= 59995.91, λ₂= 2.19, λ₃= 0.83, λ₄= 0.45, λ₅= 0.34 y λ₆= 0.08, así que usar r = 1 es apropiado.

La figura 11 muestra el indicador IC’, el IC que calcula el INEGI —con datos a marzo de 2017—, del factor estimado en dos etapas , así como sus bandas de 95% de confianza y de la estimación combinada que se obtiene al ponderar con la constante , por lo que asigna menos peso a que al indicador IC’. Las bandas de confianza solo fueron estimadas para el periodo en que se cuenta con información de todas las variables que componen al IC’ (desde 1987:01). También se presentan las franjas de tolerancia de ±2 y ±3 errores estándar de la figura 9, alrededor del valor medio 100, que representa la tendencia de largo plazo del IC’. En la figura 11 se observa total concordancia entre los comportamientos de IC’ y del , mientras que el IC muestra un comportamiento distinto, particularmente al final del periodo de análisis, ya que no muestra efectos significativos del ciclo, en tanto que el IC’ y sí lo hacen.

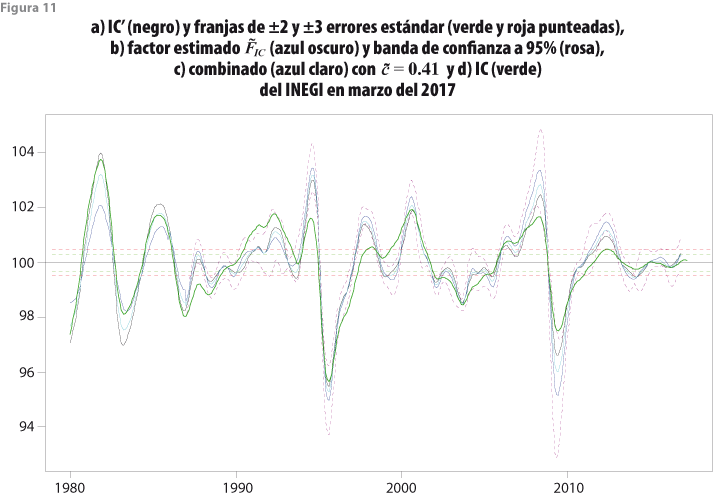De hecho, los indicadores IC’, y su combinación indican la misma conformidad cíclica y la banda de confianza de cubre en 86% de los casos al IC’. Por consiguiente, se puede concluir que al utilizar el método HP(12,72) o el MFD se obtienen prácticamente las mismas conclusiones, de donde es claro que la combinación también indica lo mismo que los indicadores considerados por separado. En contraste, el IC que actualmente genera el INEGI sí muestra un patrón distinto, en particular al final de la serie, aunque en general se encuentra dentro de la banda de confianza del 58% de las veces.

Es necesario verificar que el IC’ y no sean estadísticamente diferentes, para que a se le considere un indicador compuesto válido. Por ello, se verificó que la media de la serie de diferencias IC’– , corregida por autocorrelación, sea estadísticamente igual a 0, así como que la prueba de DFA conduzca a la conclusión de que el comportamiento es estacionario de segundo orden. En ambos casos, se obtienen los resultados deseados y el cuadro 10 los resume.

Factor estimado adelantado

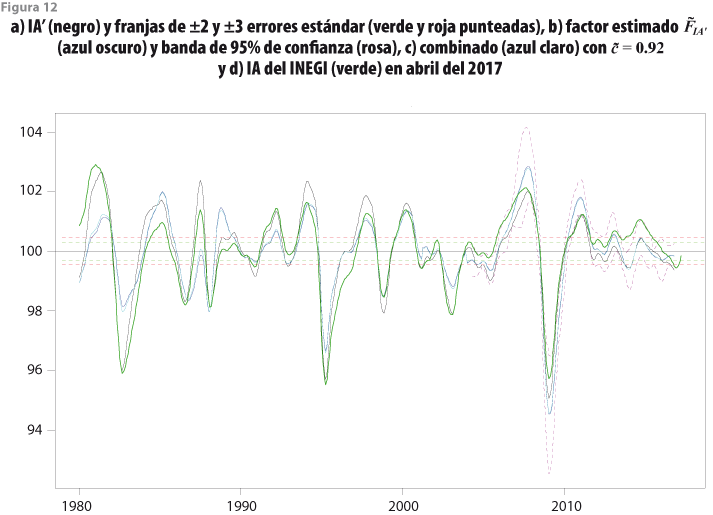
La figura 12 muestra la gráfica de los resultados obtenidos con el IA’, para el cual también se encontró que usar un solo factor es apropiado, pues con él se explica prácticamente el total de la variabilidad observada (los valores propios de la matriz de varianza-covarianza son λ₁=70044.04, λ₂=4.29, λ₃=1.31, λ₄=0.64, λ₅=0.38 , λ₆=0.28 y λ₇=0.06). En este caso se pueden apreciar ciertas discrepancias entre el IA’ y el , ya que el IA’ presenta crestas y valles más pronunciados entre 1980 y el 2005. Por otra parte, del 2005 en adelante, ambos indicadores muestran comportamientos similares, lo cual se nota con claridad en las bandas de confianza. En total, la banda de confianza de cubre 90% los valores del IA’, mientras que solo cubre 66% de los del IA del INEGI. Además, en este caso la ponderación tomó el valor , por lo que e resultaron ser muy similares. Así como sucedió con IC’ al compararlo con el IC del INEGI, ahora el IA’ tiende a señalar un ciclo al final del periodo de análisis que el IA del INEGI no detecta.

 

Es importante señalar que la combinación de indicadores, tanto del IC’ con el , como del IA’ con el , es óptima en términos estadísticos y, por ello, sería el indicador recomendado para utilizarse de manera rutinaria, de no ser porque la estimación de los factores dinámicos requiere que se cuiden varios detalles de la modelación involucrada, lo cual implicaría un mayor esfuerzo y dedicación de parte del personal encargado del mantenimiento del SIC en el INEGI, además de que no se obtiene una ganancia en explicación que amerite el trabajo adicional.

Igual que se hizo con el IC’, también se verificó que el IA’ y el no sean estadísticamente diferentes, con lo que se concluyó que la media de la diferencia IA’- es 0 y que su comportamiento es estacionario. En el cuadro 11 se presentan los resultados respectivos.

Como apoyo a la recomendación de cambiar los indicadores IC e IA del INEGI por el IC’ e IA’, las figuras 13 presenta gráficas por parejas de indicadores con el tiempo desfasado cinco meses en los indicadores coincidentes para visualizar la concordancia de movimientos. Al retrasar las variables IC e IC’para compararlas con sus respectivos indicadores adelantados, se pueden calcular las correlaciones entre parejas de variables; para el IC(-5) e IA la resultante es 0.80 y para el IC’(-5) e IA’ es 0.87, lo cual señala una mejoría en concordancia de movimientos. Además, visualmente se aprecia que los patrones de los indicadores propuestos son más compatibles entre sí que los de los otros dos indicadores, en especial al final del periodo de estudio, donde se observa un alejamiento entre los indicadores del INEGI, que no es tan marcado en los propuestos en este trabajo.

Conclusiones y recomendaciones

El trabajo que aquí se reporta se originó por la necesidad de actualizar el SIC que se mantiene en el INEGI con la idea de mejorar de alguna manera los resultados que surgen de dicho Sistema. Para ello, se probaron distintos métodos de filtrado del tipo HP doble para validar el método actualmente en uso en el INEGI y se hizo uso de las herramientas propuestas por la OCDE para comparar filtros alternativos que calculan tendencias y ciclos. Para el análisis de las revisiones del ciclo estimado, se diseñó un mecanismo estadístico que resume los resultados de las comparaciones de una manera más objetiva que la que comúnmente se usa. Se encontró que los indicadores presentan mejor conformidad cíclica al calcularlos con el filtro HP(12,72) y se decidió usarlo para calcular tanto el indicador coincidente como el adelantado, básicamente para mantener el mismo paso de banda de las frecuencias del ciclo en ambos indicadores.

Se consideró también la posibilidad de usar alguna variable adicional o sustituta de las 12 que actualmente se utilizan en el INEGI para construir los indicadores IC e IA que pudiera mejorar sus respectivos desempeños. Se encontró que el IC’ no requiere cambio de las variables empleadas en la actualidad, mientras que para el IA’ se determinó que sí es útil incluir al ICC como un componente adicional. Por otro lado, para distinguir lo que se puede considerar tendencia de lo que no lo es, se propusieron algunas técnicas estadísticas que conducen a lograr dicho objetivo. Con estas bandas se puede distinguir con más claridad, y basados en los datos disponibles, un efecto de carácter cíclico del de otro tipo que pudiera ser parte de la tendencia.

Este trabajo se orientó en el ciclo de crecimiento, que se aplica tanto en la OCDE como en el INEGI; no obstante, como en el INEGI también se usa el enfoque de ciclo clásico, conviene mencionar que a partir de los resultados aquí obtenidos se podría también realizar el cálculo de los respectivos indicadores que corresponden al enfoque de ciclo clásico, el cual no requiere de la cancelación de la tendencia y, por ello, lo que se podría hacer es, simplemente, restaurar la que se eliminó al momento de realizar los cálculos para generar los ciclos de crecimiento. Con esta operación se pueden regresar las series a sus niveles originales y hacer el análisis respectivo con éstas, a la manera clásica. Desde luego, éste es un ejercicio que convendría llevar a cabo como investigación futura para observar con detalle los patrones que se producen y obtener evidencia empírica que permita recomendar o no el uso de estos nuevos indicadores.

Adicionalmente, se empleó un MFD, que tiene una base de teoría estadística muy sólida para calcular los indicadores. Con este modelo se encontró que un solo factor es suficiente para capturar el comportamiento de las variables latentes asociadas con el estado de la economía y su adelanto respectivo, que es a lo que se refieren el IC’ y el IA’. El objetivo principal de utilizar el MFD fue complementar la información que brindan los indicadores IC’ e IA’, no sustituirlos, por lo cual se demostró que el IC’ y el factor respectivo son indistinguibles, en términos estadísticos, lo cual brinda sustento al cálculo que se realiza con el HP(12,72). Para el IA’, los resultados que produce este filtro y el factor son también muy parecidos, en especial al final del periodo muestral, donde se detecta el inicio de una posible fase de recuperación —la salida de un valle— que el IA del INEGI no alcanza a distinguir. Una manera de complementar los enfoques de la OCDE y del factor dinámico es mediante una combinación de los indicadores compuestos y los factores. Con ello se obtiene un promedio ponderado de los estimadores en los dos casos —coincidente y adelantado— con ponderación que da prioridad al IC’ en el primer caso y que desfavorece al IA’ en el segundo. Lo más relevante de haber aplicado esta técnica estadística radica en que sus resultados brindan apoyo al uso de los nuevos IC’ e IA’ y desacreditan al IC e IA.

Las recomendaciones que surgen de este trabajo son: 1) modificar el cálculo de los indicadores compuestos para utilizar ahora los indicadores IC’ e IA’; 2) tener en cuenta el nuevo fechado de ciclos —crestas y valles— para el nuevo IC’ que aquí se presenta, el cual surgió del análisis convencional que se realiza con el método de la OCDE, complementado por las bandas de tolerancia con las que se detectan comportamientos más cercanos a la tendencia que al ciclo; 3) regularizar la periodicidad de las actualizaciones, ya que del 2010 al 2014 fue necesario cambiar algunas variables componentes de los indicadores, mientras que del 2014 al 2017 fue pertinente modificar el método de estimación de la tendencia, así como incorporar algunas innovaciones de carácter metodológico-estadístico para mejorar la interpretación de los resultados. Por ello, sería apropiado no dejar pasar más de cuatro años entre una actualización del SIC y la siguiente, como ocurrió en las ocasiones anteriores, y estar alerta ante la posibilidad de que la actualización se requiera con mayor frecuencia debido a cambios en el entorno económico del país.

____

Fuentes

Anas, J. y L. Ferrara.“Detecting Cyclical Turning Points: The ABCD Approach and Two Probabilistic Indicators”, en: Journal of Business Cycle Measurement and Analysis. OECD Publishing, CIRET – 2, 2004, pp. 193-225.

Bai, J. “Inferential theory for factor models of large dimensions”, en: Econometrica, 71(1), 2003, pp. 135-171.

Bai, J. y S. Ng. “Determining the number of factors in approximate factor models”, en: Econometrica, 70(1), 2002, pp. 191-221.

___“Large dimensional factor analysis” en: Foundations and Trends in Econometrics, 3(2), 2008, pp. 89-163.

Bandholz, H. y M. Funke.“In Search of Leading Indicators of Economic Activity in Germany”, en: Journal of Forecasting, 22(4), 2003, pp. 277-297.

Corona, F., P. Poncela y E. Ruiz. “Determining the number of factors after stationary univariate transformations”, en: Empirical Economics, 53, 2017, pp. 351-372.

Di Fonzo, T. The OECD project on revision analysis. First elements for discussion. Paper prepared for the OECD Short-term Economic Statistics Expert Group. Paris, OECD, 2005.

Doz, C., D. Giannone y L. Reichlin. “A two-step estimator for large approximate dynamic factor models based on Kalman filtering”, en: Journal of Econometrics, 164(1), 2011, pp. 188-205.

Geweke, J.“The dynamic factor analysis of economic time series”, en: Aigner, D. J. y A. S. Goldberger (eds.). Latent Variables in Socio-Economic Models. Amsterdam, North-Holland, 1977.

Guerrero, V. M. “Time series smoothing by penalized least squares”, en: Statistics & Probability Letters, 77, 2007, pp. 1225-1234.

___“Estimating trends with percentage of smoothness chose the user”, en: International Statistical Review, 76(2), 2008, pp. 187-202.

___ “Capacidad predictiva de los índices cíclicos compuestos para los puntos de giro de la economía mexicana”, en: Economía Mexicana. Nueva época, XXII (1), 2013, pp. 47-99.

Guerrero, V. M. y F. Corona. Actualización del sistema de indicadores cíclicos de México. Reporte técnico. Ciudad de México, Dirección General Adjunta de Investigación, INEGI, 2017.

Heath, J. La maldición de los ciclos sexenales. Sucesiones presidenciales y crisis económicas en el México moderno. México, Grupo Editorial Iberoamericana, 2000.

Hodrick, R. J. y E. C. Prescott. “Postwar U.S. business cycles: An empirical investigation”, en: Journal of Money, Credit and Banking, 29, 1997, pp. 1-16.

INEGI. Metodología para la construcción del sistema de indicadores cíclicos. Aguascalientes, México, INEGI, 2015.

Lütkepohl, H. New Introduction to Multiple Time Series Analysis. Berlin, Germany, Springer-Verlag, 2005.

McElroy, T. “The error in business cycle estimates obtained from seasonally adjusted data”, en: Research Report Series – Statistics #2006-11. US Census Bureau, 2006.

Newey, W. y K. West. “A Simple Positive Semi-Definite, Heteroscedasticity and Autocorrelation Consistent Covariance Matrix”, en: Econometrica, 55, 1987, pp. 703-708.

Nilsson, R. y G. Gyomai. Cycle Extraction. A comparison of the Phase-Average Trend method, the Hodrick-Prescott and Christiano-Fitzgerald filters. Technical Report. Paris, OECD, 2008.

OECD. OECD Cyclical Analysis and Composite Indicators System (CACIS). USER’s GUIDE. Paris, OECD, 2010.

___OECD System of Composite Leading Indicators. Paris, OECD, 2012.

Onatski, A. “Determining the number of factors from empirical distribution of eigenvalues”, en: The Review of Economics and Statistics, 92(4), 2010, pp. 1004-1016.

Poncela, P. y E. Ruiz. “Small versus big data factor extraction in dynamic factor models: An empirical assessment in dynamic factor models”, en: Hilldebrand, E. y S. J. Koopman (eds.). Advances in Econometrics, 35, 2016, pp. 401-434.

Stock, J. H. y M. W. Watson. “Forecasting using principal components from a large number of predictors”, en: Journal of the American Statistical Association, 97(1), 2002, pp. 1169-1179.

Wackerly, D., W. Mendenhall III y R. L. Scheaffer. Mathematical Statistics with Applications. Sixth ed. Thomson/Brooks-Cole, 2002.