Niveles de marginación: una estrategia multivariada de clasificación

Edición: Vol.2 Núm.1 enero-abril 2011

Este documento plantea el uso de una estrategia de clasificación en el estudio de la marginación y del bienestar sustentada en un criterio propuesto para la búsqueda de las alternativas con mayor homogeneidad. Se parte de revisar el método de conglomeración según el grado de marginación, usado por el Consejo Nacional de Población (CONAPO), basada en la primera componente principal calculada a partir de las versiones estandarizadas de los indicadores seleccionados. La estrategia obtiene diversas clasificaciones con base en una o más de las componentes principales de los indicadores sin estandarizar, lo que resuelve las limitaciones identificadas. La mejor clasificación se determina usando el criterio propuesto. La aplicación de esta estrategia se ejemplifica con información municipal del II Conteo de Población 2005, también usada por el CONAPO. Se muestra que, para el ejemplo, la conglomeración óptima de municipios se alcanza cuando se usan las dos primeras componentes principales.   Palabras clave: clasificación, conglomeración, estratificación, componentes principales, marginación.		The use of a strategy for the classification of geographical units in the study of marginalization and well-being, supported by a proposed criterion for the search of more homogeneous alternatives, is introduced. The conglomeration method by degree of marginalization, used in Mexico by CONAPO, which is based on the first principal component computed from standardized versions of the selected indicators, is reviewed. In order to solve the identified limitations, the strategy whose use is being proposed obtains alternative classifications based on one or more principal components from the non-standardized indicators. The best classification is then determined using the proposed homogeneity criterion. The application of the strategy is exemplified using municipal information from the II Conteo de Población y Vivienda 2005, in Mexico as used by CONAPO. It is shown that, for this data, the optimal classification of municipalities is reached when only the first two principal components are used. Key words: Classification, clustering, stratification, principal components, marginality.

 

Nota: agradezco los comentarios del doctor Gerardo Leyva y de la maestra Miriam Romo, quienes contribuyeron a mejorar este trabajo.

Introducción

Hoy en día es frecuente escuchar que la implementación de tal o cual política pública, que busca atacar un problema de naturaleza multidimensional, ha sido basada en algún indicador compuesto o en alguna aplicación de éste. Sobra decir que un índice desarrollado de forma inadecuada puede limitar el efecto esperado de la aplicación de recursos fiscales (de montos casi siempre importantes) en la población a la que son dirigidos. Es por esta razón que se ha vuelto muy importante mejorar nuestra capacidad tanto para realizar los cálculos requeridos como para evaluar los resultados que así se obtengan. En general, los métodos para obtener indicadores compuestos han seguido siendo objeto de análisis y mejora; de cualquier modo, aún es frecuente encontrar indicadores de este tipo construidos mediante procedimientos y métodos más o menos rudimentarios.

Por su parte, en relación con nuestra capacidad para evaluar los resultados, hay —en general— ausencia de respuestas a la pregunta: ¿se puede medir de mejor manera lo que se quiere medir? Por ejemplo, en presencia de alguno de los indicadores de mayor uso actual para la ordenación de países o regiones (por ejemplo, el índice de desarrollo humano de la Organización de las Naciones Unidas), resulta difícil determinar si alguna modificación al valor del coeficiente de uno de los indicadores componentes mejora o empeora la descripción que el índice compuesto resultante hace del fenómeno en cuestión. En mi opinión, es claro que se requiere desarrollar la capacidad para medir, además, qué tan bien se mide lo que se desea medir.

La naturaleza multidimensional de los aspectos que se busca conocer trae consigo la dificultad adicional de comunicar los resultados alcanzados. Por esta razón se ha recurrido a procedimientos simples y fáciles de explicar. Por ello, llama la atención que el esfuerzo pionero del CONAPO (iniciado durante la primera mitad de la década de los 90 y basado en metodologías no tradicionales) haya encontrado buena aceptación y amplia aplicación. En efecto, el uso del análisis de componentes principales (ACP) como parte de la metodología permitió incorporar al análisis la covariabilidad de los indicadores utilizados, como lo exige un tratamiento formal del análisis de fenómenos multidimensionales o multivariados.

En relación con el análisis de componentes principales, la Organización para la Cooperación y el Desarrollo Económicos (OCDE) publicó en el 2005 un manual¹ para apoyar la elaboración de indicadores compuestos en el que se refiere al uso de esta técnica. Entre sus fortalezas, destaca su capacidad de resumir un conjunto de indicadores básicos en tanto se preserva la proporción máxima posible de la variación total en el archivo de datos original. Indica que las mayores ponderaciones son asignadas a los indicadores básicos que muestran la mayor variación entre países y destaca que ésta es una propiedad deseable para realizar comparaciones entre naciones, ya que los indicadores básicos que son parecidos entre ellas carecen de interés, pues no pueden explicar las diferencias en desempeño. En contrapartida, los autores del manual señalan entre las debilidades del método que las correlaciones no representan necesariamente la influencia real de los indicadores básicos en el fenómeno que está siendo medido; del mismo modo, indican que es sensible a modificaciones en los datos, así como a la presencia de observaciones aberrantes que pueden introducir variabilidad espuria.

Ya que a lo largo del texto se hará referencia a técnicas multivariadas de conglomeración (o clasificación o estratificación), conviene recordar otros esfuerzos encaminados a establecer clasificaciones socioeconómicas de áreas geográficas en México, desde el nivel de área geoestadística básica (AGEB) hasta el de entidad federativa. El Instituto Nacional de Estadística y Geografía (INEGI) desarrolló uno que, en sus orígenes, fue denominado niveles de bienestar; más adelante, el nombre fue cambiado por el de regiones socioeconómicas de México y es éste por el que aún se le identifica en el sitio de Internet del Instituto. Aunque este enfoque reconoce la naturaleza multidimensional del bienestar al incorporar un número importante de indicadores, el procedimiento estadístico de clasificación al que recurre (conocido como k-medias) basa la clasificación de una unidad en la distancia euclidiana entre ésta y los centroides de los conglomerados² , en otras palabras, no aprovecha la información relativa a las correlaciones entre los indicadores utilizados.

Al respecto, el ya citado manual de la OCDE señala que el análisis de conglomerados es otra herramienta para clasificar grandes cantidades de información en conjuntos más tratables, y ha sido también usado en el desarrollo de indicadores compuestos para agrupar información sobre países basada en su semejanza con base en diferentes indicadores básicos; además, sirve como: a) un método meramente estadístico de agregación de los indicadores; b) una herramienta de diagnóstico para explorar el impacto del uso de diversas metodologías durante la fase de construcción del indicador compuesto; c) un método para la diseminación de información sobre el indicador compuesto, sin perder la que se refiere a las dimensiones de los indicadores básicos y d) un método para seleccionar grupos de países para imputar datos faltantes con el propósito de reducir la varianza de los valores imputados.

El transcurso de casi dos décadas desde la aparición del primero de los estudios sobre el tema, así como la inminente realización del Censo de Población y Vivienda 2010, hacen necesaria la evaluación de la metodología y de sus resultados con el fin de elaborar una propuesta que incorpore desarrollos recientes y ayude a mejorar los efectos de su aplicación. Parece conveniente, en vista de lo que ya ha sido comentado, tomar como punto de partida en esta tarea la propuesta metodológica original. De este modo, la siguiente sección se ocupa de la descripción de la metodología hasta ahora utilizada; concluye con una visión crítica que pretende destacar algunos aspectos que, a nuestro juicio, merecen especial atención. La segunda sección plantea una metodología alternativa que atiende las limitaciones identificadas. Ambas son comparadas haciendo uso de la base de datos municipal que el CONAPO tiene disponible en su sitio de Internet, para el ejercicio del 2005. Los resultados numéricos se muestran en la tercera sección.

Cuando el número de variables es grande o se piensa que algunas de éstas no contribuyen a identificar la estructura de los conglomerados en el conjunto de datos, es posible llevar a cabo, de forma secuencial, la aplicación de modelos continuos y discretos; por ejemplo, diversos investigadores han realizado primero un análisis de componentes principales y, después, un algoritmo de conglomeración, usando los valores de las primeras componentes, lo que se ha dado en llamar análisis en tándem. Algunos de los resultados numéricos presentados en este trabajo se obtienen haciendo uso de este tipo de análisis, ya que se pretende hacer un esfuerzo por reducir la dimensión del problema en nuestra búsqueda por identificar una solución óptima. En consecuencia, se hace necesario proponer una medida que permita discernir cuáles son las mejores opciones; de esto se ocupa la cuarta sección.

A lo largo del documento, el uso de las metodologías discutidas será ejemplificado mediante su aplicación a la base de datos por municipio utilizada por el CONAPO.³ Mediante la aplicación del criterio desarrollado, se evalúa cada una de las alternativas de donde se pueden alcanzar algunas conclusiones y elaborar propuestas. Es posible destacar aquí tres resultados para estos datos:

Para la elaboración de esta nota, se ha decidido concentrarse en los aspectos meramente técnicos de los procedimientos de conglomeración. Las discusiones de carácter conceptual relativas a la conveniencia de incluir o no alguno de los temas o de los indicadores usados, o de la mayor influencia de uno en particular sobre resultados alcanzados pertenecen a trabajos de otra naturaleza. Con mayor razón, las implicaciones sociales, programáticas o presupuestales quedan fuera de los alcances de esta discusión, cuyo propósito principal es señalar y corregir las limitaciones de los procedimientos en uso.

Índice de marginación

 

De acuerdo con lo que señalan diversas publicaciones del CONAPO el “…índice de marginación es una medida-resumen que permite diferenciar entidades federativas y municipios según el impacto global de las carencias que padece la población, como resultado de la falta de acceso a la educación, la residencia en viviendas inadecuadas, la percepción de ingresos monetarios insuficientes y las relacionadas con la residencia en localidades pequeñas.

Así, el índice de marginación considera cuatro dimensiones estructurales de la marginación; identifica nueve formas de exclusión y mide su intensidad espacial como porcentaje de la población que no participa del disfrute de bienes y servicios esenciales para el desarrollo de sus capacidades básicas.

En el esquema 1.1 pueden verse las nueve formas de exclusión social de origen estructural que capta el índice de marginación, así como los indicadores utilizados.

Esquema 1.1

Esquema conceptual de la marginación^a

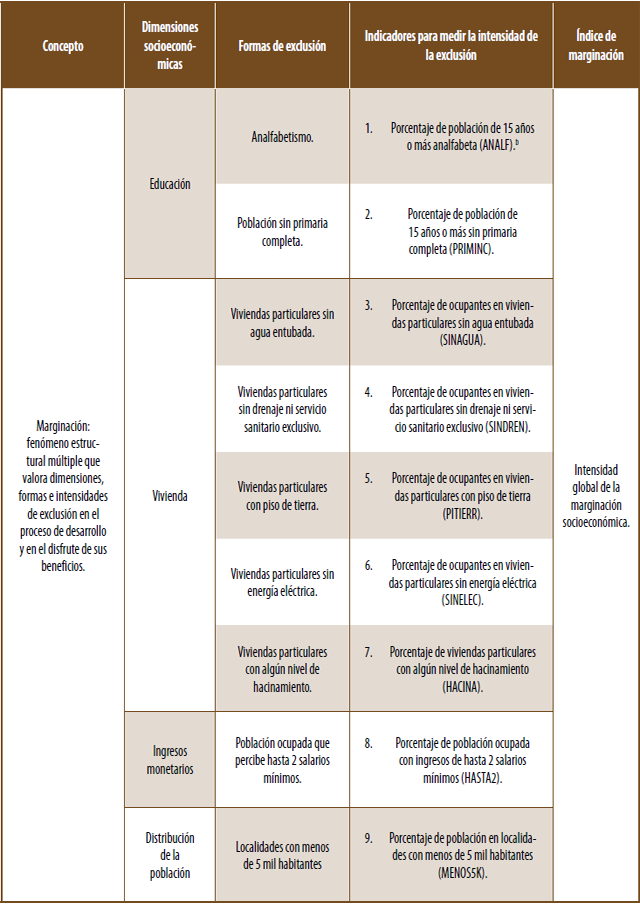
^a CONAPO (2004). Índice absoluto de marginación, 1990-2000. México, DF, recuperado en bit.ly/3zT7j7c

^b Mnemónicos a ser usados en este artículo entre paréntesis.

“Es importante señalar que para la estimación del índice de marginación se utilizaron como fuentes de información los resultados definitivos del II Conteo de Población y Vivienda 2005 y la Encuesta Nacional de Ocupación y Empleo (ENOE) correspondiente al cuarto trimestre del mismo año. El Conteo permite medir ocho de los nueve indicadores que integran el índice de marginación para las 32 entidades federativas y los 2 454 municipios del país existentes en el 2005, mientras que la ENOE proporciona la información sobre el nivel de ingresos de la población ocupada en las entidades federativas, a partir de la cual se estimó el indicador correspondiente a nivel municipal. Con ello se busca mantener al máximo la integridad del marco conceptual, las dimensiones, formas de exclusión e indicadores de los índices de marginación estimados por el CONAPO con base en los datos de los censos generales de Población y Vivienda de 1990 y 2000.”

La metodología estadística detrás del ejercicio índice de marginación del CONAPO, según se desprende del Anexo C. Metodología de estimación del índice de marginación, incluido en la citada publicación del 2006, tiene como objetivo el siguiente:

“Se busca generar un índice de marginación que evalúe el impacto global de las carencias y que cumpla, además, con ciertas características que faciliten el análisis de la expresión territorial de la marginación:

Aunque la publicación mencionada no lo explica como tal, los sucesivos ejercicios para el estudio de la marginación han buscado satisfacer un objetivo complementario. En efecto, el índice de marginación obtenido es usado como insumo en un procedimiento univariado para la conglomeración de las unidades geográficas consideradas, del cual se dice que es óptimo.⁴ Los cinco estratos resultantes se denominan como de muy alto, alto, medio, bajo y muy bajo grado de marginación. Con frecuencia, la elaboración y aplicación de programas públicos (tanto federales como estatales) hacen referencia a esta conglomeración más que a los valores mismos del índice. Ejemplo de lo señalado lo representan los siguientes programas:

Cada uno de los nueve porcentajes (indicadores del esquema 1.1) referidos arriba es calculado tomando en cuenta la población que no especificó encontrarse en la condición correspondiente. Tales cantidades son, además, estandarizadas lo que resulta de sustraer de cada uno de los valores el promedio nacional del indicador y de dividir la anterior diferencia entre la desviación estándar del indicador. En otras palabras, se calcula:

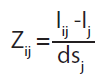(1)

donde:

Los indicadores estandarizados así obtenidos representan el insumo para una rutina estadística que obtiene las denominadas componentes principales. Esto es equivalente a usar la matriz de correlaciones como insumo para el ACP, la cual es un arreglo que resume la información relativa a la correlación entre indicadores. En vista de la estandarización, la varianza de cada uno de los indicadores será igual a 1 por lo que en la diagonal de la matriz de correlaciones ese valor se repetirá tantas veces como indicadores estén siendo considerados. Como se verá adelante, el hecho de que los valores de las varianzas de todos los indicadores sean iguales (y, en este caso, iguales a 1) puede contradecir el propósito del ACP que, entre otras cosas, busca establecer la dirección de máxima desigualdad, en general identificada con la primera componente principal.

De este modo, el índice de marginación adquiere la forma de una combinación lineal de los indicadores estandarizados:

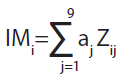(2)

donde:

Los autores del documento afirman que el “…índice de marginación así calculado corresponde a la primera componente del ACP. Puede demostrarse que la primera componente es la combinación de las variables originales que mejor resume, en un solo valor, la información del conjunto de los nueve indicadores…; para mayor precisión, vale la pena decir que la primera componente es la combinación de las variables cuya varianza es máxima. Se supone que es en este sentido que se dice que es la que mejor resume, en un solo valor, la información del conjunto de los nueve indicadores. La aplicación de la anterior metodología será ejemplificada a partir de los datos del Conteo 2005, así como de la ENOE del cuarto trimestre del mismo año, en que el CONAPO basó su índice de marginación municipal, 2005.⁵

El cuadro 2 muestra un resumen de los resultados de la aplicación del ACP a este conjunto de datos. Como podrá observarse, la varianza de la primera componente principal alcanza un valor apenas superior a 50% de la suma de las varianzas de los indicadores estandarizados, la que, en vista de la estandarización a que son sometidos los indicadores, coincide con el número de éstos.

Cuadro 1

Correlaciones entre los nueve indicadores básicos

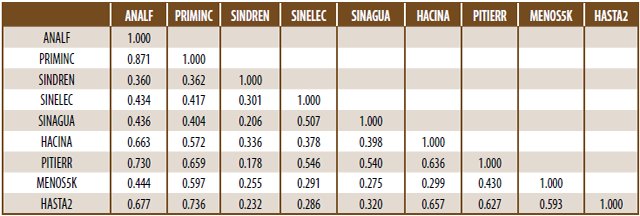
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

Cuadro 2

Valores propios de la matriz de correlaciones

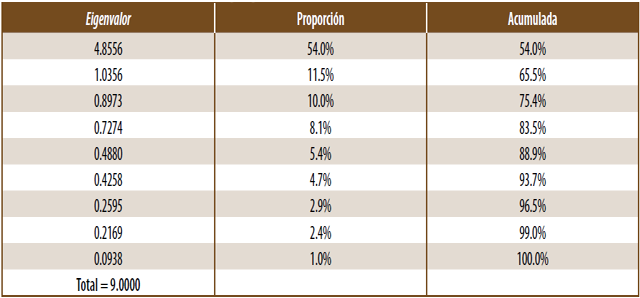
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

Aun cuando, en efecto, dicha componente principal representa el “mejor resumen individual de la información del conjunto de los nueve indicadores”, conviene preguntarse si tal resumen es suficientemente adecuado para los propósitos planteados; por ejemplo, es necesario considerar a las tres primeras componentes principales para lograr una explicación de la variabilidad total (suma de las varianzas de los indicadores insumo del ACP) superior a 75%, o hasta 6, para rebasar 90 por ciento.

El anterior resumen puede ser representado como se muestra en la gráfica 1. Si bien es clara la desproporción del valor del mayor valor propio o característico respecto al de cada uno de los otros, la suma de éstos casi iguala al de aquél. En otras palabras (y en términos de lo que en este contexto se entiende como explicación), basar cualesquiera conclusiones exclusivamente en la primera componente principal equivale a ignorar casi tanta información como la que se está aprovechando.

Gráfica 1

Valor acumulado de los valores propios obtenidos a partir del análisis de componentes principales de la matriz de correlaciones de los nueve indicadores básicos

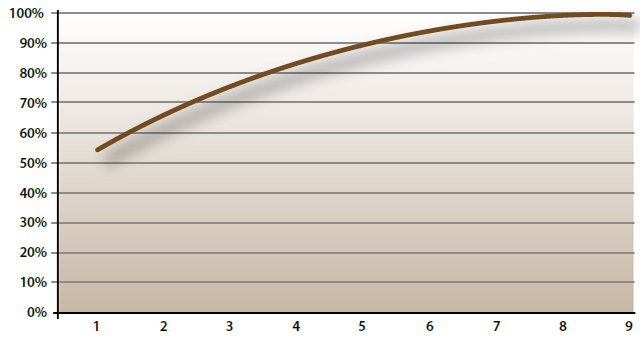
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

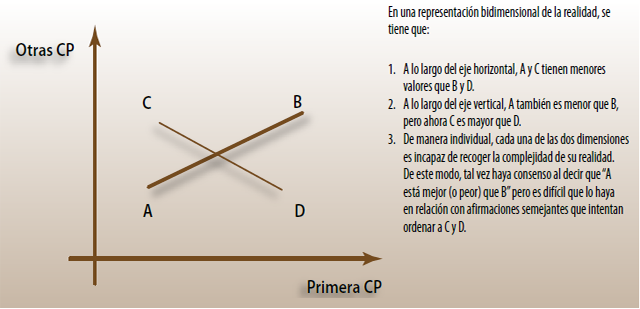
Gráfica 2

Ordenar lo que no es ordenable

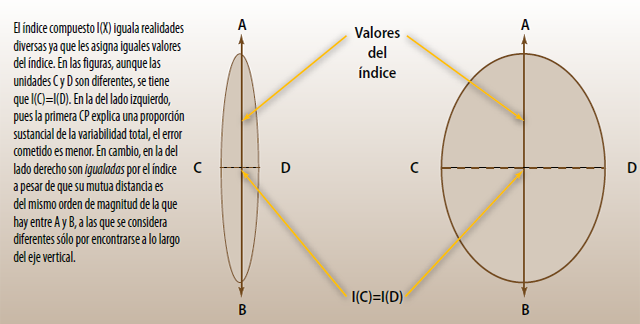
Gráfica 3

Igualar lo diferente

El tamaño de los estratos obtenidos por el CONAPO de acuerdo con su nivel de marginación se muestra en el cuadro 3. Vale la pena destacar que los municipios con alto y muy alto grado de marginación totalizan 1 251, es decir, casi 50% de los 2 454 considerados.

Cuadro 3

Tamaño de los estratos

Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7cs

Discusión crítica del procedimiento

La presente sección muestra una breve discusión de asuntos que, a nuestro juicio, deben ser tratados con mayor profundidad, pues afectan de manera significativa a los resultados obtenidos y, en consecuencia, pueden contribuir a que las políticas basadas en los mismos no abarque a la totalidad de los individuos a los que van dirigidas. Los temas que serán considerados son:

Las dos primeras hablan de una limitada eficiencia del uso que se hace de la información disponible, la tercera (consecuencia de las anteriores) debe, también, mostrar un resultado inferior al óptimo por razones obvias.

Uso de la matriz de correlaciones

A nuestro juicio, el procedimiento lleva a cabo una doble e innecesaria estandarización. Los autores del documento explican sus motivos de la siguiente manera: “Aunque el recorrido de las nueve variables está acotado por la izquierda y la derecha, es necesario transformar las variables de tal manera que aquellas con una mayor varianza no predominen en la determinación del índice y vuelvan inoperante el análisis multivariado. Con el fin de eliminar los efectos de escala entre las variables, éstas se estandarizaron mediante el promedio aritmético y la desviación estándar de cada uno de los niveles de análisis (estados y municipios)…”, según se muestra en la expresión (1).

En efecto, los índices básicos usados son expresados en porcentajes (de población, ocupantes o viviendas) por lo que las unidades originales (el efecto de escala, por ejemplo, centenares, millares o decenas de miles de personas o viviendas) ya no son un factor de preocupación en cuanto a la influencia indebida que puedan representar para el valor del índice. Es por esta razón que no resulta claro el porqué de volver a eliminar las unidades originales mediante su estandarización para llegar a las Z_ij. Si la única consecuencia de la anterior observación fuera sólo la crítica por excesiva cautela, no habría motivo de preocupación. Sin embargo, el propósito del análisis de componentes principales, que es el de señalar direcciones de máxima varianza, se pierde con esta estandarización, ya que se esferiza el problema de manera innecesaria. Pero, lo que es peor, al mismo tiempo se ocultan las inequidades, es decir, el objetivo principal del estudio.

Uso del índice con fines de conglomeración

Los métodos de conglomeración buscan conjuntar unidades lo más parecidas (homogéneas) entre sí. Los estratos homogéneos se forman a partir de los valores de una o más variables medidas en cada una de las unidades. El CONAPO usa las nueve variables de manera indirecta al conglomerar usando sólo el valor del índice de marginación, en el cual se da, en todo caso, la homogeneidad. Sin embargo, cabe preguntarse si los estratos son similares en términos de los mismos nueve indicadores básicos.

Esta situación se ilustra en la gráfica 4, la cual muestra que los cinco estratos definidos por el CONAPO incluyen municipios con 0 y 100% de pobladores en localidades con menos de 5 mil habitantes. La desviación estándar poblacional para el indicador es igual a 34.713, los valores correspondientes a cuatro estratos se encuentran entre 22 y 33, la de un quinto está cerca de 11; en otras palabras, en términos de este indicador la conglomeración no logra su cometido.

Gráfica 4

Boxplots para el porcentaje de población
en localidades con menos de 5 mil habitantes

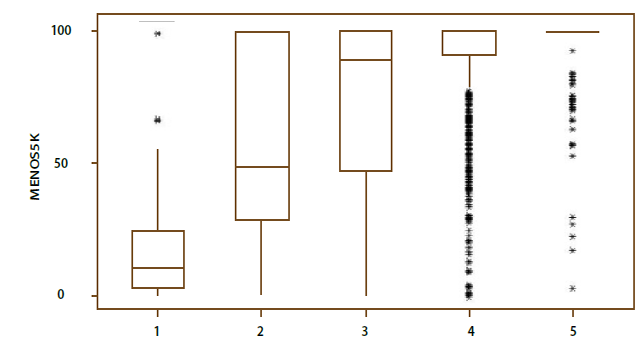
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

Consecuencias

El procedimiento según ha sido descrito es tal que:

Ya que la conglomeración es la base de numerosas políticas públicas dirigidas sobre todo a municipios y localidades con alta y muy alta marginación, existe el riesgo de que una clasificación inadecuada pueda evitar que recursos y apoyos necesarios alcancen a los sujetos de éstas.

Propuesta

A nuestro juicio, el problema multivariado de ordenamiento de unidades no tiene una solución satisfactoria, salvo cuando la primera CP explica una proporción sustancial de la variabilidad total. Por lo anterior, se sugiere atender el de conglomeración de la manera más adecuada:

El uso de las componentes principales con fines de clasificación tiene tres motivaciones principales:

Propuesta de criterio resumen para evaluar conglomeraciones

Conglomeración

Sea Ω un universo formado por N individuos o unidades, es decir, Ω ={ u₁,u₂,…u_N }. Una conglomeración multivariada S representa una partición de Ω, elaborada a partir de k mediciones realizadas en cada una de las unidades u₁,u₂,…u_N (o k indicadores básicos) de modo que el universo es descompuesto en h clases o estratos disjuntos S₁,S₂,…S_h (es decir, la conglomeración es excluyente, pues una unidad es clasificada sólo en uno de los estratos); en otras palabras, se tiene que 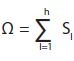En consecuencia, si N_l representa el número de unidades que componen el estrato S_l, l= 1,…,h, y N denota el tamaño de la población, debe tenerse que N = N₁+N₂+…+N_h. En este caso, se dice que la conglomeración es también exhaustiva.

Bajo las anteriores circunstancias, es claro que aún es posible determinar un gran número⁶ de conglomeraciones alternativas. Según los fines para los que se realiza la conglomeración, algunas de ellas serán más favorables que otras, pero se hace necesario estar en condiciones de medir o evaluar cuando éste sea el caso.

Medida de homogeneidad

Como ya se indicó, el propósito más importante de los métodos de conglomeración consiste en formar estratos que sean tan homogéneos de manera interna como sea posible en términos de los valores de los indicadores considerados. Una comparación entre conglomeraciones diferentes puede basarse en resúmenes de la desigualdad para cada uno de los indicadores según cada conglomeración, definidas en la expresión (3) y los que serán denominados índices de desigualdad por indicador.

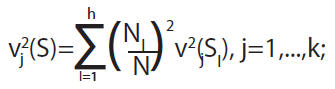(3)

donde:

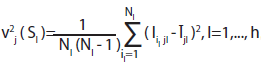
es directamente proporcional al valor de la varianza del j–ésimo indicador básico al interior de la l-ésima clase e inversamente proporcional al número de unidades que la componen, tal como ocurre con la varianza del estimador del promedio dentro del estrato.

De este modo, una clase cuyas unidades muestran gran desigualdad en los valores del indicador correspondiente y cuyo tamaño es grande, contribuirá con un valor igualmente grande al anterior criterio, alejándose del propósito de definir clases formadas por unidades homogéneas. Así, valores pequeños de la medida indicarán una mejor conglomeración en vista de su mayor homogeneidad en términos del indicador al interior de las clases. En vista de que el número de unidades en la población es fijo, es claro que serán preferibles estratos muy heterogéneos pero poco numerosos, o numerosos pero homogéneos.

Cuando los k valores definidos en la expresión (3) para una conglomeración sean todos menores que los obtenidos para otra, se dirá que la primera es más favorable que la segunda. Sin embargo, las ganancias y las pérdidas que resultan de considerar conglomeraciones alternativas (en términos de homogeneidad de las unidades al interior de los estratos) son de sentido y magnitud diversos para los indicadores básicos, por lo que se hace difícil determinar una ganadora.

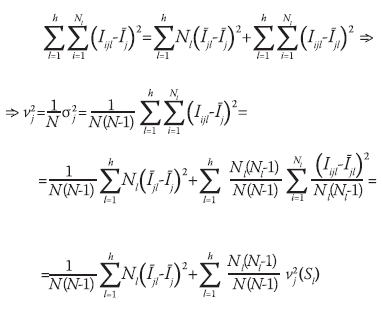(4)

donde:

I_ijl representa el valor del j-ésimo indicador para la i-ésima unidad en el l-ésimo estrato; Ī_jl , al promedio del propio indicador dentro del mismo estrato; e Ī_j , a su promedio poblacional.

Lo anterior obliga a buscar medidas que permitan evaluar de forma global los resultados alcanzados y que conduzcan a sugerir el uso de una u otra conglomeración. Jarque (1981)⁷ propuso una medida para obtener conglomeraciones multivariadas óptimas en el muestreo.

Un criterio semejante adecuado al presente contexto se obtiene a partir de la consideración de la expresión (4) hace uso de una descomposición de la suma de cuadrados de la distancia entre el valor del indicador para cada unidad y el de su promedio poblacional; en otras palabras, de un resumen de la heterogeneidad del indicador en la población. El lado izquierdo de la anterior expresión es proporcional a la varianza poblacional del i-ésimo indicador. Por su parte, el segundo término del lado derecho representa una suma ponderada, de acuerdo con el tamaño de cada estrato, de las varianzas del mismo indicador, pero esta vez dentro de cada estrato.

Cuando la conglomeración multivariada no consigue formar grupos notoriamente diferentes para alguno de los indicadores, puede tenerse que la suma de cuadrados que involucra tanto a Ī_jl como a Ī_j tome valores pequeños. Ello traería como consecuencia que algunas de las varianzas dentro de los estratos tengan órdenes de magnitud similares a los de la varianza poblacional, es decir, v²_j ≈ v²_j (S). En el otro extremo, cuando la conglomeración es exitosa para alguno de los indicadores, debe tenerse que las varianzas dentro de todos los estratos toman valores pequeños en relación con la varianza poblacional y, en consecuencia, lo mismo ocurre con la suma ponderada.

En general, se puede obtener una buena aproximación a la expresión (4), haciendo uso de la (3), como se muestra en la 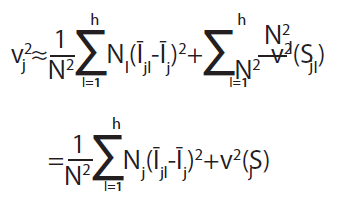(5).

(5)

Por lo anterior, con fines de comparación, se hará uso de la expresión 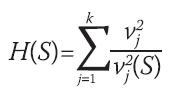(6).

(6)

Ya que el valor de v²_j representa la cota máxima para el de v²_j (S), el valor del criterio debe ser mayor para estratos homogéneos por lo que se preferirá aquella conglomeración que proporcione el valor máximo. La medida a maximizar puede, además, ser expresada en términos de lo que se denominan precisiones:

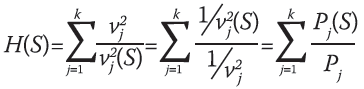(7)

En concordancia con lo antes señalado, la mínima precisión se alcanza cuando el cálculo de la varianza no considera ninguna conglomeración. La conglomeración multivariada no debe hacer peor el valor de la precisión para ninguno de los indicadores básicos. Por lo anterior, el valor de la medida será siempre mayor o igual al número de indicadores.

Según ha sido descrita, la medida propuesta no toma en cuenta la estructura de correlación exhibida por los indicadores utilizados. Sin embargo, ha sido preferida ya que, para su cálculo, la medida requiere sólo de los resultados que aporta cualquier paquete estadístico comercial.

Ejemplo numérico

Con el doble fin de comparar resultados y aclarar la contribución de cada uno de los cambios sugeridos, se seguirá una estrategia incremental:

Todas las clasificaciones obtenidas en los incisos anteriores son comparadas con base en el criterio introducido en la expresión (6). Este proceso permitirá ordenar clasificaciones alternativas y determinar la que conduce al mejor resultado.

Componentes principales a partir de la matriz de correlaciones

En esta instancia se mantienen como base de todos los cálculos los indicadores estandarizados pero, a diferencia del ejercicio llevado a cabo por el CONAPO, se obtienen conglomeraciones multivariadas partiendo de la aplicación del procedimiento de las k-medias a subconjuntos crecientes de las nueve componentes principales: en el lugar inicial, sólo la primera (1CP C); en segundo, la primera y la segunda (2CP C); en tercero, de la primera a la tercera (3CP C) y así sucesivamente hasta la que las considera a todas (9CP C). Se evalúa, también, la clasificación que usa los nueve indicadores básicos sin estandarizar ni tomar en cuenta las correlaciones existentes entre ellos (INDICES).

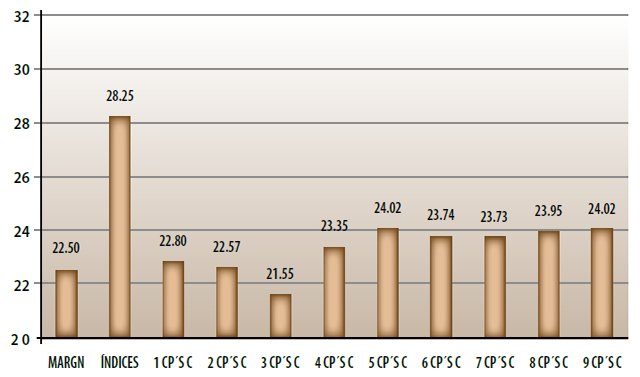
La gráfica 5 presenta los valores de H(S) correspondientes a cada una de las 11 clasificaciones anteriores. A partir de tales valores se observa, en primer lugar, que las dos clasificaciones que se basan sólo en la primera componente muestran grados de homogeneidad similares, a pesar de ser obtenidas por el procedimiento de Dalenius, en un caso y por el de las k-medias, en el otro.

Gráfica 5

Criterio resumen usando matriz de correlaciones
<
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

También, es notable y extraño el deterioro en el valor del criterio al pasar de una a tres CP, aunque se incorpora de forma gradual más información, así como su posterior mejoría al incluir CP adicionales. Se destaca, asimismo, la también cercana coincidencia de las conglomeraciones que usan cinco, ocho y nueve componentes.

De hecho, estas últimas conglomeraciones son las que resultan mejor calificadas de entre todas las que usan componentes de la matriz de correlaciones. A pesar de todo lo anterior, la mejor calificada de las mostradas en la referida gráfica es la que recurre a los nueve indicadores sin estandarizar ni tomar en cuenta su estructura de correlación. De lo anterior se concluye que, con fines de estratificación, no se hace uso eficiente de la información disponible ni incluyendo todas las componentes principales, cuando se les calcula como combinaciones lineales de las versiones estandarizadas de los indicadores y cuyos coeficientes se obtienen del análisis espectral de la matriz de correlaciones.

Componentes principales a partir de la matriz de covarianzas

Enseguida, se aplica la metodología propuesta al mismo conjunto de datos: a) calcular las componentes principales a partir de la matriz de covarianzas y b) usar un procedimiento multivariado de conglomeración (k-medias) para ser aplicado a una o más de estas componentes principales. De resultar exitosa la estrategia, se alcanzaría el fin original y principal del CONAPO de evaluar el impacto global de las carencias a la vez que, por un lado, se reduce el número original de dimensiones y, por el otro, se retiene y refleja al máximo posible la información referida a la dispersión de los datos. Sin embargo, dicho propósito no se alcanzaría a través del medio establecido, es decir, de un único índice de marginación.

El ACP a partir de los indicadores básicos no estandarizados puede ser resumido en el cuadro 4. En este caso se observa que la primera componente principal aporta una explicación ligeramente mayor a la obtenida usando los indicadores estandarizados y que la suma de las dos primeras representa más de tres cuartas partes del mencionado total. Gracias a lo anterior, basta con cuatro componentes para rebasar 90% del total y la aportación de las cuatro últimas es menos significativa que las correspondientes calculadas a partir de la matriz de correlaciones.

Cuadro 4

Valores propios de la matriz de covarianzas

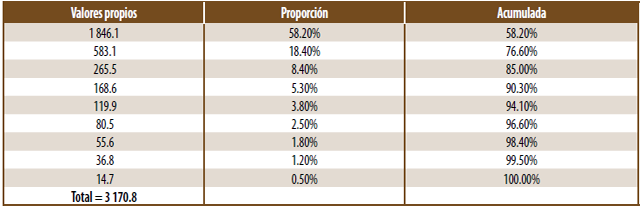
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

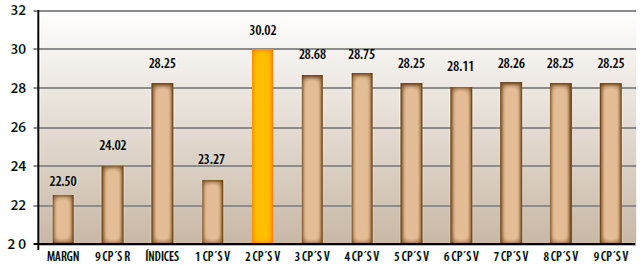
Con base en los valores que toma cada una de las componentes principales en los elementos de la población de municipios, se obtuvieron nueve clasificaciones adicionales para los municipios mexicanos. La gráfica 6 muestra los valores de H(S) para 12 conglomeraciones diferentes: por un lado las ya comentadas MARGN, INDICES y las 9CP C, y por el otro las nueve que resultan al usar conjuntos crecientes de componentes principales, las que serán denotadas por 1CP V, 2CP V, …, 9CP V, en notación similar a la usada antes.

Gráfica 6

Criterio resumen

Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en bit.ly/3zT7j7c

La información resumida en la gráfica deja claro que las conglomeraciones basadas en el uso de una sola componente principal, sea ésta calculada a partir de la matriz de correlaciones o de la de covarianzas, resultan ser las peor clasificadas de acuerdo con el criterio utilizado. Más aún, aunque los resultados parecen mejorar de forma ligera, el uso de todas las componentes principales de la matriz de correlaciones también muestra un comportamiento deficiente.

Por otro lado, llama la atención que la implementación de Minitab para el algoritmo de las k-medias conduce a la misma conglomeración tanto cuando se usan los nueve indicadores básicos como cuando se emplean las nueve componentes principales. Lo anterior podría llevar a la conclusión de que no es necesario hacer nada más pues, al hacer uso de las componentes principales, se ha tomado en cuenta una de las más importantes objeciones a este procedimiento, es decir, el hecho de que no aprovecha la información sobre las correlaciones entre los indicadores. De hecho, podría encontrarse sustento adicional para alcanzar tal conclusión sobre la base de que se ha hecho uso de toda la información disponible pues hasta la intrascendente última componente principal habría sido tomada en cuenta.

Sin embargo, la evaluación a través del criterio propuesto de todas las conglomeraciones elaboradas lleva de inmediato a concluir que el mejor valor de dicho criterio se alcanza con la conglomeración basada en el uso de sólo las dos primeras componentes principales. Los resultados parecen indicar que la información restante contenida en cualesquiera indicadores adicionales no correlacionados con las dos primeras componentes principales, las dos influencias más importantes, tiene más bien un comportamiento ruidoso o aleatorio, por lo que no contribuyen a mejorar posteriores clasificaciones de municipios.

Por su parte, además de los tamaños en los estratos, la gráfica 7 muestra la que es, sin duda, la ganancia más importante en términos de los indicadores básicos al pasar de MARGN a la estratificación óptima: el indicador de ruralidad tiene un comportamiento más homogéneo al interior de los nuevos estratos. Como se observa, la conglomeración MARGN da lugar a estratos, todos los cuales contienen unidades con valores muy pequeños o muy grandes para este indicador.

Gráfica 7

Boxplots para MENOS5K según las conglomeraciones marginación vs. óptima


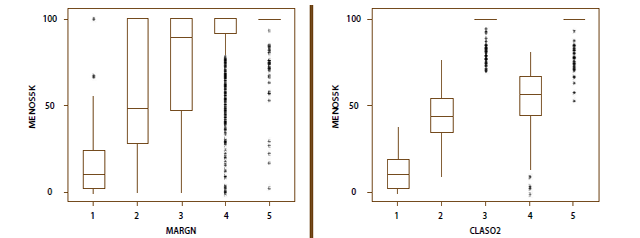
Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009 en www.conapo.gob.mx/publicaciones/margina2005/AnexoB.xls

A partir de este resultado es también posible ver que los nuevos estratos con grado de marginación medio (3) y muy alto (5) están formados casi en su totalidad por municipios rurales, en tanto que el que se identificaría con alto grado de marginación (4) tiene una composición más bien mixta. Ello conduce a evitar la conclusión, tal vez errónea, que se extraería de la conglomeración MARGN, en el sentido de que un grado alto o muy alto de marginación parece estar ligado a una mayor ruralidad.

El cuadro 5 permite, a su vez, comparar el resultado de conglomerar municipios a partir de, por un lado, los valores del índice de marginación y, por el otro, los de las primeras dos componentes principales calculadas usando la matriz de covarianzas, cruzando la forma en que cada municipio es clasificado en cada caso. Se destaca en particular el importante desplazamiento de municipios entre clases alternativas. Por su número, sin duda, el efecto más importante de pasar de una clasificación a la otra es la salida de 470 municipios de las clases con alto y muy alto grado de marginación. En sentido contrario, sólo 37 municipios que tenían una clasificación diversa ingresan en alguna de estas dos clases.

Cuadro 5

Conglomeraciones: marginación vs. óptima

Cálculos propios mediante Minitab usando archivo de datos encontrado el 20 de noviembre de 2009, en bit.ly/3zT7j7c

El efecto de lo anterior en términos poblacionales puede ser visto usando la información del Conteo 2005. En los 470 municipios que abandonan las categorías de muy alto y alto grado de marginación en el 2005 habitaban 4 339 251 personas. Por su parte, en los 37 que son ahora clasificados dentro de la categoría de alto grado de marginación residían, en aquel año, 1 287 197.

Conclusión

Se presentó una estrategia a seguir para lograr la conglomeración de unidades de una población. Partiendo de las componentes principales basadas en la matriz de covarianzas, se clasifican las unidades de la población con base en los valores de las componentes. Se procede de manera incremental obteniendo la primera clasificación que considera sólo a la primera componente; la segunda clasificación que considera tanto a la primera como la segunda componentes; la tercera, a las primeras tres y así sucesivamente hasta llegar a la que considera a todas las componentes principales. Las clasificaciones alternativas son comparadas con base en el criterio introducido en este trabajo y cuyo valor máximo determina la clasificación formada por estratos más homogéneos en su forma interna.

De esta manera, se alcanza el fin original y principal del CONAPO de evaluar “…el impacto global de las carencias…” a través de un medio que, para “…facilitar el análisis de la expresión territorial de la marginación, reduzca la dimensionalidad original y, al mismo tiempo, se retenga y refleje al máximo posible la información referida a la dispersión de los datos (…) así como las relaciones entre ellos…”; sin embargo, dicho propósito no se alcanza a través del medio establecido por esta institución, es decir, de un único índice de marginación. De cualquier modo, bajo condiciones excepcionales que se dan cuando la primera componente principal explica una proporción sustancial de la suma de las varianzas de los indicadores originales, no se impide que ésta sea una posibilidad, en cuyo caso se podrá además “…establecer una ordenación entre las unidades de observación: estados, municipios o localidades.”

Es preciso reiterar que el propósito de este artículo no es el de sugerir el uso de un conjunto u otro de indicadores cuando se realiza un ejercicio de clasificación. Es por ello que el significado de la variable que tiene mayor influencia en la conglomeración óptima alcanzada no es relevante para la discusión que se presenta. Sin embargo, ya que para el caso de ejemplo éste no es sino un sucedáneo para medir las condiciones de ruralidad de un municipio, se sugiere evitar el trabajar con variables resumen para una o más de las dimensiones que se estudian e incluir de manera explícita tantas variables como se considere necesario para lograr una buena conglomeración.

Ésta es la estrategia seguida por el ejercicio denominado niveles de bienestar, desarrollado por el INEGI con base en la información de los censos de 1990 y del 2000. Por supuesto, tampoco se aboga por la aplicación de tal ejercicio en las mismas condiciones en que fue realizado ya que, como se ha visto, puede conducir a una solución subóptima. En efecto, por así decirlo, permite que el ruido y la redundancia en los indicadores afecten el resultado. Una vez que se considera el uso de dos o más componentes principales como insumo al procedimiento multivariado de conglomeración y que se dispone de un criterio adecuado que permite identificar el resultado más adecuado, la dimensión del problema alcanzará un tamaño razonable y conducirá a conglomeraciones adecuadas.

¹ Nardo, M.; Saisana, M.; Saltelli, A.; Tarantola, S.; Hoffman, A.; Giovannini, E. (2005). Handbook on Constructing Composite Indicators: Methodology and User Guide. OECD Statistics Working Paper, recuperado en: bit.ly/4deBsMB bit.ly/4deBsMB

² bit.ly/3SpUIPj

³ CONAPO. (2006). Índices de marginación, 2005. México, DF, recuperado en bit.ly/3YiONPJ

⁴ Procedimiento de Dalenius, óptimo en el sentido de mínimo coeficiente de variación en la estimación conglomerada del promedio de un indicador; en este caso, la primera componente principal.

⁵ bit.ly/3YiONPJ

⁶ h^N cuando se permite que N_l =0, para uno o más valores de l.

⁷ Jarque, C. M. (1981). A Solution to the Problem of Optimum Stratification in Multivariate Sampling. Series C (Applied Statistics). JRSS, 30 (2), 163-169, en bit.ly/4bYb60u.