Ajuste estadístico a la distribución del ingreso en el Módulo de Condiciones Socioeconómicas 2015 mediante imputaciones múltiples
Statistical Adjustment to Income Distribution in the MCS 2015 through Multiple Imputations
Delfino Vargas Chanes* y Servando Valdés Cruz**
*Programa Universitario de Estudios del Desarrollo (PUED) de la Universidad Nacional Autónoma de México (UNAM), dvchanes@unam.mx y dvchanes@gmail.com
** PUED de la UNAM, servando.valdes.cruz@gmail.com
Vol. 9 número especial – Epub Ajuste estadístico… – Epub

|
El presente artículo se relaciona con el tema del ajuste estadístico al ingreso capturado en el Módulo de Condiciones Socioeconómicas (MCS) 2015 con fines de comparabilidad con la serie histórica del ingreso. Esta aproximación parte del supuesto de que la distribución del ingreso para el MCS 2015 está sobreestimada para los deciles I a VI y que los superiores no tienen ese problema; también, se supone que las carencias sociales están bien capturadas. La propuesta consiste en utilizar el método de imputaciones múltiples bajo el supuesto Missing at Random (MAR) eliminando los deciles I a VI de la distribución del ingreso de los hogares del 2015. Las bases de datos MCS 2014 y 2015 se unen de forma vertical, con 35 covariables homologadas relacionadas con los ingresos bajos. Primero, se evalúa el modelo de imputación a través de un modelo logístico para validar el supuesto MAR. El segundo paso consiste en realizar imputaciones múltiples para el ingreso faltante y se simulan 10 bases de datos usando técnicas de Monte Carlo que completan el ingreso omitido (los deciles I a VI solo para el 2015) creando 10 versiones completas de datos. El tercer paso consiste en estimar 10 modelos de regresión que se resumen en uno solo (al final del proceso) que incluyen las 35 variables relacionadas con pobreza como predictores del modelo de imputación. Al final, con este modelo se imputan las observaciones faltantes de la cola inferior del ingreso para el 2015. A partir de la base de datos imputada se aplica la metodología del CONEVAL para estimar la pobreza. Los resultados indican que la pobreza a nivel nacional es de 42.4%, que representan a 51.4 millones de personas, una pobreza extrema de 8.4% en 10.2 millones de personas y un coeficiente de Gini de 0.492. Palabras clave: imputación múltiple; pobreza; desigualdad; ajuste distribución-ingreso. |
This article addresses the adjustment of income distribution captured by the Module of Social Conditions of 2015 (MCS 2015) for the purpose of comparability with the historical series of income. This approach is based on the assumption that the income distribution for MCS 2015 is over estimated for deciles I to VI and that the upper deciles do not have that problem. It is also assumed that social lag variables are well captured. The purpose of this article consists of using Multiple Imputations method under MAR (Missing at Random) assumption, eliminating the deciles I to VI of the household income distribution of 2015. The MCS 2014 and 2015 databases are vertically merged, with 35 covariables related to low income. First, the imputation model is evaluated through a logistic model to validate the MAR assumption. The second step is to perform multiple imputations for the missing income and simulate 10 databases using Monte Carlo techniques that complete omitted income (deciles I to VI only for 2015) by creating 10 complete versions of data. The third step consists of estimating 10 regression models that are summarized in a single model (at the end of the process) that includes the variables related to poverty, as predictors of the imputation model. Finally, with this model, the missing observations of the lower income distribution tail for the year 2015 are imputed. From the imputed database, the CONEVAL methodology is applied to estimate poverty. The results indicate that poverty at the national level is 42.4%, representing 51.4 million people, extreme poverty of 8.4% representing 10.2 million people and a Gini coefficient of 0.492.
Key words: multiple imputation; poverty; inequality; income-distribution adjustment. |
Introducción
La estimación de la pobreza y la desigualdad han sido un tema de interés nacional por sus implicaciones en la política pública, ya que son elementos sustanciales para la asignación de presupuesto a los programas y acciones federales de desarrollo social. El uso de las encuestas que miden el gasto y el ingreso de los hogares hace posible, para otras instituciones, focalizar los programas sociales para incrementar la eficiencia de las acciones gubernamentales dirigidas a combatir la pobreza y el desarrollo social.
El Instituto Nacional de Estadística y Geografía (INEGI) es el encargado de realizar los operativos tanto del Módulo de Condiciones Socioeconómicas (MCS) y de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH), mientras que el Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) tiene como una de sus tareas procesar los resultados de esos operativos para medir la pobreza multidimensional.
El enfoque que se propone en el presente artículo utiliza un método estadístico llamado imputaciones múltiples, que permite la comparabilidad del ingreso del 2015 con años anteriores (2010 al 2014);1 sin embargo, parte de supuestos (como todo modelo estadístico). El primero es que la tendencia general de las carencias sociales mantiene su comportamiento tendencial, es decir, que las carencias sociales observadas en el 2010, 2012, 2014 y 2015 han sido medidas de forma correcta y constituyen uno de los soportes fundamentales para estimar el ingreso del 2015. El segundo es que no todos los deciles de ingreso tienen que ser estimados, ya que los cambios observados en el MCS 2015 solo afectaron en los deciles inferiores de ingreso y, en menor medida, a los ingresos de los deciles superiores. De esta manera, el ingreso imputado para el MCS 2015 permite la comparabilidad del ingreso con la serie histórica del 2010 al 2015 y, en consecuencia, con la pobreza multidimensional.
El artículo incluye seis secciones. En la primera se muestra la tendencia general de la pobreza y justifica de alguna manera la necesidad de hacer comparables los resultados sobre el tema con las encuestas anteriores. En la segunda se justifican parte de los supuestos de la imputación al llamar la atención sobre la serie histórica de las carencias y su relación con la pobreza. En la tercera se explica el procedimiento de imputación múltiple. En la cuarta se presentan otros enfoques usados para calibrar el modelo. La quinta se dedica a presentar los resultados de la imputación múltiple. En la última se dan las conclusiones.
Tendencia de la pobreza multidimensional y las carencias sociales
El CONEVAL utiliza el soporte normativo que le da la Ley General de Desarrollo Social (LGDS), la cual utiliza dos enfoques: el de bienestar —que incluye los ingresos— y el de los derechos humanos —que incorpora las carencias sociales— (CONEVAL, 2011). La figura 1 muestra la evolución de la pobreza en las mediciones bianuales de pobreza multidimensional del 2010 al 2015. En esta figura, los datos del 2015 no fueron calibrados y rompen la serie histórica que no permiten la comparabilidad con años anteriores.
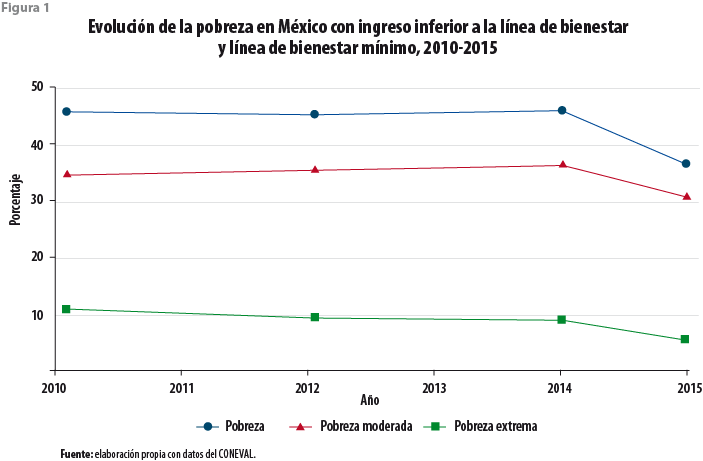
Por otro lado, la figura 2 muestra las seis carencias sociales del 2010 al 2015 (e. g., rezago educativo; acceso a servicios de salud, a los servicios básicos de la vivienda y a la alimentación; seguridad social; así como calidad y espacios en la vivienda). En general, se observa en esta figura una reducción de éstas, con excepción de las que se refieren a la alimentación y a los servicios básicos de la vivienda. Observamos consistencia en la medición de ellas, que dan muestra de una medición consistente en el tiempo observado y constituye uno de los supuestos del modelo de imputación.
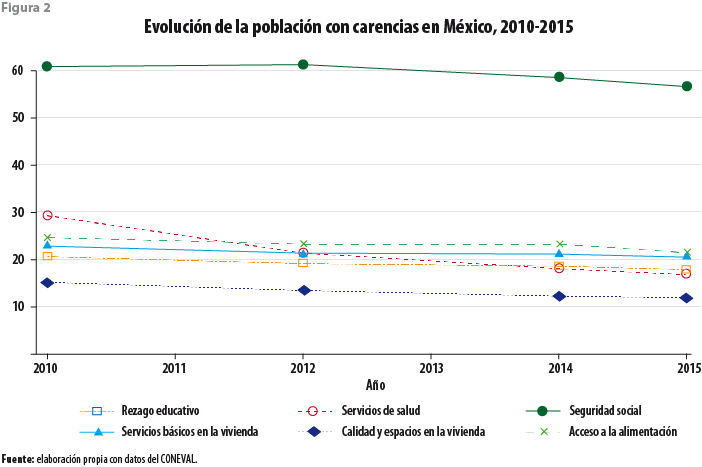
Deciles de ingreso
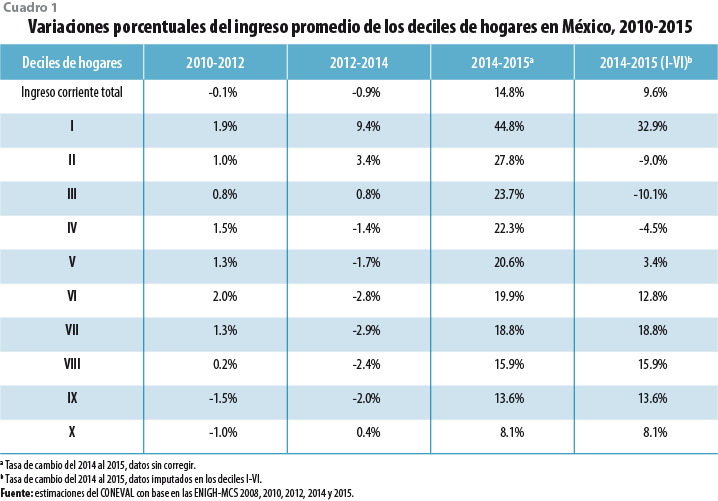
Otro de los supuestos usados para el presente ejercicio es que los deciles inferiores se vieron más afectados que los superiores. El cuadro 1 muestra la variación porcentual del ingreso promedio de los deciles de hogares. Por ejemplo, la tasa anual del 2010-2012 es -0.1%, muy similar a la del 2012- 2014 que es de -0.9%; sin embargo, la tasa anual del 2014-2015 muestra un incremento de 14.8%; cuando se imputan los datos, la tasa anual es de 9.6 por ciento. Un razonamiento similar se puede hacer para cada decil, de manera que los deciles más afectados son del I al VI, donde se observan los mayores incrementos.
Procedimiento de imputación
Para reconstruir la comparabilidad de la serie histórica del ingreso, los datos se organizan de manera transversal usando los MCS 2014 y 2015; la base de datos (BD) contiene las variables x1 a x352 usadas para el modelo de imputación (ver el Anexo 1). La variable de interés para realizar las correcciones es el ingreso del hogar deflactado al 2015.3 Las BD se codifican de manera homogénea para que las variables tengan el mismo sentido en los dos años; también, algunas de éstas contienen datos faltantes, pero el énfasis es imputar el ingreso de los hogares del 2015.
La habilidad para imputar datos faltantes depende del conocimiento que se tenga acerca del mecanismo que los produce. En la literatura se reconocen tres mecanismos: completamente al azar (MCAR, por sus siglas en inglés), al azar (MAR, por sus siglas en inglés) y no ignorable (NI); para más información, ver Rubin (1987). El primero supone que éstos no se relacionan con ninguna covariable que explique la razón de su ausencia; es muy raro en la práctica y se puede inducir cuando el investigador asigna al azar los ítems faltantes; la imputación de datos bajo este esquema es muy sencilla. El segundo implica que existen covariables identificadas que explican la ausencia de los datos en la muestra; para ello, se requiere identificar un modelo de imputación que contiene variables que explican este mecanismo (Schafer y Olsen, 1998). El tercero supone que los datos faltantes se explican por un mecanismo endógeno, es decir, no hay covariables que expliquen la ausencia, que el incremento/decremento de la variable de interés incrementa/decrementa la probabilidad de estar ausente de la base de datos; este mecanismo es el más difícil de tratar de forma estadística. Por fortuna, los mecanismos MCAR y NI ocurren con menor frecuencia y el MAR, aparece en 90% de los casos (Enders, 2010).
Formalmente hablando, supongamos que una matriz de datos incluye los valores observados y los faltantes, y se denota por Y = (Yobs ,Yfalt) , donde Yobs se refiere a los observados y Yfalt es la matriz de los faltantes. La función de densidad de probabilidad se denota por:
![]() (1)
(1)
donde θ indica los parámetros que determinan la distribución de Y. Para entender mejor los mecanismos de datos faltantes, suponga que R es una matriz de indicadores con las mismas dimensiones de la matriz de datos original, donde cada elemento de R contiene 0 si el elemento es faltante y 1 si está presente. La función de densidad condicional se denota por:
![]() (2)
(2)
donde ɸ es la distribución condicional de R dado el conjunto de datos completos Y. En esta expresión, los datos completos observados se reemplazan e integran sobre la porción faltante y se expresan de la siguiente manera:
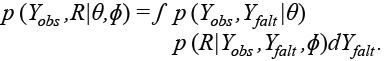 (3)
(3)
El mecanismo MCAR no depende de los valores observados ni de los faltantes, entonces se define como:
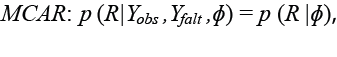 (4)
(4)
Este mecanismo es equivalente a borrar al azar un conjunto de datos a partir de una matriz Y completa, donde cada observación tiene igual probabilidad de ser borrada.
El segundo mecanismo, el MAR, formalmente quiere decir que la distribución de los valores faltantes depende solo de los valores observados. Entonces:
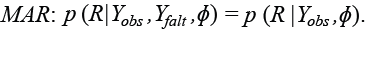 (5)
(5)
En otras palabras, el mecanismo de los valores faltantes se puede encontrar en los valores observados.
Por último, el mecanismo NI se puede encontrar en los valores faltantes y no en los observados, por lo tanto:
 (6)
(6)
Los modelos de imputación y el analítico
Cuando se realizan imputaciones es importante distinguir entre ambos modelos. El de imputación es el que tiene covariables que explican la probabilidad de que un dato sea faltante; de esta manera, resulta muy útil conocer todas las covariables que explican el proceso de imputación. En tanto, el modelo analítico es el que consiste en analizar los valores imputados. De manera típica, bajo el modelo MCAR, los de imputación y el analítico son los mismos o casi iguales. Bajo el supuesto MAR, la calidad de la imputación está asociada con selección de las variables del modelo de imputación (Graham y Schafer, 1999; Russell, Stern y Sinharay, 2000); por ejemplo, Graham y Schafer muestran que los estimadores de los parámetros tienen menor sesgo en relación con los parámetros poblacionales cuando se incrementa el número de covariables en el modelo de imputación. Por lo tanto, la estrategia que usamos en el documento consiste en incorporar un número considerable de covariables para mejorar la calidad de las imputaciones que estén relacionadas con el ingreso. En nuestro caso, utilizamos de preferencia covariables relacionadas con la población con ingresos bajos, pues partimos del supuesto de que los valores faltantes son los de la cola inferior del ingreso. El modelo de imputación es logístico, donde el valor de 1 se asigna para los valores faltantes y 0 cuando son observados (ver el Anexo 1, donde se muestran las covariables).
Imputación múltiple (IM)
Incorpora un proceso de simulación para completar los valores faltantes dado que un solo valor no refleja la variabilidad, la cual es el resultado del proceso de simulación de datos que resultan de un proceso de Monte Carlo; de esta manera, se obtienen varias versiones completas de datos y, después, se ajusta un modelo analítico para cada conjunto. El modelo analítico es el resumen de todos los modelos ajustados en uno solo, para el cual se aplican las reglas de Rubin (1987:76-77).
Uno de los métodos de Monte Carlo usado en IM consiste en aumentar los datos faltantes, que contiene el paso-I y el –P. El -I obtiene una muestra aleatoria de las observaciones a partir de la distribución marginal en la primera iteración:

El paso–P obtiene una muestra aleatoria de parámetros de la distribución marginal que incorpora los valores observados e iniciales de los valores faltantes del -I en la primera iteración:

El paso-I y el –P de la primera iteración proporcionan los valores iniciales ![]() , así como las iteraciones posteriores para crear una Cadena de Markov con valores
, así como las iteraciones posteriores para crear una Cadena de Markov con valores ![]() que convergen en distribución a p(θ,Yfalt |Yobs ) , con la finalidad de crear una cadena de observaciones completa
que convergen en distribución a p(θ,Yfalt |Yobs ) , con la finalidad de crear una cadena de observaciones completa ![]() , lo cual es equivalente a correr m cadenas independientes o iteraciones de calentamiento, de tamaño t.
, lo cual es equivalente a correr m cadenas independientes o iteraciones de calentamiento, de tamaño t.
Un aspecto importante a considerar es probar la convergencia del proceso de cadenas múltiples de Monte Carlo (MCMC), así como el número de iteraciones que se requieren para que el proceso converja; estos aspectos dependen de la cantidad de datos faltantes. Sin embargo, el algoritmo requiere de un mínimo de iteraciones de calentamiento m para garantizar que una cadena θ(t+m) sea independiente de θ(t). Una vez que se cumpla esta condición, cada valor del parámetro estimado θ puede tomarse como una extracción independiente de p(θ|Yobs) y, en consecuencia, Yfalt se puede usar como valor imputado.
Se han propuesto varios métodos para investigar la convergencia de la distribución conjunta para un valor específico de m (Ritter y Tanner, 1992; Roberts, 1992). Desde un punto de vista práctico, la función de autocorrelación (ACF) se puede usar para determinar la convergencia del algoritmo para cada rezago-p de la serie estacional {k(t) :t =1,2,…,k} ; la ACF se define como:

La gráfica de ACF vs. p para un valor p finito muestra un correlograma que ayuda a identificar la dependencia lineal potencial de las iteraciones. Si muestra un decaimiento súbito para los valores de p = 2 a 4, sugieren una independencia serial, lo cual quiere decir que el algoritmo converge a una solución satisfactoria (Box y Jenkins, 1976). Existen otros métodos para asegurar la convergencia que usan un enfoque Bayesiano que también se pueden considerar como criterios de convergencia, que no se usan en el presente trabajo (Casella y Berger, 2001; Gilks, Richardson y Spiegelhalter, 1996).
Otros métodos de imputación
Con la finalidad de calibrar el modelo de regresión obtenido a partir de la imputación múltiple se probaron dos enfoques más. El primero fue el de la imputación vía regresión, el cual completa los datos faltantes usando un enfoque Gaussiano (Gelman, Carlin, Stern y Rubin, 2004; Rubin, 1987; Shenker y Taylor, 1996). Este método parte de la idea de que los datos están completos en las covariables4 excepto en la variable de respuesta, que en nuestro caso es el ingreso. Para este ejercicio, también se omitieron los ingresos de los deciles I a VI del MCS 2015 del ingreso que se busca imputar.
La figura 3 muestra la distribución de valores observados y se encuentra en la parte H y los valores faltantes, en la L. El modelo de regresión estimado contiene las 35 variables previamente definidas (ver variables en el Anexo 1). El modelo estimado resulta ser muy similar (con diferencias en las milésimas) al ajustado vía regresión por imputación múltiple. Al estimar la incidencia de la pobreza usando la metodología del CONEVAL se obtienen prácticamente los mismos resultados.

El segundo enfoque fue el de imputación vía máxima verosimilitud con información completa (FIML, por sus siglas en inglés). Se probó ajustar otro método de estimación del modelo de regresión, bajo el supuesto MAR, usando el método de FIML (Arbuckle, 1996; Muthén, Kaplan y Hollis, 1987), el cual se basa en el trabajo de Little & Rubin (1987) y utiliza el supuesto de que el mecanismo de ignorabilidad es MAR; es decir, que los valores faltantes se pueden recuperar a partir de los datos observables. En realidad, el método FIML no produce imputaciones, sino que utiliza la información disponible para obtener estimaciones de máxima verosimilitud para el modelo de regresión propuesto. Este enfoque genera una función de máxima verosimilitud basada en una matriz de covarianzas de todos los posibles subconjuntos de variables donde la información es completa. Mediante FIML se pueden usar diferentes patrones de datos incompletos. La BD es la misma que en los otros métodos (ver figura 4), donde igualmente se elimina el logaritmo del ingreso de los deciles I a VI. Se ajusta el modelo ![]() , donde
, donde ![]() es el valor estimado y
es el valor estimado y ![]() es el vector de parámetros estimados, y se procede a estimar los valores faltantes de los deciles I a VI. Como último paso, se calcula la pobreza usando la metodología del CONEVAL. Los resultados son los mismos que con los otros métodos, por lo tanto, enseguida se reportan los resultados obtenidos vía imputaciones múltiples.
es el vector de parámetros estimados, y se procede a estimar los valores faltantes de los deciles I a VI. Como último paso, se calcula la pobreza usando la metodología del CONEVAL. Los resultados son los mismos que con los otros métodos, por lo tanto, enseguida se reportan los resultados obtenidos vía imputaciones múltiples.

Resultados
El procedimiento
La base de datos que usaremos es de los MCS 2015 y 2014, como lo hemos establecido en párrafos anteriores; el modelo de imputación utiliza las variables que se indican en el Anexo 1, las cuales se relacionan con la pobreza, ya que el modelo busca predecir el ingreso de los deciles con menores ingresos.
El primer paso consiste en ajustar un modelo de imputación para justificar el supuesto de MAR (Rubin, 1987; Schafer, 1997); para ello, se ajusta un modelo logístico.5 La variable de respuesta es Y* = 1 si el valor es faltante y Y* = 0 si está presente; se usaron las 35 covariables presentes en la BD, donde Y * es el logit:
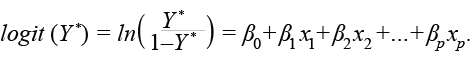
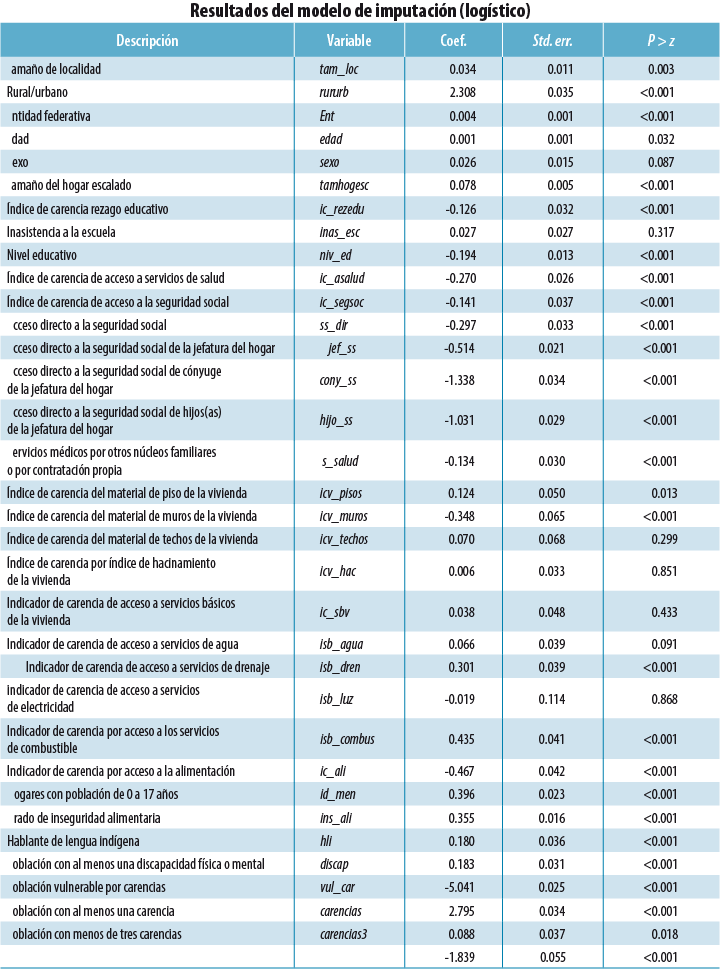
El modelo de imputación muestra un buen ajuste, ya que tiene 87.3% de casos correctamente clasificados con una sensibilidad de 81% y especificidad de 90.9 por ciento. Los coeficientes de las covariables fueron todos significativos, con excepción de cinco (ver el Anexo 2).
El modelo analítico es un modelo de regresión y tiene la siguiente forma:
![]()
donde Y = ln (ingreso del hogar+k) es el logaritmo del ingreso corriente total mensual del hogar. Las variables predictoras se muestran en el Anexo 1. Se busca la mejor transformación del ingreso mediante el log ( y + k ) y encontramos que el valor de la constante que minimiza el sesgo y corrige la curtosis es k = 503.57. Con dicha transformación se disminuye la asimetría y la curtosis, aun cuando el estadístico D de Lilliefors rechaza la normalidad ( p<0.001); no obstante, la asimetría y la curtosis son casi nulas (ver cuadro 2).
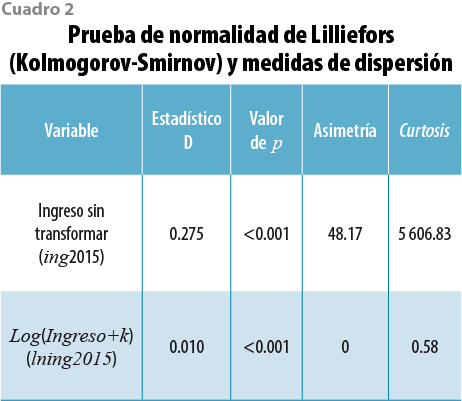
La base de datos cuenta con 35 variables homologadas para el 2014 y 2015; usando el ingreso por hogar se ajustan tres escenarios: en el primero se eliminan los ingresos de los deciles I al IV; en el segundo, los del I al V; y el tercero, los del I al VI para el MCS 2015. Ya que suponemos que el ingreso del hogar está sobreestimado en estos deciles, al ajustarlos nos permitirá que la serie sea comparable con las BD anteriores (ver figura 4).
En segundo lugar se aplica el método de imputaciones múltiples (Rubin, 1987; Schafer y Graham, 2002; Vargas Chanes y Lorenz, 2015) que usa métodos de Monte Carlo, donde se simulan 10 conjuntos completos que contienen los datos imputados.6 La garantía de que hay convergencia en las simulaciones y en la parte de imputación de los datos se juzga a partir de la peor función lineal (WLF, por sus siglas en inglés) y de la función de autocorrelación (ACF) de la WLF; por ejemplo, si la WLF (figura 5a) muestra ruido blanco y la ACF (figura 5b) presenta una caída de las autocorrelaciones para p > 4, entonces hay cierta garantía de que el proceso converge de manera satisfactoria.7
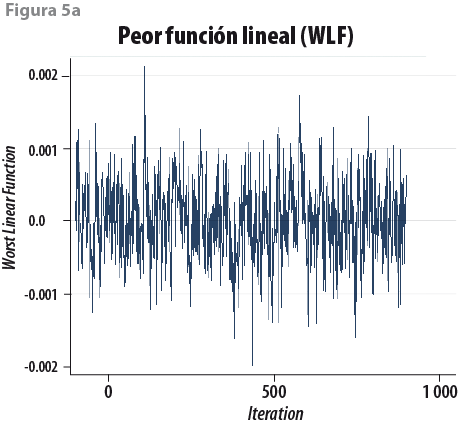
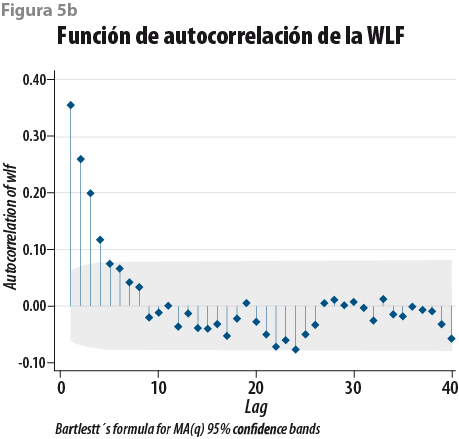
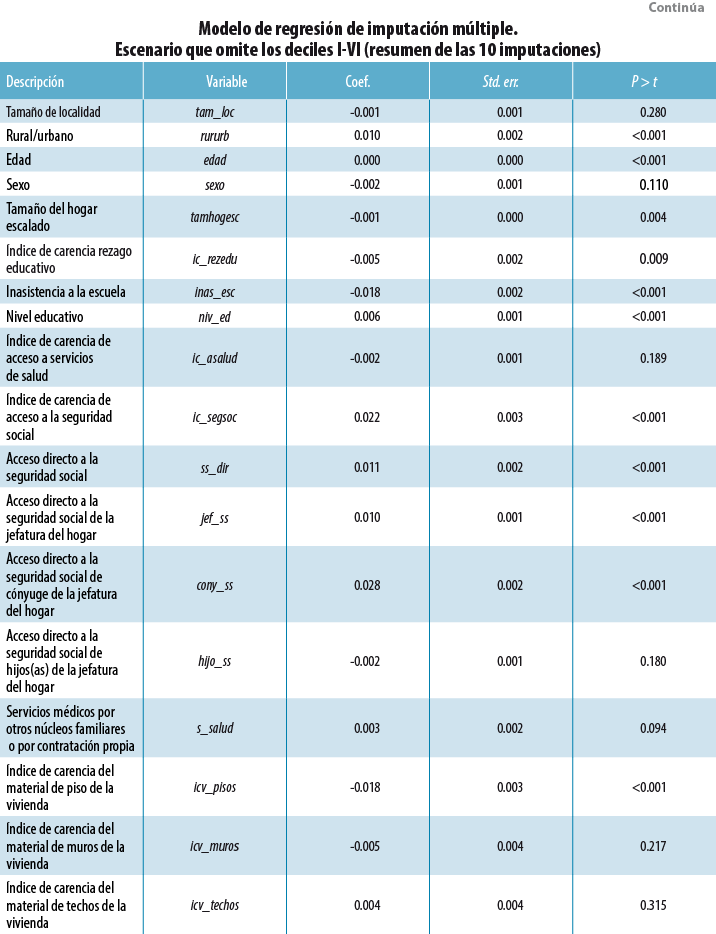
El siguiente paso consiste en ajustar un modelo de regresión para los 10 conjuntos de datos completos y se consolida en un modelo final usando las reglas de Rubin (1987:76-77). Este modelo usa las 35 variables previamente mencionadas (ver Anexo 38 ) y permite estimar los valores del ingreso faltante para los tres escenarios plantados (e. g, omitiendo los deciles I-IV, I-V y I-VI del MCS 2015).
En suma, el ingreso se estima a través del modelo ajustado vía imputaciones múltiples ![]() , donde
, donde ![]() es el valor estimado y
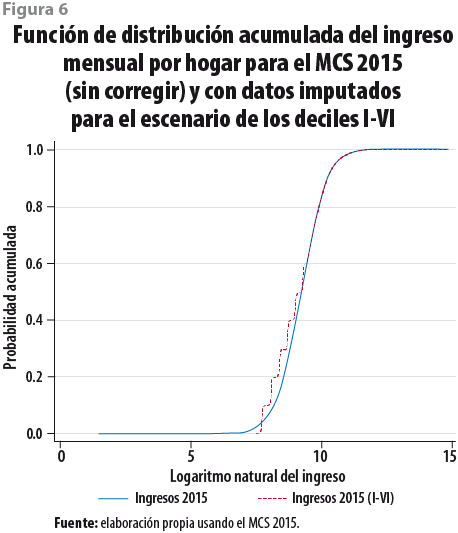
es el valor estimado y ![]() el vector de parámetros resumidos mediante las reglas de Rubin para los tres escenarios al imputar los deciles I-IV, I-V y I-VI. Se obtiene el anti-log de los ingresos estimados y se procede a calcular la pobreza empleando la metodología del CONEVAL; los ingresos mensuales de los hogares se calculan per cápita, con lo que se tienen los resultados que a continuación se muestran en el siguiente subapartado de esta sección. La figura 6 presenta la función de distribución acumuada (FDA) del ingreso mensual por hogar para el MCS 2015 en sus dos versiones, la FDA sin corregir en línea continua y los deciles I al VI imputados en línea punteada.
el vector de parámetros resumidos mediante las reglas de Rubin para los tres escenarios al imputar los deciles I-IV, I-V y I-VI. Se obtiene el anti-log de los ingresos estimados y se procede a calcular la pobreza empleando la metodología del CONEVAL; los ingresos mensuales de los hogares se calculan per cápita, con lo que se tienen los resultados que a continuación se muestran en el siguiente subapartado de esta sección. La figura 6 presenta la función de distribución acumuada (FDA) del ingreso mensual por hogar para el MCS 2015 en sus dos versiones, la FDA sin corregir en línea continua y los deciles I al VI imputados en línea punteada.
Ingreso corriente y pobreza multidimensional
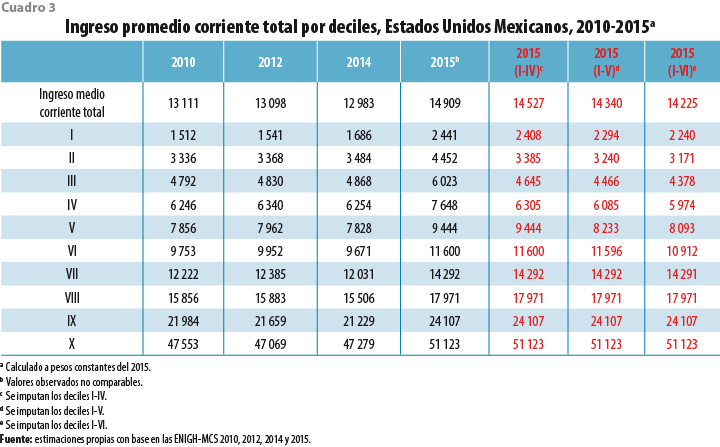
Los ingresos medios por deciles para los años 2010 al 2015 (originales e imputados) a precios constantes del 2015 se muestran en el cuadro 3. Se observa que en la última columna de ingresos medios totales por hogar (imputados para el 2015, deciles I-VI) tienen un incremento de 9.6% en relación con el 2014 y el primer decil tiene 32.9% de incremento en el ingreso. Los deciles II al IV muestran pérdidas de ingreso de 4 a 10%; el resto de los deciles superiores presentan incrementos en el ingreso de 8 a 18 por ciento.
Los resultados de la pobreza multidimensional del 2010 al 2015 se muestran en el cuadro 4; se presentan dos versiones del MCS 2015: la reportada por el INEGI en su primera versión y la corregida por el método de imputación múltiple usando tres escenarios (deciles I-IV, I-V y I-VI), los cuales dan muestra del grado de sensibilidad de los deciles imputados. Mientras más deciles se incorporen al modelo de imputación, la pobreza se incrementa, de 40.2% para el escenario I-IV hasta 42.4% para el del I-VI. También, la desigualdad se incrementa de 0.478 para el escenario I-IV hasta 0.492 para el del I-VI. Nos preguntamos, ¿cuál de los tres escenarios presenta una mejor corrección? La respuesta está en el supuesto del número de deciles a imputar. Hemos informado en el cuadro 1 que los deciles a corregir posiblemente son del I al VI, ya que en ellos se encuentran trabajadores de bajos ingresos, como: grupos étnicos, jornaleros o amas de casa, y de cierta forma constituyen un supuesto muy importante para elegir este escenario.
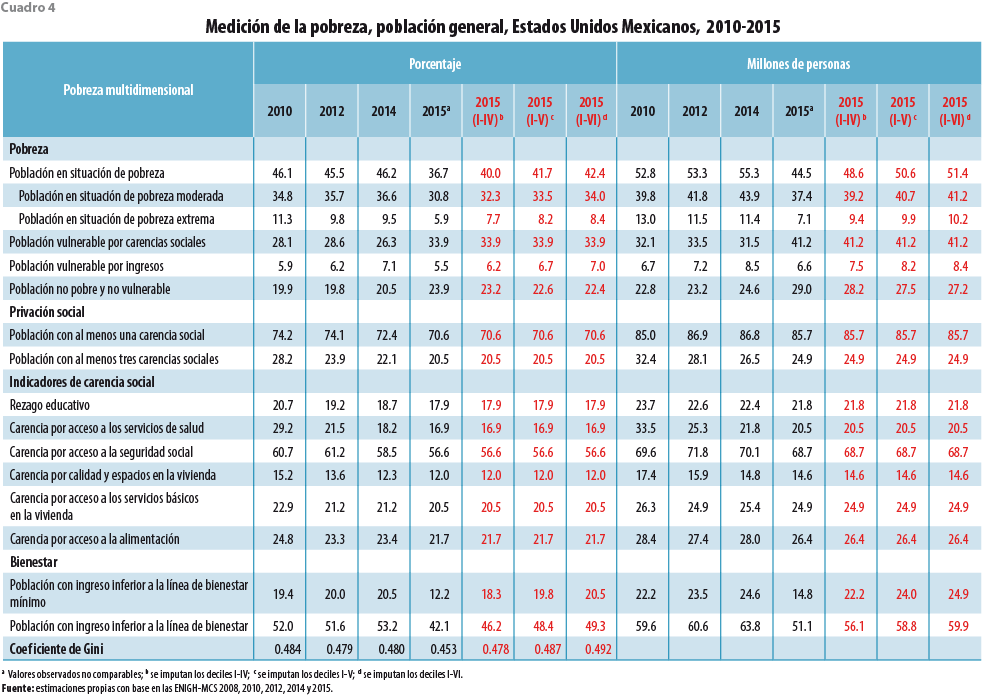
Los resultados para el escenario I-VI indican que la pobreza a nivel nacional es de 42.4% (51.4 millones de personas), una pobreza extrema de 8.4% (10.2 millones de personas) y un coeficiente de Gini de 0.492 (ver cuadro 4). Si tomamos este último escenario, los resultados son mixtos porque, por un lado, la pobreza se reduce (comparada con la incidencia del 2010 al 2014) pero, por el otro, la pobreza absoluta se mantiene como en el 2014. Por otra parte, el coeficiente de Gini se mantiene a la alza en este periodo, lo cual es un indicador de la inequidad en la distribución del ingreso.
Conclusiones
Existe un reto en la captación del ingreso por medio de encuestas; con frecuencia, éste se subestima o no se incluyen personas con ingresos altos. Hay varias formas de enfrentar este problema: los métodos de imputación pueden ser una vía útil para corregir esta dificultad y han sido extensamente utilizados. El presente artículo muestra una posible opción para hacer comparable la serie histórica del ingreso del 2010 al 2014 usando técnicas de imputación múltiple.
Todo modelo parte de supuestos y tendrá mejor desempeño si éstos se cumplen. Para realizar el presente ejercicio parte del supuesto de que el ingreso se vio afectado en los deciles inferiores de la distribución y, por lo tanto, un modelo que incorpore variables relacionadas con los estratos inferiores del ingreso podrá tener mejor capacidad para corregir este problema. Llamamos a este modelo de pobreza, ya que se especializa en medir con mayor precisión a la población con ingresos bajos y, en consecuencia, también se supone que los ingresos de los deciles superiores no fueron muy afectados. Quizá los ingresos altos tengan otro problema, que es el truncamiento, pero este caso está fuera de los objetivos del presente ejercicio.
Se estiman tres modelos de regresión (no se muestran) a través de los métodos de imputaciones múltiples, imputación vía regresión multivariada y FIML; los tres generan los mismos parámetros puntuales del modelo de regresión. Se selecciona el modelo de imputación múltiple y se generan tres escenarios: en el primero se eliminan los ingresos de los deciles I al IV; el segundo, los del I al V; y el tercero, los del I al VI para el MCS 2015.
De ellos, el tercero explica que los deciles I al VI muestran mayor distorsión en la captura del ingreso y, por lo tanto, se pueden corregir mediante imputaciones múltiples. Los resultados indican que la pobreza a nivel nacional es de 42.4%, que representa 51.4 millones de personas, una pobreza extrema de 8.4%, es decir, 10.2 millones de personas, y un coeficiente de Gini de 0.492.
_____
Fuentes
Arbuckle, J. L. “Full Information Estimation in the Presence of Incomplete Data”, in: Marcoulides, G. A. y R. E. Schumacker (eds.). Advanced Structural Equation Modeling: Issues and Techniques. Mahwah, New Jersey, Lawrence Erlbaum Associates, Inc., 1996, pp. 243-277.
Box, G. E. P. y G. M. Jenkins. Time Series Analysis: Forecastiong and Control. Englewood Cliffs, N. J., Prentice Hall, 1976.
Casella, G. y R. L. Berger. Statistical Inference (2nd ed.). Belmont, CA, Duxbury Advanced Series, 2001.
CONEVAL. “Metodología para la medición multidimensional de la pobreza en México”, en: Realidad, Datos y Espacio Revista Internacional deEstadística y Geografía.2(1). México, INEGI, 2011, pp. 36-63.
Enders, C. K. Applied Missing Data Analysis. New York, The Guilford Press, 2010.
Gelman, A.; J. B. Carlin; H. S. Stern y D. B. Rubin. Bayesian Data Analysis. (2nd ed.). New York, Chapman & Hall, 2004.
Gilks, W. R.; S. Richardson y D. J. Spiegelhalter. Markov Chain Monte Carlo in Practice. Washington, DC, Chapman & Hall-CRC, 1996.
Graham, J. W. y J. L. Schafer. “On the Performance of Multiple Imputation for Multivariate Data with Small Sample”, in: Hoyle, R. H. (ed.): Statistical Strategies for Small Sample Research. Thousands Oaks, CA., SAGE Publications, Inc., 1999, pp. 1-29.
Muthén, B.; D. Kaplan y M. Hollis. “On Structural Equation Modeling with Data That Are Not Missing Completely at Random”, in: Psychometrika. 52(3), 1987, pp. 431-462.
Ritter, C. y M. A. Tanner. “The Gibbs Stopper and the Griddy Gibbs Sampler”, in: Journal of the American Statistical Association. 87, 1992, pp. 861-868.
Roberts, G. O. “Convergence Diagnosis of the Gibbs Sampler”, in Bernardo, J. M.; J. O. Bergen; A. P. Dawid y A. F. M. Smith (eds.). Bayesian Statistics. Oxford University Press, 1992.
Rubin, D. B. Multiple Imputation for Nonresponse in Surveys. New York, USA, John Willey & Sons, 1987.
Russell, D. W.; H. S. Stern y S. Sinharay. An Evaluation of Multiple Imputation as an Approach to Missing Data. 2000.
Schafer, J. L. y J. W. Graham. “Missing Data: Our View of the State of the Art”, in: Psychological Methods. 7(2), 2002, pp. 147-177.
Schafer, J. L. y M. K. Olsen. “Multiple Imputation for Multivariate MissingData Problems: A Data Analyst’s Perspective”, in: Multivariate Behavioral Research. 33(4), 1998, pp. 545-571.
Shenker, N. y J. M. G. Taylor. “Partially Parametric Techniques for Multiple Imputation”, in: Computational Statistics & Data Analysis. 22, 1996, pp. 425-446.
Vargas Chanes, D. y F. O. Lorenz. “Inference with Missing Data Using Latent Growth Curves”, en: Revista del Instituto Interamericano de Estadística. 67(188 y 189), 2015, pp. 9-19.
_____
Anexo 1
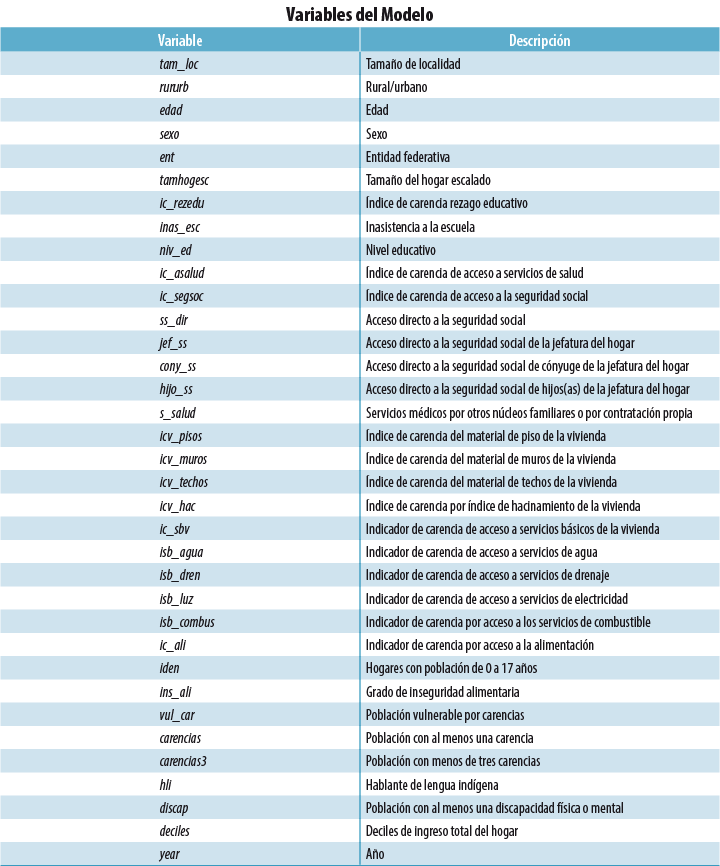
Variables del modelo El siguiente cuadro contiene las variables independientes que constituyen los modelos de imputación y de regresión:
Anexo 2

Anexo 3
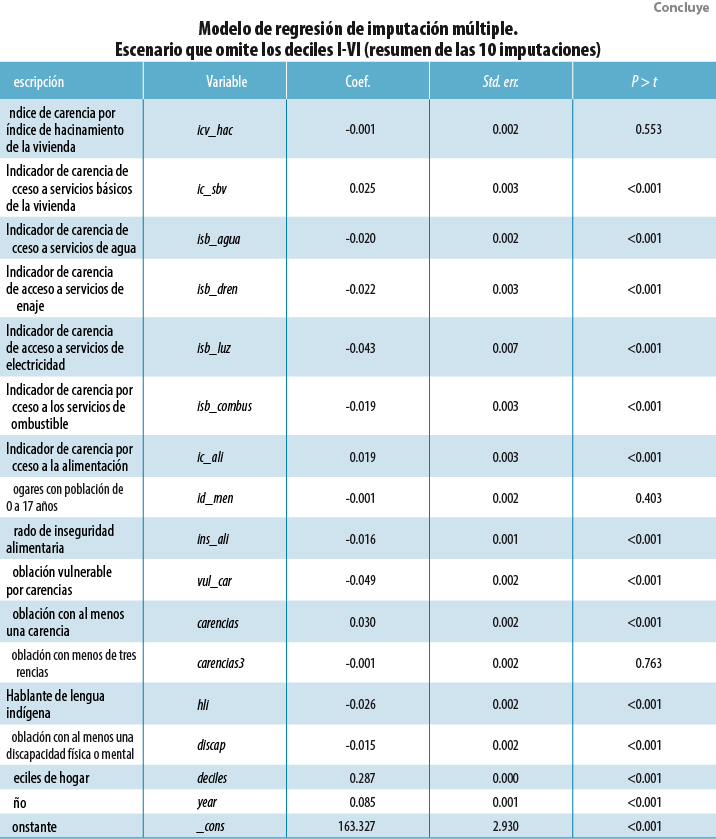
_____
1 Consideramos pertinente usar el ingreso de los hogares y no el ingreso per cápita al suponer que el primero es el que se vio más inflado durante el levantamiento del MCS 2015 para los deciles inferiores. Todos los ingresos en este ejercicio se deflactaron al 2015.
2 Las covariables incluyen aspectos sociodemográficos (sexo, edad, ocupación, escolaridad, jubilado), así como variables relacionadas con la pobreza (e. g., habla lengua indígena, carencia, rezagos sociales varios, tamaño del hogar, perceptores en el hogar, ocupados en el hogar, remesas, recibe ayuda de programas sociales).
3 La deflactación se hizo utilizando el índice nacional de precios al consumidor (INPC) de agosto de cada año; esta forma es la usada por el CONEVAL, que es congruente con lo propuesto en la metodología de medición multidimensional de la pobreza.
4 La base de datos con las covariables completas se tomaron del modelo de imputaciones múltiples, omitiendo los deciles I a VI del logaritmo del ingreso.
5 El valor 1 se asigna a los valores faltantes, que son el ingreso del hogar de los deciles I a VI y 0 si está presente; se usan 35 covariables que explican los valores faltantes (eliminados) en los deciles inferiores de la distribución del ingreso de hogares. El ajuste del modelo es satisfactorio y el supuesto de MAR se satisface.
6 Se han elegido m =10 imputaciones que garantizan una eficiencia relativa de 97 por ciento. La eficiencia relativa se calcula con la fórmula EF = (1– γ/m) –1, donde γ = 0.30 y m =10; es decir, se tiene 30% de información del ingreso faltante de los deciles I al VI al unir las dos bases de datos del 2014 y 2015.
7 El número de iteraciones de calentamiento (burn in iterations) se fija en mil para este ejercicio.
8 En este anexo se muestra el modelo ajustado para el escenario que omite los deciles I al VI.




