Identificación de la vegetación urbana de la Ciudad de México; evaluación de cuatro métodos para la determinación de umbrales en el índice normalizado de diferencias de vegetación y de la clasificación supervisada

 

Identification of Urban Vegetation in Mexico City; Assessment of Four Methods of Threshold Determination at Normalized Difference Vegetation Index and Supervised Classification

 

Enrique De Nova Vázquez, Germán Castro Ibarra y Humberto Ramos Ramos
 Instituto Nacional de Estadística y Geografía (INEGI), enrique.nova@inegi.org.mx, germancastro.ibarra@inegi.org.mx y humberto.ramos@inegi.org.mx, respectivamente

 

Vol.9, Núm.3 –  Epub                                                 Identificación de la vegetación… – Epub

 

En este trabajo se evalúan cuatro métodos de estratificación, dos criterios de determinación de umbrales en el índice normalizado de diferencias de vegetación y la clasificación supervisada (CS) en la identificación de la vegetación urbana de la Ciudad de México. Con el análisis exploratorio de datos (AED) y los algoritmos de estratificación Dalenius y Hodges (DH), Jenks y K-Medias (K-M) se obtuvieron umbrales cuyas precisiones totales fueron mayores a 96% al aplicar el criterio del promedio, más o menos una desviación estándar. Con el de cercanía al umbral obtenido por el AED (cuya precisión fue de 98.2% y un índice de Kappa de 0.962), los algoritmos DH y K-M tuvieron precisiones muy similares al anterior. Con el último, tanto la CS como el umbral identificado con el algoritmo de Jenks tuvieron diferencias significativas ( p < = 0.05) en la cuantificación de la vegetación urbana con respecto al AED, DH y K-M. Palabras clave: segmentación; análisis exploratorio de datos; Dalenius y Hodges; Jenks; K-Medias.

In this paper, four methods and two criteria of threshold determination were evaluated, as well as supervised classification, in order to identify urban vegetation in Mexico City. NDVI Thresholds were determined with Exploratory Data Analysis (EDA), Dalenius and Hodges (DH), Jenks and K-Means (K-M) algorithms and their total accuracies in urban vegetation identification were above 96% with the mean minus and plus a standard deviation criterion. With criterion of proximity to the threshold determined by EDA, which total accuracy was 98.2% and a Kappa Index of 0.962, DH and K-M algorithm accuracies were similar to previous criterion. With this last criterion, both supervised classification and the threshold defined with Jenks algorithm had significant differences ( p < = 0.05) at identification and computation of urban vegetation with respect to EDA, DH and K-M. Key words: segmentation; exploratory data analysis; Dalenius and Hodges; Jenks; K-Means.

Recibido: 20 de diciembre de 2017.
Aceptado: 19 de abril de 2018.

 

Introducción

Importancia de la vegetación urbana

En México, ocho de cada 10 personas viven en espacios urbanos. Procurar su bienestar requiere del entendimiento de distintos factores sociales y ambientales que pueden incidir en la salud de la población —como el acceso a los servicios públicos, de salud y a áreas verdes urbanas (Vlahov y Galea, 2002)—, de modo que sea posible diseñar medidas preventivas e intervenciones eficaces. Las áreas verdes urbanas (AVU) no son la panacea, pero sí parte sustantiva de un ambiente saludable. Su diseño, distribución, tamaño y accesibilidad influyen en el bienestar de la gente; además, existe evidencia empírica amplia que sostiene que la relación población-AVU propicia bienestar social, físico y psicológico. En suma, ofrecen diversos servicios ecosistémicos (Ayala, 2016; Sorensen et al. 1988).

Las AVU se han asociado al bienestar de la población urbana mediante varios mecanismos (Ayala, 2016; WHO, 2016; Ekkel y de Vries, 2017) como: mejoramiento de la calidad del aire, mortiguamiento del ruido y control de la temperatura, reducción del estrés, mejora de la actividad física y estímulo de beneficios sociales. Respecto al último, Meza y Moncada (2010) señalan que, además del esparcimiento y la recreación, las AVU ayudan en la reproducción cultural y al fortalecimiento de las relaciones sociales, refuerzan la identidad de barrios y colonias, además de que propician la tolerancia entre grupos y comportamientos diversos.

En contrapartida, las medidas preventivas e intervenciones deben considerar posibles efectos adversos asociados a las AVU (WHO, 2016); por ejemplo: el incremento de la exposición a la contaminación atmosférica, pesticidas y herbicidas; riesgos de alergias y asma; vectores de enfermedades e infecciones zoonóticas; radiación excesiva por exposición a los rayos ultravioleta; y vulnerabilidad ante delitos.

Todo lo anterior plantea el reto de crear y administrar un sistema de gestión integrado de las AVU con un enfoque de manejo de cuencas hidrográficas que contemplen parques públicos con componentes recreacionales y ecológicos, árboles en residencias y calles, proyectos de agricultura urbana y cinturones verdes (Sorensen et al., 1988). Considérese que la Ciudad de México (CDMX) padece desde hace tiempo la pérdida de áreas verdes, ya sea por reconversión a usos urbanos y agrícolas, malas prácticas y falta de vigilancia asociadas, además, a un seguimiento eficiente de las políticas ambientales y programas de ordenamiento territorial (Benítez, 1986). Núñez y Romero (2016) recomiendan el establecimiento de un sistema de monitoreo en el que se integre un inventario actualizado y homologado de las AVU con alcance metropolitano. Esto ya ha sido planteado con anterioridad; de hecho, la idea tiene más de 30 años sin que a la fecha se haya logrado su desarrollo.

Mapeo de la vegetación urbana utilizando percepción remota

La percepción remota satelital es una forma práctica y económica para estudiar la cubierta vegetal y sus cambios. Permite obtener observaciones sistemáticas en varias escalas espaciales, onsiderando distintos periodos. En un sentido amplio, la clasificación por medio de imágenes de satélite es un proceso a través del cual se extraen clases diferenciadas o categorías de uso del suelo a partir del procesamiento matemático de aquéllas (Xie et al. 2008).

Desde finales de la década de los 70, existen dos enfoques básicos para el procesamiento de imágenes satelitales con fines de clasificación (Roller, 1977). El primero, al que se denomina análisis de imágenes, incluye las técnicas de determinación de umbrales y segmentación de niveles para segregar una o varias categorías mediante la identificación de uno o varios umbrales a partir del nivel de intensidad de la radiación electromagnética registrada en una banda espectral.¹ También se incluye en este enfoque la obtención de una banda cociente (ratioining) como producto de la división entre dos bandas espectrales cuyas reflectancias se correlacionan, por lo general, de manera negativa. Posteriormente, a la banda cociente se le determina un umbral o varios para identificar a las clases o categorías de interés.

El segundo enfoque, llamado análisis numéricamente orientado, incluyó los métodos de clasificación no supervisada y supervisada, considerados por Xie et al. (2008) como los tradicionales para clasificar imágenes multiespectrales. Estos autores añaden al procesamiento los llamados métodos mejorados, que son algoritmos nuevos generados para resolver algunos problemas, ya sea de identificación de rasgos específicos o para reducir algunos efectos que generan determinados factores de confusión tanto tecnológicos como ambientales.

Los índices de vegetación (IV) pueden ser considerados como una derivación del primer enfoque propuesto por Roller (1977), ya que se generan con operaciones aritméticas (cocientes, diferencias o diferencias normalizadas) entre dos o más bandas espectrales (Ji et al., 2009; Muñoz, 2013). De manera similar a lo considerado por Xie et al. (2008) sobre los métodos tradicionales y mejorados de clasificación, los IV son clasificados como básicos o mejorados, es decir, estos últimos se han adecuado para resolver problemas específicos (Xue y Su, 2017). El uso de los IV requiere considerar las características propias del ambiente en el que se aplican, de ahí la existencia de una gran cantidad de ellos. Cada uno tiene su expresión de vegetación verde, es idóneo de acuerdo con los usos específicos para los que se creó y presenta ciertas limitantes.

Con los IV que combinan las longitudes de onda del espectro visible con el infrarrojo cercano se ha mejorado significativamente la detección de la vegetación y, aun cuando hay muchas consideraciones sobre las complicaciones que representa su uso, la construcción de un IV simple puede ser una herramienta efectiva para medir el estado de la vegetación (Xue y Su, 2017).

Debido sobre todo a la fotosíntesis y al contenido de humedad, las plantas presentan un comportamiento contrastante con respecto a la interacción que tienen con las longitudes de onda del infrarrojo cercano y del rojo: mientras que la primera la reflejan en mayor medida, absorben la mayor parte de la segunda (Xie et al., 2008). Esta interacción fue la que aprovecharon Rouse et al. (1974) en la combinación de las bandas espectrales 7 y 5 del sensor MSS de Landsat para detectar biomasa verde y proponer al índice normalizado de diferencias de vegetación (NDVI, por sus siglas en inglés) como parte de un sistema de monitoreo de vegetación. En la actualidad, éste es el IV más utilizado por su alta capacidad para detectar vegetación incluso en áreas con poca cobertura, aunque sea sensible a los efectos del brillo y color del suelo, a los atmosféricos, de las nubes y sus sombras, así como a las sombras que provoca el dosel. El NDVI se calcula con la siguiente ecuación:

NDVI = (IRc – R) / (IRc + R)

donde:

NDVI = índice normalizado de diferencias de vegetación.
IRc = longitud de onda del infrarrojo cercano.
R = longitud de onda del rojo.

El uso del NDVI involucra la determinación de un umbral (o varios) para identificar los rasgos de interés, lo cual es un paso crítico que requiere de un criterio sólido que permita segmentar la imagen de manera satisfactoria (Chuvieco, 2002), y es un procedimiento común en la estratificación y agrupación de datos. Se busca clasificar dos o más grupos de manera que exista cohesión al interior del grupo y cierto aislamiento entre ellos; en otras palabras, por medio de los cientos de métodos de agrupación que hay se pretende estructurar los datos de tal manera que sea posible su clasificación. Dado lo anterior, la aplicación de estas técnicas debe incluir siempre la evaluación de su eficacia (Milligan y Cooper, 1987).

Las estimaciones de vegetación con el NDVI son consideradas como una forma de medir la disponibilidad de áreas verdes que tiene la población en zonas urbanas (WHO, 2016). En este sentido, se han realizado diversos estudios para incorporar a este IV en la investigación de la relación vegetación urbana-bienestar social. Desafortunadamente, los investigadores rara vez reportan los métodos de determinación de umbrales e, incluso, los umbrales mismos. Menos aún se reporta la eficacia de ellos en la detección de vegetación (Moreira y Zerda, 1999; Peña et al., 2008; Rhew et al., 2011; Amoly et al., 2014, Ekkel y de Vries, 2017). También es frecuente que éstos se reporten de manera muy general, sin consideraciones respecto a la forma en la que ello afecta a los errores de omisión o comisión que pueden verse incrementados (Chuvieco, 2002), lo cual repercute en el cálculo del área de vegetación detectada.

Con el empleo de los estadígrafos básicos de un grupo de datos y de técnicas básicas de despliegue de los mismos, el AED permite detectar cambios sutiles definidos como umbrales. Con esto se incrementa la capacidad para reconocer patrones (Huber, 2016). Los detectados con el AED pueden ser confirmados (Church, 1979) con algún otro método de agrupación o estratificación, de preferencia que sea accesible, como es el caso de los algoritmos de Jenks, Dalenius y Hodges y K-Medias.

Los objetivos del presente estudio fueron: a) generar un procedimiento de determinación de umbrales que incluya dos criterios de elección de los mismos, utilizando los valores del NDVI y empleando el análisis exploratorio de datos (AED) y tres algoritmos de estratificación (Jenks, Dalenius y Hodges y K-Medias) y b) evaluar los umbrales de segmentación del NDVI determinados en la identificación, cuantificación y mapeo de la vegetación urbana de la Ciudad de México.

Metodología

Área de estudio

La Ciudad de México se localiza entre las coordenadas extremas 19° 35’ 34” y 19° 2’ 54” de latitud Norte y -98° 56’ 25” y -99° 21’ 54” de longitud Oeste (ver imagen 1). Su altitud media es de 2 311 metros sobre el nivel del mar (m.s.n.m.) y la máxima corresponde al cerro de la Cruz del Marqués con 3 930 m.s.n.m.

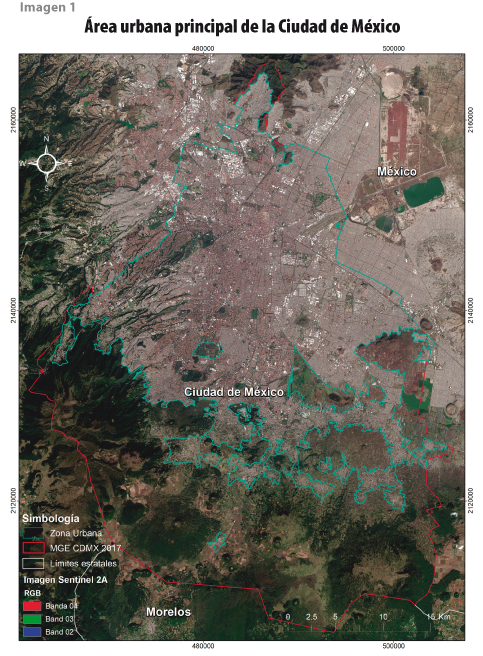
De acuerdo con la clasificación de los climas de Köppen modificada por Enriqueta García (2004), el dominante es el templado subhúmedo con lluvias en verano en casi 60% de la superficie de la entidad, seguido del semifrío subhúmedo, presente en 33.5% del territorio en las partes altas de la zona sur-suroeste. El semiseco templado corresponde a una pequeña porción al noreste del estado. La temperatura media anual, dependiendo de los tipos de clima, oscila entre los 9.7 y los 16.9 grados Celsius. La precipitación total anual varía entre 609 y 1 259.9 milímetros.

Los principales grupos de vegetación presentes son los bosques templados de coníferas y latifoliadas, predominantes al sur; pastizales y áreas de cultivos anuales en la zona sur y sureste, así como matorrales en algunos relictos de la Sierra de Guadalupe al norte y en la Reserva del Pedregal por el centro (INEGI, 2016). Las áreas cubiertas de vegetación natural o inducida (áreas verdes) incluyen bosques urbanos, parques, jardines, plazas con jardines, árboles o jardineras, zonas de la vía pública y azoteas con cubierta vegetal, alamedas, arboledas y otras áreas análogas (PAOT, 2014)

El estudio se realizó sobre el área urbana principal de la Ciudad de México, cuyos límites se ajustaron visualmente a partir del archivo vectorial obtenido del Marco Geoestadístico Urbano del 2016 (INEGI, 2017). Con este ajuste se descartaron las áreas correspondientes a distintas zonas con cobertura vegetal densa y sin presencia de rasgos urbanos; se eliminaron de la evaluación esos espacios para enfocarse en la detección de la vegetación mezclada con áreas urbanas (ver imagen 1). La mancha urbana delimitada incluye las zonas centro y norte, y representa poco menos de 50% de la superficie de la Ciudad de México. El resto es prácticamente suelo de conservación con poco o nada de urbanización.

Imagen de satélite y software

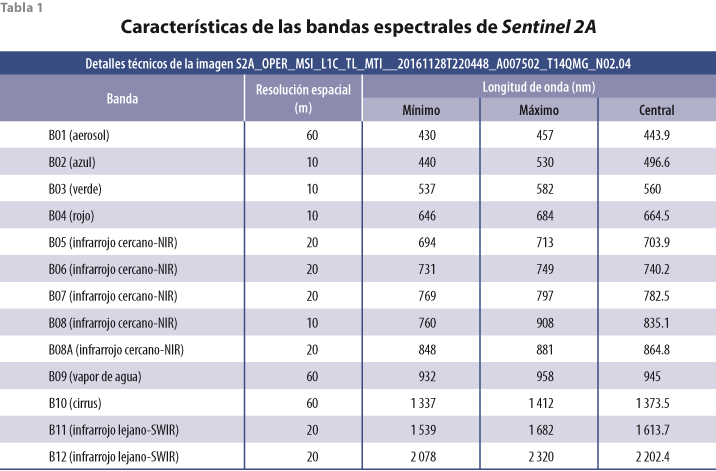
La imagen que se utilizó para el proceso de clasificación es una Sentinel 2A, con un nivel de procesamiento 1C, el cual proporciona información ortorrectificada en cuadros o Tiles de 100 x 100 km² con proyecciones UTM-WGS84 por zona (Baillarin et al., 2012). La toma se realizó el 28 de noviembre de 2016 a las 17:06:42 horas, con el identificador de los datos GS2A_20161128T170642_007502_N02.04 en formato JPEG2000 y resolución espacial de 10 metros por pixel para las bandas espectrales 2, 3, 4 y 8; 20 metros para las 5, 6, 7, 8A, 11 y 12; y 60 metros para las 1, 9 y 10 (ver tabla 1). La imagen es un producto tipo S2MSI1C con una cobertura de nubes de 0.2% que no abarcan el área de estudio.

La imagen se descargó del sitio web de la Agencia Espacial Europea Copernicus Open Access Hub (https://scihub.copernicus.eu/dhus/#/home). El procesamiento de los datos se realizó con ArcGIS Desktop10.5, Mapa Digital de México 6.3.0 y Excel.

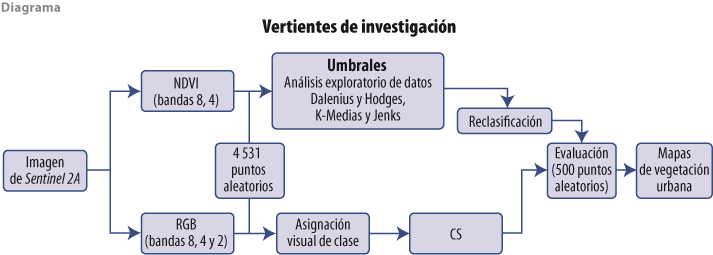
Diagrama de flujo para mapear la vegetación urbana utilizando imágenes de Sentinel 2A

El trabajo de investigación siguió dos vertientes: 1) considerando al NDVI y los distintos métodos de determinación de umbrales y 2) tomando en cuenta la imagen compuesta con las bandas espectrales 8, 4 y 2 y la clasificación supervisada (CS). Ambas confluyeron en las evaluaciones con muestras independientes para cada método (ver diagrama).

Determinación de umbrales y CS

Análisis exploratorio de datos (AED)

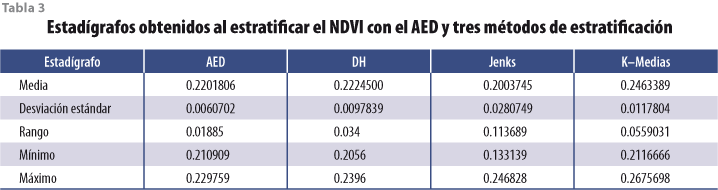
Con apoyo de la imagen compuesta por las bandas espectrales 8, 4 y 2 (que corresponden al infrarrojo cercano, al rojo y al azul, respectivamente) se identificaron en 4 531 puntos rasgos urbanos, agua y vegetación. Los primeros agruparon al suelo desnudo, espacios pavimentados, techos de edificios, áreas industriales y habitacionales, así como vialidades. Dentro de la categoría de vegetación se agrupó la zona boscosa del suelo de conservación, el arbolado urbano, los pastos y herbáceas, jardines y vegetación hidrófila. En el rasgo agua se identificaron visual y estadísticamente dos tipos: uno correspondiente al agua como tal y otro al agua con florecimientos. La agrupación se realizó con base en los estadígrafos de los valores del NDVI de cada rasgo (ver tabla 2). Los correspondientes al agua con florecimientos fueron muy altos y, por lo tanto, se ubicaron entre los valores de vegetación. Este grupo de cuerpos de agua se compone por los lagos Nabor Carrillo y Chalco, así como por las lagunas de Xico, que se ubican fuera del área de estudio (ver imagen 1). Por esta misma razón, el lago menor de Chapultepec y el lago del Parque Tezozómoc (ambos se encuentran dentro del área urbana principal) fueron identificados como vegetación.

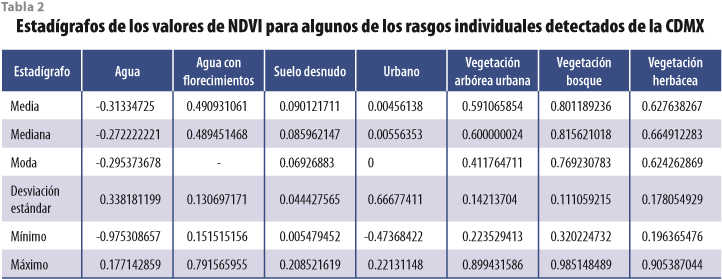
A cada uno de los 4 531 puntos se les asignó el valor correspondiente del NDVI para realizar tanto el AED como la determinación de umbrales con los diferentes métodos. Se revisaron los datos atípicos y se ajustaron los valores al intervalo -1 > NDVI < 1. El AED se realizó con el análisis visual de la gráfica de dispersión, lo cual permitió detectar 24 puntos cuyos valores se encontraban entre los rasgos urbanos, del agua y la vegetación; con estos valores se generaron los estadígrafos correspondientes al AED de la tabla 3. Dado que el fin último del trabajo fue la identificación de la vegetación urbana y que el AED permitió agrupar a los valores de NDVI de los distintos rasgos, la determinación de umbrales se realizó específicamente para separar a los rasgos urbanos de la vegetación.

Determinación de umbrales con los algoritmos de clasificación-estratificación

Se empleó la clasificación de campos numéricos para la simbología graduada (clasificación-estratificación) en la determinación de los umbrales de los mismos puntos analizados en el AED, pero empleando los algoritmos de Jenks del programa ArcGIS y K-Medias y Dalenius y Hodges (DH) del programa Mapa Digital de México.

Se estratificaron los 4 531 puntos con cada uno de los algoritmos, realizando desde dos hasta 20 estratificaciones, para tener valores con los cuales estimar los estadígrafos correspondientes de la tabla 3, considerando que la identificación de categorías o estratos tiene sentido interpretativo hasta una cantidad de 15. De los estratos se eligieron los valores de clase más próximos al determinado por el AED para la generación de los estadígrafos. Estos valores fueron útiles en la determinación de los umbrales del NDVI que separan a los rasgos de vegetación de los urbanos.

Se determinaron los umbrales considerando dos criterios: uno fue el promedio, más o menos una desviación estándar; el segundo consistió en identificar identificar el valor de los estadígrafos más cercano al determinado con el AED. Con éste, para el algoritmo de Jenks, se determinó el valor medio y para el algoritmo de K-Medias se consideró el mínimo de los estadígrafos.

Clasificación supervisada

Se realizó con el algoritmo de máxima verosimilitud (MLC, por sus siglas en inglés) del programa ArcGIS considerando los 4 531 puntos aleatorios y solamente dos clases (urbano y vegetación) con el fin de comparar los métodos de segmentación con este método, que es el que se emplea con más frecuencia. Una vez aplicada la CS considerando la imagen compuesta (bandas espectrales 8, 4 y 2) y determinados los umbrales en los valores del NDVI con los cuatro métodos, se aplicó una reclasificación con el programa de ArcGIS, de manera que solo se representaran pixeles urbanos o de vegetación en los mapas generados.

Matrices de error y coeficiente de Kappa

A los archivos obtenidos en los que se identificaron la vegetación y los rasgos urbanos, tanto por la CS como por los umbrales determinados con los cuatro métodos, se les evaluó su precisión con matrices de error y con el estadístico de Kath, el cual es una estimación del de Kappa. El primero se calcula con:

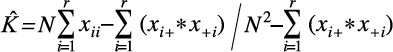
Las matrices son un arreglo de hileras y columnas que expresan el número de unidades de muestreo (pixeles) asignados a una categoría en particular y en relación con la categoría real verificada en el terreno o con otros métodos, como el uso de imágenes de mayor resolución espacial. Las columnas representan a los datos de referencia, mientras que las hileras señalan a los datos obtenidos con la clasificación (Congalton, 1991).

Con las matrices de error se obtiene la precisión total del productor (errores de omisión) y la del usuario (errores de comisión). La primera se calcula dividiendo la suma total de los datos correctos, es decir, la suma de los valores de la diagonal mayor de la matriz entre el número de pixeles de la matriz de error. En la segunda se consideran las columnas, dividiendo la magnitud observada de la categoría entre el número total de esa categoría, es decir, el total de la columna. La tercera se determina con los datos de las hileras, dividiendo la cantidad correcta de esa categoría entre el total de la hilera. En este caso, los datos para la matriz se generaron con la contabilidad de las categorías vegetación y urbano, definidas en función de los umbrales de cada método de segmentación en el NDVI y cotejadas en la imagen compuesta con las bandas 8, 4 y 2, donde la vegetación se resalta en rojo y sobre 500 puntos aleatorios generados por prueba, es decir, a partir de muestras independientes.

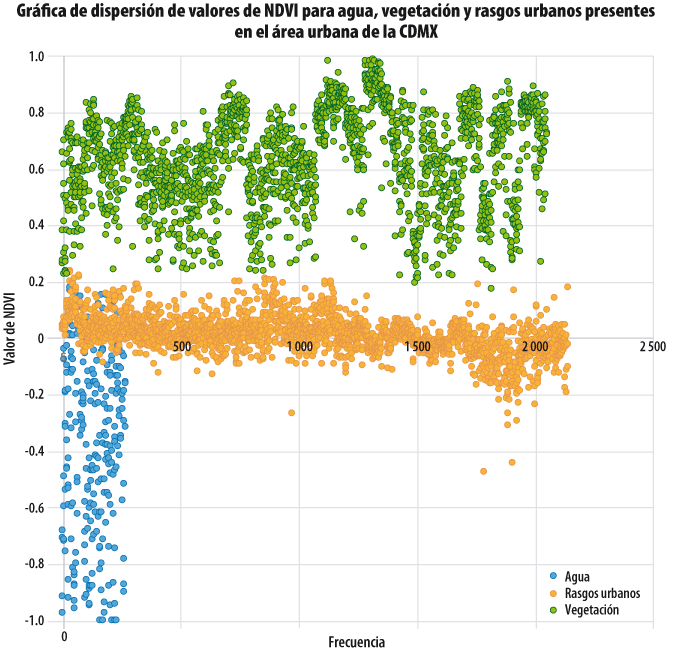
Además de ser una medida de precisión de la identificación de rasgos, el estadístico de Kath es también una técnica robusta que proporciona información acerca de una matriz e igual permite la comparación estadística de matrices (análisis de Kappa). Así, se realizaron pruebas de significancia estadística del valor de Kath mediante el análisis Kappa para identificar diferencias entre los distintos métodos y umbrales evaluados de acuerdo con Cohen (1960) y Fleiss et al. (1979). Se evaluó la concordancia entre la clasificación de rasgos urbanos y vegetación generada con los distintos métodos y umbrales determinados. Estas pruebas fueron posibles dado que el estadístico de Kath se distribuye normalmente. La ecuación para la comparación de índices de Kappa es:

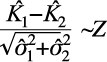
Resultados y discusión

Umbrales identificados considerando el criterio del promedio, más o menos una desviación estándar y el criterio de cercanía al valor determinado por el AED

Tomando en cuenta el criterio del promedio, más o menos una desviación estándar, el cual es empleado con mayor frecuencia para determinar umbrales (Chuvieco, 2002) y que se calculó a partir de los estadígrafos básicos de la tabla 3, se observa (ver tabla 4) que los cuatro métodos permitieron una determinación de umbrales del NDVI muy similar, es decir, que presentan diferencias mínimas entre sí. Todos los umbrales pueden considerarse satisfactorios, dado que la precisión total de la clasificación fue de 98.2% para el AED, 97.8% para el algoritmo DH y mayor de 96% para los algoritmos de Jenks y K-Medias.

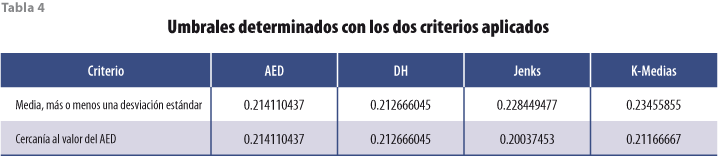
Dada la alta precisión en la clasificación por parte del AED, se consideró el criterio de la cercanía al valor determinado por este método como valor de referencia para elegir los umbrales con los algoritmos de DH, de Jenks y K-Medias. Para el DH, el valor fue el mismo, pero no para el de Jenks ni para el de K-Medias (ver tabla 4), cuyos valores fueron el promedio y el valor mínimo, respectivamente. Los umbrales determinados con este criterio fueron satisfactorios para los algoritmos DH y K-Medias, ya que la exactitud en la clasificación fue de 98.2 y 95.2, en ese orden, pero no fue igual de satisfactorio para el de Jenks, dado que se obtuvo una precisión total de la clasificación de 89.6% (ver tabla 6).

Mapeo de la vegetación urbana

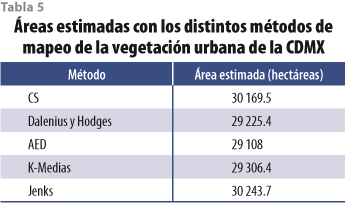
La vegetación estimada (considerando el umbral determinado por los distintos métodos y el criterio del valor más cercano al AED) se observa en la tabla 5. Considerando la superficie identificada con el umbral del AED, las AVU representan 38.8% ± 1.3% del área urbana de la Ciudad de México. El valor de 1.3% significa la diferencia de casi mil hectáreas que se detectaron con la CS y el umbral determinado con el algoritmo de Jenks, en comparación con el AED, DH y K-Medias.

La sobreestimación de las superficies de vegetación por la CS y el algoritmo de Jenks se observa en la imagen 2. Con la primera, ésta sucedió de manera zonal (comparación AED vs. MLC), en tanto que con el algoritmo se presentó de manera difusa y homogénea en toda el área de estudio (comparación DH vs. Jenks).

Evaluación de los umbrales identificados con el criterio de cercanía al umbral determinado por el AED

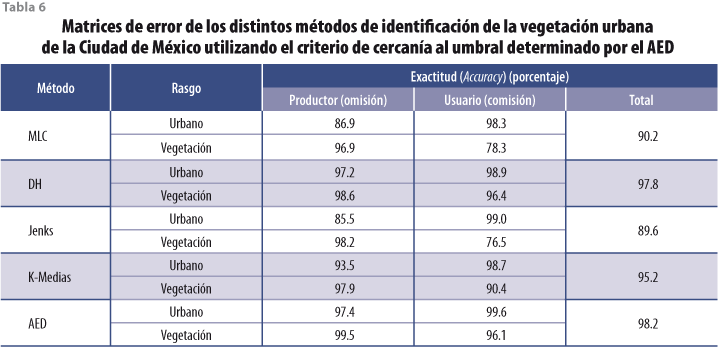
Con los distintos umbrales del NDVI de la tabla 4 (segundo criterio), más la CS (con el algoritmo de MLC) y su cotejo con la clasificación visual, se generaron generaron las matrices de error que se anotan en la tabla 6. Los valores relativamente altos de exactitud total de la clasificación alcanzada por todos los métodos y sus umbrales podrían considerarse como satisfactorios y muy satisfactorios. No obstante, para el caso de la CS y el algoritmo de Jenks, los errores de omisión y de comisión señalan que, aunque 96.9 y 98.2% (exactitud del productor) de las áreas de vegetación han sido identificadas por estos métodos, solamente 78.3 y 76.5% (exactitud del usuario), respectivamente, de esas áreas corresponden en realidad a vegetación urbana, lo que significa una disminución en la identificación del rasgo de interés del estudio.

De acuerdo con Congalton (1991), la exactitud del productor indica la probabilidad de que un pixel de referencia sea clasificado correctamente y la del usuario señala la probabilidad de que un pixel clasificado en la imagen en realidad represente a la categoría en el terreno. Dado que con el resto de las técnicas se obtuvieron diferencias porcentuales relativamente pequeñas entre sus correspondientes exactitudes de productor y de usuario, y que los valores fueron mayores a 95% para la mayoría de los métodos en ambos tipos de exactitud, se puede decir que éstos clasificaron muy bien a la vegetación; en otras palabras, el AED y los algoritmos DH y K-Medias la identificaron de una manera muy confiable.

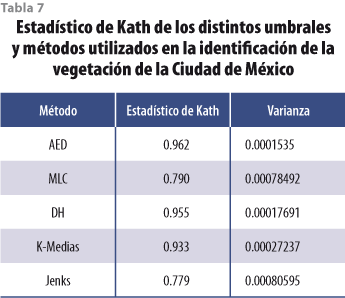
El estadístico de Kath (ver tabla 7) confirma lo asentado en el párrafo que antecede: es otra medida de la exactitud de la clasificación y señala la posibilidad de que lo observado haya ocurrido o no por azar. En ese sentido, el AED, los algoritmos DH y K-Medias aplicados al NDVI concordaron en más de 93% con la clasificación realizada visualmente, y la concordancia de la CS y el algoritmo de Jenks fue menor de 80 por ciento.

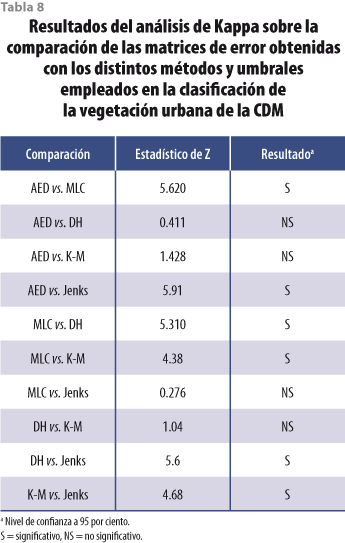
La comparación de las matrices de error mediante el índice de Kappa utilizando su estimador, que es el estadístico de Kath (ver tabla 8), indica que la CS y el algoritmo de Jenks identificaron de manera similar a la vegetación urbana de la Ciudad de México y que esta identificación fue significativamente diferente a los otros métodos utilizados, los cuales también tuvieron, en cuanto a la clasificación, un resultado similar entre sí.

Las diferencias observadas de los distintos métodos con respecto a la CS tal vez se deban a que el algoritmo de MLC requiere que los datos presenten una distribución normal, y esto no fue así, de acuerdo con el análisis del histograma de los datos utilizados para la clasificación. Además, incluye iteraciones en las que se afinan las firmas espectrales con el fin de aumentar la precisión en la identificación de rasgos y eso no se realizó en este trabajo.

Las diferencias observadas por los distintos métodos se reflejaron en el área estimada de la vegetación (ver tabla 5). Con la CS y el algoritmo de Jenks se sobreestimaron alrededor de mil hectáreas con respecto a las demás técnicas y, dado que estos dos métodos tuvieron los mayores errores de usuario, se puede afirmar que las mil hectáreas fueron mal identificadas.

Discusión general

El proceso para determinar umbrales en este trabajo siguió una ruta mixta, como lo sugieren Schiewe (2002) y Khan (2014). Por un lado, con el AED se calculó el del NDVI de manera supervisada como parte de un enfoque derivado de la imagen (Dey et al., 2010), es decir, considerando los estadígrafos de los 4 531 puntos aleatorios y, por el otro, la identificación de los umbrales por las técnicas de Dalenius y Hodges, Jenks y K-Medias representa una segmentación no supervisada también sugerida por los datos y la lógica de agrupación de cada uno de los métodos.

El criterio de elección del valor más cercano al determinado por el AED también fue adecuado cuando los umbrales fueron generados con los algoritmos de Dalenius y Hodges y K-Medias, no así cuando fue elegido con el de Jenks. Lo anterior refuerza la necesidad de evaluar tanto a los umbrales como a los algoritmos con métodos como las matrices de error y el estadístico de Kath (Havasova et al., 2015) lo que, a su vez, permite elegir umbrales óptimos y al algoritmo más adecuado al aplicar al análisis de Kappa.

Los umbrales determinados del NDVI muestran diferencias sutiles que se reflejan en la identificación y estimación del área de vegetación. Esto sugiere que, además de un criterio sólido de segmentación, también se requiere de un método sólido de segmentación en el que se incluya al AED y la evaluación de los umbrales determinados. Además de la pequeña diferencia observada entre los valores de los umbrales, es probable que el número de dígitos empleados también influya en la identificación y estimación del área de vegetación, tal como lo señalan Xie et al. (2010), quienes en la identificación de la vegetación de cuerpos de agua (oasis) en China con diferentes métodos de segmentación encontraron que “…un ligero cambio en el valor del umbral resulta en cambios abruptos inesperados…” en la detección de vegetación.

De acuerdo con Tilton et al. (2015), no existe una teoría general para la segmentación de imágenes, y la mayoría de los enfoques son ad hoc por naturaleza. Además, no hay un algoritmo general que funcione bien para todas las imágenes; ello, tal vez, porque el resultado de la segmentación tiene una dependencia multifactorial (Khan, 2014). Lo anterior permite confirmar que en el uso del NDVI para identificar vegetación urbana es crucial la determinación de umbrales óptimos y que las recomendaciones de umbrales determinados habrá que evaluarlas y no darlas por sentado.

Conclusiones

El AED y el algoritmo de Dalenius y Hodges no presentaron diferencias estadísticas significativas en la determinación de umbrales del NDVI considerando los dos criterios señalados: el promedio, más o menos una desviación estándar y la cercanía al valor determinado por el AED. Tomando en cuenta los porcentajes de las matrices de error, con ambos métodos de determinación de umbrales se obtuvieron resultados muy satisfactorios en la identificación y cuantificación del área de la vegetación urbana de la Ciudad de México. También se obtuvieron resultados muy satisfactorios con los algoritmos de clasificación K-Medias y Jenks, considerando el criterio del promedio, más o menos la desviación estándar. Los diferentes métodos empleados más el criterio de la cercanía al umbral determinado por el AED arrojaron resultados diferentes. Así pues, el criterio de cercanía al umbral determinado por el AED debe tomarse con precaución.

El procedimiento identificado para determinar umbrales puede seguir los pasos que se enuncian a continuación:

1) AED de puntos aleatorios a los que se les ha asignado el valor del NDVI correspondiente.
2) Identificación de umbral de separación de la vegetación con respecto a los rasgos urbanos mediante el mismo AED y con las estadísticas básicas de los valores límites de clase de los estratos identificados con los algoritmos de Dalenius y Hodges, Jenks y K-Medias, más o menos una desviación estándar.
3) Evaluación de los umbrales de segmentación con matrices de error y el índice de Kappa.

Con este procedimiento se puede realizar un monitoreo general y apoyar en la creación de un sistema de información geográfica de áreas verdes urbanas que facilite la gestión de las mismas en la Ciudad de México. Para identificar con más detalle la fisonomía de los diferentes tipos de vegetación, es recomendable seguir ensayando con distintos índices de vegetación y con distintos umbrales.

___________

Fuentes

Amoly, E., D. Payam, J. Forns, M. López-Vicente, X. Basagaña, J. Julvez, M. Álvarez-Pedrerol, M. Nieuwenhuijsen and J. Sunyer. “Green and blue spaces and behavioral development in Barcelona schoolchildren: The Breathe Project”, en: Environmental Health Perspectives. Vol. 122 (12). EE.UU., Editorial EHP, 2014, pp. 1351-1358 (DE) bit.ly/3Wd8tls, consultado el 15 de agosto de 2017.

Ayala, C. “Extrañarás los árboles”, en: Nexos. México, junio 28 de 2016 (DE) bit.ly/3S9pBYj, consultado el 17 de junio de 2017.

Baillarin, S., A. Meygret, C. Dechoz, B. Petrucci, S. Lacherade, T. Tremas, C. Isola, P. Martimort and F. Spoto. “Sentinel-2 Level 1 Products and Image Processing Performances”, en: International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences. XXII ISPRS Congress Volume XXXIX-B1. Australia, 2012, pp. 197-202 (DE) bit.ly/3WtQmcD, consultado el de 3 de junio de 2017.

Benítez, B. “Áreas verdes en una ciudad en explosión: el caso de la Ciudad de México”, en: Seminario Internacional sobre el Uso del Suelo, Tratamiento y Gestión del Verde Urbano. España, MAB-UNESCO, 1986, pp. 101-110.

Cohen, J. “A coefficient of agreement for nominal scales”, en: Educational and Psychological Measurement. Vol XX., no. 1, 1960, pp. 37-46.

Congalton, R. “A review of assessing the accuracy of classifications of remotely sensed data”, en: Remote Sensing of Environment. 37, 1991, pp. 35-46 (DE) bit.ly/3Y5i0xL, consultado el 5 abril de 2017.

Chuvieco, E. Teledetección ambiental. España, Editorial Ariel Ciencia, 2002, 447 p.

_______ Fundamentos de teledetección espacial. Madrid, España, Ediciones Rialp, SA, 1995, 449 p.

Church, R. “How to look at data: A review of John W. Tukey´s exploratory data analysis”, en: Journal of the Experimental Analysis of Behavior. 31(3). EE.UU., Brown University, 1979, pp. 433-440 (DE) bit.ly/3WaAMkL consultado el 13 de mayo de 2017.

Dey, V., Y. Zhang and M. Zhong. “A review on image segmentation techniques with remote sensing perspective”, en: Wagner, W. y B. Székely (eds.). ISPRS TC VII Symposium: 100 Years ISPRS. Vienna, Austria, July 5-7, 2010, IAPRS, Vol. XXXVIII, Part 7A, ISPRS Technical Commision (DE) bit.ly/3LuCo3L, consultado el 6 de abril de 2018.

Ekkel, E. and S. de Vries. “Nearby green space and human health: evaluating accessibility metrics”, en: Landscape and Urban Planning. 2017, pp. 2014-2020 (DE) bit.ly/4cLTfee, consultado el 20 de junio de 2017.

ESRI. ArcGIS Desktop 10.5. Redlands, CA, Environmental Systems Research Institute, 2016.

Fleiss, J., J. Cohen and B. Everitt. “Large simple standard errors of Kappa and weighted Kappa”, en: Psychological Bulletin. Vol. 72(5), 1969, pp. 323-327 (DE) www.researchgate.net/publication/200656845LargeSampleStandardErrorsofKappaandWeightedKappa,
consultado el 23 de mayo de 2017.

García, E. Modificaciones al sistema de clasificación climática de Köppen (para adaptarlo a las condiciones de la República Mexicana). Serie Libros, Quinta Edición, Instituto de Geografía-UNAM, 2004, 90 p.

Havasova, M., T. Bucha, J. Ferencík and R. Jakus. “Applicability of a vegetation indices-based method to map bark beetle outbreaks in the High Tatra Mountains”, en: Annals of Forest. Research. 58(2). Rumania, Ilfov, 2015, pp. 295-310 (DE) bit.ly/4cJS1jX, consultado el 6 de abril de 2018.

INEGI. Marco Geoestadístico. México, Instituto Nacional de Estadística y Geografía, 2017 (DE) bit.ly/4bRq6xc, consultado el 1 de septiembre de 2017.

_______ Anuario estadístico y geográfico de la Ciudad de México. México, Instituto Nacional de Estadística y Geografía, 2016, 514 p.

_______ Mapa Digital de México para escritorio 6.3.0. INEGI, Aguascalientes, México, 2017.

Huber, G. “La aportación de la estadística exploratoria al análisis de datos cualitativos”, en: Perspectiva Educacional. Formación de Profesores. Chile, 2016, 24 p. (DE) bit.ly/3ScdZUi, consultado el 15 de octubre de 2017.

Ji, L., L. Zhang and B. Wylie. “Analysis of dynamic thresholds for the normalized difference water index”, en: Photogrammetric Engineering & Remote Sensing. Vol. 75, no. 11. American Society for Photogrammetry and Remote Sensing, 2009, pp. 1307-1317 (DE) bit.ly/4f6dyVx, consultado el 1 de septiembre de 2017.

Khan M.W. “Image Segmentation Techniques: A survey”, en: Journal of Image and Graphics. Vol. 1, no. 4, December 2013 (DE) bit.ly/46cntor, consultado el 6 de abril de 2018., consultado el 6 de abril de 2018.

Meza, M. y J. Moncada. “Las áreas verdes de la ciudad de México. Un reto actual”, en: Scripta Nova. Geocrítica Revista Electrónica de Geografía y Ciencias Sociales. Vol. XIV, núm. 331 (56). España, Universidad de Barcelona, 2010, s/p (DE) bit.ly/3ScEOrw, consultado el 8 de agosto de 2017.

Milligan, G. and M. Cooper. “Methodology review: Clustering methods”, en: Applied Psychological Measurement. Vol. 11(4). EE.UU., Digital Conservancy at the University of Minnesota, 1987, pp. 329-354 (DE) bit.ly/4bPeaMp, consultado el 6 de agosto de 2017.

Moreira, M. y H. Zerda. “Mapeo de áreas verdes en ambientes urbanos mediante datos SPOT e índices de vegetación”, en: 1.ras jornadas de SIG para la Evaluación de Recursos Naturales, el Agroambiente y la Planificación Rural. Argentina, INTA-UNSE, Santiago del Estero, 1999, pp. 18-19 (DE) bit.ly/3yei2bT consultado el 3 de agosto de 2017.

Muñoz, A. Apuntes de teledetección: Índices de Vegetación. Chile, CIREN, 2013 (DE) bit.ly/3YatMXM, consultado el 12 de agosto de 2017.

Nuñez, J. y M. Romero. “Imperativos para una ciudad sustentable: áreas arboladas y planeación territorial”, en: Mohar, A. (coord.). Tendencias territoriales determinantes del futuro de la Ciudad de México. México, CentroGeo, 2016, pp. 311-339.

Peña, O., G. Ostertag, R. Gandullo y A. Campo. “Comportamiento de la vegetación de un humedal (Mallín) entre periodos húmedos y secos mediante análisis meteorológico y espectral”, en: Boletín Geográfico. Año XXX, núm. 31, edición especial: VII Jornadas Patagónicas de Geografía. Argentina, Departamento de Geografía, Universidad Nacional del Comahue, 2008, pp. 93-105 (DE) bit.ly/3YaOp66, consultado el 5 de agosto de 2017.

Procuraduría Ambiental y del Ordenamiento Territorial. Áreas verdes urbanas del Distrito Federal: elementos básicos. México, PAOT, 2014, 134 p. (DE) bit.ly/4d6bhb3, consultado el 26 de agosto de 2018.

Rhew, I., S. Vander, A. Kearney, N. Smith and M. Dunbar. “Validation of the normalized difference vegetation index as a measure of neighborhood greenness” en: Ann Epidemiol. Vol. 21, no. 12. EE.UU., National Institutes of Health, 2011, pp. 946-952 (DE) bit.ly/3xZDUrB, consultado el 21 de agosto de 2017.

Roller, N. Remote sensing of wetlands. EE.UU., ERIM, NASA, 1977, 168 p.

Rouse, J., R. Haas, J. Schell and D. Deering. Monitoring Vegetation Systems in the Great Plains with ERTS. EE.UU., Remote Sensing Center, Texas A&M University, College Station, Texas, 1974, pp. 309-317 (DE) go.nasa.gov/3Wqk2qX, consultado el 17 de agosto de 2017.

Schiewe, J. “Segmentation of high-resolution remotely sensed data. Concepts, applications and problems”, en: Symposium on Geospatial Theory Processing and Applications. Ottawa, 2002 (DE) bit.ly/3y6PalZ, consultado el 6 de abril de 2018.

Sorensen, M., V. Barzetti, K. Keipi y J. Williams. Manejo de las áreas verdes urbanas. Documento de buenas prácticas. Washington, DC, BID, 1998, 81 p.

Tilton, J. C., S. Aksoy and Y. Tarabalka. “Image Segmentation Algorithms for Land Categorization”, en: P. S. Thenkabail (ed.). Remote Sensing Handbook. Taylor and Francis, 2015, pp. 317-342 (DE) bit.ly/3Ya9LAh, consultado el 6 de abril de 2018.

Vlahov, D. and S. Galea. “Urbanization, Urbanicity, and Health”, en: Journal of Urban Health: Bulletin of the New York Academy of Medicine. Vol. 79, no. 4, Supplement 1. EE.UU., New York Academy of Medicine, 2002, 12 p. (DE) bit.ly/4f5TwdJ, consultado el 19 de agosto de 2017.

WHO. Urban Green Spaces and Health, A review of evidence. Copenhagen, Denmark, World Health Organization Regional Office for Europe, 2016, 92 p.

Xie, Y., Z. Sha and M. Yu. “Remote sensing imagery in vegetation mapping”, en: Journal of Plant Ecology. Vol. 1., no.1. Reino Unido, Oxford Academic, 2008, pp. 9-23 (DE) bit.ly/3zPiUEv, consultado el 24 de agosto de 2017.

Xie, Y., H. Wang, L. Li y X. Zhao. “The application of threshold methods for image segmentation in oasis vegetation extraction”, en: 18th International Conference on Geoinformatics: GIScience in Change, Geoinformatics, 2010. Pekin University, Beijing, China, June 10-20 (DE) bit.ly/3zQ5hF6, consultado el 6 de abril de 2018.

Xue, J. and B. Su. “Significant remote sensing vegetation indices: a review of development and applications”, en: Journal of Sensors. Vol. 2017. EE.UU., Hindawi, 2017, pp. 1-17 (DE) bit.ly/3W8HJ5M, consultado el 27 de agosto de 2017.

---

¹ Se le denomina así a cada uno de los segmentos en los que se organiza el espectro electromagnético “…en función de su longitud de onda (…) en donde la radiación electromagnética manifiesta un comportamiento similar (…) Comprende (…) desde las longitudes de onda más cortas (rayos gamma, rayos X), hasta las kilométricas (telecomunicaciones)…” (Chuvieco, 1995, p. 48).