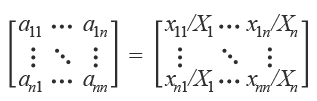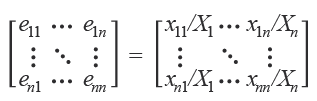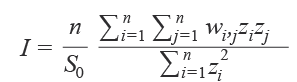Insumo-producto regional: una estimación basada en técnicas de dependencia espacial

 

Regional Input-Output: an Estimate Based on Spatial
Dependency Techniques

José Antonio Huitrón Mendoza
Universidad Nacional Autónoma de México, jose_eco71@comunidad.unam.mx

Vol. 12, Núm. 2  – Epub                                                       Insumo-producto regional… – Epub

 

En este trabajo se presenta un método alternativo para la construcción de matrices de ponderadores de intercambio de insumo-producto en microrregiones, combinando el análisis de una cadena de valor con técnicas de análisis de dependencia espacial e identificación de clústeres, de forma tal que la dependencia espacial indica relaciones sectoriales. Se encontró que, a partir del método propuesto, se identificaron relaciones espacio-sectoriales y fue posible estimar una matriz de relaciones económicas para el caso del sector manufacturero de la Zona Metropolitana del Valle de México. La conclusión principal del estudio consiste en que el método utilizado puede servir como base para el diseño de un sistema de interacción sectorial espacial basado en criterios de validación estadística de las relaciones económicas identificadas. Palabras clave: insumo-producto regional; análisis de dependencia espacial; matrices ponderadas de intercambio.

This work presents an alternative method for the construction of input-output exchange weighting matrices in micro-regions, combining the analysis of value chain with spatial dependence analysis techniques and the identification of clusters. The basic idea is spatial dependency is indicative of sectoral dependency. It was found that, based on the proposed method, spatial-sectoral relationships were identified and it was possible to estimate a matrix of economic relationships for the case of the manufacturing sector of the Metropolitan Zone of the Valley of Mexico. The main conclusion of the study is that the method used can serve as a basis for the design of a spatial sectoral interaction system based on statistical validation criteria of the identified economic relationships. Michigan                                                                Key words: Regional Input-Output; Spatial Dependency Analysis; Weighted Exchange Matrices.

Recibido: 12 de marzo de 2020.
Aceptado: 26 de octubre de 2020.

Introducción

De forma relativamente reciente se han generado estudios de perfil empírico donde se presentan metodologías y técnicas para la construcción de matrices de insumo-producto regional (MIPR); la idea es tener estimaciones de los volúmenes de transacciones o, en general, de la forma de relacionarse de las actividades económicas de un espacio con otros a partir de intercambios económicos entre sectores. Estos instrumentos permiten obtener información para la implementación de medidas de política económica, industrial o solo para conocer la estructura y las formas de complementariedad entre las regiones.

Los métodos que se utilizan para la construcción de MIPR son diversos y responden a las necesidades de investigación o de conocimiento de aspectos particulares de los lugares específicos para los cuales se han realizado ejercicios y estudios.

Este documento tiene como objetivo principal construir una matriz de interacción de insumo-producto aplicado a la industria manufacturera de la Zona Metropolitana del Valle de México (ZMVM), aunque, como veremos, el método podría ser generalizable para conocer y validar estadísticamente la estructura de interacción de espacios asociados a una actividad económica determinada. Para este propósito, se utiliza uno basado en la conciliación de información disponible en la matriz insumo-producto nacional del 2013 y los Censos Económicos 2014;^[1] la idea central es usar técnicas de análisis de dependencia espacial para observar cuáles son las posibles interacciones entre el mismo sector, pero emplazado en lugares distintos.

A partir de la identificación del principal clúster industrial de la ZMVM, podremos establecer las relaciones del sector manufacturero en los municipios y delegaciones^[2] que lo componen; estos lazos se validan a partir de pruebas estadísticas y, de esa manera, se suponen las basadas en intercambios en forma de compras y ventas entre unidades espaciales.

El documento está organizado de la siguiente manera: se hace una breve revisión de la literatura con respecto al análisis insumo-producto regional; después, se expone la metodología utilizada para la construcción de la matriz de relaciones propuesta; posteriormente, se presentan los resultados, así como el análisis y, al final, se ofrece un apartado de conclusiones y discusión.

 

Estudios de insumo-producto regional

El Modelo de Insumo-Producto de Wassily Leontieff (1951), en el que se presenta la estructura de una economía mediante el conocimiento de la producción de cada sector y la forma en la que es consumida por los otros, ha sido un instrumento muy utilizado para diversos fines: científicos, de planeación económica, de decisiones de política industrial, política salarial, impacto ambiental y análisis de comercio, entre muchos.

De acuerdo con Fuentes (2005), para el caso de México se cuenta con matrices de insumo-producto oficiales a nivel nacional desde 1950 y su actualización más reciente fue en el 2013. En ese mismo trabajo se aborda que para la construcción de matrices a escala regional hay métodos como el full survey, que consiste en el levantamiento de grandes volúmenes de información para poder conciliar y establecer la forma en la que los sectores ubicados en áreas geográficas específicas se relacionan entre sí; sin embargo, este en particular implica costos muy elevados, por ello, no es usual que se ponga en práctica.

Existen, desde luego, otras vías para llevar a cabo la estimación de matrices de interacción sectorial regionales o MIPR: las que utilizan encuestas a partir de muestras y, con ello, indagan las relaciones entre regiones específicas y entre sus sectores, y como la que aplicaremos en esta propuesta, basada en el concilio de información de las fuentes disponibles. En nuestro caso, hacemos uso de dos instrumentos principales: la matriz insumo-producto nacional de 20 sectores del 2013 y los Censos Económicos 2014.^[3]

Por medio del análisis insumo-producto es factible la identificación de clústeres, o complejos industriales, que se definen como concentraciones de industrias que, además, presentan una tendencia a localizarse con cercanía geográfico-espacial y, por supuesto, vinculadas por un intenso intercambio de bienes y servicios (Domínguez y Valle, 1999).

Miller y Blair (2009) tienen un trabajo que se ha convertido en un referente obligado para los estudios de insumo-producto contemporáneos en el que exponen la forma en como se han hecho propuestas de aproximación a las matrices regionales, reconociendo el hecho de que, a la fecha, la mayoría de los modelos consideran procedimientos consistentes en la adaptación de los coeficientes de las matrices nacionales a determinadas escalas subnacionales, como estados, conjuntos de estos o centros metropolitanos, haciendo uso de indicadores económicos que permitan ponderar la participación de esas regiones específicas, pero sin que ello implique necesariamente que las estimaciones sean fieles a la estructura tecnológica y de requerimientos de insumos de estas. Un punto de coincidencia con la propia presentación de Miller y Blair (2009, p. 70) es que se ha hecho en una cantidad importante de trabajos al respecto sobre el insumo-producto regional, los cuales están consignados en publicaciones como Economic Systems Research, Journal of Regional Science, International Regional Science Review y Papers in Regional Science; muestra de esta amplia gama de trabajos están, por ejemplo, los de Hewings y Jensen (1987), Rose y Allison (1989), Oosterhaven (1989), Jensen (1980), Lenzen et al. (2017), Peters et al. (2011) y Andrew et al. (2009). Lo que se muestra al explorar estas investigaciones es el desarrollo de una amplia gama de metodologías con algunos puntos en coincidencia, donde la tarea fundamental recae en establecer formas de regionalizar los coeficientes de las matrices nacionales y adaptarlos a estructuras regionales que, se reconoce, son diversas en estructura y capacidades tecnológicas, así como las relaciones que puedan establecerse entre las actividades económicas y el espacio.

Lo anterior hace referencia explícita a la agenda de investigación sobre las matrices regionales (desde el punto de vista de Schuschny, 2005). A este nivel, los métodos de identificación de concentraciones y relaciones entre las mismas tienen aún un carácter cualitativo, aspecto con el cual en este trabajo estamos en acuerdo, pues la principal limitación es que no hay datos estadísticamente consistentes para construir matrices regionales que sean compatibles con la información agregada a nivel nacional.

Hay diversos estudios aplicados para el análisis de insumo-producto regional en México, por ejemplo, el de Asuad (2019), donde se propone un método basado en la construcción de cuentas estatales de producción conciliando información desde abajo, partiendo de diversas fuentes de datos, donde se busca reexpresar los que faltan con un método de regionalización indirecta con base en los datos nacionales y suponiendo la relación entre las actividades económicas/espacios mediante coeficientes de especialización económica; la forma de estimar los intercambios es sencilla: los espacios especializados en una determinada actividad son exportadores, mientras que los no especializados tienden a importar.

Puede identificarse otra serie de trabajos, como el de Chiquiar et al. (2017), que utilizan el Método de Flegg para estimar cuatro matrices correspondientes con la regionalización del Banco de México; el de Torre et al. (2017), donde evalúan los impactos regionales de la construcción de una planta automotriz, así como los efectos de la propia producción de esta, haciendo uso de la regionalización del Banco de México y la técnica de Flegg. Más allá de que este método tenga un alcance importante, dado que es muy utilizado para regionalizar matrices, lo que en realidad significa en el análisis es reescalar las matrices nacionales, pero sin que ello signifique capturar la heterogeneidad de las regiones en las cuales se aplica; es decir, se asume que, por ejemplo, una entidad federativa tendría exactamente la misma estructura productiva y tecnológica en comparación con la escala nacional, aspecto que puede identificarse como una debilidad metodológica, pues no se están considerando elementos de carácter estructural a escalas menores de análisis geográfico.

Hurtado y Martínez (2017), a partir de un método de redes binarias, presentan un ejercicio para la economía de Medellín en Colombia, identificando encadenamientos hacia atrás y hacia adelante, considerando diversas relaciones intersectoriales e intrasectoriales.

Hay varios trabajos desarrollados para regiones o estados en México, como el de Albornoz, Canto y Becerril (2012), donde evalúan las interrelaciones productivas de la economía de Yucatán; también se encuentran antecedentes como el de Callicó, Bouchain et al. (2000) que aborda, a nivel teórico y algunas aplicaciones, el insumo-producto regional para casos de México; o el de Fuentes, Lugo y Herrera (2004), donde trata el cálculo de una matriz de insumo-producto para Baja California. En general, todos los métodos enunciados tienen en común una limitación importante ya abordada por Mariña (1993): suponer que la estructura tecnológica y de costos de los sectores ubicados en cada lugar específico es similar a la nacional; a esto se suma la problemática de que no se ha sistematizado con un método estadístico consistente la manera en la cual los distintos espacios productivos interactúan.

En general, en los estudios mencionados se identifica que los enfoques son diversos y que hay una variedad de técnicas desde las cuales es posible abordar la construcción de matrices de insumo-producto regional. Vale la pena revisar el trabajo reciente de Oosterhaven (2019). Nuestra conclusión al respecto es que las técnicas de regionalización que parten de la noción de intercambios sectoriales dependen del objetivo de cada investigación; el reto fundamental es establecer un método coherente para trasladar la información que surge de las matrices calculadas a nivel macroeconómico a los aspectos regionales o, incluso, al de microrregión.

 

Metodología

Para la construcción de nuestro ejercicio básico de insumo-producto regional, se plantea una ruta metodológica consistente en dos etapas: la primera es identificar la cadena de valor asociada al sector manufacturero haciendo uso de la matriz simétrica de insumo-producto del 2013, que expresa las relaciones industria por industria; la segunda es calcular por medio del análisis de un sistema de información geográfica (SIG) las regiones funcionales hipotéticas que se generan en términos de los eslabonamientos más fuertes encontrados en la cadena de valor, esto servirá para esquematizar la manera en la que se dan las relaciones entre los lugares en los cuales se encuentran presentes los sectores relacionados entre sí, de tal suerte que podemos catalogar nuestro método de análisis de tipo de arriba hacia abajo (top-down).

La forma en la que se utilizará el SIG es mediante un análisis de dependencia espacial; el supuesto es que serán las unidades espaciales que forman clústeres las que puedan considerarse como regionalmente funcionales si se comprueba la hipótesis de que existe una relación entre la producción de las unidades espaciales; ello quiere decir que, efectivamente, la producción en un lugar depende o presenta algún tipo de interrelación con la que se desarrolla en otro espacio geográfico.

Para llevar a cabo este planteamiento, primero se hará el cálculo de los coeficientes de demanda y de oferta, poniendo especial atención en la cadena empírica correspondiente al sector 31-33 de la industria manufacturera; este paso es de particular importancia, pues permitirá evaluar el grado de pertinencia de tener cálculos de insumo-producto regionales, en el entendido de que actualmente las relaciones sectoriales se explican en un contexto donde las cadenas de valor tienen una integración internacional; por ejemplo, para el caso de la industria automotriz mexicana —que para el 2016 representó 3.3 % del Producto Interno Bruto (PIB) nacional y 19.6 % del PIB manufacturero mexicano— se estima que el componente importado es de alrededor de 54 %, todo con base en datos de PROMÉXICO (2016); es decir, gran parte de las relaciones de las actividades económicas más importantes que se realizan en el país están estrechamente relacionadas con espacios ubicados fuera de sus fronteras. Siguiendo a Mariña (1993), los coeficientes de interdependencia de demanda se estiman dividiendo cada elemento de la matriz de transacciones intersectoriales (x_ij) entre el total de su respectiva columna, integrando como un vector fila a las importaciones; así, cada componente (a_ij) muestra la cantidad de insumos nacionales e importados i para producir una unidad de producto j, en términos de un porcentaje; matricialmente, la expresión es:

(1)

Por el lado de la oferta, la operación consiste en dividir cada elemento de la matriz de transacciones intersectoriales (x_ij), incluido un vector columna de exportaciones, entre el total de su respectivo renglón; cada uno de sus componentes (e_ij) registra la parte de cada unidad de oferta del sector i que se utiliza como insumo en el sector j; matricialmente, esto se expresa como:

(2)

 

Lo anterior tiene una implicación metodológica en referencia con los cálculos de matrices a escala subnacional; es preciso investigar, previo a los cálculos de relaciones sectoriales regionales, el componente importado de las industrias o sectores económicos que se desee analizar. La justificación de esto es evitar hacer una sobrerrepresentación de las relaciones encontradas, en el entendido de que es aún más complejo investigar la forma en la que un sector industrial ubicado en un estado específico se relaciona con otros lugares y sectores fuera del país o en otros estados o cualquier otro nivel de desagregación geográfica para la cual se disponga de información.

A partir de la construcción matricial de las expresiones (1) y (2) se propone la elaboración de la cadena de valor empírica y contar, así, con una medición previa a las consideraciones de tipo local; además, el objetivo con esta primera parte del ejercicio es indagar, para este sector en particular, cuáles son sus relaciones sectoriales más relevantes en términos de compras de insumos, incluidas las importaciones y ventas, considerando las exportaciones.

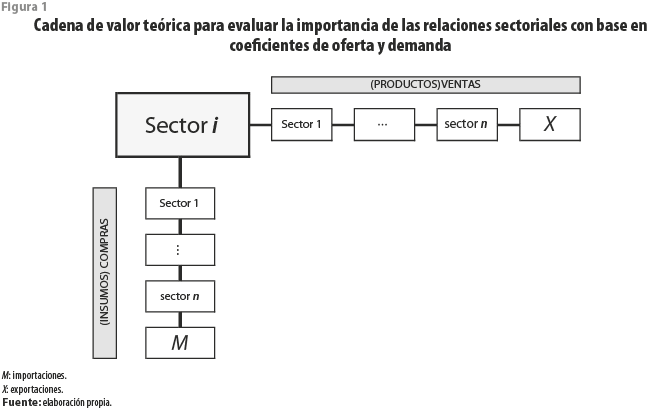
La figura 1 presenta la forma de una cadena de valor empírica que deriva de las expresiones (1) y (2), donde se considera un sector (i) como núcleo de análisis que, en realidad, está ubicado en un espacio específico y tiene relación con otros sectores-espacios, hacia atrás en términos de compras o insumos y hacia adelante en términos de ventas o productos. Para el presente ejercicio, nos limitaremos a considerar que una región es económicamente funcional^[4] con respecto a otra si comparten ese tipo de encadenamientos sectoriales y esto se asocia a la presencia de indicios estadísticos del  intercambio de insumos y productos.

Una vez construida la cadena de valor empírica (de la industria manufacturera, en este caso) y habiendo identificado cuáles son los sectores con los que se relaciona en ambos sentidos (compras y ventas), a partir del uso de un SIG se hará la identificación de clústeres por medio del cálculo del Índice de Moran Local, el cual es un método para la evaluación de dependencia espacial que se valida estadísticamente aplicando una simulación de Montecarlo.

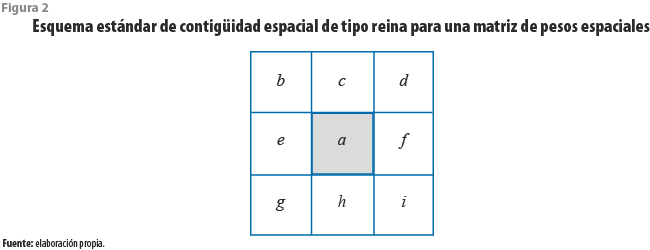
La idea de este índice es identificar si existe relación estadística entre los datos que se generan en una unidad espacial y las unidades vecinas; por ejemplo, tomando en cuenta la unidad a de la figura 2, al evaluar la dependencia espacial, se diría que lo que ocurre ahí es producto de efectos de interacción (en este caso, económica) con b, c, d, e, f, g, h e i, de tal forma que si, por ejemplo, lo que se está evaluando es que la producción manufacturera de a guarda relación estadística con la de sus vecinos, entonces hay evidencia que sustenta una estructura de interacción sectorial-espacial entre esas unidades de análisis geográfico. En un vecindario de forma cuadrada se puede definir un conjunto de unidades espaciales de análisis como (x₀, y₀) donde el rango de vecindad u orden de una matriz de pesos espaciales se define formalmente así:

 (3)

donde  expresa un vecindario de tipo Moore.^[5]

Los vecindarios dependen del valor que asume r; por ejemplo, si es 1, se trata de uno de orden 1, es decir, son contiguas o guardan relación en términos espaciales las unidades que comparten una arista o un vértice con una unidad específica, con órdenes superiores; la lectura es que, además de los vecinos inmediatos, también se incluiría en las estimaciones la relación espacial con los de en segundo o tercer orden y así sucesivamente; aunque, como veremos, esto genera que, a mayores órdenes de vecindad, los cálculos implican una disminución de importancia estadística de las mediciones. Para este trabajo, el supuesto es que dichas relaciones de dependencia pueden significar encadenamientos productivos entre las unidades espaciales de análisis y, en ese sentido, considerar a una delegación o municipio como espacio económicamente funcional con respecto a otros.

En la figura 2 suponemos, además, que en la construcción del Índice de Correlación Espacial de Moran, lo que sucede en una unidad de análisis está mayormente determinado por las unidades cercanas y que los efectos de dependencia son menores en cuanto más lejanas están; para este caso específico, estamos probando matrices de contigüidad de primer orden, es decir, serán consideradas vecinas de una unidad espacial aquellas que comparten una arista o un vértice desde el punto de vista geométrico, aunque de hecho se ha demostrado que esto es un camino para evaluar efectos de proximidad en los fenómenos económicos y, en general, de corte social.

La autocorrelación espacial de Moran mide el grado de asociación espacial de los datos para un conjunto de ellos; lo que se evalúa es si hay una tendencia a la agrupación, dispersión o si existe una distribución puramente aleatoria. La expresión matemática del índice se construye de la siguiente manera:

(4)

donde:

z_i = desviación de una variable de la unidad i de su media .

w_i,j = matriz de pesos espaciales o de relaciones entre las unidades i y j.

n = número de unidades de análisis.

S₀ = sumatoria de los pesos espaciales consignados en la matriz w_i,j.

En sentido estricto, la fórmula matemática del índice proviene de la noción del coeficiente de correlación de Pearson, pero incluye la matriz de pesos espaciales que pondera la relación de la información perteneciente a una unidad espacial con el conjunto de sus unidades vecinas; para profundizar en este aspecto, se sugiere consultar el texto de Anselin (2005, pp. 106-123).

Para validar el Índice de Moran, se realiza una simulación de Montecarlo que consiste en poner, mediante un algoritmo de cómputo, los valores de cada uno de los espacios de manera aleatoria con el fin de contrastar un número de adjudicaciones posibles con la asignación empírica de los datos; si esto no es coincidente se puede concluir que, efectivamente, los datos empíricos no son producto de una asignación casuística, sino de procesos de interacción que apelan a la estructura económico-geográfica evaluada. Además, se obtiene un pseudo valor p, un z, un Índice de Moran estimado empíricamente y otro simulado; todos estos parámetros en conjunto ayudan a tener criterios estadísticos sobre si los patrones de asociación de los datos en el espacio son en realidad significativos.

Si se identificara una concentración de información para un determinado sector de estudio y que esta fuera significativa de forma estadística, estaríamos en la posibilidad de afirmar que la producción de un lugar determinado depende espacialmente de lo que ocurre en su contexto inmediato cercano; así, al aplicar el método a los datos de la manufactura de la ZMVM, podríamos sostener que, en esos municipios o delegaciones donde sea válida de manera estadística la agrupación, existen relaciones bidireccionales y son entre sí regiones económicamente funcionales en términos de intercambio de bienes o servicios.

La otra idea que se refuerza es que en esas agrupaciones de espacios funcionales encontradas es donde se llevan a cabo las interrelaciones económicas entre los sectores identificados, esto mediante la guía que surge del análisis de la cadena de valor en el análisis insumo-producto macroeconómico.

Una vez obtenidas las relaciones de la industria manufacturera hacia atrás y hacia adelante, en este trabajo se evaluarán las que existen con respecto al eslabonamiento más fuerte hacia adelante y hacia atrás en términos de la economía interna y se determinarán las de intercambio entre regiones funcionales (municipios y delegaciones) de la ZMVM utilizando la identificación de clústeres por medio del Índice de Correlación Espacial de Moran.

Con base en estos resultados se construirá una matriz de interacción espacial señalando el tipo de relaciones (unidireccionales o bidireccionales) a partir de la clasificación de las unidades espaciales de análisis conforme al lugar que ocupan en la geografía de la ciudad; es decir, si forman parte de una agrupación de unidades dentro de un clúster o fuera de este, además de señalar el peso hipotético de las transacciones entre dichos lugares.

En el cuadro 1 se consigna, a modo de síntesis, el método propuesto para la construcción de la matriz de intercambios en las regiones económico-funcionales determinadas mediante el análisis de dependencia espacial.

 

Resultados

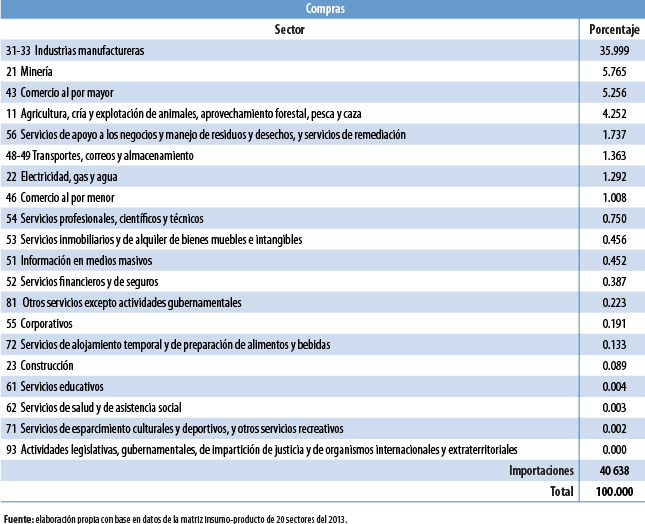
A partir de datos de la matriz simétrica insumo-producto nacional total del 2013 a nivel sector, se calculó la cadena de valor empírica asociada con el sector manufacturero por medio de la obtención de los coeficientes de interdependencia total;^[6] se encontró que existe una fuerte relación hacia atrás con respecto al mismo sector: 35.9 % de las compras que realiza las hace a sí mismo. El dato que más llama la atención es que, en promedio, una empresa manufacturera importa alrededor de 40.6 % de los bienes que utiliza para producir; el hecho de que el componente importado sea tan alto implica que, en términos de la construcción de un análisis insumo-producto regional (que solo considera las interacciones entre empresas o industrias residentes), los eslabonamientos identificables por sector-región tienden a ser muy bajos cuando los coeficientes importados que se registran son altos.

Lo anterior implica una reflexión sobre el papel de la actividad industrial como posible pauta de desarrollo; en presencia de altos coeficientes de importaciones sería una limitación importante, pues habría indicios, en este nivel de análisis, de que cuando crece la producción manufacturera en las regiones mexicanas, los efectos de arrastre no se dan solo al interior de la economía, sino que también hay efectos fuera de las fronteras; este punto, incluso, limitaría el alcance de los instrumentos regionales de insumo-producto como mecanismo de elaboración de política industrial o, en general, de la económica.

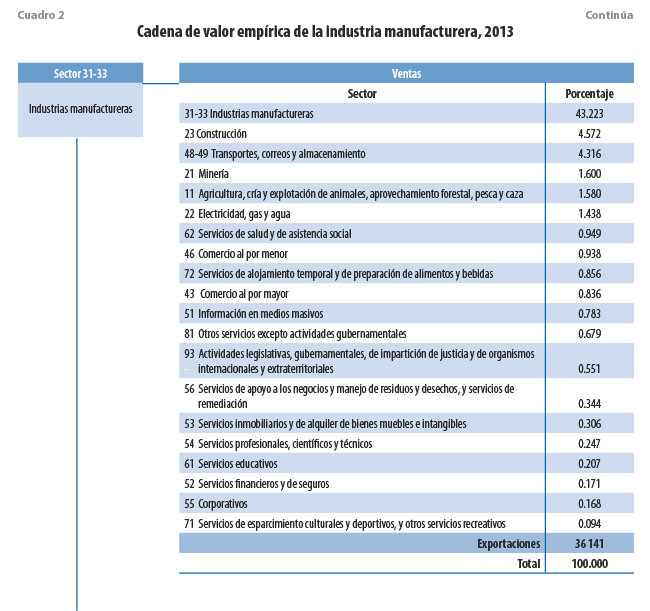
Asimismo, para este nivel de desagregación de la matriz de insumo-producto, se encuentra que las industrias manufactureras guardan una relación relativamente importante con otras en términos de compras necesarias para producir, como es el caso de la minería (5.76 %); el comercio al por mayor (5.26 %); la agricultura (4.25 %); los servicios de apoyo a los negocios (1.73 %); transportes, correos y almacenamiento (1.36 %); electricidad, gas y agua (1.29 %); y el comercio al por menor (1 %); el resto de los sectores representan, en términos de compras, 2.68 por ciento. En realidad, se puede concluir parcialmente que este sector guarda una alta interdependencia económica consigo mismo y con el exterior; por ello, se entiende como un sector de transformación en referencia a sus relaciones con los demás que están dentro de la economía. Por otro lado, prevalece una implicación importante en la funcionalidad de esta actividad; se podría afirmar que esta es altamente dependiente de la dinámica económica externa.

Por el lado de las ventas, las dos principales interdependencias son: la propia industria manufacturera con 43.22 % de las ventas y las exportaciones que representan 36.14 %; esto permite reforzar una idea en el análisis: la industria manufacturera en México y, por ende, en las regiones donde está presente, tienen relaciones fuertes y con un grado alto de consolidación hacia el exterior desde la perspectiva de las importaciones necesarias para generar bienes y servicios; por otro lado, el destino de esa producción (los mercados externos) son un motor determinante de la demanda; ver, por ejemplo, los trabajos de Fuji (2000) y Almagro (2011).

Los otros sectores con los que existe un eslabonamiento relativamente importante —aunque podría caracterizarse como bajo hacia adelante (ventas)— de la industria manufacturera son: la construcción (al que se destina 4.57 % de las ventas); transportes, correos y almacenamiento (4.31 %); minería (1.6 %); agricultura (1.58 %); y electricidad, gas y agua (1.43 %); al resto se les vende 7.13 %, en conjunto.

Más allá de la información que se ha obtenido de la cadena de valor lograda a partir de los datos de los coeficientes de interdependencia analizados (ver cuadro 2), las cifras sirven para perfilar la siguiente parte del análisis, la cual consiste en identificar los municipios o delegaciones que son económicamente funcionales en la ZMVM. Como hemos identificado que las principales relaciones se dan con el mismo sector a este nivel de agregación de la información, es pertinente indagar cuáles son los lugares que tienen una jerarquía mayor en la producción manufacturera, de tal suerte que ello permita establecer relaciones entre esos espacios-sectores.

Con base en lo anterior, podríamos también explorar, por ejemplo, la conexión que hay entre la industria manufacturera de la ZMVM con el sector agrícola (o cualquier otro), ubicado en la propia área de estudio, replicando el ejercicio propuesto y, así, saber cómo, en función de la relación sectorial que deseemos investigar, es que se configuran las de insumo-producto que se presenten en distintas configuraciones espaciales; es probable que la relación espacial del sector industrial en la ZMVM sea entre un núcleo localizado en la zona central (donde está localizada la industria manufacturera) y las periféricas, donde es sabido que aún hay municipios que guardan algo de vocación productiva inclinada al sector primario.

 

El supuesto principal sobre la medición a partir de la identificación de concentraciones de la industria manufacturera es que aquellos lugares donde se encuentren clústeres consolidados (evaluados estadísticamente) son los que cumplirán tres características: 1) está presente la industria manufacturera; 2) comparten relaciones de tipo insumo-producto fuertes y 3) por el punto anterior, pueden ser consideradas regiones económicamente funcionales.

Para la identificación de las concentraciones de unidades espaciales, se construyó una matriz de pesos espaciales tipo reina (equivalente al vecindario tipo Moore) de primer orden;^[7] esto significa que, para la identificación del clúster más importante de manufactura en la ZMVM, se atiende a la noción de la primera ley de la geografía, o principio de autocorrelación espacial, de Tobler (1969), la cual sostiene que: “Todas las cosas están relacionadas entre sí, pero las cosas más próximas en el espacio tienen una relación mayor que las distantes.”; así, podemos argumentar que para evaluar los posibles encadenamientos productivos regionales o microrregionales entre unidades económicamente funcionales serán más fuertes las relaciones sectoriales cuando la producción de determinadas regiones sea cercana geográficamente y, además, estas unidades de análisis compartan una característica fundamental: tener una alta concentración de producción manufacturera y, a su vez, estar rodeadas de unidades que cumplen esa misma condición.

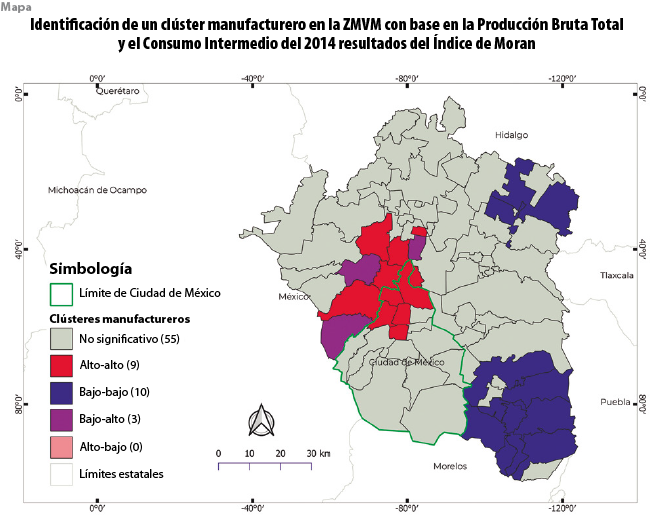
En el mapa se identifica en la zona central una concentración de unidades espaciales que tienen como característica principal un valor alto de Consumo Intermedio, rodeadas de otras con altos valores de Producción Bruta Total (municipios y delegaciones en rojo); de acuerdo con la metodología propuesta, son estos lugares los que presentan un grado mayor de interacción en la lógica insumo-producto, ello sustentado en la noción de que serán más fuertes las relaciones sectoriales entre espacios que cuenten, para este caso, con una presencia consolidada de actividades manufactureras en términos de la utilización de insumos y donde es alta la probabilidad que el producto bruto de las unidades vecinas sea el sustento material de los mismos.

Se identifica, también, que el sector manufacturero en la ZMVM se expresa en un emplazamiento de tipo centro-periferia; es decir, un núcleo de tipo central con una gran relevancia y donde las zonas periféricas tienen una presencia significativamente menor del sector objeto de estudio, al estilo de los modelos gravitacionales, como los presentados en los trabajos de Haddad y Azzoni (2003), Boero, Edwards y Rivera (2017) y de Marto (2009, 153-160); en este último se hace una presentación exclusivamente teórica.

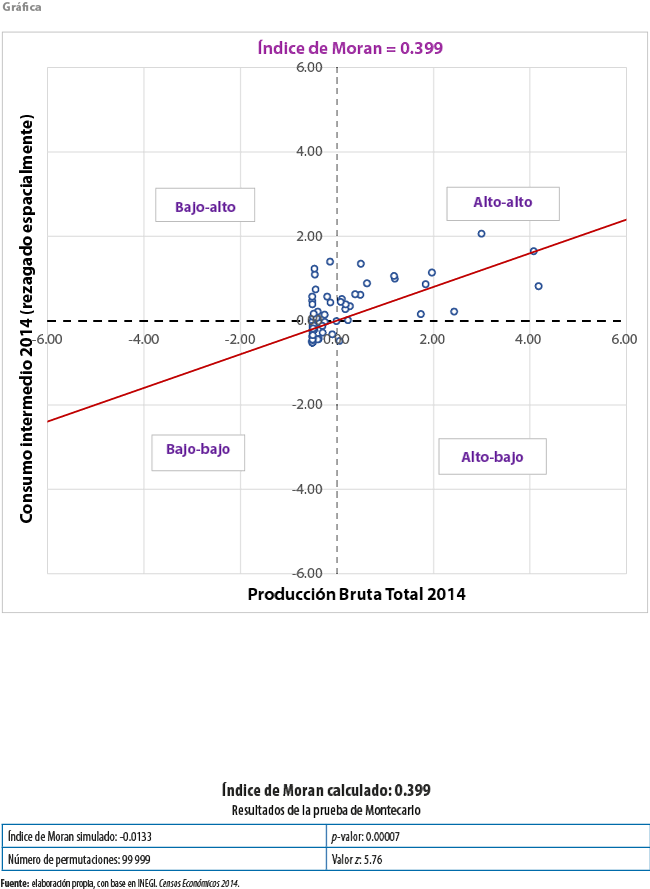
En la gráfica se muestran las concentraciones identificadas mediante el cálculo del Índice de Moran Bivariado aplicado mediante la técnica de identificación de indicadores locales de asociación espacial.^[8] Los resultados de la estimación muestran que los clústeres son estadísticamente significativos, en razón de que el Índice de Moran calculado y el simulado se encuentran lejanos, el p-valor es cercano a cero y el valor z está alejado del valor crítico 1.96; por todo lo anterior, puede rechazarse la hipótesis nula de no dependencia espacial y, en contraste, reforzar la idea de que en las unidades identificadas hay un tipo de correlación entre los datos espaciales que está basada en la estructura económico-geográfica de la zona de estudio y no es producto de efectos puramente aleatorios.

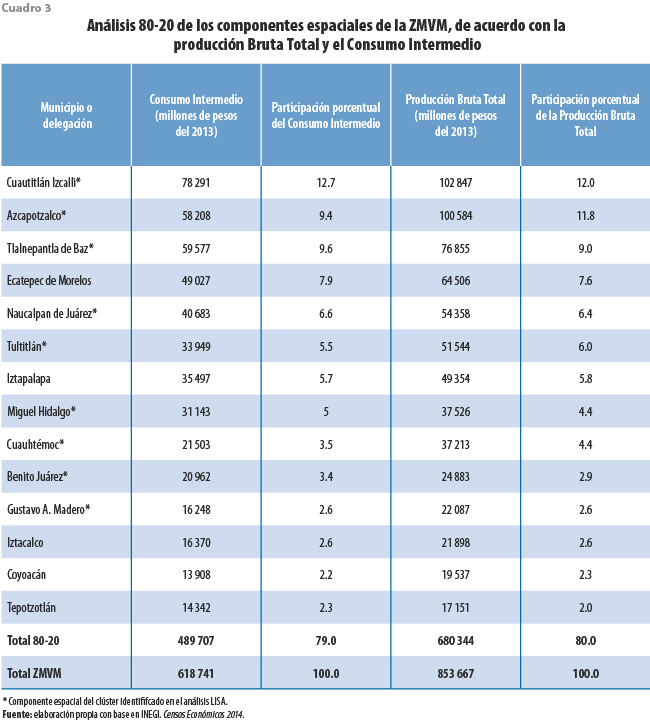
En el cuadro 3 se muestra el peso relativo de los principales componentes espaciales de la ZMVM de acuerdo con el sector manufacturero. Con el objetivo de reforzar la idea de la relevancia del núcleo identificado, se presenta en un análisis 80-20 a modo de comprobar que, efectivamente, las unidades espaciales que componen dicho núcleo forman parte del clúster identificado en el análisis bivariado LISA y participan por sí mismas en 59 % de la producción bruta manufacturera; esto refuerza la idea de que la mayor parte de las interacciones del sector manufacturero se dan entre sí y en esos lugares.

La información encontrada a partir del ejercicio indica que es en esta agrupación de unidades delegacionales y municipales donde se establecen las relaciones económicas funcionales y los intercambios de tipo insumo-producto más importantes de la ciudad, lo cual da pie a indagar la magnitud de las relaciones sectoriales entre esas unidades de análisis. En este ejercicio se estimarán las relaciones entre la propia industria manufacturera, hacia atrás y hacia adelante, en los componentes del clúster identificado.

 

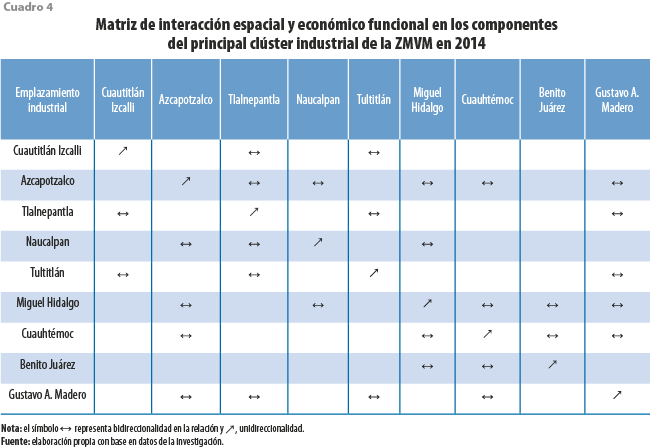
En el cuadro 4 se presenta la forma en la que las unidades espaciales de análisis interactúan de acuerdo con el clúster industrial identificado; como se mencionó arriba, la matriz de pesos espaciales utilizada para el análisis LISA es una de tipo reina de primer orden. La lectura que debe darse, por ejemplo, para el caso de la delegación Azcapotzalco, es que esta tiene una relación económicamente funcional fuerte tanto con los municipios de Tlalnepantla y Naucalpan como con las delegaciones Miguel Hidalgo, Cuauhtémoc y Gustavo A. Madero y ellas, a su vez, con Azcapotzalco; debido a que estas unidades están en el entorno inmediato, para el caso de la diagonal principal la idea es que si las empresas manufactureras ubicadas en una unidad de análisis hacen intercambios entre sí, la relación sería circular (en forma de loop).

El supuesto para construir finalmente la matriz de ponderadores de intercambios de tipo insumo-producto para esta subregión de la ZMVM identificada es que, dependiendo del peso relativo que tenga cada unidad de acuerdo con la Producción Bruta Total o el Consumo Intermedio y con base en los eslabonamientos identificados a partir del análisis macroeconómico, es posible ponderar las transacciones que teóricamente se dan entre estas unidades, en específico entre la industria manufacturera de cada unidad de análisis con respecto a las otras.

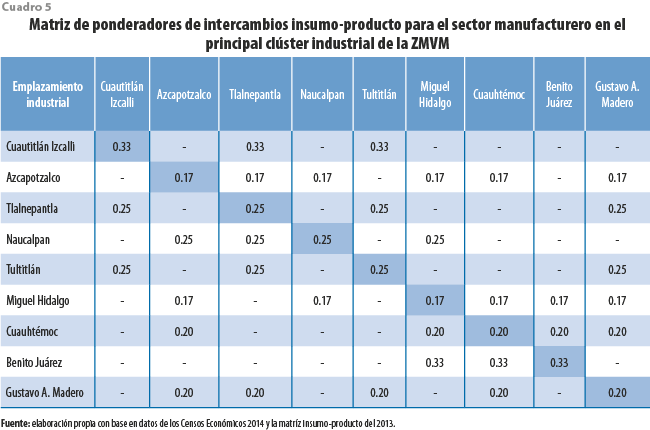
En el cuadro 5 se muestran las estimaciones de los ponderadores de intercambio insumo-producto para los municipios y delegaciones del principal clúster industrial de la ZMVM; la lectura correspondería con el siguiente razonamiento: para el municipio de Cuautitlán Izcalli, su industria manufacturera estaría adquiriendo 33 % de los insumos de las propias empresas manufactureras ubicadas ahí y los dos tercios restantes de la de Tlalnepantla y Tultitlán; este mismo resultado se aplica para el caso de las ventas, pues de acuerdo con la propuesta metodológica es con las unidades ubicadas en el contexto inmediato con las que es más fuerte la relación económica; si bien la medición puede parecer restrictiva, da una vívida idea de cómo se llevan a cabo esos intercambios, porque en realidad cada municipio tiene relación con lugares más lejanos, incluso fuera del país; sin embargo, para áreas pequeñas, estas estimaciones permiten tener una estructura analítica de estos a nivel local.

Así, contamos con un método para tener una idea de las relaciones que se dan en el sector manufacturero de un municipio o delegación con la industria de las regiones vecinas y la dimensión de las mismas entre las empresas ubicadas en una misma delegación o municipio. Además, el método puede ser generalizable para cualquier sector de interés analítico.

Si bien los resultados de ninguna forma pueden catalogarse como exactos, aportan una ruta metodológica sobre cómo es posible entender la interacción económica entre regiones con características económicas similares y pone de manifiesto la necesidad de tener información más detallada que permita establecer relacionamientos entre las distintas unidades económicas o sectores, de lugares específicos.

El hecho de que para esta propuesta se considere solo a las unidades cercanas como aquellas con las que se establecen relaciones de intercambio, no limita la posibilidad de hacer otro tipo de ejercicios en los que haya planteamientos diferentes de interacción, por ejemplo, considerar estructuras de vecindario de segundo orden y matrices de distancias, entre otras; los criterios a utilizar pueden ser diversos y dependen del interés de investigación.

Por otro lado, el método también sirve para evaluar las relaciones que pueden existir entre otras actividades económicas y los espacios; por ejemplo, saber si una industria x de un espacio i tiene relaciones significativas (en términos del análisis clúster) con las industrias y de entidades j. Esto, a partir de un análisis del Índice de Moran Local Bivariado, las posibilidades de hecho pueden ser mucho más amplias. En este sentido, el método planteado cuenta con un grado alto de flexibilidad.

 

Conclusiones

El método de estimación propuesto dio como principales resultados la posibilidad de tener un mecanismo de determinación de regiones económicamente funcionales desde el punto de vista de que su interacción es validada de forma estadística.

Existen diversos métodos para el cálculo de relaciones sectoriales a nivel regional; en este caso, propusimos una ruta alternativa echando mano de la estimación de la cadena de valor de un sector en específico; observando las relaciones de ese sector hacia atrás y hacia adelante se eligió el que tenía el peso más relevante en ambos sentidos; después, con el uso de datos de los Censos Económicos 2014 para los municipios y delegaciones de la ZMVM se evaluaron las relaciones de interacción espacial entre estas unidades de análisis con arreglo a la Producción Bruta Total del sector manufacturero identificándose, así, un clúster de lo que denominamos unidades económicamente funcionales. Por último, con base en los pesos relativos de producción de esos municipios o delegaciones y cruzando con la información de la cadena de valor estimada mediante el uso de la matriz insumo-producto del 2013, se pudo construir una matriz de relaciones espaciales-sectoriales en el clúster de manufactura más importante de la ZMVM.

La construcción previa de una cadena de valor permitió identificar que, al menos para el caso de la industria manufacturera a nivel nacional, se tiene un componente importado de 40 %; esto implicó tener ciertas reservas para el planteamiento del propio análisis de insumo-producto regional. Cuando un sector tiene esos niveles de eslabonamiento hacia el exterior, hay de suyo una condición limitante para estimar el propio grado de interacción regional de los sectores.

Se encontró que, a partir de la aplicación de técnicas de análisis de asociación espacial de los datos, se cuenta con un fundamento estadístico sobre la funcionalidad económica de los espacios; asimismo, que es posible establecer una estimación de los intercambios promedio entre los componentes del área de estudio.

Con base en la noción de las matrices de pesos espaciales, se cuenta con una estructura de las posibles interacciones entre los municipios y delegaciones analizados, de tal suerte que se pudo plantear la direccionalidad de las relaciones económicas y, por último, llegar a estimaciones o pesos relativos de las transacciones que se dan entre las unidades de análisis; así, habrá un mayor grado de interacciones cuando los municipios y delegaciones compartan fronteras administrativas con un número mayor de vecinos. Aunque esto es una forma relativamente robusta de acercarse a la problemática, por supuesto es susceptible de mejorarse y discutirse en relación con sus alcances.

Si bien hay métodos ya desarrollados para la construcción de matrices de insumo-producto regionales, todos comparten una limitación en común: la falta de información sobre las interacciones entre las empresas que se ubican en determinadas áreas geográficas con otras. Desde esta perspectiva, algunos métodos tienen más restricciones o supuestos sobre la medición que otros, pero en lo fundamental todos comparten tener el carácter de ser aproximados y con fuertes componentes de índole cualitativa.

Una conclusión sobre este trabajo (y habiendo observado resultados similares) es la probabilidad de que no exista un mecanismo fuertemente confiable para construir matrices de insumo-producto regionales, justo por la existencia de una serie de brechas en la información; en este sentido, los datos que hemos estimado deben asumirse bajo las siguientes condiciones: 1) son cifras aproximadas y 2) se evaluaron interacciones entre unidades administrativas que después consideramos regiones económico-funcionales cuando, en realidad, las interacciones se dan entre empresas; observamos que esta última limitación se da en los demás métodos existentes para la valoración de interacciones sectorial-regionales.

Para finalizar, decimos que partimos de un análisis de tipo arriba hacia abajo (top-down) porque, al no haber información de tipo microeconómica disponible, no es posible establecer cómo, desde espacios pequeños, pueden darse relaciones entre industrias localizadas. Esta es, sin duda, una de las grandes tareas a resolver en el conocimiento de la forma en la que las regiones se complementan, al menos en el ámbito de sus relaciones intersectoriales regionales.

Referencias

Albornoz, L., R. Canto y J. Becerril. “La estructura de las interrelaciones productivas de la economía del estado de Yucatán: un enfoque insumo-producto”, en: Región y Sociedad. Vol. 24, núm. 54. 2012, pp. 135-174.

Almagro, F. “Vulnerabilidad del sector externo de México”, en: Economía y Sociedad. Núm. 28, julio-diciembre. 2011, pp. 63-77.

Andrew, R., G. P. Peters y J. Lennox. Approximation and regional aggregation in multi-regional input-output analysis for national carbon footprint accounting”, en: Economic Systems Research. Vol. 21, núm. 3, 2009, pp. 311-335.

Anselin, L. Exploring Spatial Data with GeoDa: A Workbook. Illinois, Spatial Laboratory Analysis, 2005 (DE)  https://bit.ly/3yKxHdb Fecha de consulta: 20/01/2020.

_______ “Local indicators of Spatial Association”, en: Geographical Analysis. Vol. 27, núm. 2. 1995, pp.93-115.

Asuad, N. Insumo-producto regional: teoría, metodología, técnicas y estudios de caso. México, UNAM-Facultad de Economía, 2019.

Boero, R., B. Edwards y M. Rivera. “Regional input-output tables and trade flows: an integrated and interregional non-survey approach”, en: Regional Studies. Vol. 52, núm. 2. 2017, pp. 225-238.  

Callicó, J., R. Bouchain et al. Insumo-producto regional y otras aplicaciones. México, UAM-A/UNAM/Universidad de Guadalajara, 2003, 454 p.

Chiquiar, D., J. Alvarado, M. Quiroga y L. Torre. “Regional Input-Output Matrices, an Application to Manufacturing Exports in Mexico”, en: Banco de México. Documentos de investigación. Núm. 2017-09. 2017.

Domínguez, H. y J. Valle. Articulación interna de la economía vasca en el periodo 1990-1995. EUSTA, 1999 (DE)  https://bit.ly/3sQV9nV

Fuentes, N. “Construcción de una matriz regional de insumo-producto”, en: Problemas del Desarrollo. Vol. 36, núm. 140. 2005, pp. 89-112.

Fuentes, N., M. Lugo y M. Herrera. Matriz de insumo producto para Baja California: un enfoque hibrido. México, Miguel Ángel Porrúa, 2004.

Fuji, G. “El comercio exterior manufacturero y los límites al crecimiento económico”, en: Comercio Exterior. Noviembre. 2000, pp. 1008-1014.

Haddad, E. y Azzoni. “Localización y liberalización: cambios geográficos en la estructura económica brasileña”, en: Callicó, J., R. Bouchain et al. Insumo-producto regional y otras aplicaciones. México, UAM-A/UNAM/Universidad de Guadalajara, 2003, 454 pp.

Hewings, G. y R. Jensen. “Regional, interregional and multiregional input-output analysis”, en: Handbook of Regional and Urban Economics. Vol. 1. 1987, pp. 295-355.

Hurtado, A. y E. Martínez. “Redes binarias y la matriz insumo-producto: una aplicación regional”, en: Trayectorias. Año 19, núm. 45. 2017, pp. 57-76.

Jensen, R. “The concept of accuracy in regional input-output models”, en: International Regional Science Review. Vol. 5, núm. 2. 1980, pp.139-154.

Lenzen, M., A. Geschke, A. Malik, J. Fry, J. Lane, T. Wiedmann y A. Cadogan-Cowper. “New multi-regional input-output databases for Australia-enabling timely and flexible regional analysis”, en: Economic Systems Research. Vol. 29, núm. 2. 2017, pp. 275-295.

Leontief, W. “Input-Output Economics”, en: Scientific American. Vol. 185, núm. 4. 1951, pp 15-21.

Mariña, A. Insumo-producto: aplicaciones básicas al análisis económico estructural. México, UAM-Azcapotzalco, 1993.

Marto, A. L. Regional input-output tables and models: Interregional trade estimation and input-output modelling based on total use rectangular tables. Tesis doctoral. Facultad de Economía, Universidad de Coimbra, 2009.

Miller, R. y P. Blair. Input-Output Analysis: Foundations and Extensions. Cambridge, Cambridge University Press, 2009.

Oosterhaven, J. Rethinking Input-Output Analysis: A Spatial Perspective. Suiza, Springer, 2019.

_______ “The supply‐driven input‐output model: A new interpretation but still implausible”, en: Journal of Regional Science. Vol. 29, núm. 3. 1989, pp. 459-465.

Peters, G. P., R. Andrew & J. Lennox. “Constructing an environmentally-extended multi-regional input-output table using the GTAP database”, en: Economic Systems Research. Vol. 23, núm. 2. 2011, pp.131-152.

PROMÉXICO. Perfil del sector automotriz. 2016 (DE) https://bit.ly/3kw7RVp

Rose, A., y T. Allison. “On the plausibility of the supply‐driven input‐output model: Empirical evidence on joint stability”, en: Journal of Regional Science. Vol. 29, núm. 3. 1989, pp. 451-458.

Schuschny, A. Tópicos sobre el Modelo de Insumo-Producto: teoría y aplicaciones. Santiago de Chile, Naciones Unidas-CEPAL, 2005.

SEDATU. Metodología de la regionalización funcional en México. 2015 (DE) https://bit.ly/3zqeAX6

Tobler, W. “A computer model simulation of urban growth in the Detroit region”, en: Economic Geography. Vol 46, núm. 2. 1970, pp. 234-240.

_______ “Geographical Filters and Their Inverses”, en: Geographical Analysis. Vol. 1, núm. 3. 1969, pp. 234-253.

Torre, L., J. Alvarado y M. Quiroga. “Matrices insumo-producto regionales: una aplicación al sector automotriz en México”, en: Banco de México. Documentos de investigación. Julio del 2017.

______________

^[1] Programa estadístico del Instituto Nacional de Estadística y Geografía (INEGI).

^[2] Hoy alcaldías de la Ciudad de México.

^[3] Ambos reflejan de manera consistente las relaciones sectoriales en el entendido de que son precisamente los Censos Económicos una fuente de datos estadísticos que da sustento a la elaboración de la matriz insumo-producto nacional del 2013.

^[4] Aunque la construcción de regiones funcionales es un tema mucho más amplio, por sí mismo materia de investigación, la Secretaría de Desarrollo Agrario, Territorial y Urbano (SEDATU, 2015) propone que para delimitar regiones funcionales tienen que ser analizadas “… redes de circulación, flujos de personas, bienes e información económica y social, la cual se orienta a la determinación de estructuras económicas caracterizadas por convergencias de interacciones de diferentes órdenes entre la población y sus fuentes de empleo…” (p. 14).

^[5] En el argot del análisis exploratorio de datos y la econometría espacial se refiere a las estimaciones de indicadores globales o locales de asociación espacial basados en matrices de contigüidad tipo reina (Queen), que supone un vecindario similar al movimiento válido en todas direcciones que hace esa pieza de ajedrez.

^[6] El método empleado está descrito en Mariña (1993, pp. 71-73).

^[7] Esto significa que la matriz w_ij se construye considerando que cada unidad espacial comparte información, en lo referente a la contigüidad, con aquellas unidades espaciales que comparten una arista o un vértice; esto técnicamente está definido en un SIG.

^[8] Para ver de forma detallada el planteamiento de esta técnica, se recomienda el texto de Anselin (1995).