Standardization of Basic Urban Geostatistical Areas for 100 Cities of the National Urban System

 

Jorge A. Montejano Escamilla,* Gerardo Ávila Jiménez** y Camilo Alberto Caudillo Cos***
* Centro de Investigación en Ciencias de Información Geoespacial (CentroGeo), jmontejano@centrogeo.edu.mx
** Universidad Autónoma Metropolitana y CentroGeo, gavila@centrogeo.edu.mx
*** CentroGeo, ccaudillo@centrogeo.edu.mx

Nota: trabajo realizado con el apoyo financiero del proyecto Fondo Sectorial INEGI-CONACYT (S0025-2016-1), solicitud núm. 278953.

Vol. 11, Núm. 3 – Epub                                 Estandarización…  – Epub

En los últimos años se ha incrementado de forma considerable el número de estudios espaciales que utilizan las áreas geoestadísticas básicas (AGEB) como referente geográfico de los datos censales en nuestro país, los cuales produce el Instituto Nacional de Estadística y Geografía. En el proyecto Forma Urbana y Productividad en México 1995-2015 —desarrollado por el Centro de Investigación en Ciencias de Información Espacial— se utilizaron, primero, para calcular la superficie urbana y, después, la expansión urbana en el tiempo y algunas métricas adicionales de forma urbana para las 100 ciudades más grandes del Sistema Urbano Nacional 2010 entre 1995 y el 2015. Las comparaciones entre las AGEB, realizadas en cinco fechas censales, arrojaron inconsistencias topológicas (i. e. desfases y deformaciones cartográficas), por lo que se tuvieron que corregir las bases de datos para dar certidumbre a los resultados. En este trabajo se presenta el procedimiento utilizado en el ajuste espacial y la corrección topológica de las AGEB. Palabras clave: ajuste espacial; topología y datos espaciales.

In recent years there has been a considerable increase in the number of spatial studies that use basic geostatistical areas (AGEB) as a geographical reference for census data in our country, which are produced by the National Institute of Statistics and Geography. In the project Urban Form and Productivity in Mexico 1995-2015 –developed by the Center for Research in Geography and Geomatics– were used, first, to calculate the urban area and then, the urban expansion in time and some additional metrics of urban form for the 100 largest cities of the National Urban System 2010 between 1995 and 2015. Comparisons between AGEBs, carried out on five census dates, showed topological inconsistencies (i.e. lags, and cartographic deformations), so the databases had to be corrected to give certainty to the results. In this paper we present the procedure used in the spatial adjustment and topological correction of the AGEB.                                                                                                                                                   Key words: spatial adjustment; topology and spatial data.

Recibido: 11 de octubre de 2019.
Aceptado: 27 de febrero de 2020.

 

Introducción

El Centro de Investigación en Ciencias de Información Geoespacial (CentroGeo) logró apoyo financiero del Fondo Sectorial INEGI-CONACYT con el objetivo de probar diversas hipótesis sobre la relación entre forma urbana y productividad laboral (medida como valor agregado censal bruto/trabajador). La idea central planteaba que las ciudades compactas tienden a ser más eficientes que las más dispersas. Lo anterior es argumentado en literatura científica proveniente sobre todo de países con economías avanzadas y basadas en su mayoría en servicios. Para ahondar en la propia investigación, sus métodos y resultados, consultar Montejano et al. (2020) y Montejano et al. (2019).

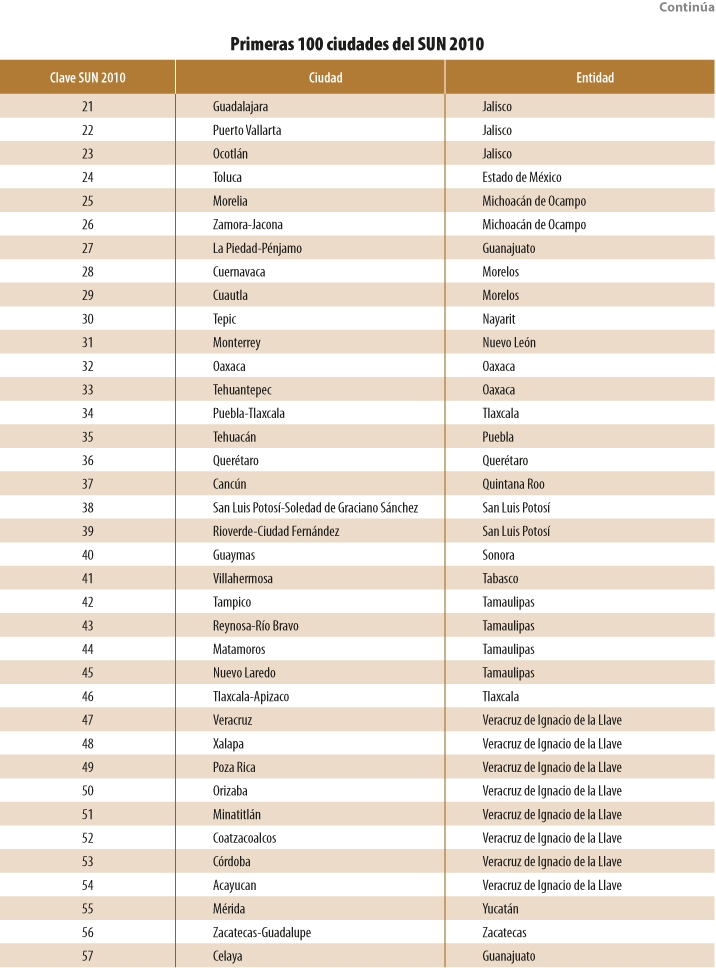
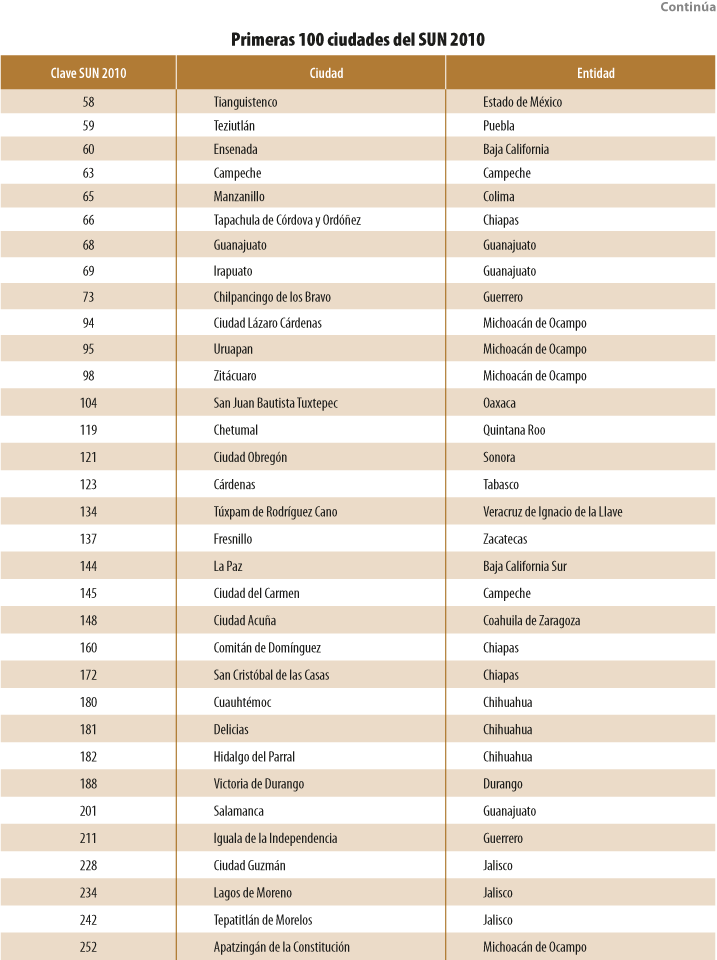
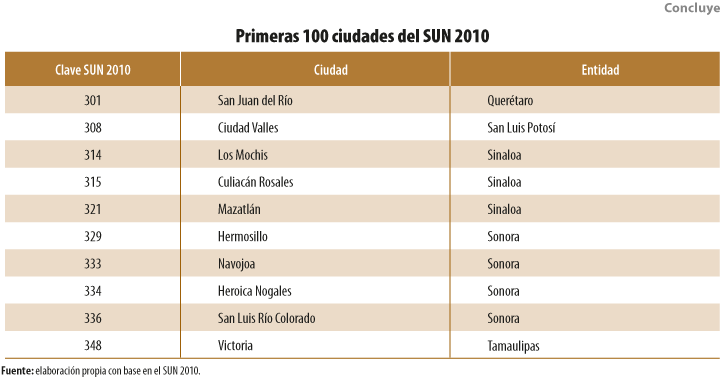
La estrategia de investigación consistió en cuantificar las trasformaciones de las 100 ciudades más grandes del Sistema Urbano Nacional (SUN) 2010 en el tiempo y, posteriormente, verificar el grado y signo de correlación con la productividad laboral observada. La unidad básica para cuantificar los cambios fue el área geoestadística básica (AGEB),^[1] que se utilizó para generar las métricas para 1995, 2000, 2005, 2010 y el 2015 (ver cuadro 1). Los resultados de la investigación son relevantes para la política pública territorial nacional ya que, con base en ellos, es posible matizar las políticas actuales en materia de ordenamiento del territorio, plasmadas en la mayoría de los programas de desarrollo urbano municipales que promueven la ciudad compacta como santo grial sin tomar en cuenta la base económica que representa la manufactura en México y que está presente en muchas de las urbes del país analizadas, pues sigue siendo la actividad más productiva, pero su principal activo es la localización exurbana, en zonas con relativo bajo precio del suelo y alta accesibilidad a la red carretera.

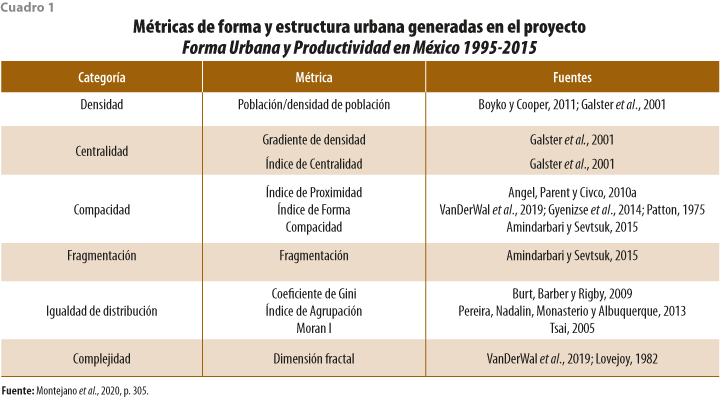
Dada la gran cantidad de métricas a generarse para alimentar nuestro modelo de panel con base en la unidad AGEB,^[2] fue indispensable revisar la consistencia espacial de las bases de datos generadas por el INEGI para reducir la incertidumbre en el modelaje.

En un ejercicio previo, el equipo ya había detectado errores en la variable crecimiento urbano dentro de una base de datos longitudinal 1990-2010. En ella, observamos que existían ciudades del SUN que, en lugar de crecer en tamaño, se hacían cada vez más pequeñas. Este hallazgo nos dio una pista sobre un posible error topológico en la base de datos generada a partir del Marco Geoestadístico Nacional (MGN) del INEGI en sus diferentes ediciones, disponibles en línea y con las que se generó el panel. Por lo anterior, fue necesario —antes de la generación de indicadores y armado del panel 1995-2015— realizar las tareas de ajuste espacial y corrección topológica de los datos geográficos por AGEB del propio MGN. En la segunda etapa se planteó la corrección de estas situaciones para que los índices espaciales generados a partir de la información cartográfica fueran lo más robustos posible.

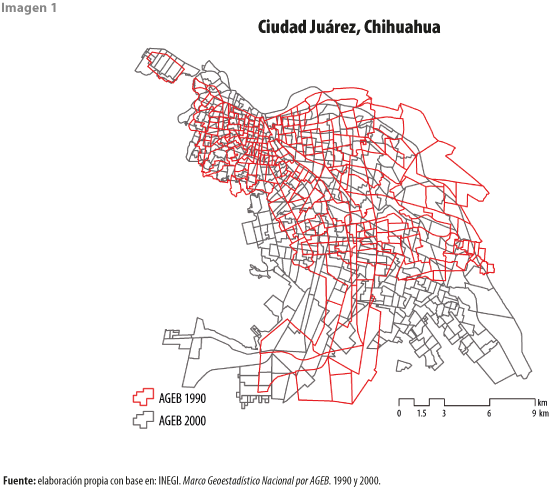
En las imágenes 1 y 2 se muestran algunas de las múltiples inconsistencias detectadas en la cartografía censal utilizada, la cual fue entregada directamente por el INEGI a CentroGeo y que se asumía podría haber generado resultados erróneos en las métricas. En ellas se puede apreciar que existe rotación, desplazamiento y, en algunos casos, una reducción en el tamaño de las AGEB, errores considerables como para poner en duda cualquier resultado analítico proveniente de estos datos, máxime si el proceso analítico es espacialmente explícito.

Sobre el SUN y la elección de las 100 ciudades

Como lo definen el Consejo Nacional de Población (CONAPO) y la extinta Secretaría de Desarrollo Social (SEDESOL), el SUN es “… el conjunto de ciudades de 15 mil y más habitantes, que se encuentran relacionadas funcionalmente, y cualquier cambio significativo en alguna de ellas propicia, en mayor o menor medida, alteraciones en las otras…” (2012, p. 11). Se clasifica en diferentes tipos de urbes, las cuales comprenden zonas metropolitanas (agrupaciones de municipios que están muy relacionados funcional y físicamente, o centros urbanos de más de un millón de habitantes), conurbaciones (cuando dos o más localidades o centros urbanos tienen contigüidad física y forman una sola unidad de más de 15 mil habitantes) y centros urbanos (ciudades de 15 mil o más pobladores que no cumplen las dos anteriores características). La versión 2010 contaba, en su momento, con 384 ciudades de más de 15 mil habitantes (CONAPO y SEDESOL, 2012); en la del 2018 hay un total de 401 (SEDATU, 2018).

El SUN, en conjunto con las distintas ediciones de la serie Delimitación de zonas metropolitanas, desarrolladas en conjunto por CONAPO, SEDESOL y la Secretaría de Gobernación (SEGOB), constituyen una de las principales herramientas de clasificación y delimitación espacial para la planeación del territorio en nuestro país. Ambos instrumentos dan cuenta de las transformaciones en las dinámicas exurbanas,^[3] de la creciente concentración de la población en núcleos urbanos y de la dispersión de gran cantidad de asentamientos humanos en el país. De allí la importancia del SUN y de la relevancia de tener una base de datos (MGN) confiable a nivel AGEB.

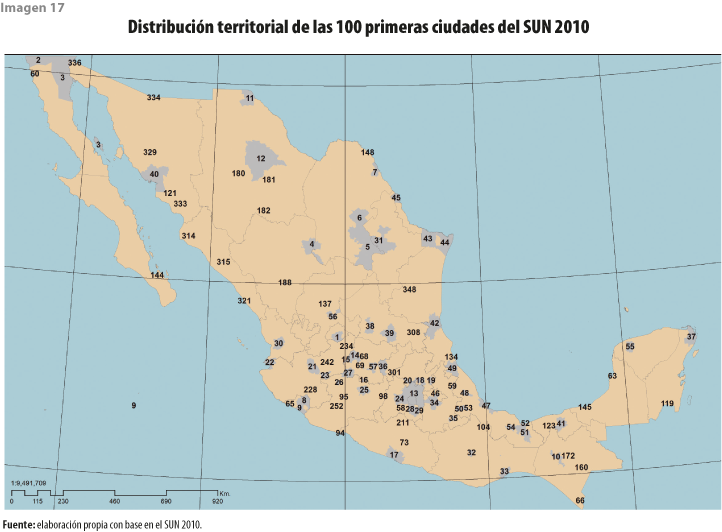
La razón por la cual determinamos utilizar como insumo en nuestra investigación las primeras 100 ciudades del SUN 2010 fue porque el conjunto de las primeras 93 (con población mayor a 100 mil habitantes) aportaron a la economía cerca de 90% de la Producción Bruta Total (PBT) del país en el 2009, concentrando también 83% del total de personal ocupado (ONU-Hábitat y SEDESOL, 2011, p. 27). Además, cerca de 60% de la población total del 2010 se encontraba repartida en las primeras 100 urbes. Con ellas se garantiza que la mayor parte de la PBT nacional esté cubierta.

Sobre la calidad de los datos espaciales

El problema de esta no es nuevo. Autores como Goodchild y Gopal (1989) o Gutpill y Morrison (1995) han tratado, desde hace tiempo, el tema de la precisión de los datos espaciales, incluyendo aquellos que van desde el linaje hasta el error.

Thapa y Bossler (1992) argumentan que su recolección es la fase más cara de la generación de un sistema de información geográfica (SIG), absorbiendo cerca de 80% del costo total, por lo que es muy importante contar con métodos lo más confiables posible; en ese trabajo, clasifican los tipos de errores más comunes en la recolección de datos geoespaciales, siendo los sistemáticos los que más se parecen a aquellos que hemos detectado en la serie del MGN del INEGI, los cuales muchas veces se deben a imperfecciones instrumentales y a limitaciones humanas; no importando su origen, ellos señalan que, en un sentido estadístico, este tipo de errores induce desviaciones en las observaciones (p. 836).

Por fuente de información, los errores que observamos en esta serie del INEGI pueden ser clasificados en métodos secundarios de colección de datos, es decir, las vías en que estos son recabados desde mapas, gráficas, cartas, etc. (Thapa y Bossler, 1992, p. 836). Los más comunes en los métodos secundarios de recopilación de información espacial son los introducidos en los dibujos, debido a una generalización del mapa, la calidad de reproducción, la deformación del material, la digitalización o escaneo, etcétera. Una gran parte de ellos puede observarse en la serie del MGN, aun cuando estos productos ya son de carácter digital. El hecho de que sean en este formato no implica en lo absoluto que sean exactos o precisos; Thapa y Bossler rematan señalando que “… la introducción de computadoras en el manejo de datos espaciales ha introducido una falsa sensación de precisión…” (p. 839).

Respecto a la precisión y la exactitud, es interesante resaltar que existe un concepto útil para reducir la carga negativa que implica la generación de errores en los datos espaciales. Es lo que Salgé define como precisión semántica: “… la cualidad con que los objetos geográficos son descritos en concordancia con el modelo seleccionado. Relativo al significado de ‘las cosas’ del universo del discurso (la realidad), la precisión semántica se refiere a la pertinencia del significado del objeto geográfico más que a su representación geométrica…” (1995, p. 10).

Es entonces que importa la precisión semántica, cuando un mismo objeto geográfico, con un nivel de precisión determinada, puede ser más o menos útil para un modelado dependiendo del objeto del propio modelado. En nuestro caso de estudio no importaría que los metadatos del objeto geográfico no estuvieran completos (por ejemplo, el método de generación), sino que es más relevante la precisión geométrica del objeto en relación con el paso del tiempo.

Supongamos que la serie de datos del año 1 tuviera un error que se repite tal cual en el año 2 hasta el n: es probable que, de mantenerse constante en todos los años, los resultados del modelo analítico serían consistentes en el tiempo, pues el error se hubiera acumulado de forma histórica. Sin embargo, cuando este pasa del año 1 al n mutando, por ejemplo, su forma geométrica (como en el caso de las imágenes 1 y 2), entonces se tiene un problema de certidumbre en el modelo analítico que no es aceptable y, por ende, es necesario enmendarlos.

Por ello, una primera tarea del grupo de investigación fue realizar el ajuste espacial y la corrección topológica de la cartografía censal del MGN para las 100 ciudades más grandes del SUN 2010 (ver Anexo A) en 1995, 2000, 2005, 2010 y el 2015. Suponemos que este trabajo —ya en manos del INEGI al momento de redactarlo— aumenta el valor agregado de los productos del Instituto al reducir errores topológicos, aumentar la confiabilidad de los resultados de análisis posteriores y orientar y proponer a la institución sobre el método o métodos a utilizarse para corregir todas las series del MGN. Partimos de la base de que este reporte del método utilizado abonará al objetivo que tiene trazada Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía, el cual es “… propiciar el intercambio de experiencias relevantes […] relativas al estado del arte en la generación de información estadística y geográfica…”.

Es interesante resaltar el hecho de que, al ser nuestra investigación explícitamente espacial, tuvimos especial cuidado en observar posibles errores relacionados con el territorio. Sin embargo, no sabemos cuántos estudios longitudinales que han utilizado este MGN y que no son como el nuestro —es decir, que no generan métricas donde la geometría ni la geografía importan a priori— circulan en la actualidad en el mundo académico, acarreando errores derivados de la utilización de cocientes que usan el territorio como denominador (i. e. densidades).

Materiales y métodos

El proceso inicial del ajuste espacial comenzó con la solicitud al INEGI de las distintas ediciones del MGN para la consulta de las AGEB con el objetivo de garantizar la calidad y consistencia de los datos. Una vez consolidado el banco de datos y seleccionadas las AGEB de cada una de las 100 ciudades más grandes del SUN 2010, se aplicaron diversos métodos, los cuales se describen en este apartado.^[4]

Como principal fuente de datos cartográficos de las AGEB fue considerado el MGN para 1995, 2000, 2005, 2010 y el 2015.

De manera paralela a la solicitud de información, se obtuvieron capas por medio de descarga directa en el portal (2010 y 2000), las cuales se utilizaron para realizar las primeras pruebas de similitud entre proyecciones cartográficas. El resultado de este proceso desechó el supuesto que plantea que el desfase cartográfico era originado por la definición de proyecciones cartográficas diferentes y particulares de cada capa y fecha consultada.

Se reproyectaron todas y cada una de las capas a un sistema de coordenadas geográficas, sin lograr un mejor ajuste espacial entre ellas.^[5] Durante la revisión de los datos, se detectó en la capa del 2000 la existencia de un desfase de las AGEB urbanas del estado de Colima; polígonos que se movieron utilizando puntos de control en función de su correspondencia geográfica con los polígonos de localidad; además, se identificaron 346 AGEB que fueron eliminadas por estar duplicadas en las bases geográficas.

Las pruebas realizadas en función de la proyección cartográfica no resultaron favorables: los desfases se mantuvieron, aun cuando a cada capa se le asignó un Datum ITRF92.

Con esta comprobación se confirmó —con base en una respuesta por escrito del propio Instituto— la existencia de desfases al sobreponer las capas de información de las AGEB obtenidas del MGN versiones 1995 y 2000 con las actuales. Dicha situación no fue posible solucionarla debido a que las capas no fueron modificadas a partir de ortofotos o versiones actualizadas del Marco Geoestadístico por escapar a la tarea central de la investigación y por no estar contemplada esta tarea en los términos de referencia.

Además, las AGEB de 1995 y el 2000 se obtuvieron de los planos incluidos en los productos del Sistema para la Consulta de Información Censal (SCINCE) 2010, los cuales no están georreferidos y fueron elaborados a mano alzada, esto es, no tienen una base raster ortorrectificada. Estos archivos fueron trabajados con los siguientes procesos:

• Conversión de formato dxf a formato Shapefile.
• Asignación de sistema global de coordenadas (UTM).
• En algunos casos se reubicó la localidad a su espacio correspondiente.
• Edición de polígonos de AGEB para eliminar huecos y traslapes.
• Obtención de polígonos de localidad a partir del proceso anterior.
• Reproyección a CCL-ITRF 1992.
• Edición de localidades a nivel nacional con el fin de corregir posibles traslapes parciales o totales entre ellas, siempre y cuando el proceso de edición fuera mínimo.

Derivado de lo anterior, y de que en principio los planos no fueron creados para integrarse en un SIG, los archivos originales (sin ajuste espacial) presentan las siguientes características:

• Traslapes entre localidades.
• No uniformidad en la escala de la localidad.
• Los archivos no tienen un comportamiento homogéneo en la asignación de capas; puede darse el caso de que un elemento esté en más de una de ellas.
• No cumplen con reglas topológicas (conexión, traslapes, duplicados).
• Carecen de metadatos.

Una vez que se tuvo completa la serie cartográfica, se evaluó la pertinencia de utilizar el año 1990 como una capa más en el estudio. En esta evaluación se consideró que presentaba una gran disparidad con respecto a los años posteriores y que aumentaría el tiempo de dedicación para su ajuste espacial, además de que, para ese periodo, no se cuenta con información estadística de tipo económica. Por tal motivo, la serie cartográfica utilizada fue quinquenal, iniciando en 1995 y finalizando en el 2015.

Con la serie completa de las AGEB, se iniciaron las pruebas que se utilizaron para definir el proceso de estandarización de las capas del MGN. De forma inicial, se evaluó la herramienta Modify-Stretch Multiple de AutoCad, la cual permite mover, escalar y expandir o contraer polígonos.

Este proceso implicó exportar la cartografía de las 100 ciudades correspondientes a las cinco fechas seleccionadas en formato DWG. Como prueba inicial se trabajaron las 10 primeras del SUN 2010 para cada periodo (ver Anexo A). Los resultados no fueron los deseados, ya que prevalecieron los desfases ocasionados por la limitada capacidad de ajuste que brinda la herramienta. Por lo tanto, se determinó que los resultados no garantizaban una adecuada calidad de la información.

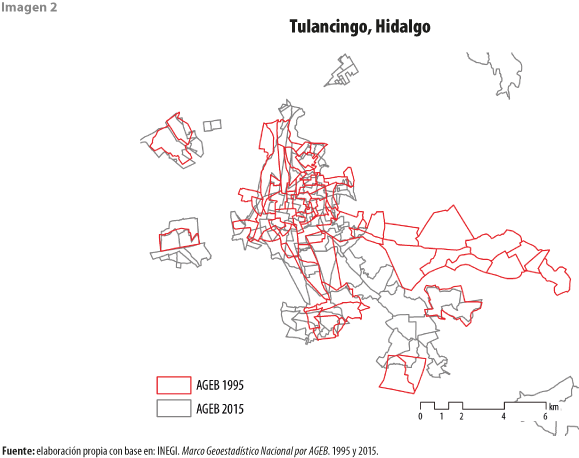
Una vez desechada la posibilidad de utilizar la herramienta antes descrita, se buscaron dentro de la caja de ArcGis métodos que garantizaran mejores ajustes espaciales. Para ello, se consultó la sección del escritorio de ayuda de ArcGis 10.2 y se retomó el esquema de la imagen 3.

Las principales funciones de transformación disponibles en ArcGis 10.2 se basan en la comparación de las coordenadas de puntos de origen y destino (también llamados puntos de control) con elementos gráficos espaciales denominados vínculos de desplazamiento. Se crearon vínculos de forma interactiva apuntando a ubicaciones de origen (por ejemplo, AGEB 1995) y destino conocidas (AGEB 2000).

Los métodos para el ajuste espacial que dispone ArcGis 10.2 (ArcMap, s/f) son:

• Transformación afín (transformation affine).
• Transformación de similitud (transformation similarity).
• Transformación proyectiva (transformation projective).
• Media cuadrática y residual (Rubbersheet).
• Transformaciones ciegas (Edge Snap).

A continuación, se describe cada uno de ellos, así como los resultados del proceso de ajuste espacial para el caso de una zona de la ciudad de Aguascalientes.

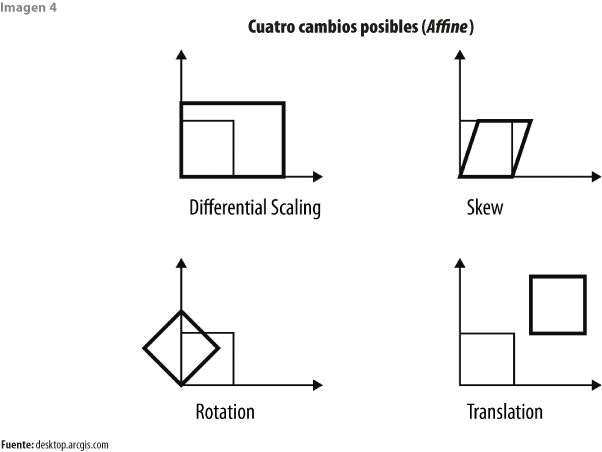
•  Transformación afín (Affine). Puede escalar los datos diferencialmente, sesgarlos, rotarlos y traducirlos. Su función es:

x’ = Ax + By + Cy’ = Dx + Ey + F

donde: x y y son las coordenadas de la capa de entrada y x’ y y’ son las coordenadas transformadas. A, B, C, D, E y F se determinan comparando la ubicación de los puntos de control de origen y destino. Escalan, sesgan, rotan y traducen las coordenadas de la capa. Este método requiere un mínimo de tres vínculos (ver imagen 4).

• Transformación de similitud (Similarity). Escala, rota y traduce los datos. No escalará los ejes de forma independiente ni introducirá ningún sesgo. Se mantiene la relación de aspecto de las entidades transformadas, lo cual es importante si se desea mantener la forma relativa de las entidades.

        Su función es:

                                  x’ = Ax + By + Cy’ = -Bx + Ay + F

donde:   A = s * cos t

B = s * sen t

C = traslación en dirección x

F = traslación en dirección y

s = cambio de escala (similar en las direcciones x, y)

t = ángulo de rotación, medido en sentido contrario a las manecillas del reloj desde el eje x

Requiere un mínimo de dos vínculos de desplazamiento; sin embargo, se necesitan por lo menos tres para que se produzca un error cuadrático medio (ECM).

 

• Transformación proyectiva (Projective). Se basa en una fórmula más compleja que requiere un mínimo de cuatro vínculos de desplazamiento:

x’ = (Ax + By + C) / (Gx + Hy + 1) y’ = (Dx + Ey + F) / (Gx + Hy + 1)

Este método se utiliza para transformar los datos capturados directamente de la fotografía aérea.

• Media cuadrática y residual (Rubbersheet). Los parámetros de transformación son un mejor ajuste entre los puntos de control de origen y destino; si se utilizan para transformar los puntos de control de origen actuales, las ubicaciones de salida transformadas no coincidirán con las de puntos de control de salida reales; esto se conoce como error residual y es una medida del ajuste entre las ubicaciones reales y las transformadas de los puntos de control de salida (ver imagen 5).

 

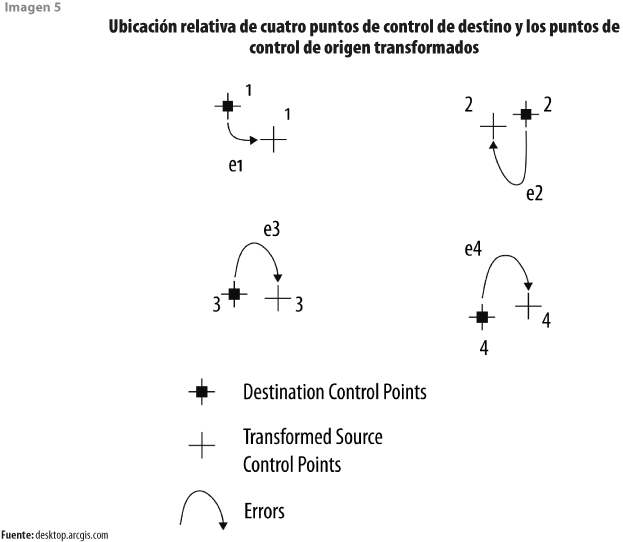
El ECM mide las fallas entre los puntos de control de destino y las ubicaciones transformadas de los puntos de control de origen:

La transformación se obtiene a partir de mínimos cuadrados, por lo que se pueden proporcionar más vínculos de los necesarios; hay que especificar un mínimo de tres para obtener una transformación que dé lugar a un ECM. Por lo general, cuantos más vínculos ubique para una transformación, más precisa será.

• Transformaciones ciegas (Edge Snap). Es posible configurar la transformación creando vínculos de desplazamiento con el extremo de origen en ubicaciones conocidas y el extremo de destino en puntos en el espacio temporales. Después de esto, podrá utilizar la tabla de vínculos para editar las coordenadas de destino de estos vínculos y que pasen a ser las ubicaciones del mundo real correspondientes.

Procesamiento

Este apartado presenta el proceso desarrollado para seleccionar el método que dio el mejor ajuste espacial en las series de datos espaciales para su posterior corrección topológica. Se aplicaron cuatro de los cinco métodos citados en la sección anterior. El Edge Snap se omitió debido a que requiere mayor tiempo y trabajo destinado en la asignación manual de valores conocidos x, y necesarios para lograr el ajuste espacial.

Ajuste espacial

Para seleccionar el método que garantizare el mejor ajuste espacial, se aplicaron los cuatro métodos a las primeras 10 ciudades del SUN. Se definieron dos criterios para escoger el mejor método de ajuste espacial: 1) correspondencia en su forma, que considera mayor similitud geométrica entre la capa ajustada con la de referencia (valoración visual) y 2) mayor proporcionalidad de la superficie obtenida en la capa ajustada espacialmente con respecto a la superficie de la capa de referencia (valoración proporcional), es decir, qué tanto se parecen las superficies. Para fines ilustrativos, solo se presenta una porción de la ciudad de Aguascalientes, ejemplificando la aplicación de los criterios antes mencionados.

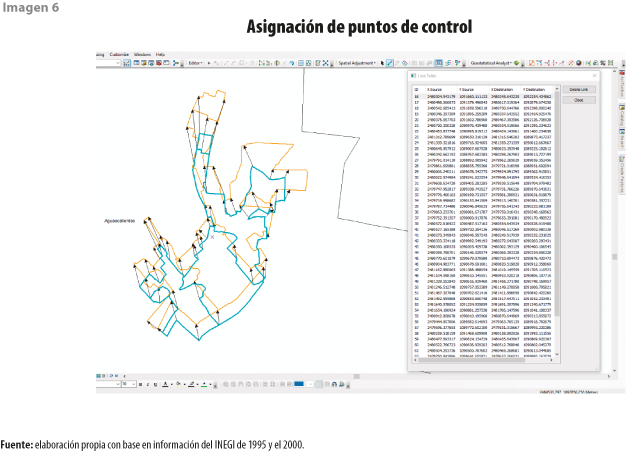
Como primer paso para la aplicación de cualquiera de los cuatro métodos, fue necesario asignar los puntos de control en la capa por ajustar, con respecto a la capa de referencia (ajustar 1995 con referencia a la 2000), para cada una de las zonas seleccionadas (ver imagen 6).

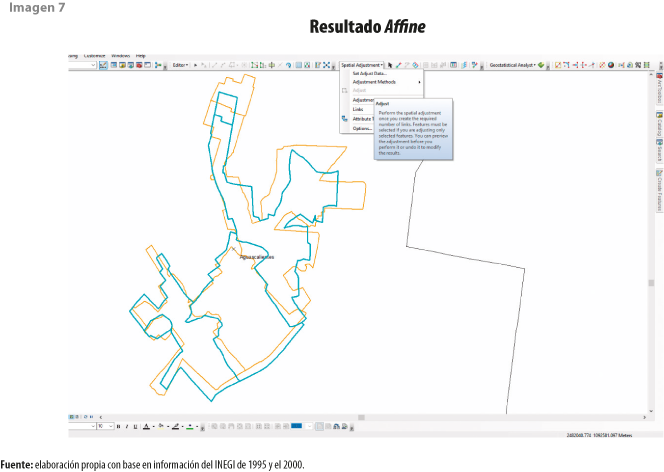
Una vez que se han asignado los puntos de control, se ejecutan los métodos de ajuste espacial disponibles en ArcGis10.2 de la siguiente manera: abrir en el menú secundario Spatial Adjustment y seleccionar el método de transformación, en este caso el Affine y, posteriormente, Adjust (ver imagen 7).

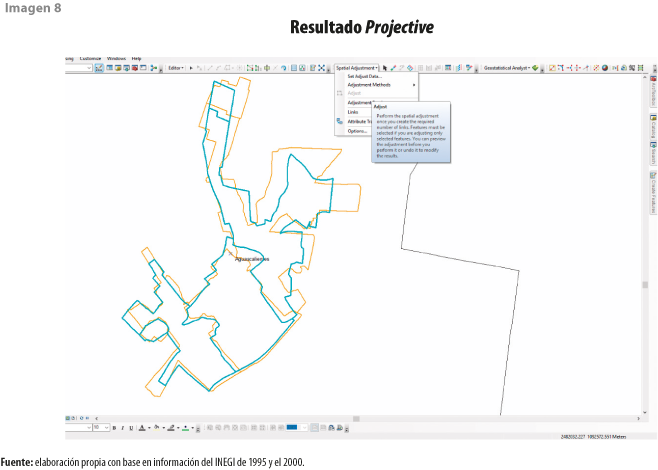
Enseguida, abrir en el menú secundario Spatial Adjustment y seleccionar el método de transformación Projective y, después, Adjust (ver imagen 8).

 

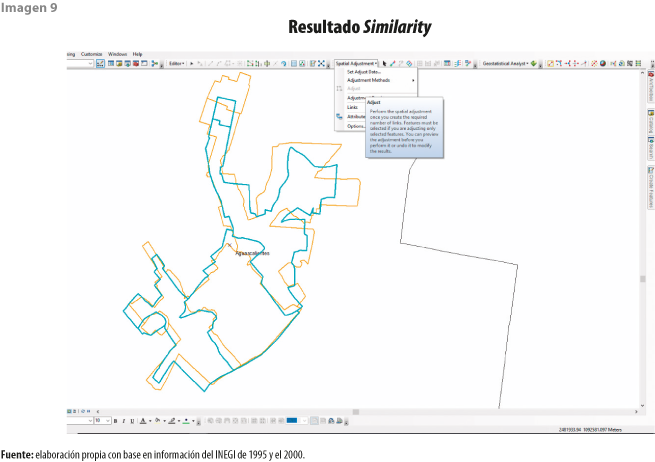
Después, abrir en el menú secundario Spatial Adjustment y seleccionar el método de transformación Similarity y, enseguida, Adjust (ver imagen 9).

Para seguir, abrir en el menú secundario Spatial Adjustment y seleccionar el método de transformación Rubbersheet y dar clic en Adjust (ver imagen 10).

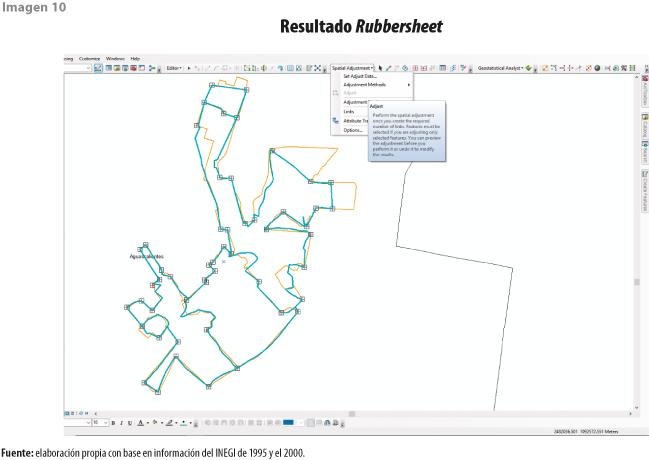
A manera de ejemplo, y con base en la aplicación de los criterios, se logra un mejor ajuste espacial en función de la valoración visual con el método Rubbersheet (ver imagen 10) que con los otros tres. En términos de proporcionalidad, la superficie ajustada representa 96% con respecto a la total de las AGEB de referencia. Los otros métodos obtuvieron proporcionalidades por debajo de este porcentaje.

Con base en la aplicación del método Rubbersheet se obtuvo un mejor ajuste espacial, por lo que fue seleccionado y aplicado para la transformación de las cuatro capas cartográficas anteriores al 2015 para cada una de las 100 ciudades del SUN. Este se realizó en dos momentos: 1) en el proceso que inició con el ajuste de la capa de AGEB 1995 con referencia a la capa del 2000, y de manera sucesiva hasta llegar al del 2010 respecto al 2015 y 2) utilizando las capas previamente ajustadas (resultado del proceso anterior). Las modificaciones se realizaron ahora en sentido inverso, tomado como referencia las AGEB 2015, para ajustar el 2010 de manera sucesiva hasta completar todos los de las capas posteriores. Como respaldo a los criterios considerados en este proceso, se utilizaron como referencia imágenes satelitales^[6] (procurando la correspondencia con las fechas de las capas), sobre todo para ajustar las AGEB periurbanas. Cabe señalar que las modificaciones a este tipo de polígonos requirieron de mayor dedicación para subsanar un mayor número de deformaciones geométricas, sobreescalamiento y sobredelimitaciones que incluyen territorios no urbanizados.

Corrección topológica

Una vez que se revisaron y ajustaron los polígonos de las AGEB (1995, 2000, 2005 y 2010), se obtuvieron las capas de información geográfica en formato shapefile para su revisión y corrección topológica. La topología garantiza la calidad de la información debido a que permite obtener entidades de polígonos que comparten una geometría coincidente, es decir, deben tener límites comunes; además, incluye un modelo de datos topológicos que permite integridad, en un formato de almacenamiento abierto, reglas y coordenadas integradas entre las entidades con geometría compartida.

Para el uso de la herramienta topology de ArcGIS 10.2, se obtuvo un archivo geodatabase (gdb) compuesto por los archivos dataset (conjunto de datos) de cada una de las capas de las AGEB corregidas espacialmente. Con base en el conjunto de datos antes mencionado, el siguiente paso fue crear la topología para cada dataset, bajo los criterios de sobreposición y espacios entre polígonos, cuyos resultados son útiles para identificar errores y excepciones, que serán las principales referencias para consultar, editar, validar y corregir los errores identificados en las topologías obtenidas. ArcGIS 10.2 cuenta con un marco de edición y automatización de datos que se utiliza para crear, mantener y validar la integridad topológica y para editar entidades compartidas.^[7]

A continuación, se presentan los reportes del proceso topológico para cada una de las capas de las AGEB, señalando el total de errores topológicos divididos en fallas de superposición de polígonos y por separación entre polígonos.

El total de los errores topológicos se muestran en la imagen 12.

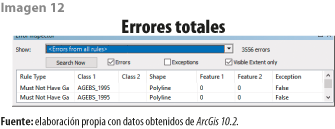
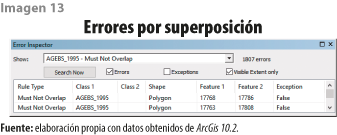
Los errores detectados para este ejemplo por sobreposición de polígonos corresponden a 51% del total de los detectados (ver imagen 13).

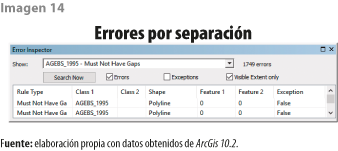
Del total de errores identificados, 49% corresponde a separaciones entre polígonos; no obstante, hay que descontar de esta proporción aquellas separaciones naturales existentes entre ciudades (ver imagen 14).

Al final, para cada conjunto de datos, se revisaron y corrigieron todos y cada uno de los errores por superposición, así como por separación entre polígonos dentro de los límites de las 100 ciudades para cada una de las cinco capas geográficas.

Resultados

Lo obtenido en las capas ajustadas correspondientes a 1995, 2000, 2005, 2010 y el 2015 es satisfactorio de acuerdo con el criterio de valoración visual (ver imagen 15), que tal vez sea el que representa un mayor esfuerzo y reafirma que el método debe ser supervisado. De forma paralela, se realizó el cálculo de las superficies por cada una de las ciudades ajustadas, poniendo mayor atención a las que en las capas originales reportaron una disminución de su superficie en una fecha posterior.

En términos generales, con el ajuste espacial se mejoró la forma y correspondencia espacial de los polígonos de las AGEB; además, se corrigieron las superficies de aquellas ciudades que se comprimían.

 

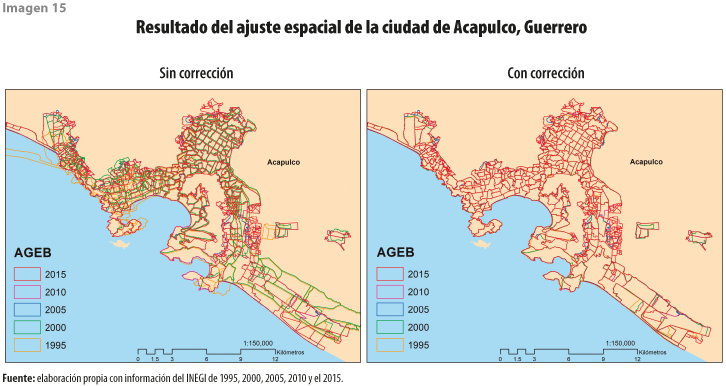
Comparación cartográfica con ajuste espacial

Si bien no existe una medida precisa para conocer el grado de ajuste espacial entre la capa origen con la ajustada, se optó por generar estadísticos descriptivos que dieran idea de la variabilidad de los datos de superficie y perímetro (forma). Al revisar las capas de las AGEB originales (tomadas directamente del INEGI), se encontraron errores topológicos por sobreposición, duplicidad y separación de polígonos.

Las pruebas se realizaron utilizando las variables de superficie en hectáreas y el perímetro en kilómetros en dos escalas:

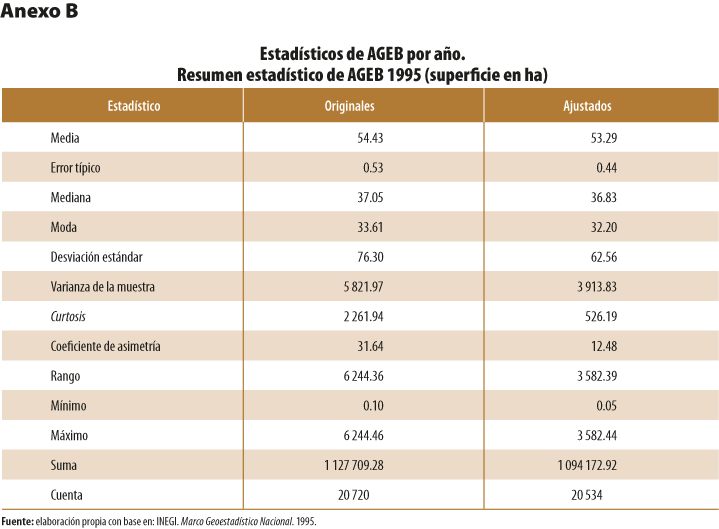
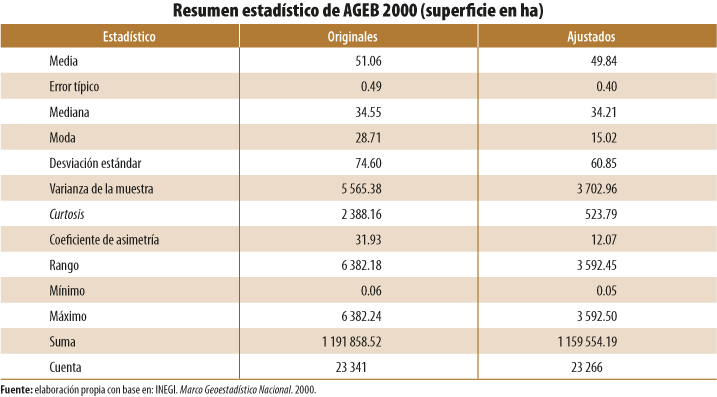
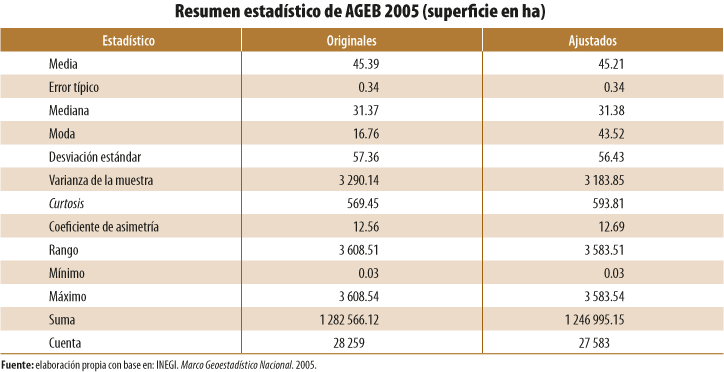
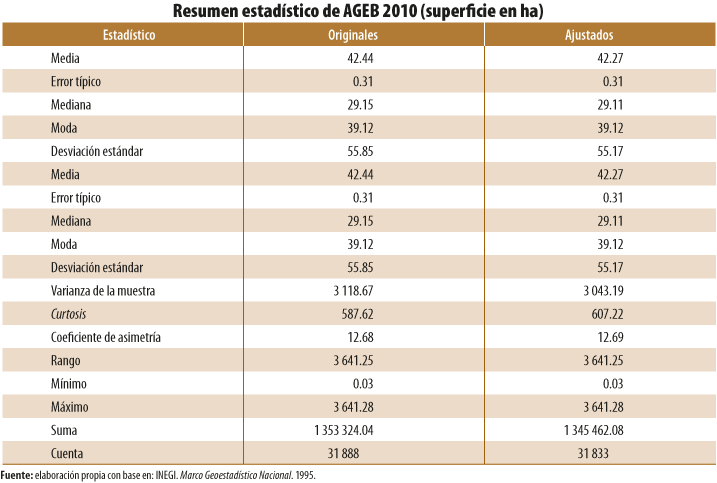
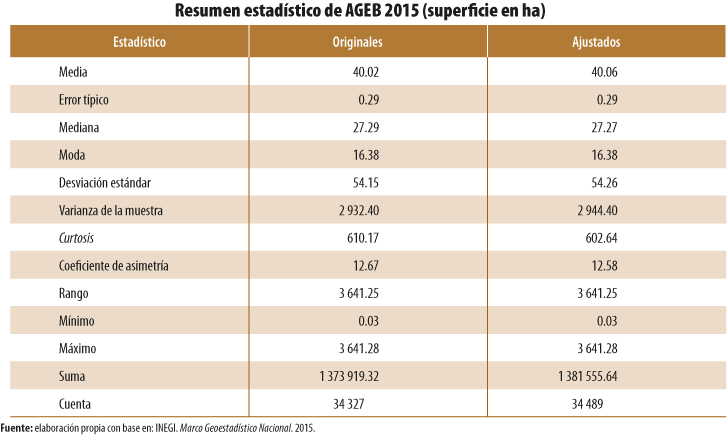
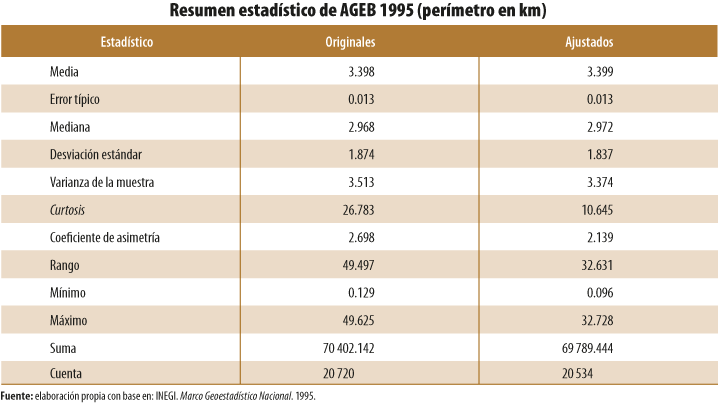
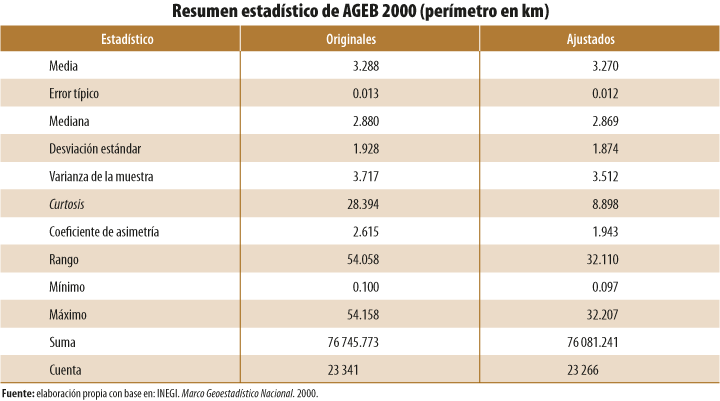
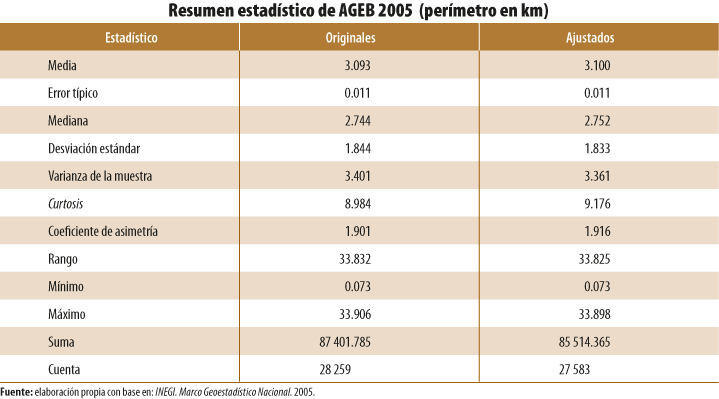
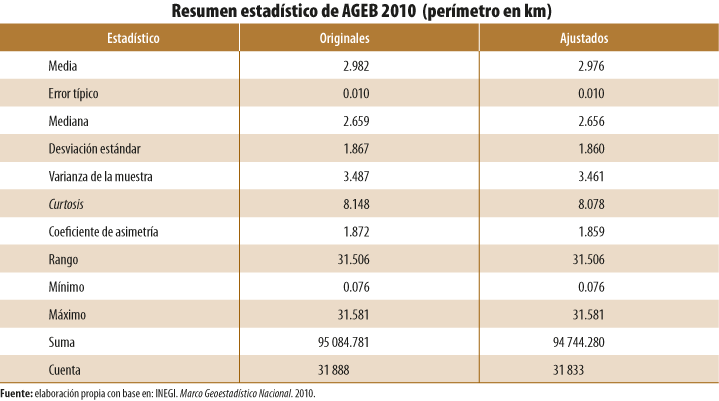
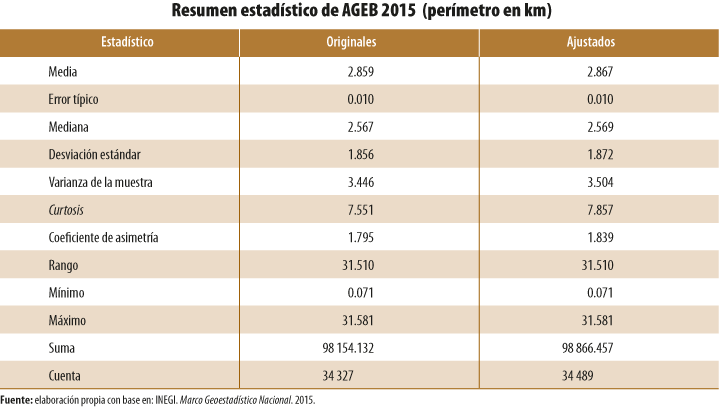
• A nivel de AGEB, se analizaron en su totalidad los polígonos geoestadísticos que forman una capa geográfica en un año específico (1995, 2000, 2005, 2010 y el 2015). Para realizar comparaciones respecto a los cambios entre la capa original y la ajustada de un mismo año, se generaron estadísticos descriptivos (ver Anexo B).
• Para comparar los cambios tanto en la superficie como en la forma en nivel ciudad, se utilizaron los polígonos de las 100 ciudades de cada año a través de una medida de razón perímetro-área (RPA).

Para el primer caso, los estadísticos que se utilizaron para comparar los cambios fueron: la desviación estándar y la media aritmética para obtener el coeficiente de variación (CV),^[8] además de la medida de curtosis para ver el afilamiento de la curva de distribución del conjunto de datos y el sesgo o asimetría de los mismos.

En términos generales, las capas geográficas que registraron mayores cambios de acuerdo con sus CV (superficie y perímetro) correspondieron a 1995 y el 2000. Las principales causas que originaron cambios significativos en sus estadísticos fueron la corrección de polígonos duplicados y sobredimensionados correspondientes, sobre todo, a polígonos periféricos de las ciudades.

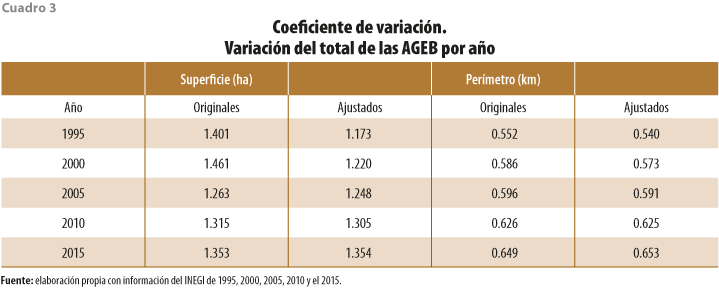
De forma paralela, en todos los casos analizados se mantuvo una asimetría positiva con sesgo a la derecha, con mejoría en su mayoría en las AGEB de 1995 y el 2000, considerando que el valor 0 indica que el conjunto de datos tiene una distribución simétrica. Las medidas de afilamiento o curtosis, obtenidas en todas las capas de AGEB ajustadas espacialmente, disminuyeron en términos absolutos. Este comportamiento demuestra que, mediante el ajuste del conjunto de las AGEB, estas continúan con una distribución en forma de pico por arriba de una curva normal estandarizada; sin embargo, el valor absoluto disminuyó, lo cual significa que su afilamiento se aplanó (ver Anexo B).

Los cambios posteriores al ajuste espacial de las ciudades analizadas en relación con su superficie y forma se muestran mediante los valores obtenidos del coeficiente de correlación lineal. Dicha métrica se considera como una medida que permite calcular el grado de asociación lineal entre dos variables cuantitativas (ciudades originales 1995 y ciudades corregidas 1995). Se dice que existe una asociación lineal perfecta cuando la correlación de la muestra es 1. Se trata de ver qué tan parecidos son los valores del RPA-original con el ajustado en un mismo año (ver imagen 16).

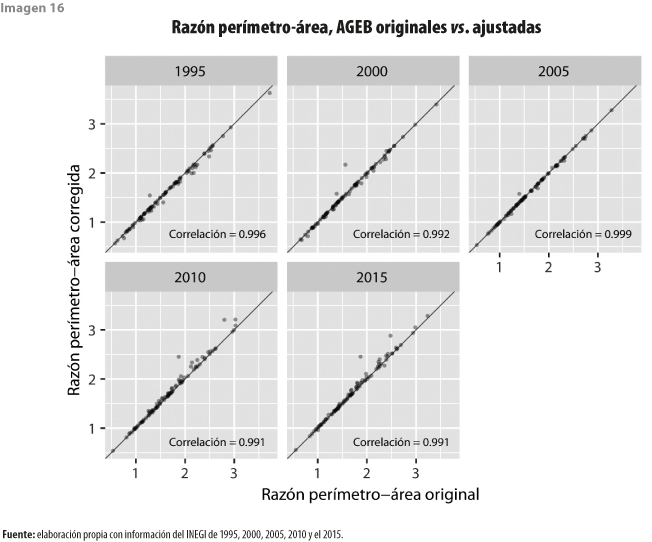
En términos generales, las ciudades que se encuentran alejadas de las líneas de ajuste son las que requirieron de mayores ajustes espaciales y su distancia refleja el grado de modificación del ajuste. Ciudades que se contraían, mediante el ajuste aumentaron tanto la superficie como el perímetro.

Conclusiones

En este trabajo se resumieron los procesos de ajuste espacial y corrección topológica mediante los cuales se corrigieron las ediciones del MGN a nivel AGEB para 1995, 2000, 2005, 2010 y el 2015 para las 100 ciudades más grandes del SUN 2010, lo que, a su vez, permitió correr un modelo longitudinal dentro del proyecto INEGI-CONACYT Productividad y Forma Urbana en México 1995-2015 que correlacionara crecimiento físico, forma urbana y productividad laboral con mayor certeza geoespacial.

Con lo anterior, se pone a consideración del INEGI el método utilizado de ajuste espacial y corrección topológica con el fin de que se aplique en el resto de las ciudades del SUN para los periodos ya mencionados.

Con el método propuesto, se obtienen archivos vectoriales que integran un sistema único de carácter nacional diseñado por el INEGI para diversos años, ajustado espacialmente y corregido en su topología, con el propósito de garantizar comparabilidad espacial con productos similares de otros años.

Para el proceso de ajuste espacial de las AGEB se utilizó el software ArcGis 10.2. El método seleccionado fue el Rubbersheet, el cual permite la transformación para un mejor ajuste entre los puntos de control de origen y destino.

Por su parte, la corrección topológica se realizó una vez concluido el proceso de ajuste espacial de los polígonos (AGEB), mediante el cual se obtuvo una capa de información geográfica en formato shapefile para su revisión y corrección topológica para, después, generar un modelo de datos topológicos (que permite integridad) en un formato de almacenamiento abierto, reglas topológicas y coordenadas topológicamente integradas entre las entidades con geometría compartida.

Los productos obtenidos son cinco capas geográficas estandarizadas y ajustadas espacialmente, que permiten realizar comparaciones espacio-temporales y, sobre todo, obtener métricas de base espacial con mayor confiabilidad. Estos se entregaron al INEGI como parte del proceso de transferencia del conocimiento en el marco del ya mencionado Fondo Sectorial INEGI-CONACYT.

Los estadísticos obtenidos de la evaluación de las capas con ajuste espacial y corrección topológica muestran una mejoría en comparación con las bases espaciales de origen, por lo que, aun con errores derivados del nivel de precisión del trabajo geoespacial, se asume que esta nueva serie del MGN es, por mucho, mejor que trabajar de forma comparativa con las bases del MGN sin corregir.

Por último, debe mencionarse que se asume que existen otros métodos más precisos para corregir las desviaciones ya señaladas en las diferentes ediciones del MGN; sin embargo, también se presume que este método es mucho más económico al concentrarse más en una mayor precisión que en una exactitud superior.

 

____________

Fuentes

Amindarbari, R. y A. Sevtsuk. Metropolitan Form Analysis Toolbox for ArcGIS v 10.2 and v 10.3.1. City Form Lab. 2015 (DE) https://bit.ly/2SBCtqY

Angel, S., J. Parent y D. L. Civco. “Ten compactness properties of circles: Measuring shape in geography”, in: The Canadian Geographer/Le Géographe Canadien. 54(4), 2010, pp. 441-461.

Boyko, C. y R. Cooper. “Clarifying and re-conceptualising density”, in: Progress in Planning. 76(1), 2011, pp. 1-61.

Burt, J., G. Barber y D. Rigby. Elementary statistics for geographers. The Guilford Press, 2009.

CONAPO y SEDESOL. Sistema Urbano Nacional. México, CONAPO-SEDESOL, 2012.

ESRI. Acerca de las transformaciones de ajuste espacial. ArcMap. (s/f) consultado en https://bit.ly/3jFuwg5

Ewing, R., R. Pendall y D. Chen. Measuring sprawl and its impact. Smart Growth America, 2002.

Galster, G., R. Hanson, M. Ratcliffe, H. Wolman, S. Coleman y J. Freihage. “Wrestling sprawl to the ground: Defining and measuring an elusive concept”, in: Housing policy debate. 12(4), 2001, pp. 681-717.

Goodchild, M y S. Gopal. The accuracy of spatial databases. CRC Press, 1989.

Guptill, S. y J. Morrison. Elements of spatial data quality. Elsevier, 1995.

INEGI. Marco Geoestadístico Nacional. Áreas Geoestadísticas Básicas Urbanas. Encuesta Intercensal 2015. México, INEGI, 2015.

_______ Marco Geoestadístico Nacional. Áreas Geoestadísticas Básicas Urbanas. Encuesta Intercensal, versión 5.0; Censo de Población y Vivienda 2010. México, INEGI, 2010.

_______ Manual de cartografía geoestadística. Levantamiento. Censo de Población y Vivienda 2010. México, INEGI, 2010a.

_______ Marco Geoestadístico Nacional. Áreas Geoestadísticas Básicas Urbanas. II Conteo de Población y Vivienda 2005, versión 1.0. México, INEGI, 2005.

_______ Marco Geoestadístico Nacional. Áreas Geoestadísticas Básicas Urbanas. Censo General de Población y Vivienda 2000. México, INEGI, 2000.

_______ Marco Geoestadístico Nacional. Áreas Geoestadísticas Básicas Urbanas. I Conteo de Población y Vivienda 1995. México, INEGI, 1995.

Lovejoy, S. “Area-Perimeter Relation for Rain and Cloud Areas”, in: Science. 216(4542), 1982, pp. 185-187 (DE) https://doi.org/10.1126/science.216.4542.185

Montejano, J., C. Caudillo, P. Monkkonen, E. Guerra, J. M. Núñez, B. Garza, G. Ávila y S. Medina. “Urban Form and Productivity in México 1995-2015”, in: European Journal of Sustainable Development. 9(1), 2020, pp. 300-316.

Montejano, J., P. Monkkonen, E. Guerra y C. Caudillo. The costs and benefits of urban expansion: Evidence from Mexico, 1990-2010. Lincoln Institute of Land Policy, 2019 (DE) https://bit.ly/2Fag6pn

ONU-Hábitat y SEDESOL. Estado actual de las ciudades de México 2011. ONU-Hábitat-SEDESOL, 2011.

Pereira, R., V. Nadalin, L. Monasterio y P. Albuquerque. “Urban centrality: A simple index”, in: Geographical Analysis. 45(1), 2013, pp. 77-89.

Salgé, F. “Semantic accuracy”, in: Guptill, S. y J. Morrison. Elements of spatial data quality. Elsevier, 1995, pp. 139-151.

Thapa, K. y J. Bossler. “Accuracy of spatial data used information systems”, in: Photogrammetric Engineering & Remote Sensing. 58(6), 1992, pp. 835-841.

Tsai, Y. Travel-efficient Urban Form: A Nationwide Study of Small Metropolitan Areas. 2001.

VanDerWaal, J., L. Falconi, S. Januchowski, L. Shoo y C. Storlie. SDMTools: Tools for processing data associated withspecies distribution modelling exercises (Version 1.1-221.1) [R package]. 2019.

 

 

^[1] Clasificadas en: rurales y urbanas. Ambas unidades corresponden a la subdivisión de las áreas geoestadísticas municipales. Para este estudio solo se consideraron las últimas, que se definen como: “Área geográfica ocupada por un conjunto de manzanas que generalmente va de 1 a 50, perfectamente delimitadas por calles, avenidas, andadores o cualquier otro rasgo de fácil identificación en el terreno y cuyo uso del suelo sea principalmente habitacional, industrial, de servicios, comercial, etcétera, sólo se asignan al interior de las localidades urbanas”. (INEGI, 2010a, p. 8.).

^[2] Diversos autores, entre ellos Angel, Parent y Civco (2010) o Ewing, Pendall y Chen (2002) han hecho hincapié sobre que el urban sprawl o la dispersión urbana es un fenómeno multifactorial que no puede ser descrito solo con una variable, de allí el número de métricas.

^[3] Son las que contienen características urbanas, pero en un contexto de dispersión o que no están ligadas de forma directa a entornos urbanos consolidados.

^[4] Para ampliar sobre el método seleccionado, es posible consultar el Reporte técnico de la primera etapa del FOSEC en https://bit.ly/3jAzxqp. El apartado específico sobre el arreglo de las bases de datos se encuentra a partir de la página 93 bajo el título Anexo 2. Proceso de estandarización de la información geográfica de 100 ciudades en nivel de AGEB.

^[5] El sistema de coordenadas geográficas en el que se reproyectaron todas las capas fue North America Lambert Conformal Conic ITRF 1992.

^[6] World Imagery-Source: Esri, DigitalGlobe, GeoEye, Earthstar Geographics, CNES/Airbus DS, USDA, USGS, AEX, Getmapping, Aerogrid, IGN, IGP, swisstopo y el GIS User Community.

^[7] Para mayor información sobre la corrección de la topología en ArcGIS, consultar https://bit.ly/30IIvdY

^[8] Medida que se emplea para comparar la variabilidad de los datos (en este caso, la superficie) de dos capas geográficas: AGEB originales y ajustadas. A mayor valor, mayor variabilidad.