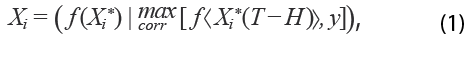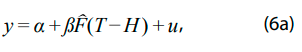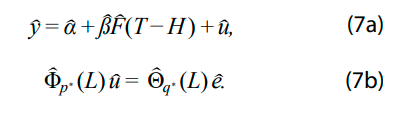Estimaciones oportunas para algunas variables relevantes de la coyuntura económica de México: implicaciones de corto plazo

 

Nowcasts for Relevant Mexican Macroeconomic Time Series:
Short Term Implications

 

Francisco de Jesús Corona Villavicencio,* Jesús López Pérez* y Pedro Paulo Orraca Romano**
* INEGI, franciscoj.corona@inegi.org.mx y jesus.lopezp@inegi.org.mx, respectivamente. 
** El Colegio de la Frontera Norte, porraca@colef.mx

Nota: los autores agradecen a Gerardo Leyva, director general adjunto de Investigación del INEGI, por sus excelentes comentarios y organización de las actividades de investigación que contribuyeron a mejorar este trabajo.

 

Vol. 12, Núm. 3 - EPUB                         Estimaciones oportunas... - EPUB

Mediante el uso de la metodología de Corona et al. (2021), en este trabajo se realizan estimaciones oportunas para algunas variables relevantes de la coyuntura económica de México, como las tres grandes actividades del Indicador Global de la Actividad Económica (IGAE), el consumo privado, la inversión fija bruta, así como las exportaciones e importaciones totales. Se concluye que esta metodología genera estimaciones precisas para dichas variables, excepto las del sector externo. Con base en este procedimiento, se consideran dos escenarios de crecimiento de la economía mexicana hasta diciembre del 2020, opuestos entre sí; en el primero, se espera que la tasa de crecimiento económica del IGAE anualizada sea de -12.7 % y en el segundo, se prevé un decremento de -8.8 por ciento. Promediándolos, nos otorgan un crecimiento esperado de -10.5 % en ese año. Palabras clave: ceteris paribus; COVID-19; escenario V; estimación oportuna; fuentes no tradicionales.

In this article we use the methodology by Corona et al. (2021) to carry out nowcasts for relevant Mexican macroeconomic time series, specifically the three grand economic activities of the Global Indicator of Economic Activity (IGAE in Spanish), private consumption, gross fixed investment, and total exports and imports. We conclude that this methodology generates precise estimations for such variables, with except of those of the foreign sector. The methodology allows, in turn, to consider two growth scenarios of the Mexican economy until December 2020, under the first scenario, the annualized growth rate of the IGAE for 2020 is expected to be -12.7% and in the second scenario a decrease of -8.8% is expected. By averaging both scenarios, we obtain an expected growth of -10.5% in 2020. Key words: ceteris paribus; COVID-19; V scenario; timely estimates; non-traditional information.

Recibido: 23 de octubre de 2020.
Aceptado: 23 de febrero de 2021.

 

Introducción

En marzo del 2020, la pandemia de COVID-19 llegó a México. Ante ello, el gobierno federal implementó diversas medidas sanitarias de distanciamiento social que incluyeron el cierre de escuelas, empresas, fábricas, oficinas de gobierno y la suspensión de actividades sociales y culturales. Su impacto económico se esperaba en una caída global de -9.9 % del Producto Interno Bruto (PIB) para el 2020;^[1] sin embargo, no se tiene certeza sobre la evolución que la economía tendrá en el corto plazo a nivel sectorial ni de cuál será la trayectoria para las componentes de la demanda agregada. Además, la generación de datos oficiales por las oficinas nacionales de estadística requiere apegarse a metodologías rigurosas que aseguren su calidad y comparabilidad internacional, las cuales conllevan múltiples tareas de captación, procesamiento y análisis; esto se traduce en que los indicadores duros se publiquen al menos con un mes de retraso.

En ese sentido, en la literatura existen modelos aplicados a la economía mexicana que buscan realizar estimaciones oportunas del PIB, por ejemplo, Delajara et al. (2016), Caruso (2018) y, de manera reciente, Gálvez-Soriano (2020). No obstante, los ejercicios previos utilizan primordialmente indicadores tradicionales de series macroeconómicas y financieras, lo cual limita su capacidad de capturar los efectos de corto plazo que pueden tardar en reflejarse en las series. Otra limitante de estos es que se enfocan en una variable trimestral, como es el PIB, porque lo que se requiere es desagregar dicha variable para conocer el estado de la economía en los meses intermedios. Para estos fines, se necesita una serie de tiempo de más alta frecuencia y que esté correlacionada con el PIB (ver, por ejemplo, a Guerrero y Corona, 2018). Así, en este trabajo nos centramos en el Indicador Global de la Actividad Económica (IGAE), el cual es una variable proxy mensual del PIB, por lo que resulta relevante tener herramientas econométricas y estadísticas que permitan anticipar el comportamiento de dicha variable.

En Corona et al. (2021) se presenta una metodología para generar estimaciones oportunas del IGAE, la cual consiste en aprovechar el hecho de que actualmente es posible allegarse de grandes volúmenes de información (tradicionales y no tradicionales) que, con una apropiada utilización de técnicas estadísticas y econométricas, pueden dar lugar a generar estimaciones oportunas de la actividad económica de forma oportuna y fiables de manera estadística. En consecuencia, en este trabajo haremos uso de este procedimiento para realizar nowcasts de las tres grandes actividades económicas del IGAE y, también, para algunas componentes de la demanda del PIB, como el Indicador Mensual del Consumo Privado en el Mercado Interior (consumo), la Inversión Fija Bruta en México (inversión) y para las exportaciones e importaciones totales. Lo anterior permitirá a quienes toman decisiones tener una mayor certeza estadística de que es posible realizar estimaciones oportunas para variables relevantes de la coyuntura económica.

El trabajo de Corona et al. (2021) está basado en la estimación de un factor dinámico oportuno y altamente correlacionado con la variable a estimar, el cual se valida tanto en el plano estadístico como en el económico. En particular, se utiliza una serie de técnicas, como: 1) selección de variables no tradicionales a través de regresión LASSO, 2) transformación de variables maximizando la correlación contemporánea con la variable a estimar, 3) estimación de un factor dinámico con la metodología de Doz et al. (2011), 4) utilizar dicho factor en un modelo entrenado de regresión lineal donde también se modela la estructura del error para, finalmente, 5) usar los mejores modelos en datos de prueba para realizar las estimaciones finales. De esta forma, se pueden obtener estimaciones oportunas mensuales y, también, analizar tanto las propiedades estadísticas de los modelos como la estimación de la incertidumbre asociada al factor dinámico, computando los intervalos de confianza del factor y de las contribuciones de este sobre las variables. Los resultados de Corona et al. (2021) se han comparado favorablemente respecto a otros modelos de nowcasting, por ejemplo, el de Statistics Netherlands (Kuiper y Pijpers, 2020), puesto que el intervalo de estimación captura con mayor frecuencia los valores observados en una ventana temporal de 36 periodos.

Si bien las estimaciones oportunas cobran relevancia en el contexto actual, la metodología usada en este trabajo no es de aplicación exclusiva en contextos de alta volatilidad (como el derivado de la pandemia), sino que se puede extender a situaciones de menos inestabilidad, por lo que posteriormente puede seguirse empleando para anticipar los movimientos de las variables macroeconómicas, pues la selección de modelos puede hacerse en diferentes momentos del tiempo que incluyan, o no, el periodo de la pandemia de COVID-19. Por lo anterior, a diferencia por ejemplo de Lenza y Primiceri (2020), donde se reescalan explícitamente las desviaciones en los meses del gran confinamiento, en nuestro caso buscamos que el modelo mismo capture estos movimientos abruptos.

En materia de oportunidad, la metodología empleada permite obtener nowcasts para las variables mencionadas hasta con más de 66 días de anticipación que las estadísticas oficiales. Además, las estimaciones que aquí se presentan captan los choques extremadamente grandes de la economía; por ejemplo, las caídas suscitadas en abril y mayo del 2020 en medio de la emergencia sanitaria por COVID-19. Por lo tanto, los hallazgos son de interés para los académicos, especialistas del sector privado y hacedores de políticas públicas.

Una aportación adicional de este trabajo fue utilizar las estimaciones para realizar análisis de escenarios sobre el posible curso de la economía mexicana en el 2020, que podrían servir para hacer evaluaciones de política económica. Se plantearon dos probables escenarios de corto plazo: en el primero, se asumió que las variables presentarían el mismo comportamiento de acuerdo con su último valor observado y se realizarían las predicciones; lo denominamos un escenario ceteris paribus. El segundo supuso una recuperación en forma de V, asumiendo una mejoría gradual de las variables en diciembre a los mismos niveles de febrero del 2020, es decir, antes del inicio de la pandemia.

El trabajo se estructura de la siguiente forma: en la sección dos se resume la metodología de nowcasting de Corona et al. (2021) y se muestran las fuentes de información; en la tres están las estimaciones para las variables seleccionadas y se discuten dichos resultados; en la cuarta se presentan los posibles escenarios de crecimiento económico de México para el 2020; finalmente, la cinco expone las conclusiones.

 

Metodología

Fuentes de información

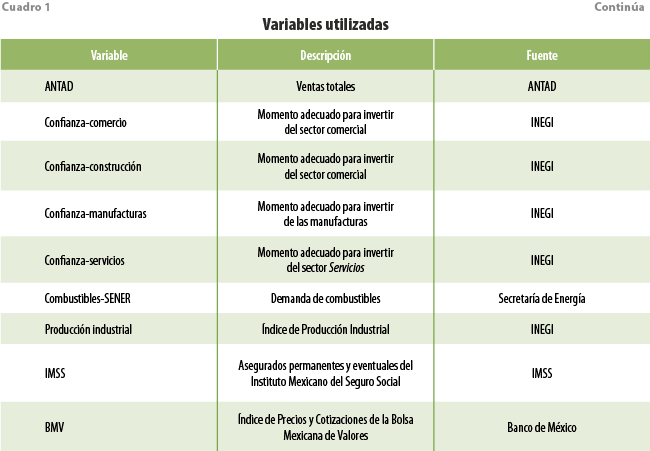
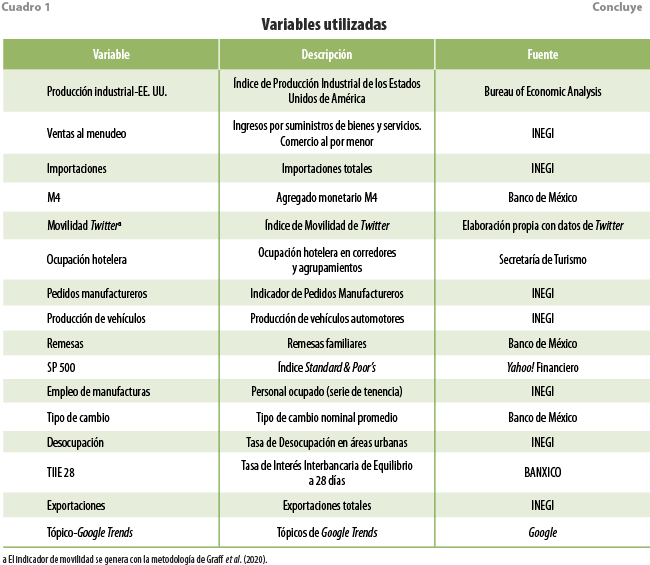
Para cada una de las variables a estimar (ya sea alguna de las tres grandes actividades del IGAE, el consumo, la inversión o las series de comercio exterior), se utiliza inicialmente el mismo conjunto de variables sugeridas por Corona et al. (2021). No obstante, se realizan transformaciones ad hoc a la variable objetivo. Asimismo, se consideran las mismas categorías de información de Google Trends, pero se mantienen solo aquellas que tienen capacidad predictiva sobre la variable de interés. Vale la pena comentar que incluimos al IGAE como variable oportuna para el consumo y la inversión.

Las variables originalmente utilizadas en los modelos de nowcasting se describen en el cuadro 1 y cumplen los criterios de oportunidad y correlación con respecto a la variable de interés; es decir, todas ellas se actualizan al menos antes que la variable que se va a estimar y, además, estas (o alguna transformación de ellas) están correlacionadas con la primera. Todas son de libre acceso y se introducen al modelo con ajuste estacional, ya sea que se publiquen así por la fuente, o bien, se emplea el paquete X-13ARIMA-SEATS para desestacionalizarlas. El conjunto de información comienza su cobertura en enero del 2004 y abarca hasta el último dato disponible para cada variable, es decir, algunas concluyen en mayo, otras en junio y unas más, hasta julio del 2020; en la literatura de series de tiempo esto se conoce como jagged o ragged edge data. Las variables que comprenden la base de datos también han sido utilizadas en la literatura previa, ver por ejemplo a Corona et al. (2017), Caruso (2018) y Gálvez-Soriano (2020).

Oportunidad de las estimaciones 

Para este trabajo, diferenciamos las estimaciones oportunas de las predicciones o pronósticos. En este sentido, los nowcasts se realizan con la información oportuna y de la alta frecuencia que requiere el modelo, es decir, para hacer la estimación de un mes en particular solo consideramos los datos disponibles de otras variables hasta ese mismo mes, mientras que las predicciones o pronósticos se hacen con información para periodos no contemporáneos. Con frecuencia, se suelen explotar las estructuras de dependencias autorregresivas, donde el pasado de la predictora sirve para estimar el futuro de la variable de interés.

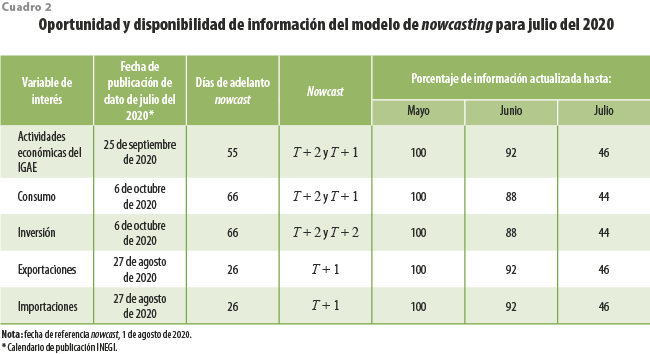
Dada la oportunidad de las cifras oficiales, para las actividades primarias y terciarias, el consumo y la inversión se realizan estimaciones oportunas para T + 1 y T + 2, i.e. para el siguiente mes y dos meses después del último dato oficial publicado (T), mientras que, para las series de actividades secundarias,^[2] exportaciones e importaciones, solo se hacen estimaciones para T + 1. Por ende, dado que las fuentes de información con las cuales se llevan a cabo los nowcasts anteceden a las cifras oficiales, dichas estimaciones se pueden actualizar conforme se incrementa la disponibilidad de datos, y en cada nueva actualización se cuenta con información más completa, lo que reduce aún más el error de estimación. El cuadro 2 muestra la oportunidad de las estimaciones y el porcentaje de datos de que se dispone para las estimaciones de julio del 2020 realizadas el 1 de agosto del mismo año.

 

En general, una vez terminado el mes T se pueden obtener nowcasts para T + 2 con alrededor de 45 % de las variables actualizadas, antecediendo entre 26 y 66 días a las estimaciones oficiales. A su vez, para las que se estiman para T + 1, se cuenta con alrededor de 88 % de las variables actualizadas, con lo que se anticipa entre 25 y 36 días al dato oficial.

 

Transformaciones previas

Si X^* = es es la matriz T × N de variables consideradas para el modelo de factores dinámicos donde cada X_i^*es un vector de dimensión T, se busca una transformación lineal que satisfaga la siguiente condición:

Donde y = (y₁, ..., y_T-H )' es la serie de tiempo a la cual se le realizarán los nowcasts y H es el horizonte de estimación del nowcast, en este caso, 1 o 2 periodos adelante, por lo que estas últimas observaciones, cuando existan, no se consideran para calcular la correlación.

En este caso, las funciones consideradas son: 1) ninguna transformación, 2) cambio porcentual mensual y 3) cambio porcentual anual. Para el caso de las series de Google Trends, se consideran ninguna transformación o el rezago de la variable. Note que estas transformaciones no tienen el objetivo de alcanzar estacionariedad, aunque intrínsecamente son estacionarias, de hecho, las 2 y 3 tienden a serlo cuando las series de tiempo son integradas de orden 1, I(1), lo cual es muy común en las de tipo económicas.

 

Regresión LASSO

La regresión Least Absolute Shrinkage and Selection Operator (LASSO) (Tibshirani, 1996) es una técnica que puede ser utilizada como método de selección de variables cuando se tiene una gran cantidad de estas, dado que las técnicas tradicionales basadas en criterios de información quedan rebasadas al incrementarse exponencialmente la cantidad de covariables. Minimizar la suma de cuadrados residuales, sujeto a que la suma del valor absoluto de los coeficientes sea menor que una constante, permite alcanzar dos objetivos: 1) dejar fuera todas las variables con menor capacidad predictiva y retener aquellas que sí lo son y 2) lograr la regularización de los coeficientes asociados a las variables que permanecen. Este procedimiento se utiliza para seleccionar, dentro de una gran cantidad de tópicos de Google Trends, aquellos que resultan relevantes para la variable objetivo, en un periodo de datos de prueba, por ejemplo, los últimos 36 meses observados. Nótese que los tópicos posibles pueden irse actualizando durante el tiempo y este método de selección incluirá o no aquellos que sean relevantes desde el punto de vista estadístico al momento de realizar la estimación.

 

Modelo de Factores Dinámicos (MFD)

Los MFD fueron originalmente introducidos en economía por Geweke (1977) y Sargent y Sims (1977); se utilizan para condensar la información del conjunto de variables en unos pocos factores con la finalidad de que estos expliquen una parte importante de la variación de los datos. La notación que aquí se sigue puede verse en los estudios de Bai y Ng (2008), Stock y Watson (2011), Breitung y Choi (2013), entre otros.

Formalmente, partimos de un gran número de variables X, que serán utilizadas para pronosticar. Este conjunto contiene N variables con T observaciones cada una. Es posible que N > T. Se busca encontrar un conjunto de variables F y un conjunto de parámetros P que mejor expliquen X.

El MFD puede ser escrito como:

X =FP´ + ε,                              (2)
Φ(L)F = η,                                (3)
Ω (L)ε = a,                                (4)

donde F es la matriz de los r (< N) factores dinámicos; P, la de cargas o las contribuciones de los factores sobre las variables; Φ(L), la que contiene los coeficientes autorregresivos de los factores; y η, la de disturbios del factor. Para la componente idiosincrática (ε), se puede hacer la misma analogía en relación con las matrices Ω(L) y α. Se asume que F puede ser no estacionario, pero ε sí se supone estacionario, restringiendo que las matrices que contienen Φ(L) sean diagonales.

Para estimar F y P se asumen algunas restricciones de identificabilidad (ver Bai y Ng, 2013) de tal forma que  es √N veces los primeros r vectores propios de la matriz X´X, por lo que los factores estimados por componentes principales se determinan como:

Finalmente, se modela la dinámica de ajustando un vector autorregresivo diagonal para obtener las matrices y condiciones iniciales que requiere el filtro de Kalman; de esta manera, utilizando su suavizamiento, se obtiene una versión  que contempla la dinámica temporal del factor, ver por ejemplo Doz et al. (2011, 2012). El uso del suavizamiento de Kalman permite estimar el factor dinámico aun cuando no toda la información esté disponible al tiempo T, de ahí su relevancia en el contexto del nowcasting. El filtro (o suavizamiento) de Kalman puede resumirse como sigue:

1. Estimar los coeficientes Φ(L) por mínimos cuadrados ordinarios, es decir, se modela la dinámica de .
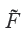2. Usar 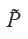 (obtenida por la estimación estática) y las matrices de covarianza de  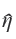y 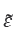 (que se asume diagonal).
3. Generar los valores iniciales para la estimación del factor (generalmente media 0 y varianza obtenida a través de los datos).
4. Usar el suavizamiento de Kalman y cuando X_t sea desconocida, se asume un valor difuso en la diagonal específica de .
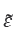5. Finalmente, la expresión de la estimación suavizada es 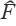= E(F_t |ϒ_t), es decir, la esperanza condicional del factor una vez observada toda la información disponible.

Nótese que  puede considerarse como la contribución de las variables sobre el factor. En este trabajo, la estimación de  se obtiene a través de técnicas Monte Carlo,^[3] tal que se satisface la expresión (5) reemplazando  por  por lo que la contribución de las variables sobre el factor es .

 

Modelo de nowcasting

Una vez que se ha estimado el factor, este se incorpora en el modelo de nowcasting, el cual se especifica de la siguiente manera:

Φ_p (L)u = Θ_q(L)e.                          (6b)

Es decir, se asume una regresión lineal donde el error tiene una estructura autorregresiva y de medias móviles (ARMA), de tal manera que los órdenes p y q se determinan al minimizar el error de predicción en los datos de prueba; en nuestro caso, la media absoluta del error, actualizando los nowcasts un paso hacia adelante. Al modelo de las expresiones (6) puede considerarse regresión con errores ARMA.

Para el número de datos de prueba, usamos la recomendación empírica de Corona et al. (2021), es decir, los últimos 36 meses; lo que cubre un periodo de estabilidad macreoconómica y, también, los meses de la pandemia por COVID-19. La estimación de los parámetros de las expresines (6) se obtiene por máxima verosimilitud. En consecuencia, los nowcasts se realizan como sigue:

Un caso particular, cuando p y q son iguales a 0, es el modelo que proponen Giannone et al. (2008), obra seminal en lo que se refiere a la literatura de nowcasting, mientras que en este trabajo se consideran diferentes combinaciones de p y q y, después, se seleccionan los p* y q* que minimizan el error.

 

Obteniendo los nowcasts

La estrategia empírica para obtener los nowcasts se resume en los siguientes pasos:

1. Seleccionar los tópicos relevantes de Google Trends mediante regresión LASSO. Se considera una ventana de tiempo expansiva (rolling window) para datos de entrenamiento que van desde el inicio de cobertura de la serie hasta T – (36 + i), con i = {1, 2, …, 36}, y se mantienen solo aquellos tópicos cuyos coeficientes estimados sean diferentes de 0 en los últimos tres años; es decir, se realizan 36 estimaciones actualizando un dato nuevo a la vez. Por último, se consideran como tópicos relevantes aquellos que resultaron diferentes de 0 en el percentil mayor a 90 % de las veces.
2. Realizar las transformaciones óptimas para las series de tiempo de acuerdo con la expresión (1).
3. Obtener los valores puntuales e intervalos de confianza para el factor dinámico y las contribuciones del factor sobre las variables del sistema. Se utilizan mil muestras para las estimaciones Monte Carlo de las cargas, una vez que el factor ha sido suavizado por Kalman.
4. Estimar los nowcasts para diferentes valores de p y q y rezagos en el factor dinámico.
5. Seleccionar, de entre todos los modelos de nowcasting, aquellos valores p^* y q^* que minimizan el promedio de las raíces del error cuadrático en los últimos 36 meses. Se utiliza, también, una campana expansiva como datos de entrenamiento para actualizar en cada estimación un nuevo dato.
6. Combinar modelos que, de acuerdo con la prueba de Diebold-Mariano, sean estadísticamente iguales, para lo cual se elige la mediana de las estimaciones realizadas en el paso 4 para los diferentes valores de p y q.
7. Por último, se considera el modelo de Giannone et al. (2008) y se promedian ponderadamente con los nowcasts estimados en el paso 6. Los pesos asignados (w₁), para el modelo de nowcasting y w₂ para el de Giannone et al. (2008),^[4] se obtienen de acuerdo con la ponderación del error en datos de prueba, de tal manera que w₁ + w₂ = 1. Con frecuencia, w₁ > w₂, es decir, el modelo con menor error de predicción suele tener estructura ARMA.

Existen algunas consideraciones metodológicas; por ejemplo, se desea, por interpretabilidad, que el número de factores sea , por lo que se verifica este supuesto con el criterio de Onatski (2010). También, se confirma que los errores idiosincráticos sean estacionarios con la prueba PANIC (Bai y Ng, 2004), de tal forma que se garantiza la consistencia estadística de la estimación de la componente común. Por último, se realiza la prueba Ljung-Box para corroborar que los errores del modelo de nowcasting (û) no estén autocorrelacionados.

 

Resultados

Nowcasts para variables relevantes de la coyuntura económica de México

El corte de actualización de las fuentes de información se hizo al 13 de agosto de 2020. De esta manera, las estimaciones a realizarse serán para los meses de junio y julio del 2020 para las componentes del IGAE, el consumo y la inversión, mientras que, para las exportaciones e importaciones totales, ya se tienen cifras oficialmente publicadas para junio; es decir, en estos casos solo se realizarán los nowcasts para julio del 2020. Las variables por estimarse están expresadas como variaciones porcentuales anuales.

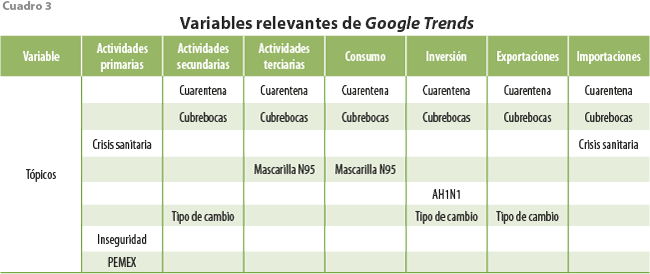
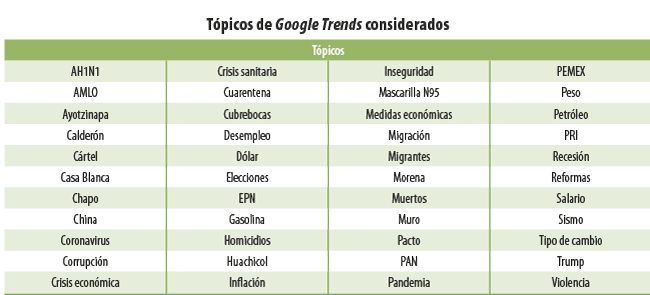
A partir del conjunto de tópicos de Google Trends considerados (ver Anexo), la metodología LASSO nos permite identificar solo aquellos que resultan relevantes para cada una de las variables, los cuales se detallan en el cuadro 3.

 

De los 44 tópicos considerados, para cada variable solamente resultan significativos entre dos y cuatro de ellos. De hecho, en conjunto, solo hay nueve categorías relevantes, ya que algunos son comunes entre las diferentes variables; por ejemplo, en todas se encuentra, al menos, un tópico relacionado con la pandemia de COVID-19 (cuarentena, cubrebocas, mascarilla N95 y crisis sanitaria). Otro tópico que llama la atención es el de tipo de cambio, que es relevante para las variables de actividades secundarias, inversión y exportaciones. También, llama la atención cómo, para las actividades primarias, además de tener relación con el tópico crisis sanitaria, estas tienen relación con búsquedas de internet en otros temas, como inseguridad y PEMEX (ver cuadro 3).

Con ello, puede considerarse que la información de Google Trends refleja oportunamente el rumbo de la economía en el muy corto plazo y que la herramienta LASSO brinda flexibilidad al modelo para que las variables que se introducen en un nuevo nowcast se actualicen con aquellas que mejor reflejen las circunstancias actuales. No obstante, el conjunto de tópicos seleccionados en este ejercicio es estático y, por el momento, está sujeto al criterio del investigador, por lo que al cambiar las condiciones del contexto del momento se requiere actualizar este grupo de palabras, por ejemplo, en caso del surgimiento de desastres naturales catastróficos, como terremotos, huracanes o inundaciones, entre otros. Así, cobra relevancia el rol de la información alternativa a los indicadores económicos tradicionales y, más aún, el uso de métodos estadísticos apropiados que sustenten su incorporación al modelo de nowcasting conforme cambien las condiciones socioeconómicas. Si bien el procedimiento estadístico es consistente, las variables que se incorporan a los modelos podrían variar entre periodos, lo que podría limitar comparaciones entre ellos.

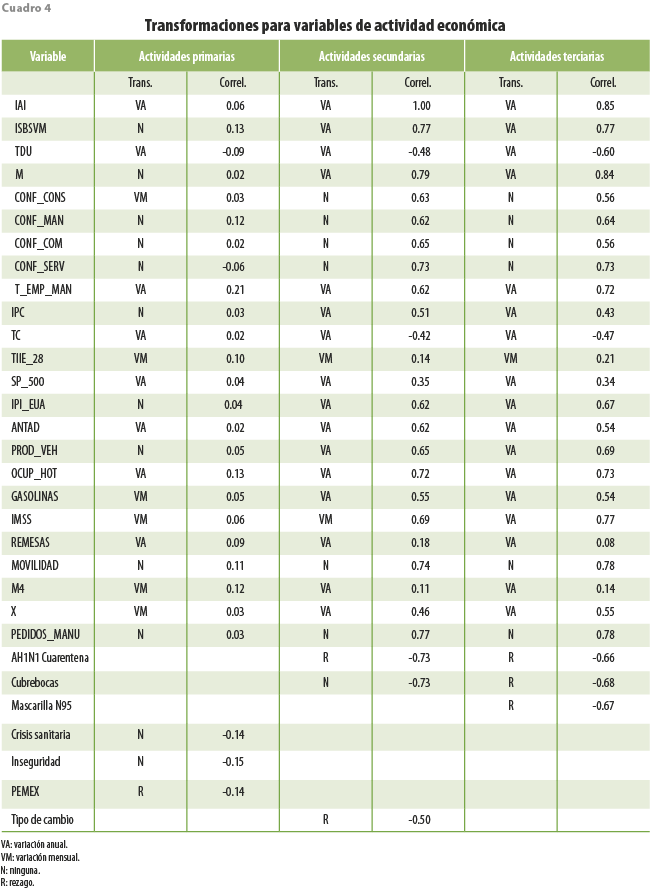
Las transformaciones realizadas para cada conjunto de datos, de acuerdo con cada una de las variables de actividad económica, se describen en el cuadro 4.

 

Es de llamar la atención cómo para las actividades primarias las variables están levemente correlacionadas, no así para las otras dos grandes actividades económicas. El cálculo de las dependencias efectivas muestrales por sector de actividad es de 0.64, 0.81 y 0.79 para las actividades primarias, secundarias y terciarias, respectivamente; es decir, se encuentran dependencias más altas en las secundarias. Además, se puede ver que las transformaciones que dominan son las variaciones anuales (VA), principalmente porque las variables objetivo están expresadas de esa forma. Es interesante ver que las variables de opinión empresarial (CONF_CONS, CONF_MAN, CONF_COM y CON_SERV) y el indicador de movilidad, la transformación óptima es ninguna (N), que puede ser por la naturaleza estacionaria de los indicadores, mientras que para los tópicos de Google Trends, la transformación más común es el rezago (R); es decir, los agentes económicos reaccionan con mayor prontitud que la economía.

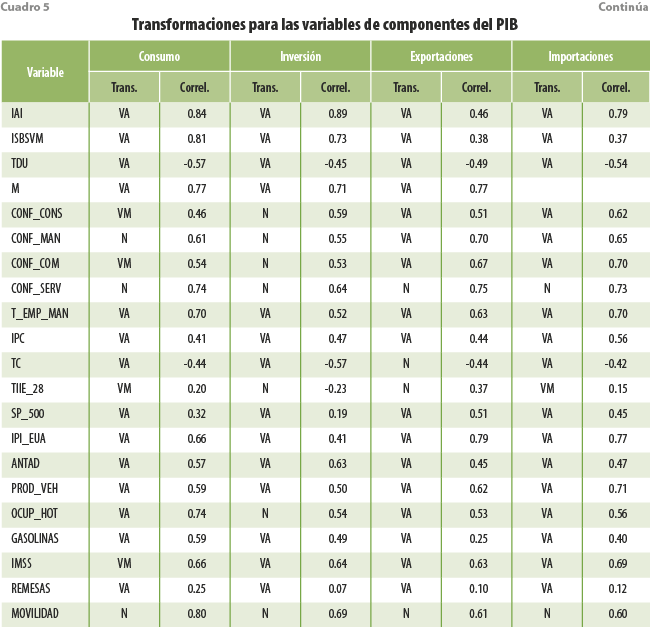
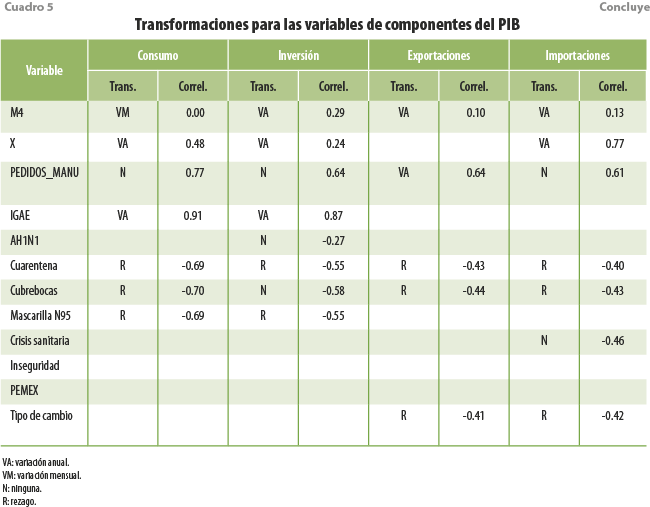
De manera similar, el cuadro 5 detalla los resultados de las transformaciones previas y sus correlaciones con respecto a las componentes del PIB.

 

Para las componentes del PIB, podemos apreciar correlaciones altas, con dependencias efectivas muestrales de 0.76, 0.79, 0.75 y 0.73, respectivamente, dominando también las variaciones porcentuales anuales como tipo de transformación. A diferencia de las variables de actividad económica, las transformaciones óptimas para las variables de opinión empresarial varían según el tipo de variable, aunque también, los tópicos de Google Trends suelen expresarse en rezagos.

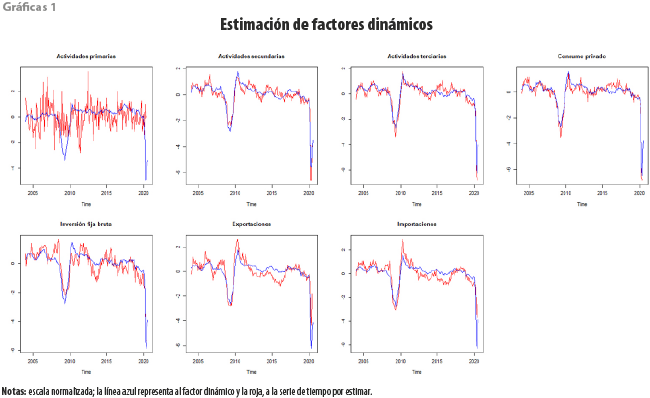
Las gráficas 1 resumen las estimaciones del factor dinámico para cada una de las variables.

 

Se puede apreciar que, en todos los casos, se estima un factor altamente correlacionado con la variable de interés, con excepción de las actividades primarias; de esta forma, los nowcasts para esta variable pueden ser no confiables. Las correlaciones contemporáneas entre el factor y las variables son 0.14, 0.95, 0.95, 0.94, 0.85, 0.83 y 0.82 para las actividades primarias, secundarias y terciarias; consumo; inversión; exportaciones e importaciones totales, respectivamente. Esto corrobora la esencia del ejercicio, que es generar un factor dinámico altamente correlacionado con la variable de interés, situación conseguida sobre todo para los sectores industrial y de servicios, además del consumo; medianamente para la inversión, las exportaciones e importaciones; y, de forma muy débil, para las actividades primarias. Claro está, este sector se relaciona con otra dinámica, quizá algunas de ellas más de carácter climático o factores intrínsecos a la producción y el abastecimiento de recursos. Los intervalos de confianza del factor estático no se presentan en este trabajo, pero están disponibles bajo petición.

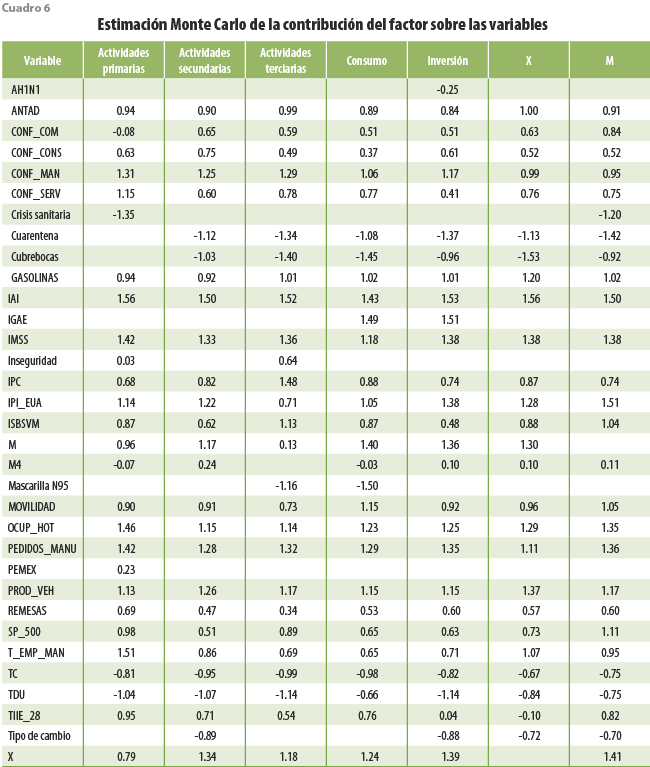
Las contribuciones del factor (loadings) sobre las variables, que también pueden interpretarse como coeficientes estandarizados de la regresión, están denotadas por (ver cuadro 6).

 

Se puede apreciar que las variables tienen signos esperados de acuerdo con la teoría económica; por ejemplo, la tasa de desocupación y el tipo de cambio tienen un rol inverso en el factor. Recordando la expresión (5), podemos interpretar al factor como una función de las variables, lo cual quiere decir que estas contribuyen de manera inversa en el factor, mientras que el resto lo hace de manera directa. Los intervalos de estimación no se presentan para ahorrar espacio, pero se pudo constatar que todas las variables son significativas a 95 % de confianza. Los resultados completos están disponibles bajo petición.

Una vez estimados los factores y las cargas asociadas a las variables, se realizan los nowcasts para cada una de las variables consideradas junto con sus intervalos de confianza. En el cuadro 7 se muestran los resultados de los nowcasts para la actividad económica con sus respectivos intervalos de confianza a 95 por ciento.

 

En este sentido, se estiman variaciones del IGAE con respecto al mismo mes del año anterior de -15.2 % para junio y -13.2 % para julio del 2020. Considerando las grandes actividades del IGAE se tiene que, para las actividades primarias, se esperan crecimientos anuales de 3.4 % en junio y 0.3 % en julio. En cuanto a las secundarias, se estiman caídas anuales de -15.7 % para julio. Finalmente, para las terciarias, las variaciones esperadas son -12.9 y -10.7 % para junio y julio del 2020, respectivamente.

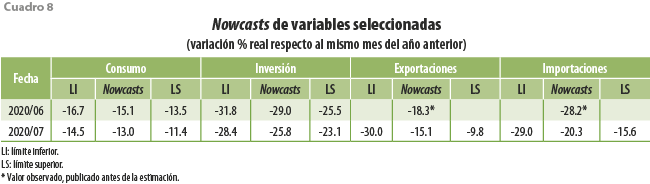
En el cuadro 8 se presentan los resultados de las estimaciones para el consumo, la inversión, las exportaciones y las importaciones totales.

 

Para el consumo, se estima que las variaciones anuales de junio y julio son -15.1 y -13.0 %, respectivamente; para la inversión, se prevén de -29.0 % en junio y -25.8 % en julio. En cuanto a exportaciones e importaciones, se calculan caídas anuales de -15.1 y -20.3 % para julio. Cabe aclarar que, para las variaciones porcentuales anuales de las exportaciones e importaciones totales de junio del 2020, los datos reportados en el cuadro corresponden a las cifras oficiales previamente dadas a conocer por el INEGI.

 

Pruebas de validación

De acuerdo con Corona et al. (2021), el modelo de nowcasting que aquí se presenta genera una mediana del error absoluto (MEA) de 0.65 y los intervalos de confianza capturan a la variable en 92 % de los casos para el IGAE. Además, ahí se pueden ver, también, las correlaciones del factor estimado a lo largo del tiempo, las cuales son más altas en periodos de incertidumbre (0.98) y, en contexto de menos volatilidad, disminuye ligeramente la correlación hasta 0.95 en el 2016. También, para verificar la utilidad de incluir las variables no tradicionales, en Corona et al. (2020) se realiza una comparación del MEA entre tres modelos: el DFM que aquí se presenta, uno DFM pero que asigna pesos iguales dentro del factor y otro DFM sin la información de Google Trends y la variable de movilidad. Se obtiene que el MEA para estos tres modelos es de 0.65, 1.02 y 0.74, respectivamente, lo que corrobora la utilidad tanto del modelo actual como de la información de Google Trends.

 

Comentarios sobre el error de estimación

Al momento de realizar las estimaciones aquí mostradas (13 de agosto de 2020) no se contaba aún con los datos del IGAE para junio, los cuales fueron publicados el 25 de agosto, lo cual permite comparar los nowcast con respecto a las cifras observadas. Así, las variaciones porcentuales anuales observadas en junio fueron -1.5 y -13.6 % para las actividades primarias y terciarias, respectivamente, mientras que las estimaciones para julio fueron 3.4 y -12.9 por ciento. Se puede observar que la estimación fue fiable para las actividades terciarias; en cuanto a las primarias, se observa que la estimación es poco certera dada la poca relación que se tiene con el factor dinámico (ver gráficas 1). Nótese que no se hace comparación para las actividades secundarias de dicho mes, ya que el dato de la actividad industrial (IAI) se puede considerar prácticamente un reflejo de la componente de actividades secundarias en el IGAE. 

Para las exportaciones de julio, el dato observado (publicado el 27 de agosto) fue de -8.8 % y para las importaciones, de -26.3 %, mientras que sus nowcasts respectivos fueron de -15.1 y -20.3 por ciento. Nótese que, para el caso de las exportaciones, aunque se capta la caída, esta no cubre el intervalo superior, no así para las importaciones, siendo la desviación respecto al real de 6 por ciento. Estos resultados llevan a plantear que el modelo de nowcasting es más certero para estimar la actividad económica, que es la naturaleza propia de estos modelos, que para las componentes del PIB donde, incluso, podemos ver que los intervalos de confianza son más amplios.

Para el consumo y la inversión no se puede hacer una comparación en este sentido dado que, a la fecha de escribir estas líneas, no había cifras oficiales publicadas con las cuales hacer la comparación.

 

Escenarios económicos de corto plazo

Para ilustrar la utilidad de la metodología empleada en este trabajo, en esta sección presentamos dos entornos de crecimiento económico para lo que resta del 2020. En el primero, realizamos los nowcasts del IGAE (o, en este caso, predicciones), asumiendo que las variables del MFD tendrían los mismos valores hasta dicha fecha, según su última observación, denominado ceteris paribus. En el segundo, al que llamamos V, asumimos que las variables recuperarían para diciembre los mismos niveles de febrero. La selección de los escenarios como se presentan obedece a que, al ser opuestos entre sí, nos permitiría imaginar un continuo de posibles perspectivas, entre los cuales se vislumbraría la economía mexicana hasta diciembre del 2020. Uno de particular interés es el punto medio de ellos, el cual se presenta al final de este apartado. 

Escenario ceteris paribus

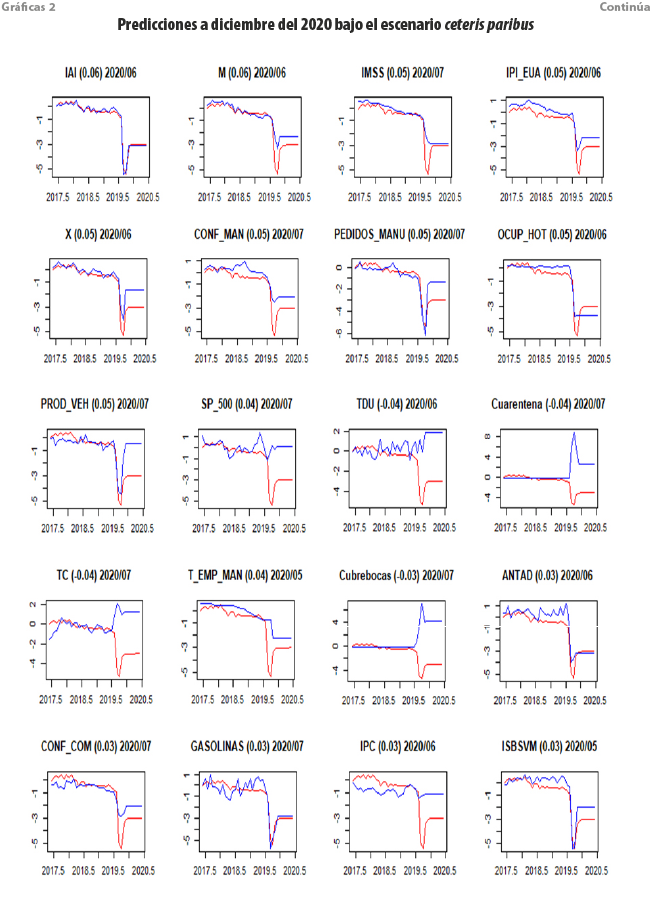
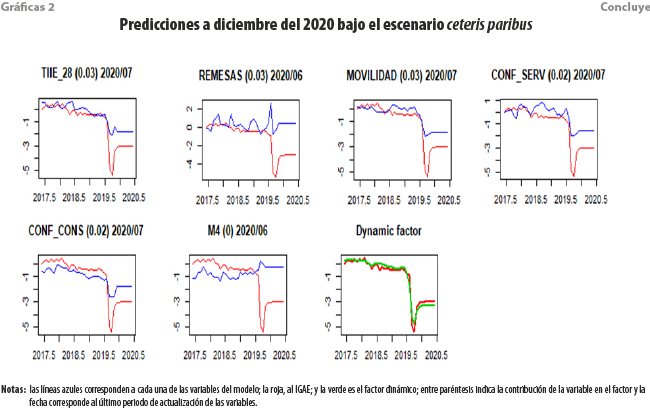
Este asume que para cada una de las variables que integran al MFD, sus valores a diciembre del 2020 son los mismos que el último observado, con lo cual se anticipa que la situación económica al final del año sería muy similar a la que ocurrió en mayo, junio y julio del 2020. Las gráficas 2 muestran los resultados esperados bajo este escenario.

 

Se puede apreciar que, si las variables del MFD mantienen los mismos niveles de crecimiento, los incrementos estimados rondan sobre el último nowcast realizado, es decir, julio del 2020, calculando valores alrededor de -13.5 % y, puntualmente, para diciembre del 2020, una caída de -13.8 por ciento. Anualizando los resultados, el escenario de crecimiento económico para México en el 2020 genera un intervalo a 95 % de -12.7, -12.2, -11.7, es decir, se esperaría un decremento alrededor de -12.2 por ciento.

Escenario V

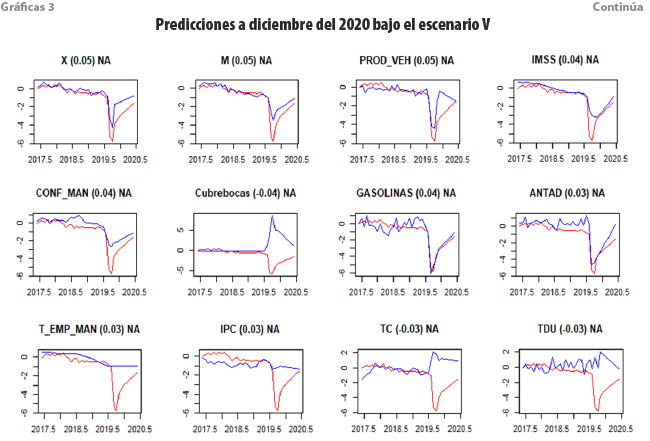
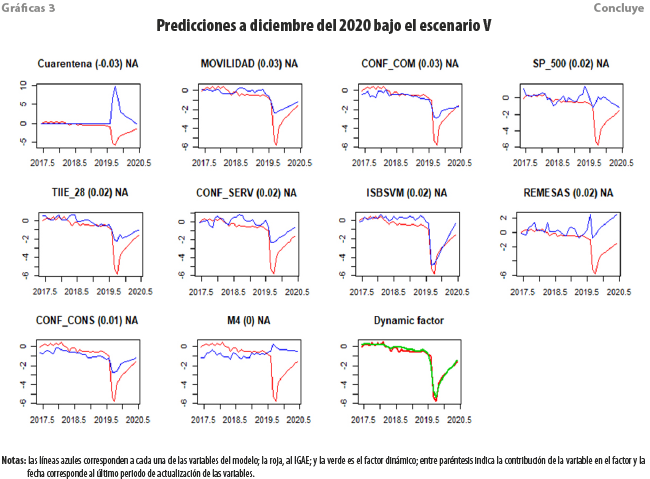
Considera una recuperación en forma de V, es decir, asume una mejoría gradual de la economía reflejada, donde las variables del MFD regresan a su valor prepandemia para diciembre del 2020 (ver gráficas 3).

 

 

Nótese cómo, en este escenario, las series de tiempo se recuperan en forma de V, llegando a los niveles que se habían suscitado con anterioridad, específicamente, a febrero del 2020. Si ocurriese esto, las tasas de crecimiento esperadas son de -15.7 % en junio del 2020 a -4.4 % en diciembre del mismo año, lo que genera un intervalo a 95 % anualizado al 2020 de -9.2, -8.8, -8.3, es decir, un decremento alrededor de -8.8 por ciento.

Considerando ambos escenarios como igualmente probables y calculando el promedio de ambos intervalos de confianza nos genera un nuevo intervalo de -11, 10.5, -10, es decir, el crecimiento esperado de México al 2020 estaría alrededor de -10.5 por ciento.

Conclusiones

Siguiendo a Corona et al. (2021), en este trabajo se generan nowcasts o estimaciones oportunas durante el periodo junio y julio del 2020 para variables relevantes de la economía mexicana, como las tres grandes actividades económicas del IGAE y algunas componentes del PIB, en particular el consumo, la inversión, las exportaciones e importaciones totales. La principal característica de estas es su oportunidad, ya que se anticipan hasta 66 días a la publicación del dato oficial. Esta metodología nos permite, también, hacer análisis de política económica, para lo cual se consideraron dos escenarios extremos para la economía mexicana en lo que restaba del 2020.

La principal aportación de esta investigación consiste en validar y brindar certeza al funcionamiento de la metodología propuesta al abarcar una mayor cantidad de series de tiempo y no solo enfocarnos a agregados. Se encontró que las estimaciones son más cercanas a las observadas para el sector terciario, el consumo y la inversión, mientras que para las exportaciones e importaciones, los resultados de las primeras no caen en el intervalo estimado, pero sí para las segundas, aunque este es relativamente amplio. De esta forma, se concluye que para estas dos variables es necesario generar modelos con variables específicas que capturen de mejor manera sus dinámicas particulares.

En lo que respecta a los escenarios de crecimiento económico para el 2020, el ceteris paribus indica que se esperaría, en promedio, una tasa de crecimiento anual de -12.2 %, mientras que el de forma en V indica una tasa de crecimiento anual de -8.8 por ciento. Promediando ambos, el resultado muestra que la tasa de crecimiento anual del 2020 rondaría en -10.5 por ciento.

Como futura línea de estudio, se considera conveniente incorporar más series de tiempo relacionadas con el sector externo, similar a lo que propone Caruso (2018) o, en su caso, otra metodología en específico. Una aportación importante es que las estimaciones derivadas de los modelos de nowcasts pueden combinarse para formular posibles escenarios para la recuperación de la economía mexicana, de las cuales se eligen dos, que posteriormente se combinan, y se concluye que, si los asumimos como igual de probables, la tasa de crecimiento económica esperada para el 2020 sería de -10.5 por ciento. Otra línea de investigación abierta es analizar la conveniencia de incorporar una metodología que permita incorporar tópicos relevantes de Google Trends de manera dinámica, que capturen la coyuntura del acontecer socioeconómico de México, para lo cual son relevantes herramientas de procesamiento de lenguaje natural.

 

Fuentes

Bai, J. & S. Ng. Large dimensional factor analysis. Now Publishers Inc., 2008.

_______ “A panic attack on unit roots and cointegration”, en: Econometrica. 72(4). 2004, pp. 1127-1177.

_______ “Principal components estimation and identification of static factors”, en: Journal of Econometrics. 176(1). 2013, pp. 18-29.

Breitung, J. e I. Choi. “Factor models”, en: Hashimzade, N. y M. Thorthon (eds.). Handbook of research methods and applications in empirical macroeconomics. Cheltenham, Edward Elgar, 2013, pp 249-265.

Caruso, Alberto. “Nowcasting with the help of foreign indicators: The case of Mexico”, en: Economic Modelling. 69. 2018, pp. 160-168.

Corona, Francisco, G. González-Farías y J. López-Pérez. A nowcasting approach to generate timely estimates of Mexican economic activity: An application to the period of COVID-19. 2021. arXiv:2101.10383 [stat.AP].

Corona, Francisco, Graciela González-Farías y Pedro Orraca. “A dynamic factor model for the Mexican economy: are common trends useful when predicting economic activity?”, en: Latin American Economic Review. 26(1). 2017, pp. 1-35.

Delajara, Marcelo, Federico Hernández y Abel Rodríguez. “Nowcasting Mexico’s Short-Term GDP Growth in Real-Time: A Factor Model versus Professional Forecasters”, en: Economia. 17(1). 2016, pp. 167-182.

Doz, C., D. Giannone y L. Reichlin. “A two step estimator for large approximate dynamic factor models”, en: Journal of Econometrics. 164(1). 2011, pp. 188-205.

_______ “A quasi maximum likelihood approach for large, approximate dynamic factor models”, en: The Review of Economics and Statistics. 94(4). 2012, pp. 1014-1024.

_______ “A two-step estimator for large approximate dynamic factor models based on Kalman filtering”, en: Journal of Econometrics. 164(1). 2011, pp. 188-205.

Galvez-Soriano, Oscar de Jesús. “Nowcasting Mexico's quarterly GDP using factor models and bridge equations”, en: Estudios Económicos. 35(2). 2020, pp. 213-265.

Geweke, J. “The dynamic factor analysis of economic time series”, en: Aigner, D. J. y A. S. Goldberger (eds.). Latent variables in socio-economic models. North-Holland, Amsterdam, 1977.

Giannone, Domenico, Lucrezia Reichlin y David Small. “Nowcasting: The real-time informational content of macroeconomic data”, en: Journal of Monetary Economics. 55(4). 2008, pp. 665-676.

Graff, M., D. Moctezuma, S. Miranda-Jiménez y E. S. Téllez. A Python Library for Exploratory Data Analysis and Knowledge Discovery on Twitter Data. Working paper. 2020 (DE) https://bit.ly/3niDsvN

Guerrero Víctor M. y F. Corona. “Retropolación hasta 1980 de algunas series del Sistema de Cuentas Nacionales de México”, en: Realidad, Datos y Espacio Revista Internacional de Estadística. 9(3). 2018, pp. 98-119.

Kuiper, M. & F. P. Pijpers. Nowcasting GDP growth rate: a potential substitute for the current flash estimate. Reporte técnico. Statistics Netherlands. Mayo del 2020.

Lenza, M. y G. E. Primiceri. How to Estimate a VAR after March 2020. Technical report. National Bureau of Economic Research, 2020.

Onatski, Alexei. “Determining the number of factors from empirical distribution of eigenvalues”, en: The Review of Economics and Statistics. 92(4). 2010, pp. 1004-1016.

Sargent, T. J. y C. A. Sims. “Business cycle modeling without pretending to have too much a priory economic theory”, en: Sims, C. A. (ed.). New methods in business cycle research Minneapolis. Minneapolis, Federal Reserve Bank of Minneapolis, 1977.

Stock, J. y M. Watson. M. “Dynamic factor models”. en: Clements, M. y D. Hendry (eds.). Oxford handbook of economic forecasting. Oxford, Oxford University Press, 2011.

Tibshirani, Robert. “Regression shrinkage and selection via the LASSO”, en: Journal of the Royal Statistical Society. Series B (Methodological). 58(1). 1996, pp. 267-288.

 

 

 

^[1] Mediana de crecimiento tomada de la Encuesta sobre las Expectativas de los Especialistas en Economía del Sector Privado. Banco de México, julio del 2020.

^[2] Se considera como observado el dato del Índice de Producción Industrial publicado oficialmente sobre el día 10 de cada mes, que representa alrededor de 97 % del total de las actividades secundarias, publicadas de manera oficial sobre el 25 de cada mes (Metodología IMAI).

^[3] Se hacen mil simulaciones suponiendo una distribución uniforme con parámetros [a, b], donde a y b son los límites inferior y superior del intervalo de confianza obtenido para la carga de cada variable.

^[4] Empíricamente se pudo verificar que combinar estos modelos genera ganancias en el error en el cambio de la variación porcentual anual del IGAE al representar la dinámica pura de las variables que integran al MFD. Se presume que esta misma ganancia continúa para las variables estimadas en este trabajo.