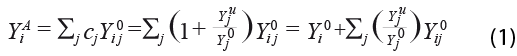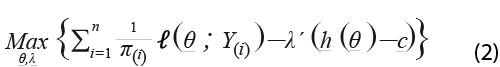Seguimiento de la distribución del ingreso en México a lo largo del tiempo y de la geografía

 

Monitoring the Income Distribution in Mexico over Time and Geography

 

*Instituto Nacional de Estadística y Geografía (INEGI), alfredo.bustos@inegi.org.mx y miriam.romo@inegi.org.mx, respectivamente.

Nota: las opiniones contenidas en esta investigación son responsabilidad exclusiva de sus autores y pueden no coincidir con las de su institución de adscripción, el INEGI; se agradecen las aportaciones de árbitros anónimos que han contribuido a mejorar el presente trabajo; los errores que permanezcan son total responsabilidad de quienes lo desarrollaron.

Vol. 13, núm. 3 –  EPUB                                Seguimiento de la distribución… – EPUB 

Este trabajo discute la evolución de la distribución del ingreso en México para el 2010, 2012, 2014 y 2016. Adicionalmente, se hace una desagregación geográfica al nivel estatal para los mismos años. El análisis se basa, principalmente, en mediciones de desigualdad derivadas de estimaciones para dichas distribuciones y su comparación tanto entre sí como con mediciones semejantes derivadas de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH) o su Módulo de Condiciones Socioeconómicas del Instituto Nacional de Estadística y Geografía. Las estimaciones son obtenidas aplicando el criterio de máxima pseudo-verosimilitud restringida (MPVR) en un afán de hacer uso simultáneo de varias fuentes de datos para mejorar la estimación de la distribución del ingreso. Nos proponemos establecer nuevas comparaciones con los resultados muestrales para ratificar o rectificar el comportamiento de diversas tendencias aparentes durante el periodo. Mostraremos que los ajustes realizados dan lugar a una tendencia creciente en el Gini a nivel nacional, lo que contrasta con el decremento en el valor del mismo indicador para la ENIGH. En otras palabras, nuestros resultados indican que, durante el periodo, la desigualdad se incrementó. La que se presenta al interior de las entidades federativas parece en cambio no haber experimentado una evolución significativa. Lo anterior parece sugerir que lo que ha impulsado el crecimiento de la desigualdad en el país es el aumento de esta entre los estados. Palabras clave: ingreso; máxima pseudo-verosimilitud restringida (MPVR); desigualdad.

This paper discusses the evolution of income distribution in Mexico for 2010, 2012, 2014 and 2016. Additionally, a geographic disaggregation is made at the state level for the same years. The analysis is mainly based on inequality measurements derived from estimates for these distributions and their comparison both with each other and with similar measurements derived from the National Household Income and Expenditure Survey (ENIGH) or its Socioeconomic Conditions Module of the National Institute of Statistics and Geography (INEGI). The estimates are obtained by applying the restricted maximum pseudo-likelihood criterion (MPVR) in an effort to make simultaneous use of several data sources to improve the estimation of income distribution. We propose to establish new comparisons with the sample results to ratify or rectify the behavior of various apparent trends during the period. We will show that the adjustments made give rise to an increasing trend in the Gini at the national level, which contrasts with the decrease in the value of the same indicator for the ENIGH. In other words, our results indicate that, during the period, inequality increased. On the other hand, inequality within states does not seem to have evolved significantly. This seems to suggest that what has driven the growth of inequality in the country is the increase in inequality between states. Key words: income; maximum constrained pseudo-likelihood (MCPL); inequality.

Recibido: 8 de octubre 2020
Aceptado: 10 de diciembre de 2021

 

Introducción

Las fuentes de información estadística sobre el ingreso de los hogares son diversas. Todas ellas muestran ventajas y desventajas en cuanto a la estimación de la distribución del ingreso.^[1] Sin duda, la mejor conocida es la representada por los censos de población y vivienda, que son levantados con diversas frecuencias, usando distintas metodologías, por casi todos los países del planeta. Su cobertura universal da lugar a un alto costo de recolección y, en consecuencia, a un intervalo que comprende varios años entre un levantamiento y el siguiente. Dicha cobertura lleva habitualmente a pensar que la información recolectada durante esos ejercicios es más precisa. Sin embargo, ello es más o menos cierto dependiendo del tema o de la variable de que se trate. En el caso particular del ingreso se presentan limitaciones que han llevado a la División de Estadística de la Organización de las Naciones Unidas a excluirla del grupo de variables censales importantes a ser recolectadas (ver DESA, 2017, tabla 3). Por principio de cuentas, no es del todo claro que la persona que proporciona los datos conozca con precisión los ingresos de cada uno de los perceptores en la vivienda, o sus fuentes. Tampoco es claro si la declaración se refiere a ingresos brutos o netos, pues no es fácil que conozca las deducciones experimentadas por los ingresos por trabajo, sean estas fiscales, de seguridad social o de alguna otra naturaleza. Lo anterior es agravado cuando la declaración del monto del ingreso es falseada o de plano omitida, por ejemplo, bajo circunstancias de alta inseguridad.

La recolección de información que se lleva a cabo a través de encuestas no especializadas en la medición del ingreso de los hogares enfrenta limitaciones similares a las censales. Una excepción a lo anterior la representa el caso de aquellas para las que una de cuyas temáticas principales es el estudio del ingreso de los hogares.^[2] En ellas se busca, por lo general, que cada uno de los perceptores aporte datos acerca de su propio ingreso. Adicionalmente, para cada uno de ellos, se indaga sobre el ingreso percibido por distintas fuentes, entre las que se encuentran las provenientes de un trabajo, ya sea dependiente de terceros o no, las transferencias gubernamentales o de parientes, así como los apoyos y préstamos de familiares o amigos, por mencionar algunas de ellas. En otras palabras, se contempla un mayor desglose temático a costa de uno geográfico menor. Además de esta desventaja, otras limitaciones de este enfoque se refieren a la representatividad de la muestra, pregunta importante en la producción de estadística oficial. En general, es muy difícil que la pequeñísima fracción de la población cuyos ingresos son extraordinariamente altos esté representada en una muestra aleatoria. Dado su pequeño tamaño, puede pensarse que es despreciable el error cometido al considerar que esta sí representa a la población, pero cuando se considera el tamaño extraordinario de sus ingresos dicha idea debe ser revisada. Asimismo, como en el caso censal, tampoco es claro si el monto del ingreso es subdeclarado cuando no, de plano, omitido.

Una fuente que podría representar una cobertura universal en relación con los ingresos está constituida por los registros fiscales. En teoría, cada uno de los perceptores reportaría de manera periódica, por lo menos una vez cada año, a la autoridad hacendaria tanto el monto de sus ingresos como las aportaciones fiscales realizadas en un periodo determinado. En adición a la declaración del total percibido, las declaraciones fiscales por lo general permiten hacer referencia a cada una de las fuentes que componen dicho ingreso. Sin embargo, con frecuencia, los registros administrativos nacen con la intención de atender necesidades específicas, sin tomar en cuenta usos estadísticos alternativos que es deseable dar a la información. Por supuesto, los fiscales no son la excepción. En general, no cumplen con la cobertura universal por diversas razones, entre las que destaca la situación de informalidad laboral en la que se desempeña una fracción más o menos importante de la población económicamente activa; asimismo, no todos los trabajadores formales están obligados a presentar una declaración anual. Por lo anterior, el registro que recoge las declaraciones fiscales anuales de las personas físicas solo se refiere a aquella parte de la población que, o bien está obligada a presentarla por satisfacer una o más condiciones reglamentarias, o que lo hace voluntariamente para obtener una devolución parcial de impuestos. Un registro fiscal complementario es aquel que concentra los reportes patronales sobre los pagos de sueldos y salarios a sus trabajadores, así como sobre las retenciones fiscales o de otra naturaleza que les realizan. Esta información se actualiza mes con mes, pero debe enfatizarse que cubre solo a los empleados formales.

A su vez, el Sistema de Cuentas Nacionales (SCN) representa un esfuerzo internacional por hacer disponibles grandes resúmenes que reflejen la situación económica de los países. Entre sus mayores virtudes está la de basarse en una metodología coherente que les otorga gran consistencia y que está en constante actualización para adaptarse a nuevas circunstancias (INEGI, 2017). Las cuentas nacionales proporcionan una descripción integral de toda la actividad económica de una nación, incluyendo aquellas que involucran unidades domésticas (es decir, los individuos y las entidades residentes en el territorio) y las externas (los residentes en otros países).

Existen dos grandes tipos de sectores institucionales.^[3] De un lado se encuentran las entidades jurídicas o sociales reconocidas por ley que llevan a cabo actividades y operaciones en nombre propio, como las empresas, unidades gubernamentales e instituciones sin fines de lucro que sirven a los hogares, para las cuales se posee un conjunto completo de cuentas y balances de activos y pasivos. El otro reúne a las personas y a los hogares o grupos de individuos, así como a las empresas individuales sin personalidad jurídica, que pueden ser propietarios de activos y contraer pasivos, pero no tienen obligación legal de contabilizar sus actividades. Para fines de la determinación de la distribución del ingreso, el SCN solo aporta agregados a nivel nacional y, en algunos casos, al estatal. Sabemos que se realizan esfuerzos por lograr lo que se denomina Cuentas Nacionales Distributivas^[4] (DINA, por sus siglas en inglés). Dichos esfuerzos destacadamente hacen uso de series de datos fiscales y de cuentas nacionales armonizados, complementadas con encuestas de ingresos y de riqueza, así como con datos de pago de impuestos por herencias y propiedades.

 

Inconsistencia entre los agregados muestrales y los de la contabilidad nacional

La estimación del ingreso corriente total (ICT) de los hogares aportada por las encuestas en diversas naciones muestra una discrepancia más o menos importante con el total determinado por los SCN para el sector institucional de hogares. En el caso mexicano, la información muestral estima un total para el ingreso corriente de estos que alcanza consistentemente un valor menor a la mitad del que consigna el Sistema de Cuentas Nacionales de México (SCNM). Ha sido usual, en este como en muchos otros países, asignar mayor credibilidad a esta última cifra. En consecuencia, se ha buscado determinar las causas que dan lugar a la aparente subestimación. Hoy en día se identifican dos principales, ya mencionadas, e identificadas como subdeclaración y truncamiento.

Leyva-Parra (2004) analiza diversas propuestas cuyo fin es el de reducir la discrepancia mencionada, desde Martínez (1970) hasta el 2004, sobre el ajuste de los ingresos de los hogares obtenidos de encuestas especializadas a resultados provenientes del SCNM para, de esta manera, hacer explícitos los supuestos de los que depende la validez de tales ajustes y, con ello, mostrar las limitaciones de los procedimientos analizados. De paso, cuestiona la validez de las cifras provenientes del SCNM como referente para la corrección de los datos de las encuestas de ingresos de los hogares.

De acuerdo con Leyva, la experiencia mexicana en cuanto al “… ajuste a Cuentas Nacionales, ya sea por niveles, fuentes o alguna combinación de ambos, descansa en los siguientes supuestos básicos:

1. Los conceptos de ingresos manejados en ambas fuentes son equiparables.
2. Los ingresos captados en las Cuentas Nacionales son al menos tan verosímiles como los de las encuestas de ingresos de los hogares.
3. Las diferencias entre ambas fuentes se deben fundamentalmente a problemas de subreporte y no a problemas de truncamiento.
4. Existe una regla de asignación óptima que permite distribuir el ingreso de los hogares, a nivel macroeconómico, al ingreso (expandido) de cada uno de los hogares en la muestra de la encuesta de ingresos (nivel microeconómico). Es una regla óptima en el sentido de que maximiza la verosimilitud de la distribución del ingreso resultante…”.

Desde luego, algunos de los anteriores supuestos son más sensatos que otros, en tanto que los de un tercer grupo no se sostienen ante la evidencia. Por ejemplo, si un grupo de población pequeño, pero con ingresos muy importantes, no está representado en la muestra de la encuesta, “… el valor total del ingreso expandido de la misma, aún sin la presencia del subreporte, debe ser inferior al correspondiente con la Contabilidad Nacional, que por su metodología y cobertura incluye en principio los ingresos de todos los perceptores, sin excepción…”. La ausencia de tal grupo de hogares en la muestra da lugar a una censura por truncamiento que puede llegar a ser sustancial. En consecuencia, el tercer supuesto no corresponde con la realidad. Si en el ajuste al SCNM se ignora al mencionado truncamiento, el resultado será la redistribución de una cantidad desconocida, y tal vez importante, entre los hogares incluidos en la muestra. En los hechos, se incrementarán los ingresos observados por la encuesta en diversas proporciones, lo que dará lugar a consecuencias impredecibles en la aplicación de la política social del Estado mexicano; por ejemplo, al reducir en gabinete el número de hogares en condiciones de pobreza. Concluye Leyva que la distinción entre subreporte y truncamiento no es trivial y que a la sazón no existía ningún procedimiento sólido que permitiera hacerla.

Altimir (1987) propone un método “… basado en la asignación de las discrepancias con las cuentas nacionales según el tamaño del ingreso para cada tipo de ingreso (sueldos y salarios, empresariales, renta de la propiedad, transferencias, ingresos en especie, etc.) en vez de tomar solo en cuenta el ingreso total…”. Entre sus cinco supuestos principales, que se refieren exclusivamente al subreporte, destacamos el segundo: “La magnitud total del subreporte de los ingresos por tipo es aproximada mediante la discrepancia entre los ingresos muestrales y la estimación correspondiente para ese tipo de ingreso proveniente de las cuentas nacionales, ya corregidos por diferencias conceptuales, si aquel es menor que este…”. Y continúa diciendo que el “… procedimiento de ajuste consistió, por tanto, en ajustar separadamente los ingresos en la distribución de los hogares de cada grupo socioeconómico, mediante el coeficiente ponderado correspondiente al grupo asumiendo una elasticidad ingreso unitaria de subregistro, excepto los ingresos monetarios de la propiedad…”, suponiendo que “… el subregistro de los ingresos monetarios de la propiedad se concentra en el quintil más alto de hogares…”.

Para el caso en el que solo se dispone de la “… distribución general de los hogares por tamaño de ingreso, pero existe información sobre la composición del ingreso en cada segmento i, solo sería posible ajustar los ingresos en cada intervalo de acuerdo con la composición por tipo de ingreso, ya que los factores de ajuste en cada intervalo serían promedios ponderados de manera diferente de los factores de ajuste para cada tipo de ingreso…”, como se muestra en (1), donde  representa el monto de la discrepancia para el tipo de ingreso j. Entonces, el ingreso total ajustado  se calcula como la suma ponderada de los totales muestrales para cada tipo de ingreso , dentro de cada segmento de ingreso i:

                             

Esta expresión más simple permite observar con mayor claridad que los ingresos del mismo tipo son ajustados de manera proporcional a lo largo de todos los intervalos de ingreso, tal como ocurre en el caso general para el cual se da un tratamiento especial a los ingresos provenientes de la renta del capital/propiedad y en el que se consideran diversos grupos socioeconómicos. Hace evidente, asimismo, que Altimir decide ignorar el hecho de que la muestra solo es representativa de una subpoblación cuyos ingresos no llegan a ser desmesuradamente grandes.

A pesar de lo anterior, este es un procedimiento citado con frecuencia. La afirmación que Altimir hace en el sentido de que “… aunque inevitablemente arbitrario en sus supuestos, y limitado en sus aplicaciones por la desagregación de los datos disponibles, este método fue diseñado con el propósito de ajustar datos de ingreso de diferentes tipos de encuestas de una manera uniforme…”; parece indicar que detrás del método está la intención de llevar a cabo comparaciones entre los países de la región. Aunque su propuesta consigue el único propósito claramente establecido de reducir las discrepancias entre los resultados muestrales y los provenientes de las cuentas nacionales, no queda claro que el resultado sea óptimo en algún sentido. En efecto, hay un método, pero no un criterio. Tal vez por ello tiene que reducirse a una alternativa arbitraria en sus supuestos y limitada en sus aplicaciones.^[5]

Por lo que toca a las metodologías analizadas, Leyva establece que “… gravitan críticamente en los supuestos de cada autor acerca de las reglas de asignación que permiten distribuir entre los hogares o grupos de hogares, el valor de las diferencias entre los ingresos totales de los hogares reportados por las encuestas de ingresos y la Contabilidad Nacional…”. Afirma, además, que “… sin excepción, todas las reglas de asignación disponibles hasta el momento resultan arbitrarias…”.

Aunque en otro contexto, la polémica suscitada por el libro El capital en el siglo XXI, del economista francés Thomas Piketty (2014), ilustra que el problema comentado líneas arriba para México ha estado, y continúa, presente también en otras latitudes. Una de las críticas^[6] más difundidas a los resultados presentados en la publicación provino de Chris Giles, editor económico de The Financial Times (FT). En ella, ataca la credibilidad de Piketty argumentando que cometió una serie de errores de naturaleza diversa que sesgan sus hallazgos. De hecho, Giles afirma que, después de corregir los aparentes errores, no encuentra evidencia de que la concentración de la riqueza haya aumentado en los 30 años más recientes. En su respuesta,^[7] Piketty demuestra que algunas de las correcciones practicadas por el FT son menores y no alteran sus conclusiones; otras se basan en elecciones metodológicas que son debatibles. Encuentra Piketty que, entre las opciones metodológicas del FT, es particularmente problemático su uso de fuentes fiscales para las décadas iniciales y el cambio a estimadores muestrales para periodos más recientes. Y continúa, “… es problemático ya que sabemos que en todo país las encuestas sobre riqueza tienden a subestimar la participación de los más ricos en contraste con estimadores basados en datos administrativos fiscales…”. Por ello, dichas opciones metodológicas pueden sesgar los resultados hacia la declinación de la desigualdad.

Paul Krugman participa en el mismo debate.^[8] Sugiere que los supuestos errores señalados por Giles son, en esencia, “… los tipos de ajustes de datos que son normales en cualquier investigación que se apoya en una variedad de fuentes…”. Continúa diciendo, “… a riesgo de aportar demasiada información, este es el punto. Tenemos dos fuentes de evidencia tanto sobre ingreso como sobre riqueza: encuestas por muestreo, en las que se pregunta a las personas acerca de sus finanzas, y datos fiscales. Los datos muestrales, aunque útiles para dar seguimiento a las clases pobres y medias, subestiman notoriamente la riqueza y los ingresos más altos —en términos llanos— porque es difícil entrevistar suficientes billonarios. De este modo, los estudios sobre el 1%, el 0.1%, y otros semejantes se apoyan principalmente en datos fiscales…”.

Leyva-Parra (2004) concluye: “… cabe señalar que incluso si efectivamente las cifras de ingresos de los hogares de la Contabilidad Nacional pudieran considerarse como más verosímiles que las de la ENIGH, persistiría el problema de que aún no se ha desarrollado un criterio de asignación óptimo que permita establecer el puente para distribuir las diferencias macroeconómicas a nivel microeconómico. Este problema se complica cuando se considera el hecho de que las Cuentas Nacionales y la ENIGH hacen referencia a universos de hogares distintos, en virtud de que hay una fracción que se sospecha importante de los ingresos que se reportan en las estadísticas macroeconómicas (que se supone incluyen a todos los grupos de hogares), las cuales no se captan en las encuestas tipo ENIGH, lo que implica la existencia de un truncamiento (al menos) en la parte alta de la distribución del ingreso. Así, incluso en el caso de que se dispusiera de una regla de asignación óptima para pasar de lo macro a lo micro, sería necesario saber qué parte de la discrepancia de la ENIGH con las Cuentas Nacionales corresponde al subreporte y cuál, al truncamiento…”.

Ante la dificultad de asignar la proporción del déficit representada por cada una de las anteriores causas, ha sido usual actuar como si ninguna o solamente una de las dos estuviera presente. Por supuesto, ello puede llevarnos a tomar decisiones contra cuyos sesgos habrá que estar prevenidos. Con fines de ejemplificación, consideren el uso de los valores del ingreso sin modificación alguna, según fueron declarados en la encuesta. Bajo estas condiciones, al no tomar en cuenta la subdeclaración, se exagerará la proporción de hogares que exhibirá un ingreso inferior a una cantidad dada.^[9] Es decir, esta proporción resultará ser mayor que la que se alcanzaría si los ingresos hubieran sido ajustados por subdeclaración. No es difícil pensar que, en estas condiciones, medidas tales como la prevalencia de pobreza por ingresos lleguen a ser sobreestimadas. De manera similar, la ausencia de ingresos extraordinariamente grandes entre los datos muestrales podría también llevarnos a una subestimación de la desigualdad de ingresos.

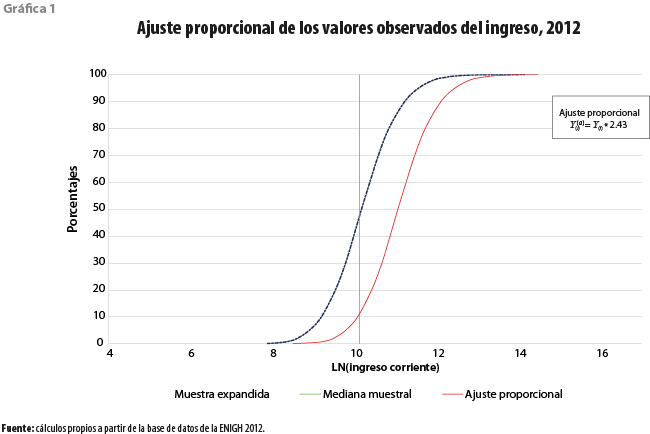
La distribución del ingreso es una de las estadísticas más referidas tanto en revistas especializadas como en diarios y noticieros. Sus aplicaciones son múltiples en estudios de pobreza, de desigualdad y aún de recaudación fiscal. Por otro lado, si se supone que la discrepancia es debida exclusivamente a la subdeclaración del ingreso en la encuesta, puede sugerirse que, de acuerdo con algún criterio, los valores declarados sean incrementados de modo que la suma expandida de los nuevos valores coincida con el total de cuentas nacionales. Aunque lo anterior puede resolver el problema de la discrepancia, añade incertidumbre para fines de política pública, pues la proporción del ingreso que sería explicado por truncamiento va a ser distribuido entre los hogares en la muestra, lo que puede dar lugar a un incremento excesivo de sus respectivos ingresos. Considérese entonces el caso de aquellos hogares cuyos ingresos declarados se encuentran cercanos, pero por debajo de una línea de pobreza por ingresos. Es posible pensar que, en algunos de estos casos, el nuevo ingreso resulte mayor a la mencionada línea de pobreza. Los hogares en estas condiciones no serán incluidos en la estimación del porcentaje de los que se encuentran en condiciones de pobreza. Es claro que proceder de este modo puede dar lugar a una subestimación de magnitud desconocida de las cifras de pobreza. Lo que ocurra con la medición de la desigualdad de ingresos dependerá de la forma o el método utilizado para realizar el ajuste, pero probablemente decrecerá. La gráfica 1 ilustra el efecto de realizar un ajuste deficiente a los datos del ingreso según las encuestas en hogares. Supongamos por un momento que la mediana de la distribución del ingreso obtenida a partir de los datos muestrales aporta una estimación razonable a lo que consideraríamos una línea de pobreza por ingresos. De manera gruesa, esto implicaría que la mitad de los hogares del país, cuyos ingresos se encuentran por debajo de dicha línea, son considerados en pobreza.

Más aún, supongamos que, ya que para nuestros fines basta con que la suma expandida de los datos ajustados , coincida con el total estimado por el Sistema de Cuentas Nacionales, consideramos adecuado el ajuste que multiplica a las cifras observadas Y_(i) por 2.43, como sería el caso de México para el 2012. Obsérvese que la proporción de hogares considerados en pobreza se reduciría a alrededor de 12 % si la línea de pobreza no presentara desplazamiento alguno después de llevar a cabo el ajuste. Debe ser claro que semejante éxito de la política social no es sino el resultado de un truco aritmético, que satisface la única condición impuesta sobre la suma expandida de los valores ajustados.

Por último, también se corren riesgos cuando se supone que el truncamiento explica totalmente la discrepancia entre ambas estimaciones. En este caso, autores como Campos et al. (2014), siguiendo a Lakner y Milanovich^[10] (2013), han seguido el curso de no aplicar modificación alguna a los ingresos de los hogares que se encuentran en los primeros ocho deciles de la encuesta de ingresos, de modo que la discrepancia entre las fuentes es distribuida en diferentes proporciones entre los que ocupan los dos deciles mayores. Por lo que toca a los ingresos menores, aquellos asociados con condiciones de pobreza, regresamos a la situación discutida párrafos arriba en la que los ingresos no son sometidos a ajuste alguno. En otras palabras, es probable que la magnitud de la pobreza sea sobreestimada sin que se pueda determinar la dimensión de dicha sobreestimación causada por ignorar la presencia de subdeclaración para esos niveles de ingreso. Por supuesto, mediciones de la desigualdad por ingresos crecerán más allá de lo que parecería un límite razonable.

En el trabajo de Campos et al., la distribución del ingreso que obtienen siguiendo el anterior procedimiento se vincula con la tributación óptima y con la captación posible. Es claro que la imagen posiblemente distorsionada^[11] de dicha distribución puede conducir a la conclusión de que la captación de ingresos fiscales obtenida hoy en día es muy inferior a la que tendría lugar si sus supuestos se cumplieran. Si el encargado de elaborar la política de ingresos del gobierno federal tomara estos resultados de forma acrítica, no es difícil pensar que llegaría a la conclusión de que la magnitud de la evasión fiscal alcanzaría niveles importantes. Las mismas decisiones que tomaría con base en resultados tan inciertos podrían conducirle a, por ejemplo, instrumentar ajustes fiscales que podrían conducir a mayores déficits gubernamentales, pues los ingresos efectivamente tributados no alcanzarán el nivel esperado, según estas estimaciones.

En la siguiente sección se hará un breve recuento de la metodología desarrollada para obtener los resultados que se presentan más adelante. A lo largo de esta investigación se ha recurrido a nuestra propuesta original que se ha denominado criterio de máxima pseudo-verosimilitud restringida (MPVR). También, se hace referencia a algunos resultados publicados con anterioridad con el fin de facilitar la comprensión del material. El lector interesado podrá recurrir a los trabajos de Bustos (2015 a, b) y Bustos y Leyva (2017). La segunda sección exhibe el comportamiento de los resultados de aplicar dicha metodología a datos mexicanos entre los años 2010 y 2016, tanto a nivel nacional como desagregándolos por entidad federativa. Finalmente, la última incluye consideraciones acerca de la metodología, sobre sus extensiones, así como algunas sugerencias para trabajo futuro de investigación.

 

Metodología

Ante todo, es necesario dejar claro que nuestra investigación pretende encontrar una aproximación a la distribución del ingreso de los hogares en México aprovechando de la mejor manera posible la información disponible. No pretende, como ha sido el caso con otros trabajos relacionados (por ejemplo, Martínez,1970 y Félix,1979), producir una base de datos con valores ajustados del ingreso. Más aún, dado que “… el supuesto referido a la regla de asignación es en realidad sólo un buen deseo ya que, sin excepción, todas las reglas de asignación disponibles hasta el momento resultan arbitrarias…” (Leyva, 2004), nosotros hemos decidido iniciar estableciendo con toda claridad el criterio de optimalidad que debe guiar nuestra búsqueda de soluciones en la estimación de la distribución del ingreso. En este sentido, el contraste es claro, las propuestas revisadas por Leyva (2004) han resultado en datos ajustados que satisfacen que su suma expandida coincida con el valor aportado por el SCNM. Sin embargo, no es posible concluir cuáles entre ellas son mejores en algún sentido razonable, pues han sido obtenidas recurriendo a supuestos ad hoc, y sin hacer explícita la medida de eficiencia usada. Se puede suponer que esta es otra de las razones por las cuales la medición oficial de la pobreza en México al inicio del siglo XXI no hace uso de ninguna de tales propuestas de ajuste.^[12]

En resumen, la metodología usada en el presente trabajo para obtener los resultados que se discutirán es la propuesta en Bustos (2015.a), que tiene el siguiente objetivo: hacer un uso óptimo,^[13] según el criterio MPVR, de la información disponible para estimar una distribución del ingreso corriente de los hogares en México que sea más cercana a la realidad y que resulte menos arbitraria, sin hacer imputaciones ni correcciones a los datos de la ENIGH.

El criterio utilizado busca maximizar la pseudo-verosimilitud para la muestra, tomando en cuenta la información proveniente de otras fuentes, incorporada a manera de restricciones que deben ser satisfechas por los valores del vector de parámetros. Dicho planteamiento apareció por primera vez en Bustos (2015.a), y queda expresado como se muestra en (2):

                        

donde:

representa al logaritmo natural de la función de densidad, evaluada en el i-ésimo valor muestral del ingreso Y_(i), como función del vector de parámetros θ cuyo valor óptimo se pretende determinar.

π_(i), a la probabilidad de inclusión correspondiente a dicha unidad muestral.

h(θ), a la(s) función(es) de los parámetros cuyos valores están restringidos a tomar valores específicos dados en el vector c (ej., SCN) y cuya forma está vinculada a la particular distribución de que se trate.

λ, a un vector de multiplicadores de Lagrange de dimensiones apropiadas.

Con base en los ingresos trimestrales de los hogares de la ENIGH 2012, se ajustaron dos distribuciones de probabilidad:

• Gamma generalizada (GG).
• Beta generalizada tipo II (GB2).

Las formas funcionales de  y de h varían con cada selección de distribución. En todos los casos se impuso una restricción: h(θ) = E[Y|θ] = Ingreso trimestral promedio por hogar, según el SCNM. Para considerar la información aportada por los registros fiscales anonimizados, se incluyó una segunda. El cuadro 1 resume la forma que han tomado las restricciones usadas a lo largo del desarrollo del proyecto. La primera de ellas obliga a los parámetros del modelo, incluidos los del ajuste óptimo, a tomar valores tales que el promedio de la distribución ajustada coincida con el que se determina a partir de la información del Sistema de Cuentas Nacionales de México.^[14] La segunda obliga a coincidir a los promedios de los ingresos de los hogares que ganan más que el umbral φ_α, tanto según el modelo como el Sistema de Administración Tributaria (SAT).^[15]

A manera de ejemplificación sobre las ventajas de incorporar información adicional, referimos al lector a los coeficientes de Gini obtenidos en Bustos (2015.a) y en Bustos et al. (2017). En el primer caso, al no contar con acceso a registros fiscales, solo se hizo uso de la primera restricción resultando en valores del Gini cercanos a 0.8, para el modelo óptimo. Por su parte, una vez incorporada la información del SAT, los valores reportados para el coeficiente de Gini se ubicaron entre 0.61 y 0.64, para los cuatro ajustes reportados. En ambos casos, los ajustes se realizaron usando información de la ENIGH 2012, la cual reportó un valor del coeficiente de Gini igual a 0.44, subestimando la desigualdad según los resultados anteriores. Análisis posteriores permitieron establecer que, por ejemplo, el umbral correspondiente a un millonésimo de los hogares para el ajuste con una sola restricción resultaba tener un valor 10 veces más grande que lo reportado por la base de datos de declaraciones fiscales para ese año. En otras palabras, dicho primer ajuste tomaba ingresos correspondientes a los deciles inferiores para transferirlos a los superiores resultando en una aparente sobreestimación del ingreso recibido por hogares en los deciles de ingresos más altos; consecuentemente, de acuerdo con estos resultados, la desigualdad de ingresos también sería sobreestimada. Es claro, por otro lado, que las políticas de recaudación fiscal que es posible instrumentar en uno u otro caso mostrarían también diferencias y montos importantes.

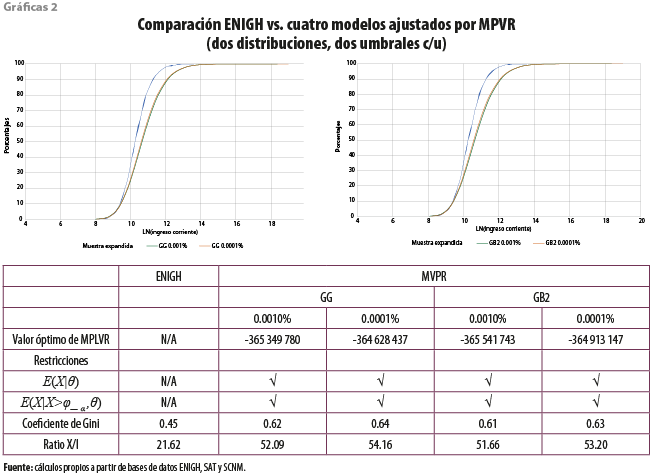
A partir del segundo conjunto de resultados, queda claro que las restricciones impuestas tienen un peso importante en su determinación. En efecto, se realizaron cuatro ajustes considerando dos umbrales diferentes para cada una de las distribuciones. El cuadro que acompaña a las gráficas 2 muestra un resumen de resultados relevantes. Se observará que los valores óptimos del criterio utilizado exhiben una variabilidad muy pequeña. Se apreciará, asimismo, que algo semejante ocurre tanto para los coeficientes de Gini como para las relaciones entre el ingreso total del primero y el décimo deciles, denotado por Ratio X/I. A nuestro juicio, los umbrales utilizados hacen poca diferencia; los modelos empleados hacen todavía menos diferencia. A causa de lo anterior, debe quedar claro que en este contexto pierde relevancia el argumento frecuentemente utilizado en el sentido de que el uso de modelos, aunque en contextos diferentes, es arbitrario.

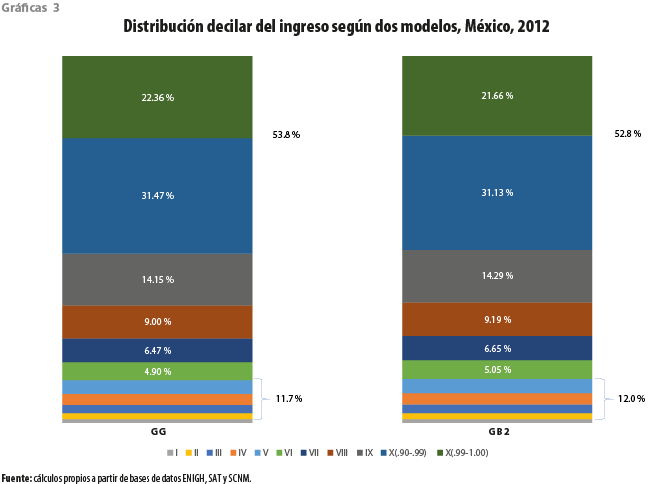
Como puede observarse en las gráficas 3, la consideración de agregados gruesos, como por ejemplo las participaciones en el ingreso de cada uno de los deciles de la población de hogares, parecen reflejar una importante semejanza entre los modelos alternativos. Es claro que las acumuladas en el ingreso de los primeros cinco deciles exhiben una diferencia de apenas 0.3 por ciento. Por su parte, la participación del último decil se encuentra entre 52.8 y 53.8 % del total. Las de 1 % con mayores ingresos difieren en menos de 1 por ciento.

Los anteriores resultados numéricos, en particular la indiferencia entre los modelos, nos llevan a pensar que se ve reducida la arbitrariedad en su elección, así como el peso de los supuestos que la misma conlleva, al considerar el uso simultáneo de fuentes, contra lo que ocurre en otras aplicaciones y contextos.

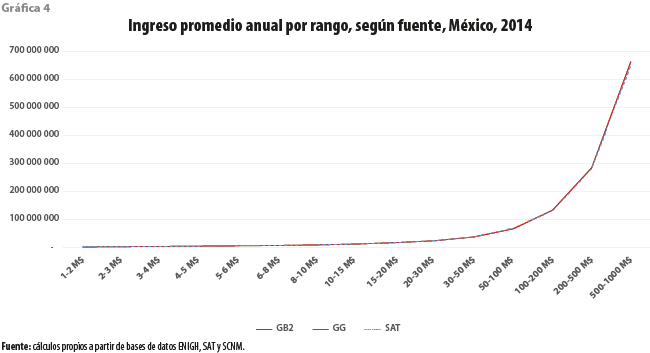
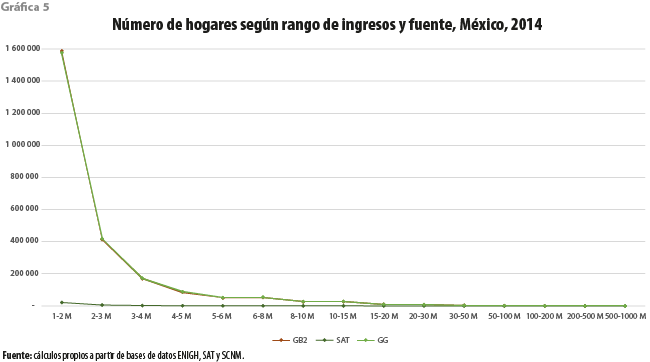
La gráfica 4 presenta una importante coincidencia entre los promedios de ingresos según la base de datos del SAT y los que se calculan a partir de los modelos ajustados, cuando los hogares son clasificados en rangos según su ingreso. La gráfica 5, en cambio, que muestra el número de hogares en cada rango de ingreso, exhibe diferencias importantes entre ambos conjuntos de cálculos, en particular en los rangos bajos de ingresos. Al menos, en parte, la mencionada diferencia parece ser consecuencia del supuesto introducido al hacer uso de la información fiscal; es decir, de utilizar una base de datos cuya unidad de observación es el individuo y no el hogar. En tanto dicho supuesto no parece tener grandes consecuencias para los ingresos altos, el número de individuos cuyo ingreso se encuentra en uno de los rangos inferiores resultará menor que el de hogares cuyo ingreso, que es la suma de lo percibido por cada uno de sus integrantes, cae en el mismo rango. Es claro que estos hogares no son perceptibles a partir de la base de datos de las declaraciones de las personas físicas. Así es, a medida que nos alejemos de los ingresos altos, el efecto de las diferentes unidades de observación se tornará más importante. Desde luego, no se descarta que otras causas, tales como nuestro otro supuesto sobre la confiabilidad del dato del Sistema de Cuentas Nacionales de México o la subdeclaración fiscal, estén presentes en las diferencias mostradas. Desafortunadamente, carecemos de información que nos permita determinar la importancia relativa de cada una de ellas.

El ingreso en México a lo largo del tiempo y de la geografía

En la presente sección, a través de un conjunto de resúmenes estadísticos, trataremos de ilustrar la forma en la que nuestros resultados exhiben, primeramente, la evolución de la distribución del ingreso a lo largo del tiempo; acto seguido, se añade la consideración de su distribución geográfica. Para estos fines, se hará uso de las bases de datos de la ENIGH, o de su Módulo de Condiciones Socioeconómicas (MCS^[16]), del INEGI; de las anonimizadas de declaraciones fiscales del SAT; así como de los resultados publicados para el sector institucional de hogares del SCNM. Todos ellos para los años 2010, 2012, 2014 y 2016. Asimismo, en todos los casos, el modelo ajustado a los anteriores datos será la gama generalizada con restricciones (GGc).

Evolución de la desigualdad en México, 2010-2016

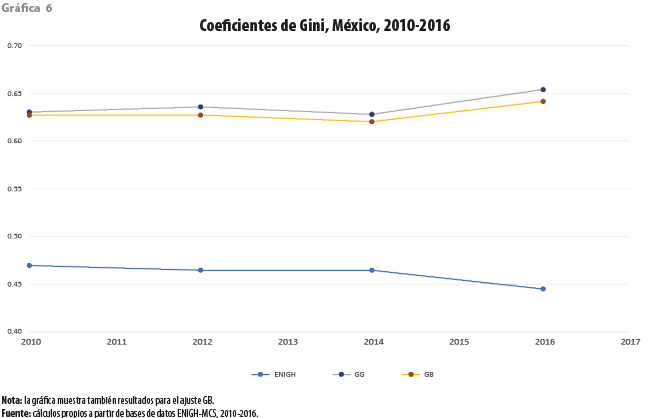
En una primera instancia, concentraremos nuestra atención en el estudio de la desigualdad a lo largo de diversas dimensiones. La gráfica 6 muestra la evolución del coeficiente de Gini a partir tanto de las respectivas ENIGH como del ajuste de la distribución gama generalizada, imponiendo la restricción asociada al umbral un millonésimo, a lo largo del periodo de estudio. Como podrá observarse, la brecha entre ambas líneas tiene una magnitud casi constante excepto, tal vez, para el último año. En efecto, en tanto, para la encuesta no hay una modificación importante del valor del coeficiente de Gini; para el modelo ajustado, la desigualdad exhibe un incremento que le lleva por vez primera durante el periodo por encima de 0.65.

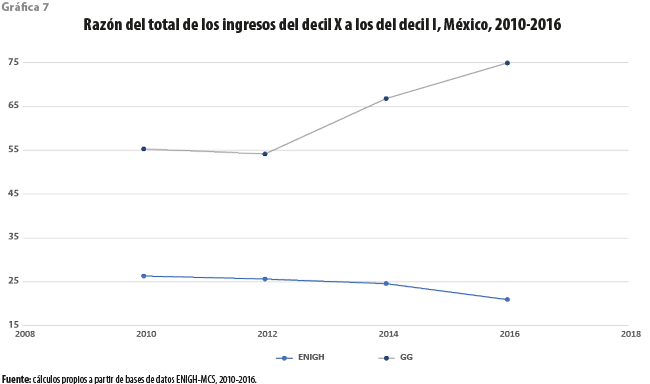
La razón del total de los ingresos del decil X a los del primero contrasta los ingresos de los dos conjuntos de hogares, cada uno compuesto por 10 % del total, en ambos extremos de la distribución; es decir que, a diferencia del coeficiente de Gini, ignora los resultados para los deciles intermedios. La gráfica 7 parece indicar que, para la encuesta, las brechas entre los extremos han venido reduciéndose al quedar este valor por debajo de las 25 veces. Por su parte, los ajustes por MPVR, que inician con un decremento del primero al segundo año de los considerados, muestran que esta discrepancia ha venido creciendo hasta alcanzar el valor del mayor las 75 veces el valor del menor.

En otras palabras, los valores de las dos estadísticas consideradas, los cuales no se ven afectados por la inflación, exhiben las aparentes ventajas de hacer un uso más eficiente de la información disponible. En efecto, las imágenes que pintan ambos conjuntos de resultados en nuestras mentes, así como las conclusiones que con fines de política pública es posible extraer de ellas, son contrastantes. Para el caso de los coeficientes de Gini, podría pensarse que los cambios introducidos en la metodología de la encuesta a partir del 2015 podrían haber dado como consecuencia un comportamiento anómalo para el 2016. Sin embargo, cuando consideramos el segundo conjunto de resultados, se puede concluir que la brecha entre ambos ejercicios ya había empezado a incrementarse desde el 2014; es decir, por lo menos un año antes de la introducción de modificaciones a la encuesta. Con base en lo anterior, resulta difícil ignorar la inequidad que se observa en ambos casos para el 2016.

La desigualdad entre entidades federativas, 2010-2016

Es también importante desagregar los resultados anteriores por lo menos hasta el nivel de entidad federativa. Con este fin, se recurrió a los MCS de la ENIGH para los mismos años atendiendo a su mayor tamaño de muestra estatal. A partir de esta información se ajustó un modelo para cada uno de los estados siguiendo el procedimiento anteriormente descrito. Para ello, en vista de la ausencia de información para el sector institucional de los hogares a nivel de entidad, se tornó necesario aproximar la participación estatal porcentual en el ingreso nacional para dicho sector. Aunque se dispone de la que resulta de la propia encuesta, en vista de la subestimación de los totales del ingreso, se decidió intentar el uso de otras fuentes.

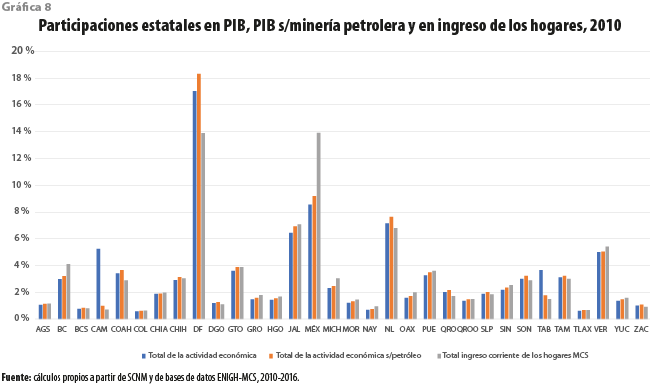
La primera opción fue hacerlo a través de la participación del Producto Interno Bruto Estatal (PIB-E) en el nacional para cada uno de los años, con base en el supuesto de que este y el ingreso total de los hogares por entidad estarían altamente correlacionados. Sin embargo, el PIB de algunas entidades muestra una fuerte influencia de la actividad de extracción de petróleo. Ya que el ingreso por dicha actividad se distribuye a lo largo de todo el territorio, la participación de su PIB-E sobreestima la del ingreso de los hogares en esos estados. Lo anterior nos condujo de manera natural a nuestra segunda opción, dada por el valor del propio PIB-E, pero del cual se ha restado el valor de la minería petrolera. Como muestra la gráfica 8, la distribución porcentual obtenida de esta forma reduce la participación de las entidades petroleras que exhiben mayor concordancia con la que se obtiene para el ingreso a partir de la encuesta.

Sin embargo, son aún perceptibles dos discrepancias importantes, ahora para entidades no petroleras, según puede apreciarse de la gráfica 8, que ejemplifica para el 2010 la participación porcentual de los estados, tanto en el PIB nacional como en el que no contempla la minería petrolera, y en el ingreso nacional de los hogares. Se trata tanto de la Distrito Federal (hoy Ciudad de México o CDMX) como del estado de México, las que presentan una importante interacción mutua. En efecto, una muy importante parte de la Zona Metropolitana de la Ciudad de México se encuentra localizada en el estado de México. Los residentes en los municipios conurbados trabajan, estudian, compran y se divierten en gran medida en la CDMX, contribuyendo a aumentar el valor de su PIB. Sin embargo, su ingreso es declarado a la encuesta en el lugar donde tienen su residencia.

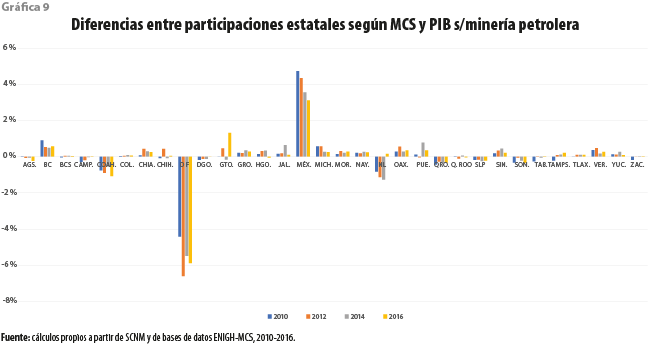
Por lo anterior, recurrir a la participación aportada por el PIB sin la minería petrolera sobreestima la contribución de la CDMX en el ingreso nacional de los hogares, mientras que la del estado de México sería subestimada. Con un PIB agregado que alcanza casi 25 % del PIB nacional, el error de aproximación cometido no podría ser ignorado. La gráfica 9 ilustra como la Ciudad de México y el estado de México distorsionan la participación del ingreso por su alta interdependencia.

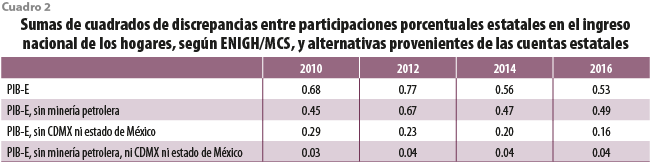
El cuadro 2 muestra las sumas de cuadrados de las discrepancias entre la participación porcentual de las entidades en el ingreso nacional de los hogares según la encuesta y diversas cantidades obtenidas a partir de las cuentas estatales. La evidencia que ella aporta, así como la discusión precedente, nos permite concluir que de entre las tres opciones exploradas, la que aproxima de mejor manera la participación del ingreso estatal de los hogares es la que no introduce sesgos obvios. De esta manera, y en vista de que no se cuenta con otras fuentes igualmente confiables para aproximar la deseada participación, regresamos a nuestra primera intuición distribuyendo de forma proporcional el total nacional de ingresos, según la participación relativa aportada por la propia ENIGH/MCS.

De esta manera se obtuvo la versión estatal de una de las dos restricciones que hemos venido utilizando. En contraste, la base de datos del SAT aporta la entidad en la que se localiza el domicilio fiscal del declarante, por lo que pudo ser usada sin cambio para la segunda de las restricciones mencionadas. Con base en las anteriores consideraciones, es posible obtener un conjunto de resultados a nivel de entidad federativa. En vista de los menores tamaños poblacionales involucrados, los resultados pueden ser fuertemente influenciados por la ocurrencia fortuita de eventos extraordinarios como, por ejemplo, ganar un premio en algún sorteo importante.

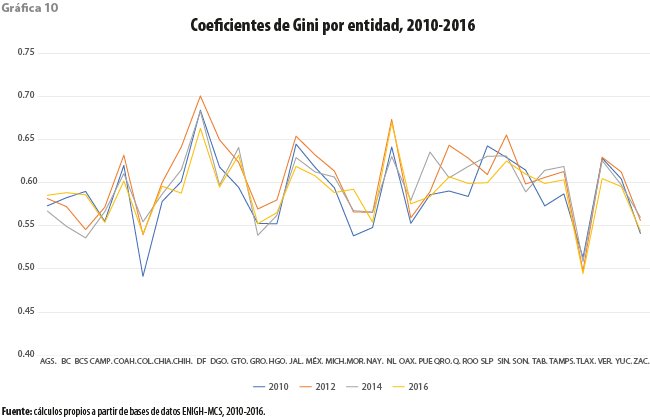
A partir de la gráfica 10 queda claro que, de acuerdo con los modelos ajustados, la desigualdad no se distribuye de manera uniforme a lo largo del territorio nacional. A pesar de la variabilidad que exhiben los valores ahí presentados, puede pensarse en la presencia de tres conjuntos de entidades. Al primero de ellos pertenecen aquellas cuyos valores se encuentran por arriba de 0.6 para todos los años considerados. Enseguida, tendríamos al conjunto para las cuales uno o más de los valores están por debajo de 0.6, en tanto que uno o más de ellos se encuentra por encima. Finalmente, se tienen aquellos estados cuyos coeficientes de Gini permanecen por debajo del mencionado valor.

Por otro lado, en tanto algunas de las entidades muestran comportamientos muy semejantes a lo largo del tiempo, otras más presentan una circunstancia cambiante. Vale la pena destacar que, en ninguno de los casos, el 2016 muestra las condiciones más extremas de desigualdad, contra lo que ocurre a nivel nacional. Lo anterior nos lleva a preguntar si es posible que al interior de los estados sea posible que tenga lugar una reducción de la desigualdad cuando, entre ellas, se da un incremento.

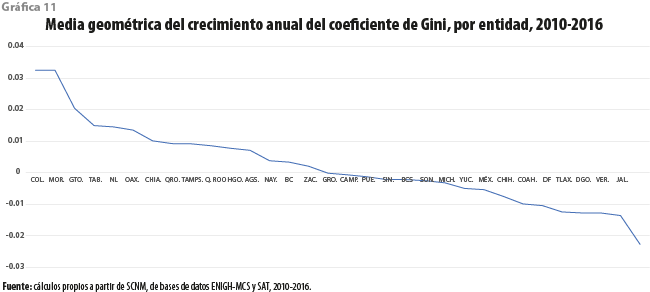
La gráfica 11 exhibe la tasa media de crecimiento del coeficiente de Gini, por entidad, para el periodo 2010-2016. Casi la mitad de las entidades muestran un crecimiento para los valores de dicho coeficiente, por lo que en ellas la desigualdad parece haber crecido. Es necesario precisar que un ritmo alto de crecimiento en la desigualdad puede deberse a un valor pequeño al inicio del periodo, como puede ser el caso para Colima y Morelos. Por otro lado, se debe destacar que dos de las entidades con más alta desigualdad en el 2010, Nuevo León y Distrito Federal (hoy Ciudad de México), muestran en cambio trayectorias divergentes; el valor del coeficiente creció para la primera, en tanto que para la segunda ocurrió lo opuesto. Son estos movimientos en sentidos opuestos para los estados los que nos llevan a pensar que la creciente desigualdad nacional pueda ser explicada más en términos del comportamiento de la desigualdad entre ellas que del que se presenta a su interior.

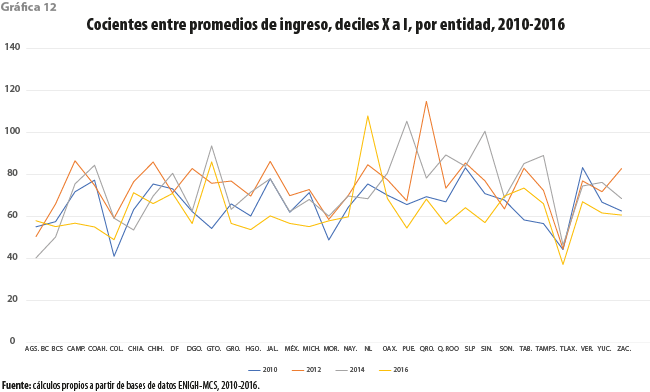
La anterior pregunta es también aplicable cuando se consideran las comparaciones entre los totales de ingresos para los dos deciles extremos. A partir de la gráfica 12 observamos que, ni para el 2014 ni para el 2016, tales cocientes son uniformemente mayores para todas las entidades. De hecho, es posible apreciar que, para este último año y para una alta proporción de los estados, los valores de los cocientes resultan ser mínimos al compararse con los de todo el periodo. Lo anterior nos ha hecho sospechar que podríamos estar frente a una situación como la descrita en Lakner (2013), donde se afirma que “… la mayor parte de la desigualdad global es explicada por diferencias entre los países, aunque esta contribución ha declinado a lo largo del tiempo, sugiriendo que los países se han hecho más parecidos. La componente intra-país de la desigualdad global, sin embargo, ha crecido continuamente…”.

Evidencia de trayectorias divergentes de la marginación municipal en México, entre 1990 y el 2010, ha sido documentada en Vargas y Cortés (2016), quienes afirman que sus resultados “… proporcionan evidencia clara de que la marginación en México ha sido decreciente, pero con aumento en la heterogeneidad entre los municipios en los últimos 20 años. Dicho de otro modo, si bien la marginación ha disminuido en las dos últimas décadas, el país ha experimentado, a nivel municipal, un proceso de divergencia y no de convergencia territorial…”. Aplicado al caso de la desigualdad de ingresos, lo anterior permitiría responder positivamente las preguntas planteadas arriba afirmando que es posible que al interior de las entidades la desigualdad disminuya, cuando entre ellas crece.

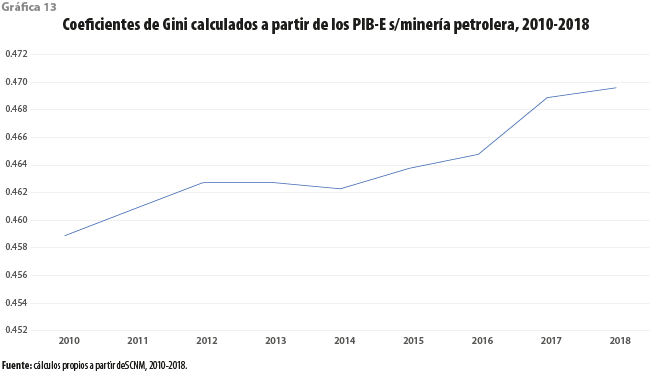
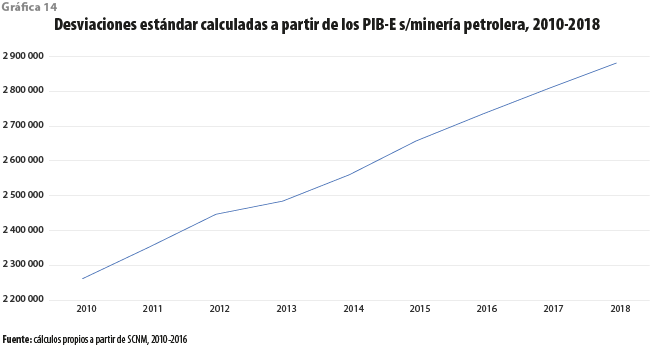
De hecho, con la información publicada por el INEGI para el periodo, es posible calcular medidas de desigualdad a partir de los PIB estatales, sin la minería petrolera. Las gráficas 13 y 14 muestran la evolución del coeficiente de Gini y de la desviación estándar, calculados a partir de dichos PIB. En ambos casos es aparente una tendencia creciente entre el 2010 y 2018. En otras palabras, la desigualdad entre las entidades creció en el periodo, según el SCNM. Este incremento puede ayudar a resolver, así sea parcialmente, la aparente paradoja entre el aumento en la desigualdad de ingresos a nivel nacional, pero no al estatal.

Comentarios finales

Hemos hecho un breve recuento de la metodología MPVR y de algunos de sus resultados. En cuanto a esta, se destacan tres posibilidades con base en los resultados:

1.     Los datos de la encuesta tienen un papel que jugar en cada ajuste, pero las restricciones impuestas reducen su importancia de modo que sus limitaciones también pierden peso.

2.     Los modelos usados en el contexto de dicha metodología juegan también un papel menor.

3.     La comparación entre distribuciones ajustadas de ingreso y estadísticas derivadas se lleva a cabo entre las mejores opciones en cada caso, dada la información disponible.

Por lo que toca a los resultados numéricos, aunque a nivel nacional la desigualdad empeoró entre el 2010 y 2016, salvo por algunas excepciones, al interior de las entidades federativas no se aprecia un deterioro importante. Ello nos ha llevado a postular que la desigualdad entre los estados es un factor importante que debe ser tomado en cuenta al intentar explicar su comportamiento a nivel nacional, a lo largo del tiempo. En este momento no disponemos de evidencia suficiente para rechazar dicha conjetura. Sin embargo, se presenta evidencia derivada del SCNM que apoyaría esta afirmación.

Para los resultados anteriores, se cuenta en el caso mexicano con muchos elementos comunes que permiten realizar comparaciones: diseño de muestra, tratamiento para valores faltantes del ingreso, percentiles similares de ingreso según el SAT, asignación del promedio estatal de ingresos según el SCNM y la ENIGH, por mencionar algunos. Los organismos internacionales tienen una tarea más complicada al intentar llevar a cabo comparaciones entre naciones a partir de resultados muestrales. Procedimientos como el sobremuestreo de hogares con ingresos altos o la calibración de resultados con totales exógenos han sido realizados por algunos países, pero no por todos. En consecuencia, se torna más importante cuando se desea llevar a cabo comparaciones entre naciones a lo largo del tiempo, contar con procedimientos estándar que reduzcan el peso de las diferencias, pero evitando el uso de procedimientos ad hoc.

Por lo que se refiere a trabajo futuro relacionado con la misma metodología, en este momento estamos explorando:

1.     El uso de mezclas de distribuciones con lo que se aumenta el número de parámetros a estimar y, en consecuencia, el de fuentes alternativas y de restricciones que es posible considerar en el ajuste.

2.     Identificar con precisión a la población representada por la muestra mediante el uso de funciones truncadas.

3.     Aproximar la proporción que la subdeclaración del ingreso representa de la discrepancia total, así como la que corresponde al truncamiento.

4.     Imputar valores del ingreso para unidades muestrales en la base de datos de la encuesta para atender las necesidades de algunos usuarios.

___________

Fuentes

Altimir, O. “Income distribution statistics in Latin America and their reliability”, en: Review of Income and Wealth. 33(2), 1987.

Boghosian, B. M. “Is inequality inevitable?, originally published with the title ‘The Inescapable Casino’”, en: Scientific American. 321, 5, pp. 70-77, November 2019 (DE) https://bit.ly/3czU4go

Bustos, A. Estimation of the distribution of income from survey data, adjusting for compatibility with other sources. Workshop on Measuring Inequalities of Income and Wealth, High-Level Expert Group on the Measurement of Economic Performance and Social Progress. Berlin, Sep. 15-16, 2015.a (DE)  https://bit.ly/3Txifg2

_______ “Estimation of the distribution of income from survey data, adjusting for compatibility with other sources”, en: Statistical Journal of the IAOS. 31, pp. 565-577, 2015.b (DE) https://bit.ly/3CKeVZb

Bustos, A. y G. Leyva. “Towards a More Realistic Estimate of the Income Distribution in Mexico”, en: Latin American Policy. Volume 8, Issue 1, pp. 114-126, June 2017 (DE)  https://bit.ly/3RUQmgv Hernández

Campos Vázquez, R., E. Chávez Jiménez y G. Esquivel. Los ingresos altos, la tributación óptima y la recaudación posible. Primer lugar, Premio Nacional de Finanzas Públicas, 2014.

Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL). Metodología para la medición multidimensional de la pobreza en México. Tercera edición. Ciudad de México, CONEVAL, 2019 (DE) https://bit.ly/2Ffih9w

Cortés-Cáceres, F. “El cálculo de la pobreza y la desigualdad a partir de la Encuesta Nacional de Ingresos y Gastos de los Hogares”, en: Comercio Exterior. Vol. 51, Núm.10, octubre. México, 2001.

DESA. Principles and Recommendations for Population and Housing Censuses, Revision 3. New York, Statistics Division, Department of Economic and Social Affairs, United Nations, 2017 (DE) Series_M67rev3-E.pdf (un.org) consultado el 18 de junio de 2020.

Economic Commission for Latin America and the Caribbean (ECLAC). “Income poverty measurement: updated methodology and results”, en: ECLAC Methodologies. No. 2 (LC/PUB.2018/22-P), Santiago, 2019 (DE) https://bit.ly/3pXYKzT consultado el 28 de septiembre de 2022.

Félix, David. “Income distribution Trends in Mexico and the Kuznets Curves”, en: Weinart, Richard y Cynthia Hewlett. The Political Economy of Brasil and Mexico. Philadelphia, ISMI Press, 1979.

Fesseau, M. and P. van de Ven. “Measuring inequality in income and consumption in a national accounts framework”, en: OECD Statistics Brief. No. 19, pp. 1-10, Nov. 2014.

Instituto Nacional de Estadística y Geografía (INEGI). Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH). México, INEGI, 2014 (DE) https://bit.ly/2VEt0yb consultado el 5 de septiembre de 2022.

_______ Nueva construcción de la ENIGH 2012. Tabulados. México, INEGI, 2014 (DE) https://bit.ly/3L5PhAe consultado el  5 de septiembre de 2022.

_______ Sistema de Cuentas Nacionales de México. Fuentes y metodologías. Año base 2013. Cuentas por Sectores Institucionales. México, INEGI, 2017 (DE) https://bit.ly/2BFmG2G

Lakner, Ch. y B. Milanovic. “Global Income Distribution: From the Fall of the Berlin Wall to the Great Recession”, en: World Bank policy research paper. 6719, 2013.

Leyva-Parra, G. El ajuste del ingreso de la ENIGH con la Contabilidad Nacional y la medición de la pobreza en México. Serie Documentos de investigación. Núm. 19. México, SEDESOL, 2004.

Martínez de Navarrete, Ifigenia. La distribución del ingreso en México: tendencias y proyecciones a 1980. Vol. 1. México, D.F., Siglo Veintiuno Editores, 1970.

Piketty, T., El capital en el Siglo XXI, Fondo de Cultura Económica, México, D. F., 2014.

UNECE, Canberra Group. Handbook on Household Income Statistics. Second Edition. Geneva, United Nations, United Nations Economic Commission for Europe, 2011.

Vargas, D. y Cortés, F. “Análisis de las trayectorias de la marginación municipal en México de 1990 a 2010”, en: Cordera et al. (coords.). Por un México social: contra la desigualdad. México, Universidad Nacional Autónoma de México, 2016.

^[1] El lector interesado podrá extender esta información en UNECE (2011).

^[2] A manera de ejemplo, la información en este apartado puede ser ampliada, para el caso mexicano, en la sección Documentación de la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH), en la siguiente URL: https://bit.ly/2rlM8nP

^[3] INEGI. Sistema de Cuentas Nacionales de México. Fuentes y metodologías. Año base 2013. Cuentas por Sectores Institucionales, https://bit.ly/2BFmG2G

^[4] OCDE, “For Good Measure: Advancing Research on Well-Being Metrics Beyond GDP”, en Chap. 6: Distributional national accounts.

^[5] La propuesta de Altimir parece haber sido usada por la Comisión Económica para América Latina y el Caribe (CEPAL) para el cálculo de incidencia de la pobreza en los países de esa región. Recientemente, la CEPAL (2019) ha eliminado este procedimiento y trabaja con los datos de las encuestas sin ajustarlos. Al recurrir a la identificación de una población de referencia mediante el método que denominan de quintiles móviles, los cuales parecen surgir de la propia encuesta, argumenta que “… el ajuste de ingresos no mejora la plausibilidad, comparabilidad o confiabilidad de las mediciones de pobreza…”. Por supuesto, ello ocurre ya que el método de ajuste no modifica las posiciones relativas de los hogares.

^[6] https://bit.ly/3RkVKt2

^[7] https://bit.ly/3KASwiX

^[8] https://nyti.ms/3KD3bd4

^[9] Como los 2 dólares diarios, según la paridad de poder de compra, usados por el Banco Mundial.

^[10] Estos autores ajustan por el consumo, no el ingreso, a diferencia de Campos y coautores.

^[11] “… tal ajuste puede parecer excesivo […] cuando la media muestral es igual a solo 50% del consumo privado (NT: como llega a ocurrir en México con el ingreso) entonces simplemente asignar este 50% al decil más alto es probablemente excesivo…”, Lakner et al. (2013, p. 38).

^[12] En CONEVAL (2019), pp. 100-101, se establece que uno de los criterios usados es “… Emplear la información de ingresos captada bienalmente por el INEGI en la ENIGH…”, sin hacer referencia a algún ajuste.

^[13] El término óptimo hace referencia a un criterio explícito (por ejemplo, MPVR). Intenta comparar con propuestas para las cuales no es posible determinar si un cambio cualquiera da lugar o no a un mejor resultado numérico, por carecer de dicho criterio explícito. Es posible pensar que, con base en otros criterios, nuestros resultados dejarían de ser óptimos.

^[14] En México, en el 2012, dicho promedio era de 86 410.57 pesos; por lo anterior, todas las funciones ajustadas tienen una media de casi 86 410. El equivalente reportado por la ENIGH para el 2012 se encuentra en casi 38 mil pesos.

^[15] Se usó el supuesto de que los ingresos de personas físicas mayores a un umbral muy alto son equivalentes a los de un hogar, ya que la base de datos anonimizada de declaraciones anuales de las personas físicas en el SAT no permite agregar los ingresos por hogar.

^[16] Por ejemplo, https://bit.ly/3wLJh9T