Análisis econométrico para determinar la relación entre la confianza del consumidor y la actividad económica de la frontera norte de México
Econometric Analysis to Determine the Relationship between Consumer Confidence and Economic Activity in the Northern Border of Mexico
Genny Patricia Esparza Ruiz,* Francisco de Jesús Corona Villavicencio* y Edgar Jiménez Peña**
* Instituto Nacional de Estadística y Geografía (INEGI), genny.ruiz@inegi.org.mx y franciscoj.corona@inegi.org.mx, respectivamente.
** Centro de Investigación en Matemáticas, A. C. (CIMAT), ejimenez@cimat.mx.
Vol. 14, Núm. 3 – Epub Análisis econométrico…– Epub
|
En este trabajo se realiza un análisis econométrico para determinar la relación existente entre el Indicador de Confianza del Consumidor (ICC) con respecto a la actividad económica de la frontera norte del país, lo anterior con el objetivo de desentrañar la capacidad explicativa y predictiva del ICC con respecto a las economías de las entidades de esa zona geográfica. Para lo anterior, primero se determina qué tipo de transformación del Indicador Trimestral de la Actividad Económica Estatal (ITAEE) maximiza la correlación con respecto al ICC, se analizan las propiedades estocásticas de las series y se estima un vector autorregresivo, concluyendo que el ICC está relacionado de manera significativa con los ITAEE respectivos y, asimismo, es causal en el sentido de Granger. En este contexto, los resultados permiten concluir que el ICC puede ser usado como un elemento predictor de la variación anual del ITAEE para esas entidades. Palabras clave: causalidad en el sentido de Granger; Indicador de Confianza del Consumidor; Indicador Trimestral de la Actividad Económica Estatal; transformaciones; vectores autorregresivos. |
In this paper an econometric analysis is carried out to determine the relationship between the Consumer Confidence Indicator (CCI) with respect to the economic activity of the northern border of the country, with the objective of unraveling the explanatory and predictive capacity of the CCI with respect to the economies of the above-mentioned entities. First, we determine what type of transformation of the Quarterly Indicator of State Economic Activity (ITAEE) maximizes the correlation with respect to the CCI, analyze the stochastic properties of the series and estimate an autoregressive vector, concluding that the CCI is significantly related to the respective ITAEE and, likewise, is causal in the Granger sense. In this context, the results allow us to conclude that the CCI can be used as a predictor of the annual variation of the ITAEE for these entities
Key words: granger causality; Consumer Confidence Indicator; Quarterly Indicator of State Economic Activity; transformations; autoregressive vector.
|
Recibido: 21 de febrero de 2023.
Aceptado: 23 de mayo de 2023.
- Introducción
El uso de indicadores económicos en México tiene diferentes fines, por ejemplo, explicar alguna relación estructural entre variables o bien predecir el comportamiento de un fenómeno macroeconómico. En consecuencia, es sabido que nuestra economía está muy sincronizada con la de Estados Unidos de América (EE. UU.), motivo por el cual se suele explicar las variaciones del Producto Interno Bruto (PIB) del país en función de la variabilidad del PIB de EE. UU. (ver, por ejemplo, Herrera, 2004). También, el Indicador Oportuno de la Actividad Económica (IOAE) se basa en construir un factor dinámico altamente correlacionado con el Indicador Global de la Actividad Económica (IGAE), ambos del Instituto Nacional de Estadística y Geografía (INEGI), de tal forma que, usando una vasta cantidad de información de aspectos económicos, financieros y fuentes no tradicionales, se predice de manera oportuna el comportamiento del IGAE (ver Corona et al., 2022). Estos ejemplos son aplicaciones comunes en el campo de la econometría de las series de tiempo, pero existen otras muchas relaciones empíricas que son provechosas de analizar.
En este contexto, una pregunta de interés en la coyuntura económica de México es desentrañar qué tipo información otorgan los indicadores de difusión, principalmente el Indicador de Confianza del Consumidor (ICC), que genera el INEGI, el cual surge de la Encuesta Nacional sobre Confianza del Consumidor (ENCO),[1] que fue creada con el objetivo general de producir información estadística, cualitativa y cuantitativa, para obtener indicadores sobre la percepción actual y las expectativas a futuro que tiene la población acerca de su situación económica, la de su familia y la del país (INEGI, 2016); de las posibilidades de compra de bienes de consumo duradero y efímero; además de otras variables de tipo económico que son importantes, como el empleo, la inflación y el ahorro; por ello, el ICC puede ser usado, al menos desde una perspectiva empírica, para predecir en el corto plazo el comportamiento de la economía.
Sin embargo, a la fecha, no son muchos los trabajos que se orienten en estudiar si el ICC tiene capacidad explicativa o predictiva con respecto a indicadores económicos tradicionales, como pudiesen ser el IGAE o el Consumo Privado. En López-Pérez et al. (2022) se realiza un estudio que tiene como objetivo utilizar las componentes del ICC para generar un indicador alternativo que esté altamente correlacionado con estos dos últimos mediante el uso de mínimos cuadrados parciales encontrando, también, la ventana temporal en la cual se maximiza la correlación entre el ICC con las variables de interés. Otra investigación relevante es la de Leyva et al. (2016), donde se estudia cómo se conforma el ICC, concluyendo que es más apropiado utilizar las componentes de este como indicadores de balance en lugar de índices para tener una mejor capacidad interpretativa.
Para otras economías, Deés y Soares-Brinca (2011) analizan cómo la confianza del consumidor puede ser usada para predecir el gasto de consumo tanto para la economía de EE. UU. como para la zona Euro. También Lahiri et al. (2016) estudian su capacidad predictiva para pronosticar, en tiempo real, el gasto en consumo en nuestro vecino del norte dentro del contexto de modelos de factores dinámicos, concluyendo que el uso de este indicador disminuye el error de estimación. Nótese que estos resultados discrepan, en cierto sentido, con lo obtenido por Loría y Brito (2004), quienes determinan que, para la economía de Estados Unidos de América, el ICC no está cointegrado con la inversión privada y el consumo y que, además, no es causal en el sentido de Granger, sin embargo, sí se ve afectado en el corto plazo por las variaciones de estos. Otro trabajo interesante es Malovaná et al. (2021), quienes encuentran que variables relacionadas con el entorno macroeconómico de los hogares están altamente relacionadas con los ICC publicados de manera oficial por la Organización para la Cooperación y el Desarrollo Económicos (OCDE).
Aunque estas investigaciones son importantes para entender algunas de las utilidades del ICC en el contexto macroeconómico de México y otras economías, ninguno de ellos profundiza de forma puntual sobre cuál es su capacidad explicativa y predictiva relativo a economías específicas. En consecuencia, en el presente trabajo se plantea una metodología econométrica con la finalidad de dar respuesta a este cuestionamiento. Específicamente, el objetivo de nuestro estudio es determinar la utilidad del ICC para explicar y predecir el comportamiento de la economía de la frontera norte del país. Nos enfocamos en las entidades federativas de esa zona geográfica, ya que representan 26 % del total del PIB nacional (INEGI, 2022), a la par de que son economías con particularidades de interés, como ser altamente industriales y dependientes de Estados Unidos de América. Nótese que el ICC es un indicador de sentimientos, pues recaba estados de ánimos sobre la situación actual y futura. Esto hace atractivo también su uso para explicar y predecir las variaciones de la economía fronteriza de México.
Con el fin de cumplir con este objetivo, proponemos realizar lo siguiente: i) determinar qué tipo de transformación (ninguna, variación trimestral o anual) del Indicador Trimestral de la Actividad Económica Estatal de cada entidad maximiza la correlación con el ICC, ii) analizar las propiedades estocásticas de las series, iii) estimar un vector autorregresivo (VAR), iv) analizar las propiedades de los residuales y v) usar el modelo VAR con fines estructurales y predictivos.
Con lo anterior se desprende un objetivo transversal de interés, es decir, evaluar en qué entidades de la frontera norte del país el ICC tiene menor/mayor capacidad explicativa y predictiva, validada por la estimación de modelos consistentes desde una perspectiva estadística.
El resto del trabajo está organizado de la siguiente manera: en la sección II se presenta la metodología y el plan de acción, en la III se muestran la memoria de cálculo y los resultados y, finalmente, en la IV se concluye y se describen las recomendaciones.
2. Metodología
En esta sección se presenta la notación, la metodología y el resumen técnico que se emplean para cumplir con los objetivos planteados.
2.1. Transformación óptima
Definamos al ICCt e ITAEEt = (BCt, Sont, Chiht, Coaht, NLt, Tamt) para t = 1, … , T; por lo tanto, la transformación óptima del ITAEE que maximiza la correlación con el ICC se especifica de la siguiente manera:
ITAEE* = {ITAEE ǀ max Cor (ƒ(ITAEE), ICC)} (1)
donde ITAEE = (ITAEE1,…, ITAEET) e ICC = (ICC1, …,ICCt)′ En palabras, la expresión (1) indica que se busca una matriz del ITAEE, la cual se obtiene como aquella que maximiza la correlación entre una forma funcional de este con respecto al vector que contiene los elementos del ICC. En específico, las formas funcionales a probar son: ninguna, variación trimestral y variación anual.
2.2. Pruebas de raíces unitarias: aumentada de Dickey-Fuller (ADF)
Para cada una de las variables del modelo, Yt = (ITAEEt ,…, ICCt ), se estima la regresión ADF (ver, por ejemplo, Banerjee et al., 1993) con el fin de estimar el estadístico que permite concluir sobre la posible presencia de raíces unitarias. Esta se especifica como sigue:
donde yt representa una variable en particular de Yt, co es la constante de la regresión, t es una tendencia determinística, c1, β y γi son coeficientes asociados de cada uno de los regresores, p es un operador del rezago máximo a considerar y et es un error que se asume ruido blanco. Si la serie no tiene raíz unitaria, podemos concluir que es estacionaria y esto ocurre cuando rechazamos la hipótesis nula definida como H0: β = 0. Cabe mencionar que los rezagos óptimos se pueden seleccionar usando el criterio de Akaike (AIC) o Schwarz (SC) considerando hasta siete rezagos posibles y se estima la prueba Ljung-Box a los residuales de la regresión ADF para asegurarnos de que los errores no tienen correlación serial.
2.3. Vectores autorregresivos
El modelo VAR(p) se especifica como sigue:
Yt = A1 Yt-1 + … ApYt-p + εt, (3)
donde εt es un término de error con comportamiento de ruido blanco y las matrices de coeficientes, Aj, son de dimensión 7 × 7 .
Asumiendo que el modelo básico (3) es estacionario en covarianza, supuesto que tomamos como dado, dicha expresión se puede escribir como modelos de regresión lineal de la siguiente forma:
yi= ZAi + ei, i=1,…,K, (4)
donde yi es un vector de T × 1 de i observaciones en la ecuación i. La matriz Z tiene la forma de (3) en Yt–1 siendo de dimensión T × Kp, Ai es un vector de Kp × 1 parámetros y ei es un vector de T × 1, que contiene los términos de error con matrices de covarianzas δi IT. De esta forma, cada ecuación puede ser estimada por mínimos cuadrados ordinarios (MCO) de manera separada sin perder eficiencia respecto a mínimos cuadrados generalizados. Nótese que en este caso K = 7.
El rezago óptimo, p, se determina usando los siguientes criterios de información:
donde ![]() es el factor de penalización por el número de observaciones y parámetros. En la práctica se suelen utilizar los criterios AIC, SC y Hannan-Quinn (HQ), cuyas penalizaciones son, respectivamente,
es el factor de penalización por el número de observaciones y parámetros. En la práctica se suelen utilizar los criterios AIC, SC y Hannan-Quinn (HQ), cuyas penalizaciones son, respectivamente, ![]() .
.
Para verificar que los errores no están autocorrelacionados, se utiliza la prueba Portmanteau-Breusch-Godfrey, que se especifica como sigue:
donde 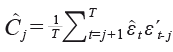 . El estadístico se encuentra distribuido aproximadamente como una
. El estadístico se encuentra distribuido aproximadamente como una ![]() , donde h es el rezago máximo por probar y la hipótesis nula denota la no presencia de errores autocorrelacionados. Por último, para evaluar la posible presencia de efecto ARCH, se utiliza la siguiente expresión:
, donde h es el rezago máximo por probar y la hipótesis nula denota la no presencia de errores autocorrelacionados. Por último, para evaluar la posible presencia de efecto ARCH, se utiliza la siguiente expresión:
donde ![]() es la matriz de covarianza de los errores del modelo VAR para
es la matriz de covarianza de los errores del modelo VAR para ![]() . El estadístico se distribuye como x2(qK2 (k + 1)2/4), donde la hipótesis nula indica la no existencia del efecto ARCH. Para más detalles metodológicos sobre estas técnicas, ver, por ejemplo, Lütkepohl (2006).
. El estadístico se distribuye como x2(qK2 (k + 1)2/4), donde la hipótesis nula indica la no existencia del efecto ARCH. Para más detalles metodológicos sobre estas técnicas, ver, por ejemplo, Lütkepohl (2006).
2.4. Pruebas de causalidad de Granger
Para ejemplificar el uso de estas (Granger, 1969), supongamos un modelo VAR(p) bivariado donde si bajo hipótesis nula queremos probar que ICCt no es causal en el sentido de Granger, tendríamos entonces que especificar el siguiente modelo VAR:
Lo anterior puede generalizar esta idea para modelos VAR(p) de dimensión k, lo cual es equivalente a probar si los coeficientes Aj son estadísticamente equivalentes a 0 para las variables posiblemente no causales.
2.5. Pronósticos
Para pronosticar valores futuros de Yt, podemos utilizar la cadena de pronóstico como sigue:
donde YT + h ǀ T = YT + h para h ≤ 0. Se puede mostrar que el h error de pronóstico viene dado por:
donde las matrices Ψs son determinadas por recursión de la siguiente manera:
Con Ψ0 = Ik y Aj = 0 para j > p. Entonces, la matriz de covarianza del error de pronóstico viene dada por:
Puede mostrarse que el mejor predictor Yt + h de es Yt + h ǀ T, el cual se obtiene al estimar ![]() a través de MCO de tal forma que la estimación de ∑(h) es como sigue:
a través de MCO de tal forma que la estimación de ∑(h) es como sigue:
donde ![]() Finalmente, el intervalo de confianza asintótico (1-a)100 % se especifica como:
Finalmente, el intervalo de confianza asintótico (1-a)100 % se especifica como:
donde C1– α / 2 es el (1 1¯ α / 2) cuantil de la distribución normal y σi (h) el i-ésimo elemento de la diagonal de ∑(h).
2.6. Resumen técnico: paso a paso
A continuación, se mencionan las fases de la rutina empírica empleada en el paquete estadístico R, los cuales tienen como finalidad satisfacer los objetivos planteados en esta investigación:
- Se trimestraliza el ICC promediando los valores mensuales que nos generan la frecuencia de cada tres meses (se usa la función ta de la librería tempdisagg).
- Se evalúa qué forma funcional del ITAEE maximiza la correlación con el ICC. Se prueban los niveles, variación trimestral y la variabilidad anual de las series. Las trimestrales y anuales son calculadas usando el logaritmo natural de las series aplicando el operador en diferencias con uno y cuatro rezagos, respectivamente. Seleccionamos aquella variación que, en promedio, genera el valor más alto.
- Se realizan pruebas de raíces unitarias ADF de manera individual a cada una de las series para verificar si estas son estacionarias o no. Se consideran todas las especificaciones en la prueba ADF: ninguna, constante, así como constante y tendencia (se usa la función adf).
- Se determina el rezago óptimo utilizando el criterio SC (se utiliza VARselect de la librería vars).
- Se estima el modelo VAR empleando una variable exógena atribuible al segundo trimestre del 2020 que aísla el efecto de la pandemia de la COVID-19 (se usa la función VAR de la librería vars).
- Se realiza el análisis de residuales al modelo VAR (se emplean serial.test y arch.test de la librería vars).
- Se lleva a cabo el análisis estructural del modelo: gráficos de ajuste y pruebas de causalidad de Granger (se usa la función causality de la librería vars).
- Se realizan predicciones con el modelo VAR y los ARIMA (se utiliza predict de la librería vars en el caso de VAR y las funciones auto.arima y forecast de la librería forecast para el caso de modelos ARIMA).
3. Resultados
En esta sección se presentan y describen los obtenidos.
3.1. Transformación óptima
Las series del ICC con la que realizamos el análisis comienzan a partir de abril del 2001 y finalizan en enero del 2022, mientras que para el ITAEE las tenemos a partir del primer trimestre de 1980 hasta el tercero del 2021. Ambas se trabajan de manera desestacionalizada, obtenidas así de la fuente oficial proveída por el INEGI. Una vez definida su longitud, estas se empatan en temporalidad de tal forma que tengamos un conjunto de datos homogéneo que permita hacer el análisis; es decir, en este caso, nuestro panel de información consta de siete variables observadas para 82 trimestres, de 2001/T2 a 2021/T3. Los datos fueron extraídos del Banco de Información Económica (BIE) del INEGI.
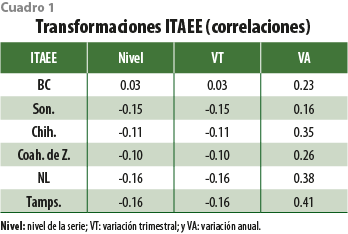
Hecho esto, como se mencionó en la sección anterior, el siguiente paso corresponde a encontrar la forma funcional en la que el ITAEE maximiza la correlación con el ICC, lo anterior mediante el uso de la expresión (1). El cuadro 1 resume los resultados.
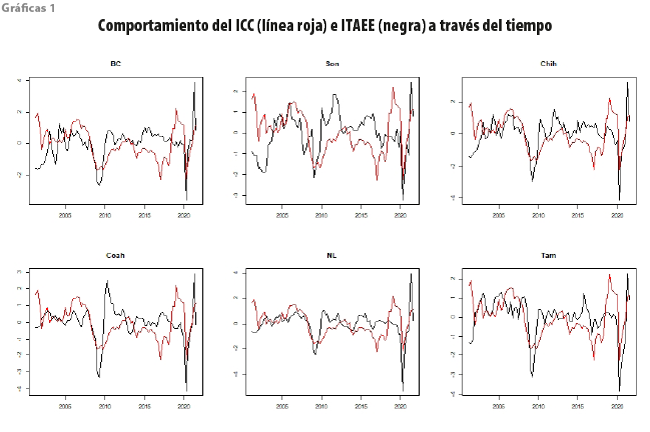
Se puede apreciar que los mejores resultados se obtienen al expresar al ITAEE en variaciones anuales; caso contrario, nótese que, incluso, se consiguen correlaciones negativas, lo cual es contraintuitivo debido a que esperaríamos que el ICC lo haga de manera positiva con las variaciones de la actividad económica. Una explicación del porqué las correlaciones son más altas cuando usamos la transformación anual es que el ICC es un indicador de difusión expresado en estos términos, pues muchas de las preguntas que lo conforman (ver Apéndice) corresponden a expectativas y/o comparaciones anuales, capturando, en cierto sentido, la evolución anual de la actividad económica. Las gráficas 1 resumen los comportamientos a través del tiempo al utilizar dicha transformación.
Los resultados gráficos corroboran lo obtenido en el cuadro 1. Nótese que, para el caso de Nuevo León y Tamaulipas, el ICC y los ITAEE están mayormente relacionados a través del tiempo, mientras que para Sonora se obtiene una relación más débil. Es interesante hacer ver que el ICC explica de manera coherente las crisis del 2009 y la más reciente atribuible a la pandemia de la COVID-19. También, es importante denotar que las series parecen moverse alrededor de un promedio, es decir, dan indicios de ser estacionarias, sin embargo, se requiere evaluar esto de manera formal, por lo que la siguiente sección muestra los resultados al utilizar la prueba ADF para los niveles de las series.
3.2. Prueba de raíces unitarias
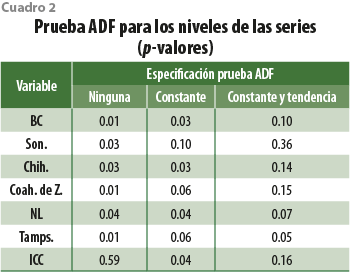
Con el objetivo de analizar las propiedades estocásticas de las series presentadas en las gráficas 1, el cuadro 2 resume los resultados de la prueba ADF para los niveles de las series usando las tres especificaciones posibles.
Se puede apreciar que, cuando la prueba ADF se precisa sin especificación alguna, en todos los casos se rechaza la hipótesis nula de no estacionariedad, con excepción del ICC. Cuando se utiliza una constante en la especificación, se rechaza en todos los casos con 10 % de significancia, mientras que, si usamos constante y tendencia, en muchos casos no rechazamos la hipótesis nula. Sin embargo, dado que en dos de las tres especificaciones tendemos a rechazar la hipótesis nula, a la par de que las gráficas 1 parecen indicarnos que las series de tiempo se mueven alrededor de un promedio, podemos concluir que las variables son estacionarias.
3.3. Vector autorregresivo
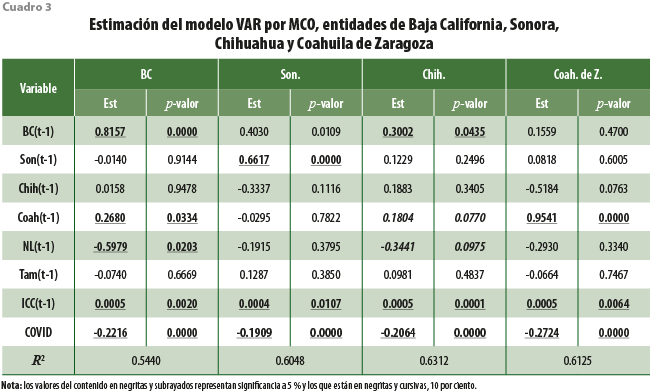
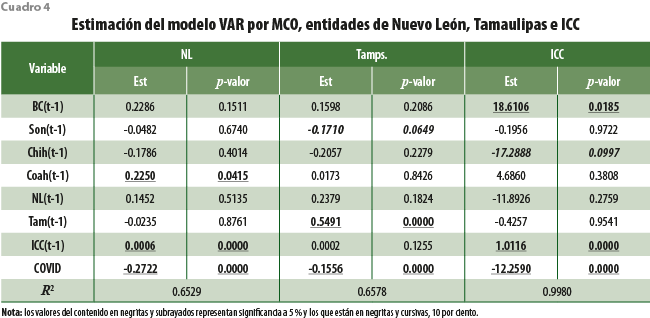
Una vez verificado el orden de integración de las series, se determina el rezago óptimo en el modelo VAR, concluyendo que, según el criterio SC, dicho rezago es cuando p = 1. En consecuencia, los cuadros 3 y 4 resumen los resultados de la estimación del VAR por MCO.
Se observan situaciones interesantes en la estimación del modelo VAR, donde varios coeficientes son relevantes. Por ejemplo, para Baja California, su rezago es significativo al igual que el de Coahuila de Zaragoza, Nuevo León y la variable del ICC, lo cual quiere decir que cuando las economías de estas entidades y el Indicador se incrementan en el trimestre anterior, la de Baja California se mueve en la dirección de los coeficientes. También, en todos los casos, la bondad de ajuste es superior a 54 % y la variable dummy de la COVID-19 siempre resulta significativa.
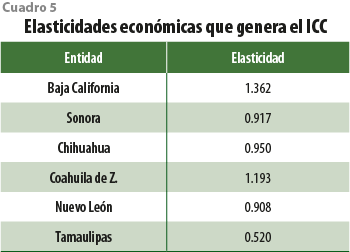
Es importante señalar que, en todos los casos, el ICC es significativo con excepción de la economía de Tamaulipas, y aunque los coeficientes que genera el Indicador son bajos, la interpretación debe realizarse con cautela, ya que, mientras los ITAEE están expresados en escala logarítmica y diferenciada, el ICC se encuentra en niveles de balance. En conclusión, se considera apropiado estimar las elasticidades para visualizar correctamente la magnitud (y signo) de los coeficientes estimados en los modelos VAR. Por dar tan solo un ejemplo, si se desea calcular la elasticidad que genera el ICC para Baja California, tenemos que![]() . En este sentido, el cuadro 5 muestra todas las elasticidades que produce el Indicador.
. En este sentido, el cuadro 5 muestra todas las elasticidades que produce el Indicador.
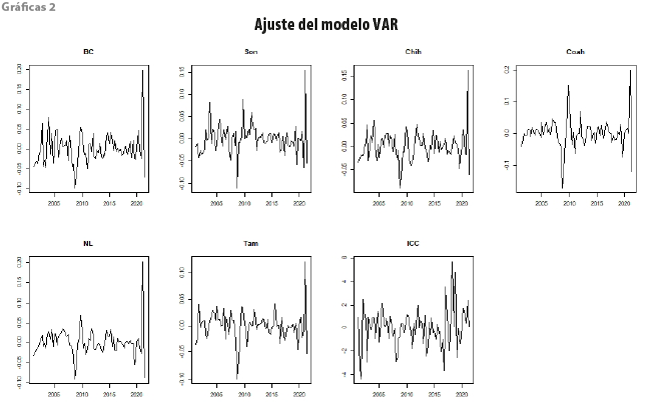
Se aprecia que en todos los casos es superior a 0.90 %, con excepción de la economía de Tamaulipas, donde a priori encontramos que el ICC no es significativo. En términos del ajuste que generan los modelos VAR para cada variable del vector Yt, las gráficas 2 muestra los resultados.
Se puede observar que el mejor ajuste es para la ecuación del ICC, y ello implica que el Indicador también se ve afectado por el comportamiento de las economías fronterizas, lo cual resulta coherente, ya que, conforme dichas economías de las entidades muestren mejor actuación, habrá una destacada percepción del presente y futuro y, por ende, el ICC tenderá a verse impactado. En general, que los ajustes sean relativamente altos, implica que: i) hay dependencias regionales entre las entidades de la frontera norte, ii) el ICC influye en la variación anual de la economía y iii) el ICC se ve también afectado por el comportamiento económico, es decir, la representación VAR modela de manera correcta las endogeneidades presentes.
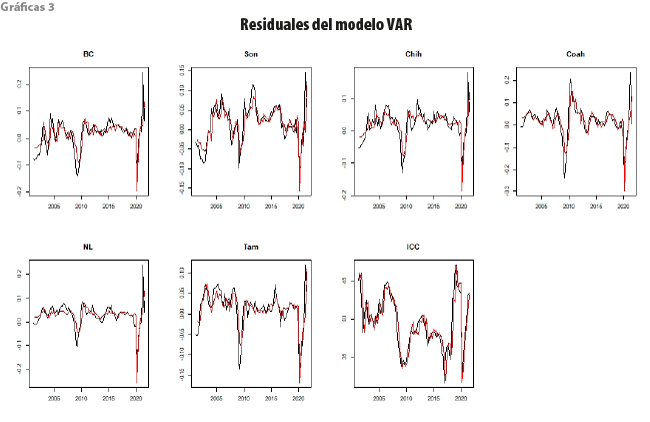
Resulta importante corroborar que los residuales estén correctamente comportados, motivo por el cual, en primera instancia, realizamos un análisis gráfico que se presenta en las gráficas 3.
Los residuales tienden a comportarse sin un patrón específico, con excepción de unas ligeras caídas presentadas en las crisis del 2009 y 2020, sin embargo, parecen no mostrar comportamiento autocorrelacionado ni una variabilidad que dependa del tiempo. Realizando las pruebas de las ecuaciones (6) y (7), es decir, las comprobaciones de autocorrelación y efecto ARCH, podemos concluir que los residuales no presentan dichos problemas al obtener p-valores de 0.1637 y 0.999, en ese orden. En este sentido, los coeficientes mostrados en los cuadros 3 y 4 están adecuadamente estimados y la interpretación del modelo es correcta y se prosigue a continuar con el análisis estructural de este y, también, predicciones individuales de las series.
3.4. Causalidad en el sentido de Granger
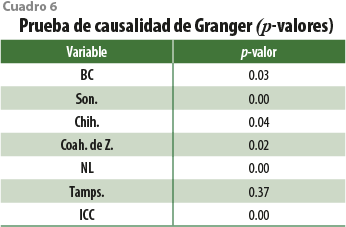
Con el objetivo de complementar el análisis estructural presentado en la subsección anterior, con el modelo mostrado en los cuadros 3 y 4 se realizan pruebas de causalidad de Granger para determinar si cada una de las variables tiene capacidad predictiva dentro del contexto del modelo. El cuadro 6 resume los resultados.
Es interesante observar que, con excepción de Tamaulipas, el resto de las variables, incluido el ICC, son causales en el sentido de Granger. Esto corrobora lo observado en la estimación del modelo VAR, ya que, si nos centramos en el renglón asociado a esa entidad, solo afecta a su economía y no al resto de las variables. Esta conclusión es potente desde un contexto econométrico, pues indica que corrobora que hay dependencias regionales en la frontera norte del país, excepto en Tamaulipas, la cual parece tener otra dinámica económica. También se concluye que el ICC es relevante para explicar y/o predecir el comportamiento de esa zona geográfica y este, a su vez, se ve afectado por el movimiento económico. Nótese que estos resultados son diferentes a los obtenidos por Loría y Brito (2004) para la economía de Estados Unidos de América, donde los autores encuentran que el Indicador no es causal para algunos componentes del PIB, como el consumo y la inversión privada.
3.5. Pronósticos
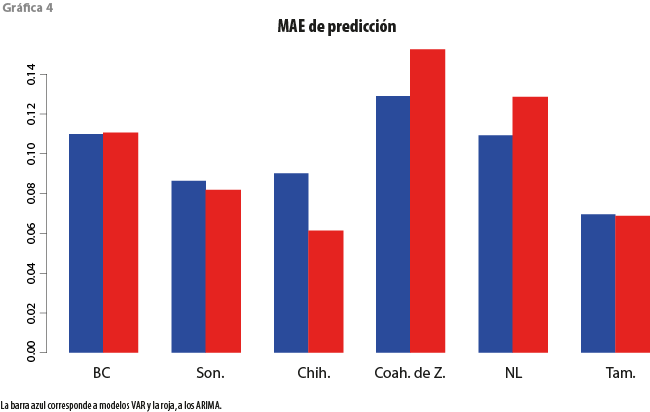
Con el objetivo de fortalecer el análisis de causalidad de Granger, se realizan predicciones en los siguientes sentidos (la gráfica 4 resume los resultados):
- Modelos VAR: predecir los anteriores siete trimestres (desde el 2020 al tercero del 2021), por pasos, con la especificación del modelo VAR obtenida en este trabajo. Nótese que este periodo abarca el de la COVID-19, lo cual es interesante para evaluar el funcionamiento con respecto a modelos univariados.
- Modelos ARIMA: predecir los anteriores siete trimestres, por pasos, con modelos univariados automáticos.
- Computar los errores absolutos de predicción (MAE, por sus siglas en inglés) para las entidades federativas y obtener el promedio.
Se puede observar que, en términos puntuales, ambos modelos generan errores de predicción muy similares aunque, si consideramos el promedio de todas las entidades analizadas, tenemos que el MAE del VAR es ligeramente menor con respecto al obtenido por los ARIMA (0.098 vs. 0.100) aun cuando, claramente, la prueba de Diebold y Mariano (1995) no permite rechazar la hipótesis nula de igualdad de pronóstico conjunto al obtener un p-valor de 0.3083. Sin embargo, dado los resultados del modelo VAR, donde concluimos que existen dependencias económicas regionales y la valía del ICC, lo cual se corrobora con la estimación de las pruebas de causalidad de Granger, se concluye también que, para fines de predicción, el VAR mostrado en este trabajo que tiene como artífice la presencia del Indicador resulta atractivo para predecir la actividad económica, en este caso, de la frontera norte del país. En este sentido, nuestros resultados son similares a los obtenidos por Deés y Soares-Brinca (2011) y Lahiri et al. (2016), quienes encuentran que el ICC tiene capacidad predictiva para pronosticar variables relevantes de la coyuntura económica de la zona Euro y los Estados Unidos de América.
4.Conclusiones y líneas futuras
Este trabajo se orientó en estudiar la relación empírica que existe entre el ICC y la actividad económica de la frontera norte de México medida a través de los ITAEE de las respectivas entidades federativas, lo anterior, mediante un marco metodológico econométrico. Específicamente, se determinó cuál es la transformación óptima del ITAEE que maximiza la correlación con el ICC, concluyendo que la mejor es la variación anual. Después, se corroboró la estacionariedad de las series a través de pruebas ADF y se especificó y estimó un VAR, concluyendo que: i) hay dependencias regionales entre las entidades de la frontera norte, ii) el ICC influye en la variación anual de las economías y iii) el Indicador se ve también afectado por el comportamiento económico. Asimismo, el modelo VAR no presentó problemas de autocorrelación serial y efecto ARCH, lo cual hace válidos los resultados desde una perspectiva estadística.
Las pruebas de causalidad de Granger permiten corroborar lo obtenido por el modelo VAR, concluyendo que hay dependencias regionales en la frontera norte del país, con excepción de Tamaulipas. Asimismo, el ICC tiene también capacidad explicativa y predictiva dentro del contexto del modelo.
Por último, se realizaron pronósticos para los siete trimestres anteriores incluyendo el tercero del 2021, concluyendo que el error de predicción disminuye ligeramente cuando se utiliza el ICC en comparación con modelos ARIMA.
Una posible interpretación estructural e importante de estos resultados puede ser que la percepción que tienen los agentes económicos se encuentra vinculada con la actividad económica, permitiendo describir, así como explicar y predecir, en este caso, el comportamiento de la economía de las entidades de la frontera norte del país. Lo anterior es trascendente también en términos de desarrollo económico, ya que esta parte del territorio mexicano se encuentra conectada con EE. UU., lo que conlleva a plantear una línea futura de trabajo, en este caso, incluir, el PIB de nuestro país vecino en el modelo VAR, entendiendo cómo es el comportamiento de la economía fronteriza a través de variables domésticas y de Estados Unidos de América.
Otra línea futura de interés es la de estimar un modelo de factores dinámicos, donde se usen conjuntamente las 32 economías y las 15 variables de la ENCO que componen al ICC, de tal forma que se analice la composición de los factores y sus propiedades estocásticas para, por último, evaluar la capacidad predictiva de estos con respecto a economías específicas. También, se considera hacer un análisis retrospectivo que abarque una mayor cantidad de trimestres, esto, para estimar de mejor forma la facultad de pronóstico de los modelos que se utilicen.
____________
Fuentes
Banerjee, A., J. J. Dolado, J. W. Galbraith y D. F. Hendry. Cointegration, Error Correction, and the Econometric Analysis of Non-Stationary Data. Oxford, Oxford University Press, 1993.
Corona, F., G. González-Farías y J. López-Pérez. “Timely estimates of the monthly Mexican economic activity”, en: Journal of Official Statistics (JOS). 38(3), 2022, pp. 733-765.
Deés, S. y P. Soares-Brinca. Consumer confidence as a predictor of consumption spending: Evidence for the United States and the Euro Area. Working Papers No. 1349, European Central Bank, 2011.
Diebold, F.X. and Mariano, R.S. (1995) Comparing predictive accuracy. Journal of Business and Economic Statistics, 13, 253-263.
Granger, C. W. J. “Investigating causal relations by econometric models and cross-spectral methods”, en: Econometrica. 37, 1969, pp. 424-438.
INEGI. Encuesta Nacional sobre Confianza del Consumidor 2015. Documento metodológico. Aguascalientes, México, INEGI, 2016.
_______ Banco de Información Económica (BIE). Aguascalientes, México, INEGI, 2022.
Herrera, J. “Business Cycles in Mexico and the United States: Do they Share common movements”, en: Journal of Applied Economics. 7(2), 2004, pp. 303-323.
Lahiri, K., G. Monokroussos e Y. Zhao. “Forecasting Consumption: The Role of Consumer Confidence in Real Time with many Predictors”, en: Journal of Applied Econometrics. 31(7), 2016, pp. 1254-1275
Leyva, G., O. Páez y S. M. Esperanza. “Un umbral empírico y otras recomendaciones para el reporte de la confianza del consumidor en México”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 7(1), 2016, pp. 112-121.
López-Pérez, J., F. Corona y J. M. Lecuanda. “Propuesta de indicadores alternativos para medir la confianza del consumidor”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 13(2), 2022, pp. 108-121.
Loría, E. y L. Brito. “Is the Consumer Confidence Index a Sound Predictor of the Private Demand in the United States?”, en: Estudios de Economía Aplicada. 22(3), 2004, pp. 795-809.
Lütkepohl, H. New Introduction to Multiple Time Series Analysis. New York, Springer, 2006.
Malovaná, S., M. Hodula y J. Frait. “What Does Really Drive Consumer Confidence?”, en: Social Indicators Research. 155, 2021, pp. 885-913 (DE) bit.ly/3YHKk7p.
__________________
Apéndice
Preguntas de la ENCO que componen al ICC
- Comparada con la situación económica que los miembros de este hogar tenían hace 12 meses, ¿cómo cree que es su situación en este momento?
- ¿Cómo considera usted que será la situación económica de los miembros de este hogar dentro de 12 meses, respecto a la actual?
- ¿Cómo considera usted la situación económica del país hoy en día comparada con la de hace 12 meses?
- ¿Cómo considera usted que será la condición económica del país dentro de 12 meses, respecto de la situación actual?
- Comparando la situación económica actual con la de hace un año, ¿cómo considera en el momento actual las posibilidades de que usted o alguno de los integrantes de este hogar realice compras tales como muebles, televisor, lavadora, otros aparatos electrodomésticos, etc.?
- ¿Cómo describe usted su situación económica comparada con la de hace 12 meses?
- ¿Y cómo cree usted que será su situación económica dentro de 12 meses, respecto de la actual?
- ¿En este momento tiene usted mayores posibilidades de comprar ropa, zapatos, alimentos, etc., que hace un año?
- ¿Considera usted que durante los próximos 12 meses usted o alguno de los integrantes de este hogar tendrán posibilidades económicas para salir de vacaciones?
- ¿Actualmente usted tiene posibilidades de ahorrar alguna parte de sus ingresos?
- ¿Cómo considera usted que serán sus condiciones económicas para ahorrar dentro de 12 meses comparadas con las actuales?
- Comparando con los 12 meses anteriores, ¿cómo cree usted que se comporten los precios en el país en los siguientes 12 meses?
- ¿Cree usted que el empleo en el país en los próximos 12 meses (aumentará, permanecerá igual, disminuirá…)?
- ¿Algún miembro de este hogar o usted están planeando comprar un automóvil nuevo o usado en los próximos dos años?
- ¿Algún miembro de este hogar o usted están planeando comprar, construir o remodelar una casa en los próximos dos años?
[1] Programa estadístico del INEGI.



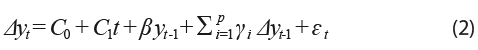
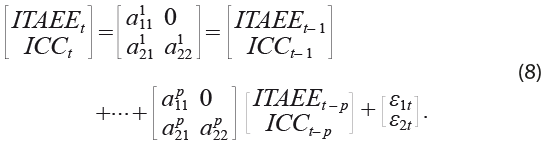
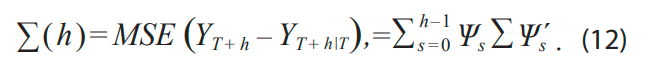
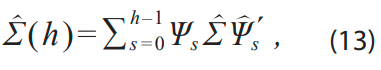
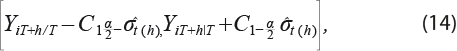


MUCHAS FELICIDADES!!!
Gracias por compartir este tipo de articulo documental ya que nos es de mucha utilidad a las personas que realizamos investigaciones y consultas al impacto económico de México y su política económica.
Es de mucha utilidad en materia de política económica independientemente que no somos 100% matemáticos, si manejamos estadísticas ante un derecho tributario comparativo; ya que en materia de impuestos impacta lo económico.
Espero leer más de sus artículos como este.
En hora buena.