Estimación markoviana del tamaño y de las estructuras de una población
|
El conocimiento del tamaño presente y futuro de la población de un país, así como de su estructura y distribución por edad, sexo y entidad federativa, es central para la planeación, presupuestación e instrumentación de diversas actividades públicas y privadas. Se reconoce que, en ausencia de registros oportunos y confiables, es imposible conocer dicho tamaño con precisión suficiente salvo tal vez para el momento a que se refiere un resultado censal. La mejor alternativa para cualquier otro periodo está en la estimación de la evolución de dicho tamaño a través de la consideración simultánea de las tasas de fecundidad, mortalidad y migración que afectarán a la población bajo estudio durante el periodo de estimación. Las matrices de transición, estructuras imprescindibles en el estudio de las denominadas Cadenas de Markov, se prestan de manera casi natural al estudio de la mencionada evolución, aunque requieren ajustes que permitan el cambio en el tamaño de la población de un periodo al siguiente. Su aplicación directa permite seguir la evolución del valor promedio del tamaño poblacional, como consecuencia de las tasas asumidas, para cada uno de los periodos futuros bajo consideración. Adicionalmente, dichas estructuras permiten determinar los tamaños probables de las variaciones alrededor de los promedios estimados a través de la simulación estocástica de la evolución de éstos un gran número de veces. En este trabajo, partiendo de las semejanzas entre algunas estructuras básicas de la demografía y las de las Cadenas de Markov, se presentan extensiones y precisiones a algunas propuestas en la literatura. Se mostrarán, también, algunas aplicaciones de los anteriores resultados al caso mexicano para la década 2000-2010 y se los compara con las estimaciones obtenidas por CONAPO. Se concluye que las estimaciones obtenidas a través de las extensiones presentadas corrigen deficiencias de los procedimientos utilizados hasta el momento con el mismo fin. Palabras clave: dinámica poblacional, mortalidad, fecundidad, migración, Cadena de Markov. |
Knowledge of current and future sizes of the population of a country, and its structure and distribution by age, sex and state, is central to the planning, budgeting and implementation of various public and private activities. It is recognized that in the absence of timely and reliable records, it is impossible to know such size with sufficient precision except perhaps for census years. The best choice for any other period is the estimation of the evolution of the size through the simultaneous consideration of fertility,1 mortality and migration rates that will affect the population under study during the estimation period. Transition matrices, indispensable structures in the study of Markov chains, lend themselves almost naturally to the study of these developments, although adjustments are required to allow for the change in population size from one period to the next. Their direct application allows us to follow the evolution of the population-size averages as a result of the assumed rates, for each and every one of the future periods under consideration. Additionally, such structures allow determining likely variations around estimated size averages through stochastic simulation of these developments a large number of times. In this paper, after making explicit the similarities between some basic structures of demography and Markov chains, we present some extensions and clarifications to proposals found in the literature. We will also show some applications of the above results to the Mexican case for the decade 2000-2010 and compare them with the estimates obtained by CONAPO. It is concluded that the estimates obtained through the presented extensions correct limitations of the procedures currently in use with the same end. Key words: Population Dynamics, Mortality, Fertility, Migration, Markov Chain. |
1. Introducción
1.1 Usos comunes para las cifras recientes del tamaño de una población
La información reciente relativa al tamaño de la población tanto de un país como de subpoblaciones relevantes, y que resulta de los censos de población, es contemplada en México y en otros países por diversos preceptos legales para apoyar en ella la toma de variadas decisiones. En general, destacan los usos que se hacen de ésta para acercarse a la proporcionalidad en la representación popular y los que se refieren a la asignación de recursos fiscales a las administraciones locales.
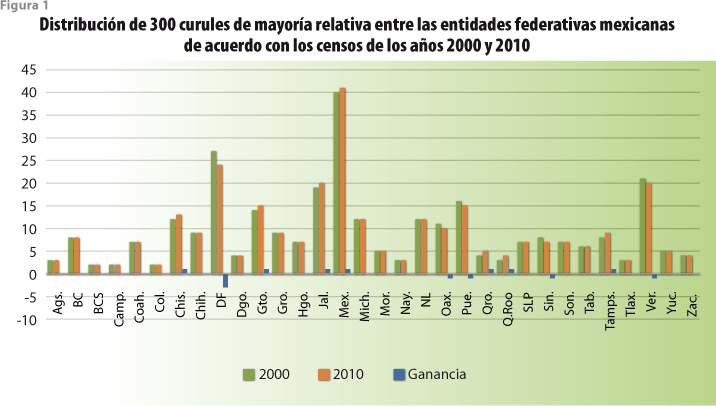
El propósito en el primero de estos usos es el de conseguir que cada uno de los representantes populares, en particular los integrantes de los poderes legislativos, representen a un número similar de ciudadanos. Sin embargo, ya que entre un censo y el siguiente su distribución espacial puede sufrir modificaciones importantes, el equilibrio entre los distritos electorales alcanzado después de un primer momento censal se verá alterado de maneras más o menos importantes en el siguiente. En consecuencia, se recurre a los resultados del censo más reciente para trazar nuevas fronteras entre distritos que permitan considerar que se ha restablecido el buscado equilibrio. Lo anterior puede conducir, en el caso de confederaciones de estados, a que alguno de ellos vea reducido el número de representantes que se le había asignado en el pasado reciente, en favor de alguno otro. Ésta es, sin duda, una de las consecuencias más importantes de los censos de población levantados en el 2010 en México (ver figura 1) y en otros países, la cual parece ser una de las razones más importantes por las que los recuentos poblacionales deben ser precisos y no exhibir sesgos de ningún carácter. Una consideración semejante parece haber conducido a la Suprema Corte de los Estados Unidos de América (EE.UU.) a dictaminar que su oficina de censos no podía llevar a cabo sus planes de reemplazar su censo decenal por una gran encuesta con diseño rotatorio.
Por lo que toca al segundo de los usos mencionados, se está frente a una de las situaciones aparentemente mejor definidas en cuanto al uso de esta información estadística. Por ejemplo, en México la Ley de Coordinación Fiscal vigente2 establece en su artículo segundo que el “Fondo General de Participaciones se constituirá con el 20% de la recaudación federal participable que obtenga la federación en un ejercicio (…) El Fondo General de Participaciones se distribuirá conforme a la fórmula siguiente:
![]() (1.1)
(1.1)
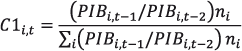 (1.2)
(1.2)
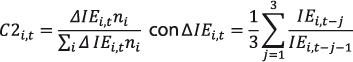 (1.3)
(1.3)
![]() (1.4)
(1.4)
donde: C1i,t , C2i,t , y C3i,t son los coeficientes de distribución del Fondo General de Participaciones de la entidad i en el año en que se efectúa el cálculo”.
A lo anterior sigue una definición precisa de cada uno de los elementos involucrados y que se refieren a la actividad económica (PIB), a la recaudación (IE) y al tamaño poblacional en cada entidad y en un momento dado. Destacamos la siguiente: “ni es la última información oficial de población que hubiere dado a conocer el Instituto Nacional de Estadística, Geografía e Informática [Sic.] para la entidad i“. Por supuesto, ésta es de nuevo una situación potencialmente conflictiva, pues la percepción de que un conteo censal a cargo del Instituto Nacional de Estadística y Geografía (INEGI) de México pudiese resultar en un decremento en el número de pobladores para alguna de las entidades, trae aparejada la certeza de que ello será causa de la recepción de una menor cantidad de recursos para las administraciones locales.
1.2 Necesidad de actualización constante de las cifras
El hecho de que las cifras poblacionales se actualicen a través de censos solamente cada cinco o 10 años tiene algunas implicaciones que podrían ser consideradas desfavorables por algunos. Entre las entidades federativas, las tasas de fecundidad y de mortalidad muestran diferencias que pueden llegar a ser grandes; asimismo, los movimientos migratorios que se dan entre ellas suelen favorecer a unas a costa de otras; por lo anterior, se tiene que los ritmos de crecimiento que muestran serán también diferentes. En consecuencia, si se decide mantener fijas las estructuras que reflejan la distribución espacial de la población en el territorio nacional a lo largo de todo un intervalo intercensal, aquellas entidades cuya población crece más rápidamente estarán recibiendo recursos inferiores que los que les corresponderían en razón al tamaño relativo de su población al paso de apenas uno o dos años. La evolución diferenciada de la distribución espacial al paso del tiempo hace necesaria una más frecuente actualización de dichas cifras para cada una de las entidades federativas que la que permiten los ejercicios censales en vista, por ejemplo, de que la distribución de recursos fiscales tiene lugar año con año.
La estrategia seguida por el INEGI en la publicación de cifras poblacionales absolutas para las encuestas que elabora entre censo y censo ha consistido en aprovechar estimaciones de los tamaños futuros de las subpoblaciones relevantes. Cabe señalar que dichas cifras han sido consideradas “la última información oficial de población” que hubiere dado a conocer el INEGI y, en consecuencia, usadas en la distribución de recursos fiscales a las entidades federativas. En particular, tales cifras se han basado, a su vez, en los ejercicios de proyección elaborados por el Consejo Nacional de Población (CONAPO) que, partiendo de los resultados históricos censales y muestrales, así como de la estadística (registros y encuestas) sobre hechos vitales, buscan producir las mejores aproximaciones del comportamiento que exhibirán los tamaños de las subpoblaciones durante el periodo intercensal inmediato y más allá. Tales estimaciones también son actualizadas cada cinco o 10 años, pero tienen la ventaja de presentar resultados para cada uno de los años de proyección.
Sin lugar a dudas, el supuesto más importante detrás de los ejercicios tradicionales de estimación consiste en que las tendencias de las tasas que explican la dinámica poblacional, así como sus proyecciones futuras, mostrarán un comportamiento suave. En general, la aplicación de los valores extrapolados de estas tasas a una población base dará lugar a una aproximación del comportamiento promedio que se observaría bajo esas condiciones. Ya que es claro que es difícil que una predicción coincida exactamente con el valor que será observado eventualmente, se plantean además comportamientos alternativos para las tasas futuras, a los que se denominan escenarios, y a partir de los cuales se obtienen estimaciones complementarias del comportamiento promedio. Es de esperarse que, salvo por la ocurrencia de eventos extraordinarios que modifiquen las tendencias observadas, los tamaños poblacionales futuros se encontrarán entre los promedios determinados por los escenarios más extremos. Por esta vía, sin embargo, resulta imposible hacer afirmaciones válidas sobre la precisión de las estimaciones obtenidas.
Peor aún, cuando tienen lugar eventos extraordinarios con efecto en la evolución de la población, pero que no pudieron ser previstos ni incorporados en las proyecciones, uno o más de los supuestos en que éstas se basaron no serán satisfechos. Ejemplo de estos eventos pueden ser las crisis bancarias iniciadas en México en 1995 o en los EE.UU. en el 2008, y cuyo impacto en las cifras de migración internacional entre ambos países es innegable aunque no se conozca de manera precisa. Es de esperarse que, bajo estas condiciones, el resultado de las proyecciones de población se aleje aún más del comportamiento que será observado, por ejemplo, a través de los censos de población.
En resumen, es necesario enfrentar el hecho de que, a pesar de la importancia de los usos administrativos y estadísticos de la información sobre el tamaño poblacional, los métodos propuestos y en uso para aproximar adecuadamente dicho tamaño muestran deficiencias que no resulta fácil corregir. En consecuencia, se hace necesario buscar alternativas para elaborar mejores aproximaciones para los tamaños futuros de la población.
1.3 Evolución reciente del tamaño de la población mexicana según los censos y las proyecciones elaboradas a partir de ellos
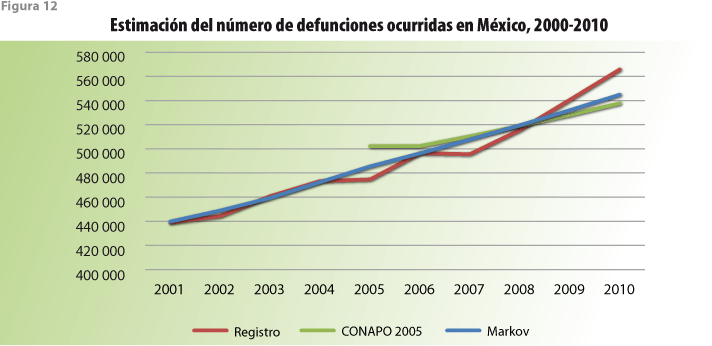
A lo largo de las dos décadas más recientes, México ha recolectado información con relación al tamaño de su población y la de cada una de las entidades federativas en cinco ocasiones haciendo uso de la técnica censal. Los cuadros 1 y 2, así como la figura 2, resumen esta experiencia para la población total del país. Entre 1990 y 1995, la población del país creció al ritmo de una tasa media anual de 2.06 por ciento. El censo levantado en el 2000 mostró que el ritmo de crecimiento medio anual para el quinquenio anterior se redujo a sólo 1.58 por ciento. Esta tendencia decreciente pareció encontrar confirmación con el resultado del conteo poblacional del 2005, cuyo resultado dio lugar a un crecimiento medio anual para el quinquenio inmediato anterior de sólo 1.02 por ciento. Ante el comportamiento anteriormente descrito se hace comprensible la sorpresa a que dio lugar el que, de acuerdo con el censo levantado en el 2010, la población del país haya crecido a un ritmo anual promedio de 1.85%, ritmo significativamente mayor que el inmediato anterior y también más grande que el experimentado entre 1995 y el 2000.
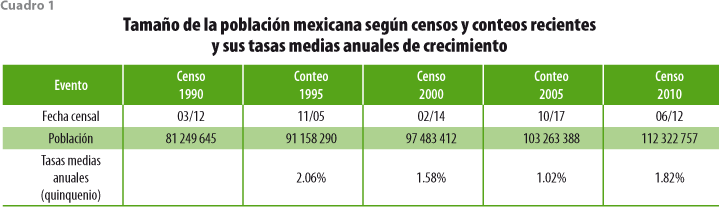
Es, asimismo, comprensible que las proyecciones poblacionales elaboradas por el CONAPO al final de cada uno de los quinquenios considerados muestren comportamientos futuros diferentes para el tamaño de la misma población. Así, de acuerdo con la figura 2, el ejercicio de proyección elaborado en 1995 extrapoló casi de manera natural la tendencia reciente de crecimiento, atenuándola paulatinamente hacia el mediano y largo plazos. A pesar del menor ritmo de crecimiento exhibido por el censo del 2000, el siguiente ejercicio de proyección parte de un valor poblacional más cercano al valor de la proyección elaborada cinco años antes que al exhibido por el mencionado censo; sin embargo, la proyección hacia el futuro consideró un crecimiento más lento que el contemplado en 1995. Aparentemente, la evidencia aportada por el conteo del 2005 dio lugar a una reconsideración importante sobre el punto inicial para la proyección poblacional elaborada inmediatamente después. Estoy seguro de que el resultado del censo llevado a cabo en el 2010 dio lugar también a una sorpresa importante en el CONAPO. Está claro que la tarea de elaborar proyecciones de población presenta retos importantes que las metodologías desarrolladas con ese fin no han podido resolver.
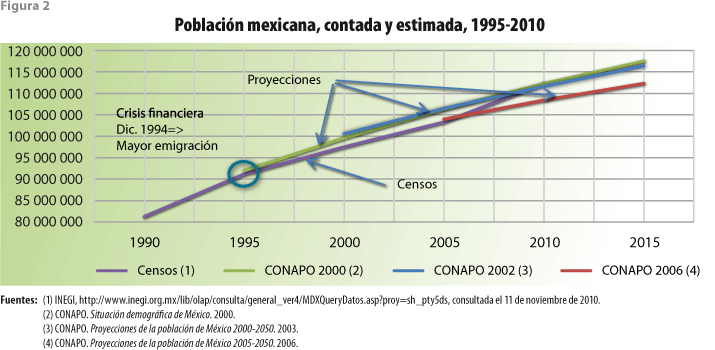
Cabe, por supuesto, preguntarse sobre lo que pudo haber causado un comportamiento como el observado: crecimiento acelerado-recesión-crecimiento acelerado. Por supuesto, el descenso en los valores de la tasa de fecundidad, consecuencia de políticas de población instrumentadas en las décadas inmediatas anteriores, ayuda a explicar, así sea parcialmente, la relación entre las primeras dos fases de crecimiento y de recesión. Cabe añadir, sin embargo, que durante el mismo periodo se alcanzan también reducciones en las tasas de mortalidad en el país, lo que atenuará el impacto de una menor fecundidad. Todo parece indicar que el comportamiento observado en el crecimiento de la población de México puede también ser parcialmente explicado por dos eventos semejantes, pero separados por casi un decenio y por la geografía. El conteo de 1995 fue levantado a casi un año de haberse iniciado una crisis financiera importante en el país. El sistema financiero nacional estuvo a punto de colapsar trayendo consecuencias sobre el resto de la economía y golpeando con particular importancia a la producción y al empleo. Es sabido que entre las consecuencias económicas y sociales de eventos catastróficos se encuentra la emigración hacia regiones o países que son percibidos como con mayor bienestar relativo. En general, los emigrantes se encuentran en el grupo de edades con capacidad para trabajar el cual, en muy buena medida, coincide con el que agrupa las edades reproductivas. En otras palabras, la población crecerá más lentamente no sólo a causa de la pérdida migratoria, sino de los nacimientos que no ocurrirán en el país a causa de la misma emigración. Algo semejante sucederá con las defunciones que no se registrarán en el país por haber ocurrido en otros lugares.
Es de esperarse que, al paso de la cresta de la crisis, una parte de los migrantes regrese a su lugar de origen, lo que atemperará la menor tasa de crecimiento de la población. Sin embargo, y en contraposición, los que hayan logrado establecerse en sus lugares de destino buscarán que sus familias emigren para reunírseles y, asimismo, procurarán compartir su buena fortuna atrayendo a hermanos, primos y sobrinos; nuevamente, nacimientos y defunciones en el sitio de origen serán menores a los esperados. Lo anterior, además, postergará la etapa de recuperación del crecimiento poblacional, la cual, cuando se dé, ocurrirá a un ritmo menor durante un periodo más o menos largo.
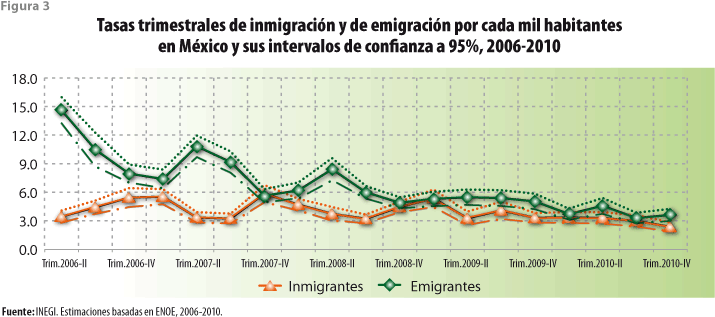
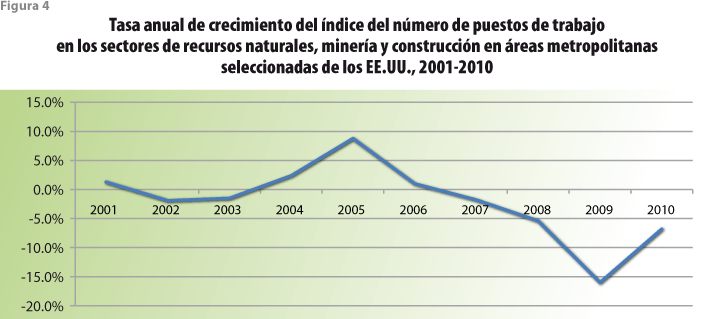
En ausencia de información precisa, podemos suponer que los mecanismos descritos en el párrafo anterior estuvieron en operación por algún tiempo durante la década 1995-2005. A partir de la información obtenida trimestralmente a través de la Encuesta Nacional de Ocupación y Empleo (ENOE), misma que empezó a recopilarse sólo a partir del 2006 y que se refiere a la modificación de la composición de los hogares en el país, se observa que la emigración desde México sufre una importante caída durante los primeros años de observación, para casi estabilizarse durante el periodo 2009-2011. Esta caída coincide en el tiempo con la mostrada por la tasa de crecimiento del número de puestos de trabajo en sectores en los que encuentran ocupación los migrantes mexicanos en los Estados Unidos de América, como es el de los recursos naturales, la minería y la construcción en ese país de acuerdo con el promedio elaborado a partir de la información para algunas áreas metropolitanas por Pittsburgh Today3 con datos de la Oficina de Estadísticas del Trabajo (BLS, por sus siglas en inglés) de ese país, según se muestra en la figura 4. Para casi todos los otros sectores, la crisis financiera sólo se dejó sentir hacia el 2008. En vista de lo anterior, se invierte la situación descrita párrafos arriba: la menor reducción en el número de personas en edades reproductivas da lugar a un número mayor de nacimientos aun cuando las tasas de fecundidad sigan descendiendo o se mantengan estables; el efecto sobre la mortalidad registrada es menor, ya que ésas son, precisamente, las edades en las que las tasas de mortalidad son relativamente pequeñas. De todo lo anterior se desprende una posible explicación para el mayor crecimiento del tamaño poblacional en México durante la década 2000-2010.
1.4 Aprovechamiento de las cifras futuras del tamaño de una población
En consecuencia, el INEGI debe ser doblemente cauto con la expansión de los resultados muestrales en los periodos intercensales. En particular, en lo que toca a la periodicidad, necesidades específicas del INEGI le llevan a producir estimaciones trimestrales a partir de los datos del CONAPO a través de rutinas de interpolación. Hasta ahora, eso es lo reportado al Congreso de la Unión y lo usado por la Secretaría de Hacienda y Crédito Público (SHCP) en las expresiones (1.2), (1.3) y (1.4), en cumplimiento de la Ley de Coordinación Fiscal. A nuestro juicio, lo anterior requiere ser revisado para incorporar la consideración de migraciones cíclicas intranuales, consecuencia de la realización de diversas actividades estacionales, tanto para los fines presupuestales expuestos como para otros propios del INEGI.4
1.5 Organización del trabajo
De la discusión anterior se desprende la importancia para las administraciones públicas y para la sociedad en su conjunto de disponer de estimaciones y proyecciones poblacionales de corto plazo de la mayor precisión posible. En la literatura es posible encontrar aplicaciones que, con este fin, recurren al uso de estructuras matriciales de diversa naturaleza y que consideran sólo de manera parcial las influencias más importantes de la dinámica demográfica. Una de las primeras referencias importantes en el tema puede ser encontrada en los trabajos pioneros de Leslie (1945) en los que se consideran exclusivamente la supervivencia y la fecundidad de las hembras de una población arbitraria, enfoque que sigue encontrando aplicación en trabajos recientemente publicados en revistas de Ecología. Andrei Rogers (1966) define matrices de crecimiento interregionales que incorporan a la migración neta, con lo que no se hace explícita la región de origen o la de destino de los migrantes, así como a las otras influencias principales de la dinámica demográfica, a partir de la adición de matrices más simples que modelan cada una de ellas, pero sin hacer distinción entre las poblaciones masculina y femenina. En México es posible encontrar también ejemplos de la aplicación de un enfoque markoviano a la evolución de poblaciones diversas, entre los que destacan los elaborados por Virgilio Partida (1989), los cuales, sin embargo —como en los casos anteriores—, ignoran una o más de las características importantes en las poblaciones humanas.
En el presente trabajo, partiendo de las semejanzas entre algunas estructuras básicas de la demografía y las de las Cadenas de Markov, se busca superar las limitaciones señaladas para las anteriores propuestas. Para ello, y con el fin de lograr una contabilidad demográfica precisa, desde la forma más básica del modelo se hace el planteamiento completo de la matriz que modela a la dinámica demográfica al incluir explícitamente a aquellos estados identificados con el fallecimiento a una edad determinada. En general, esta submatriz es irrelevante para la proyección hacia el futuro de las estructuras por edad, sexo y región de una población; sin embargo, para aplicaciones como la retroproyección de poblaciones entre, digamos, dos censos sucesivos como parte de un ejercicio amplio de conciliación demográfica es necesario establecerla en su totalidad. Con el fin de evitar un doble conteo de individuos que, por ejemplo, emigran y fallecen en el mismo periodo, el modelo que se presenta combina las matrices de influencias demográficas a través de los productos adecuados de las matrices que se asocian a cada una de ellas en lugar de su mera adición, como ocurre en la propuesta de Rogers (1966). El modelo propuesto hace, además, una consideración explícita de ambos sexos y de todas las edades desplegadas en las poblaciones de cada una de las regiones consideradas en el estudio, en contraposición a los enfoques de Rogers (1966) y Partida (1989). Asimismo, la versión final considerada en este trabajo incluye, para cada región considerada y para cada sexo, submatrices de tasas anuales de emigración hacia cada uno de los destinos lo que hace posible determinar los saldos migratorios para cada par de regiones. Al contribuir con ello a la ya aludida precisión en la contabilidad demográfica, se sigue de mejor manera la evolución de los tamaños relativos de las poblaciones de las regiones consideradas, permitiendo con esto cumplir también de mejor manera los principios de equidad detrás de los planteamientos de, por ejemplo, la Ley de Coordinación Fiscal mexicana.
Este enfoque general permite, además, la imposición de restricciones sobre los comportamientos esperados de modo que sus resultados las tomen en cuenta. Lo anterior se ejemplifica de manera numérica en este trabajo aplicando el modelo propuesto e imponiendo un número relativamente pequeño de restricciones sobre la evolución de la población de México en la década 2000-2010, que se refieren a la coincidencia entre los resultados anuales del modelo y los cuatro totales nacionales (sin distinción ni de sexo, ni de edad, ni de entidad federativa) que año con año publica el INEGI para los nacimientos y las defunciones, así como las estimaciones del número de emigrantes y del de inmigrantes obtenidos de diversas fuentes. En total, para cada uno de los años de proyección, el modelo estima el tamaño de las subpoblaciones definidas por cada una de las combinaciones de entidad federativa, sexo y grupo quinquenal de edad, totalizando alrededor de 1 280 valores. Para ello, se parte de las estructuras poblacionales determinadas para el año anterior, de las matrices de tasas por hecho, edad, sexo y región, así como mediante la imposición de las cuatro (4) restricciones señaladas. En otras palabras, y aunque fue necesario realizar algunas extrapolaciones para los últimos años del periodo, algo parecido a una rudimentaria conciliación continua tuvo lugar para llegar a las estimaciones markovianas; rudimentaria, porque no se hizo uso de toda la información estadística publicada para esta década por entidad federativa, sexo y edad. Tales estimaciones son comparadas con las obtenidas mediante métodos de proyección usados por el CONAPO a partir del 2000 y para cada uno de los años del periodo, así como las que resultan del censo levantado por el INEGI en el 2010. Para este último año, en términos de los tamaños absolutos de cada una de las subpoblaciones disponibles, se alcanzó una importante coincidencia entre las estimaciones censales y markovianas. Bajo el supuesto de que la consideración de los tamaños relativos de cada una de dichas subpoblaciones acercaría las estimaciones elaboradas por el CONAPO se realizó una nueva comparación, pero con resultados semejantes a los anteriores.
Lo anterior nos lleva a concluir que las proyecciones del CONAPO fallan no sólo en lo que toca a los tamaños poblacionales absolutos, discrepancias causadas tal vez por efectos exógenos, como crisis económicas en los países de origen o destino de los migrantes y que son difíciles de incorporar a cualquier ejercicio de proyección, sino también en una consideración adecuada de los impactos migratorios interestatales e internacionales por lo que las estructuras relativas que ellas reflejan dejan pronto de tener vigencia.
El trabajo está organizado de la siguiente manera. En la sección Aplicación a la demografía, después de comentar las estructuras primigenias de la demografía denominadas tablas de vida, se establecerá su representación como matrices de transición.5 Del mismo modo, las estructuras por edad de una población serán rescritas en términos de las probabilidades absolutas de las Cadenas de Markov. La primera aproximación a la evolución de una población por efecto de la mortalidad será gradualmente complementada para incluir la consideración de los efectos de la migración tanto interna como internacional. Se mostrará cómo la modelación lograda hasta ese momento puede ser extendida a la consideración de estructuras por edad y sexo. De este modo se estará en condiciones de incluir en el modelo los efectos de la fecundidad.
La sección Aplicación a la demografía puede ser considerada muy técnica por algunos lectores por lo que, en ese caso, sugiero que procedan directamente a la sección Prueba de estrés del modelo en la que, a manera de ejemplificación, se muestra la aplicación del modelo a las cifras censales mexicanas, partiendo de la cifra poblacional del 2000, con base en la estadística obtenida de los registros de nacimientos y defunciones para el decenio, así como en diversas encuestas levantadas en México y en los EE.UU. en el mismo decenio, se llega a la estimación del tamaño de la población mexicana y el de cada una de sus entidades para febrero del 2010.
2. Aplicación a la demografía
En la exposición subsecuente se seguirá un enfoque incremental con el propósito de explicitar la relación entre las más importantes influencias de la dinámica poblacional con las estructuras de las Cadenas de Markov. En primer lugar se tratará la mortalidad por ser la sobrevivencia el fenómeno demográfico más claramente markoviano.6 Se modelará inicialmente la evolución de una cohorte para después proceder a considerar la evolución simultánea de varias cohortes. Posteriormente, la modelación de la migración permitirá considerar tanto ingresos al grupo a distintas edades, por inmigración, como salidas del mismo por razones diferentes a la mortalidad. En el estudio de la migración se considerarán la interestatal y la de carácter internacional. Enseguida, se añadirá la consideración de las posibles diferencias entre los sexos tanto por lo que se refiere a la mortalidad como a la migración. Por último, se incorporarán los ingresos a cada una de las subpoblaciones por fecundidad por supuesto distinguiéndolos por sexo del recién nacido.
2.1 Tablas de vida y su expresión como matrices de transición
El modelo detrás de la construcción de una tabla de vida, también conocida como de mortalidad, supone el seguimiento de un grupo numeroso de individuos nacidos simultáneamente, denominado cohorte. Se modela la evolución anual del tamaño del grupo hasta su extinción ya que no se consideran nuevos ingresos al mismo por ninguna vía. De este modo l0 denota al tamaño inicial de la población, conocido como rádix. Similarmente, lx denota a los que alcanzan vivos la edad x y dx a los que, habiendo llegado vivos a la edad x, fallecen antes de su siguiente cumpleaños. Así, debe tenerse que de entre los que alcanzaron vivos la edad x algunos sobrevivirán hasta la edad x + 1 y el resto fallecerá antes de que esto ocurra; más precisamente, debe tenerse que lx = lx+1+ dx. Se denotará por ω a la primera edad tal que lx = 0; es decir, a la menor edad que ninguno de los miembros de la cohorte alcanza vivo.
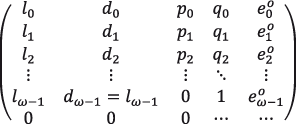 (2.1)
(2.1)
Las columnas p y q presentan las probabilidades de sobrevivencia a la siguiente edad y de fallecimiento en el momento de cumplir la edad x, respectivamente. Sus valores se definen como en (2.2) y en (2.3).
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
La columna e0 presenta al número promedio de años que le quedan por vivir a una persona de edad x; se conoce como la “esperanza de vida a edad x“. Sus entradas se calculan como en (2.4).
![]() (2.4)
(2.4)
La probabilidad px se interpreta como una probabilidad de transición (ver A.17) entre el estado “vivo a la edad x ” y el estado “vivo a la edad x +1″; en tanto que su complemento qx se refiere a la transición entre el estado “vivo a la edad x” y “muerto antes de cumplir la edad x +1″. De este modo,
![]() (2.5)
(2.5)
y
![]() (2.6)
(2.6)
De otro modo, si T denota a la variable aleatoria “tiempo hasta el fallecimiento” para una persona seleccionada al azar de la población, debe tenerse que:
![]() (2.7)
(2.7)
Debe señalarse que existe una diferencia conceptual, sin embargo, entre estas probabilidades al instante en el que cumplen la edad x y las que han sido definidas para ser usadas en el contexto markoviano, al inicio de un periodo o al instante t. Los cumpleaños ocurren a lo largo de todo el año por lo que afirmaciones tales como “vivos de edad x en el instante t” se refieren a quienes alcanzaron esa edad recientemente, dejando fuera a quienes la alcanzarán a lo largo del periodo (t, t+1]. A pesar de ello, y en vista de las semejanzas señaladas y de que numéricamente no hay grandes diferencias, con fines de exposición y de cálculo de las ejemplificaciones las usaremos como probabilidades de transición al instante t. Por supuesto, el lector podrá decidir usar otras definiciones, por ejemplo, la tasa media o central de mortalidad si sólo le interesa el punto central del año. Ello, sin embargo, no cambiará en modo alguno la exposición subsecuente.
En consecuencia, se rescribirá lo anterior en notación markoviana. Para la supervivencia, se tiene un primer conjunto de estados, los designados por una “l“, que equivalen a las edades que los individuos pueden alcanzar en vida; en este caso, dicho conjunto queda representado por E = {l0,l1,…,lω-1}. Por su parte, el conjunto D = {d0,d1,…,dω-1} identifica a los estados relacionados con el fallecimiento a una edad determinada, los cuales se ubican tanto en la segunda mitad de los renglones como en la de las columnas. Éstos son estados diferentes de los demás ya que cuando el proceso entra a uno de ellos, con probabilidad igual a 1 (i.e., con certeza) ya no lo abandona. Por esta razón, en la terminología de las Cadenas de Markov, se les denomina absorbentes.
De este modo, en (2.8) se presenta la matriz de transiciones (ver A.2) que será denotada por M y cuya dimensión es (2ω) × (2ω).
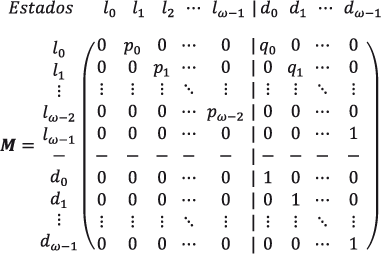 (2.8)
(2.8)
Para estudiar la supervivencia, conviene escribir a la matriz M definida en (2.8) en bloques matriciales y notación obvia como:
![]() (2.9)
(2.9)
En vista de que la suma de los valores en los renglones de la matriz M es igual a 1, se tiene que las submatrices L y D, que son diagonales, están relacionadas como se indica en (2.10).
![]() (2.10)
(2.10)
donde las entradas de la matriz J son todas iguales a cero excepto por las de la primera diagonal superior, que toman el valor 1. El efecto de posmultiplicar una matriz diagonal por J es el de trasladar los valores en la diagonal principal un lugar a la derecha hasta la primera diagonal superior. En el presente contexto, esa operación aritmética coloca las tasas anuales de supervivencia para cada edad en la posición correcta para modelar transiciones desde la x hasta la x + 1.
De este modo es fácil ver que, en concordancia con las expresiones (A.5) y (A.6) y bajo el supuesto de estacionariedad, las probabilidades de que un individuo que llegó vivo a la edad x sobreviva dos o más periodos o fallezca antes del transcurso de los mismos, no son otra cosa que las entradas en el renglón x de la potencia correspondiente de la anterior matriz, como se muestra a continuación:
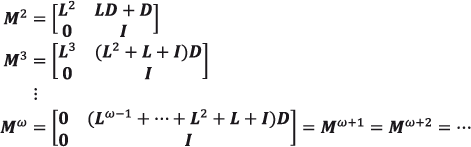
El bloque superior derecho en cada una de las anteriores matrices resume las probabilidades de fallecer antes de que transcurran dos, tres u ω años, respectivamente. Más aún, para un grupo cerrado, como el que ha sido considerado hasta ahora, la extinción está garantizada como puede verse a partir de los valores que toman las submatrices superiores izquierdas, todas cuyas entradas eventualmente toman el valor cero; es decir, la probabilidad de sobrevivir más allá de la edad ω es idénticamente cero, tal como estaba previsto.
Aun en presencia de probabilidades de muerte que cambian con el paso del tiempo, se tendría un comportamiento semejante. En otras palabras, el grupo acabaría por extinguirse y las probabilidades de no sobrevivir uno, dos, tres o más periodos quedarían dadas por las matrices superiores derechas de las anteriores expresiones. En efecto, considere la sucesión {Mt+j, j ≥ 0} definida según la expresión (2.11),
![]() (2.11)
(2.11)
donde Li modela la supervivencia en el año i y t es el primer año del periodo bajo consideración. La mortalidad es entonces modelada por productos de matrices sucesivas en la secuencia (2.11) en lugar de las potencias de la versión estacionaria. En efecto, los productos de la forma Lj D serían remplazados por productos de la forma ![]() . En general, se tiene entonces que los productos de las matrices {Mt+j} toman la forma:
. En general, se tiene entonces que los productos de las matrices {Mt+j} toman la forma:
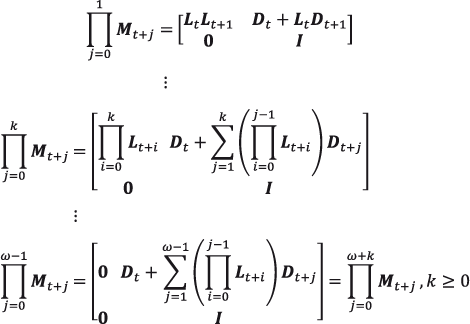
en una directa generalización de las versiones estacionarias.8
2.2 Estructuras por edad
Para una cohorte no tiene mucho sentido preguntarse por las estructuras por edad ya que, al final de cada año, todos los individuos que permanecen en la población tienen la misma edad. En la práctica se tiene que al inicio de nuestra observación hay individuos de todas las edades. Si denotamos por ![]() al número de personas de edad x = 0, , ω – 1 en la población en el periodo r, cada una de ellas puede ser conceptualizada como una realización independiente del proceso, sujeta a idénticas condiciones de sobrevivencia. En cada fecha censal, estos números serán conocidos con razonable precisión y se encuentran, junto con el tamaño total de la población
al número de personas de edad x = 0, , ω – 1 en la población en el periodo r, cada una de ellas puede ser conceptualizada como una realización independiente del proceso, sujeta a idénticas condiciones de sobrevivencia. En cada fecha censal, estos números serán conocidos con razonable precisión y se encuentran, junto con el tamaño total de la población ![]() , entre la información más importante en la cual basar una buena parte de la planeación y seguimiento de políticas públicas de educación, empleo, pensiones o salud, por mencionar sólo algunos ejemplos.
, entre la información más importante en la cual basar una buena parte de la planeación y seguimiento de políticas públicas de educación, empleo, pensiones o salud, por mencionar sólo algunos ejemplos.
Con base en dichos tamaños podemos definir la proporción en que están presentes en la población los individuos de cada grupo de edad y que está dada por (2.12).
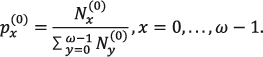 (2.12)
(2.12)
Por lo anterior, (2.12) puede interpretarse como la probabilidad de que la edad de una persona, elegida al azar de entre los integrantes de la población en el momento censal, sea igual a x; en otras palabras, que Pr(X0 = x), x = 0,…, ω – 1.
En los periodos intercensales, en ausencia de un registro preciso de los pobladores de un país o región, dichas proporciones habrán de ser estimadas por otra vía. Es fácil ver que sus proyecciones para el primero de los periodos futuros pueden ser obtenidas como se muestra en (2.13).
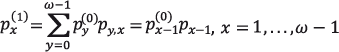 (2.13)
(2.13)
La segunda igualdad es obvia ya que en el transcurso de un periodo sólo es posible alcanzar la edad x desde la x – 1. Por supuesto, en ausencia de hipótesis sobre la fecundidad a ser tratada más adelante, debe tenerse que para la edad x = 0,![]() = 0. En general, estas expresiones pueden mostrarse de manera resumida en notación matricial como en (2.14), donde
= 0. En general, estas expresiones pueden mostrarse de manera resumida en notación matricial como en (2.14), donde ![]() t es el vector columna de dimensión ω cuyas entradas son las probabilidades
t es el vector columna de dimensión ω cuyas entradas son las probabilidades ![]() para las edades x = 0,1, … , ω – 1.
para las edades x = 0,1, … , ω – 1.
![]() (2.14)
(2.14)
La semejanza entre (2.14) con (4.10) debe ser destacada. En general, debe tenerse que:
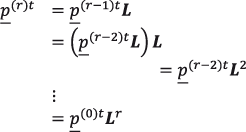 (2.15)
(2.15)
Cabe señalar que el tamaño de cada grupo de edad al final de cada periodo puede ser estimado como ![]() . A causa de las defunciones ocurridas a lo largo del tiempo debe tenerse que el tamaño actual de la población debe ser menor que el original; es decir, que
. A causa de las defunciones ocurridas a lo largo del tiempo debe tenerse que el tamaño actual de la población debe ser menor que el original; es decir, que ![]() , lo que se explica a su vez porque
, lo que se explica a su vez porque ![]() . Lo anterior se debe a que el vector de probabilidades absolutas
. Lo anterior se debe a que el vector de probabilidades absolutas ![]() no considera a todos los estados de la cadena, incluidos los absorbentes. Es decir, hace falta un segundo vector que lo complemente, al cual puede denotarse por
no considera a todos los estados de la cadena, incluidos los absorbentes. Es decir, hace falta un segundo vector que lo complemente, al cual puede denotarse por ![]() (r), cuya función dentro de iteraciones como (2.15) en las que se hace uso de la matriz completa de transiciones M es la de llevar contabilidad del número acumulado de defunciones ocurridas en cada edad a lo largo de varios periodos:
(r), cuya función dentro de iteraciones como (2.15) en las que se hace uso de la matriz completa de transiciones M es la de llevar contabilidad del número acumulado de defunciones ocurridas en cada edad a lo largo de varios periodos: ![]() ; en otras palabras, las muertes recientes más las ocurridas en el pasado.
; en otras palabras, las muertes recientes más las ocurridas en el pasado.
En general, y en vista de la presión que ejercen sobre todo tipo de recursos, la planeación del desarrollo hace un mayor énfasis en el tamaño presente y futuro de los sobrevivientes por lo que en adelante concentraremos nuestra atención en el vector ![]() , salvo indicación en contrario. Por supuesto, bajo las actuales circunstancias, debe tenerse que el grupo irá extinguiéndose ya que
, salvo indicación en contrario. Por supuesto, bajo las actuales circunstancias, debe tenerse que el grupo irá extinguiéndose ya que ![]() para las edades x = 0,…, r – 1 siempre que r ≥ 1. Ello se debe a que para modelar la evolución del grupo no se han incorporado supuestos ni de fecundidad ni de migración.
para las edades x = 0,…, r – 1 siempre que r ≥ 1. Ello se debe a que para modelar la evolución del grupo no se han incorporado supuestos ni de fecundidad ni de migración.
2.3 Migración
Para fijar ideas, considere una situación birregional. La emigración desde la región i hacia la j puede ser incorporada al modelo considerando una nueva matriz diagonal de tasas anuales de emigración por edad, la cual será denotada por Eij. De este modo, la permanencia en la región i hasta la siguiente edad será modelada por matrices ![]() dadas por (2.16), que indica que sólo quienes ni emigran ni fallecen alcanzan su siguiente cumpleaños como residentes en dicha región.
dadas por (2.16), que indica que sólo quienes ni emigran ni fallecen alcanzan su siguiente cumpleaños como residentes en dicha región.
![]() (2.16)
(2.16)
Por su lado, una segunda parte de los residentes originales en i alcanzará también vivo la siguiente edad, pero lo hará en la región j; en este caso, las tasas correspondientes se organizan en una matriz como la que aparece en (2.17). Correspondientemente, habrá individuos provenientes de j que se añaden a los residentes en i y que sobreviven hasta su siguiente cumpleaños; las tasas que denotan este hecho se encuentran en la matriz ![]() también definida por (2.17).
también definida por (2.17).
![]() (2.17)
(2.17)
Por último, se tendrá a quienes fallecen antes de cumplir un año más de edad. En este caso, se presentan dos posibilidades: están quienes fallecen sin haber emigrado, lo que se registra en (2.18); también, quienes fallecen después de haber inmigrado o emigrado por lo que su deceso ocurre en un lugar diferente del que se encontraban al inicio del periodo, y en el que se registra el hecho. Esta posibilidad queda dada por la matriz incluida en (2.19).
![]() (2.18)
(2.18)
![]() (2.19)
(2.19)
Con base en lo anterior, es posible redefinir a la matriz M, de dimensión (4ω) × (4ω), que modela tanto la supervivencia como la migración entre dos regiones, como en (2.20).
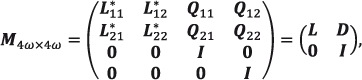 (2.20)
(2.20)
redefiniendo las matrices L y D. Los renglones de M vuelven a sumar a 1, ya que se enumera a la totalidad de los eventos posibles que puede enfrentar un individuo de la población ampliada a lo largo de un año. Una vez ocurrido un cambio de residencia a otra región, el modelo markoviano olvida este hecho y, para periodos subsecuentes, trata a los inmigrantes como a cualquier individuo nacido en la región de destino. En otras palabras, les aplica las mismas tasas de mortalidad, fecundidad, etcétera.
La extensión de (2.20) al caso en que se consideran tres o más regiones es inmediata. Por ejemplo, al considerar 32 entidades federativas y un estado adicional identificado como el resto del mundo (R), la gran matriz de transiciones M, ahora de dimensión (2 * 33 * ω × 2 * 33 * ω), queda redefinida en (2.21), donde se le presenta en bloques matriciales.
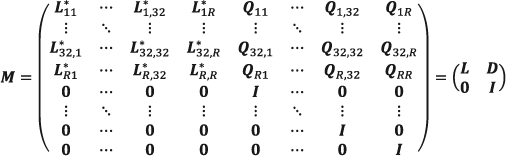 (2.21)
(2.21)
donde las matrices L y D han sido redefinidas nuevamente de manera obvia.
Una consecuencia importante de la expresión (2.21), que será demostrada más adelante (ver sección Ecuación compensadora, adelante), es que los saldos migratorios internos se saldan a nivel nacional. En otras palabras, el crecimiento de la población total de un país por desplazamientos de personas dentro de su territorio es cero, como es de esperarse. Ahora bien, aunque la matriz M definida en la expresión (2.21) tiene como fin principal modelar la evolución del tamaño y de las estructuras por edad y por regiones o estados de la población de un país conformado por un cierto número de divisiones políticas (32 entidades federativas en el ejemplo), la consideración del flujo de migrantes internacionales desde y hacia el país obligaría estrictamente a considerar asimismo la modelación de la evolución del tamaño y de la estructura por edades de la región R (resto del mundo), lo que puede resultar complicado. De forma alternativa, es posible considerar la adición de sobretasas (posiblemente negativas) por migración neta internacional ” desde i hacia el éter, o viceversa” en las matrices E que modelan la migración interna; su expresión podría ser del tipo “tantos emigrantes internacionales por cada emigrante interno”. Ello cancela la necesidad de considerar una región adicional, pero impide la identificación de la procedencia o destino de los migrantes internacionales lo que, en consecuencia, conduce a un saldo migratorio no nulo a nivel de país. Bajo las anteriores condiciones, la suma de los elementos en cada renglón de la matriz M puede ser diferente de 1. En algunos casos, el valor de esta suma es menor a 1 y el tamaño de la población decrece por exhibir un saldo migratorio negativo, lo que aceleraría su extinción; cuando el valor de dicha suma excede a 1, el tamaño poblacional crecería a costa del de otras entidades federativas o por inmigración internacional.
Aun en caso de considerar a todos los países o regiones del planeta, de acuerdo con el modelo, la población ampliada sigue siendo cerrada, por lo que de nuevo su extinción se dará con certeza, lo cual ya no resulta tan obvio. Sólo la consideración de la fecundidad evitará ese destino, ya que (aún) no existe registro de migración desde y hacia la Tierra.
2.4 Estructura por edad y sexo
Los elementos y las expresiones presentadas hasta ahora son susceptibles de ser extendidas para considerar comportamientos diferentes entre sexos en cuanto a mortalidad y a migración. Para este fin, se modelará la evolución diferencial por edad y sexo reordenando y agrupando, según sea necesario, a las submatrices que forman parte de las específicas de transición para cada sexo. En efecto, sean MF y MM las matrices que modelan la dinámica demográfica de las cohortes femeninas y masculinas que conviven en un momento dado, respectivamente, y cuya estructura es idéntica a (2.21) distinguiéndose tan sólo por los valores de las tasas anuales de mortalidad y de migración para mujeres y hombres. La expresión (2.22) redefine a la matriz M, el número de cuyos renglones y columnas alcanza ahora 2 × R × ω × 2 (= Sexos × Regiones × Edades × Permanencia o no), que resume la modelación del comportamiento de las dos influencias anteriores.
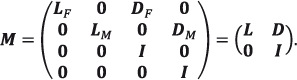 (2.22)
(2.22)
Por su parte, la distribución inicial por edades puede también presentarse en su versión por sexo y por región. Para ello, primero, se conjuntan las distribuciones iniciales femeninas por edad y región, así como las correspondientes masculinas, según (2.23) y (2.24), respectivamente.
![]() (2.23)
(2.23)
![]() (2.24)
(2.24)
Éstas, al ser consideradas de manera agregada, llevan a la distribución inicial por edad, sexo y entidad federativa ![]() definida como se muestra en (2.25).
definida como se muestra en (2.25).
![]() (2.25)
(2.25)
A partir de las definiciones anteriores se arriba a la proyección de las estructuras por edad y sexo, un periodo adelante:
![]() (2.26)
(2.26)
y, en general, r periodos adelante según (2.27).
![]() (2.27)
(2.27)
Aunque (2.27) hace explícito que se está considerando la proyección de la población de cada sexo por separado (lo que podría conducir a la generalización a tres o más sexos), hace también evidente que las formas recursivas básicas (2.14) o (2.15) para el cálculo de proyecciones se extienden naturalmente a este caso, con la misma aparente simplicidad a pesar de tratarse ahora de la modelación de una situación considerablemente más compleja que la considerada en aquéllas.
2.5 Fertilidad
A partir de tasas anuales de fertilidad específicas por edad de la madre ![]() , es posible añadir a nuestro modelo el ingreso de nuevos individuos. En una primera aproximación, para el primer periodo de observación y para una región i cualquiera, el número de recién nacidos al final del mismo periodo podría calcularse como se indica en (2.28).9
, es posible añadir a nuestro modelo el ingreso de nuevos individuos. En una primera aproximación, para el primer periodo de observación y para una región i cualquiera, el número de recién nacidos al final del mismo periodo podría calcularse como se indica en (2.28).9
![]() (2.28)
(2.28)
Sin embargo, (2.28) puede conducir a una sobrestimación del número de nacimientos pues considera que todas las mujeres en edad fértil presentes en una región determinada al inicio de un periodo, incluidas las que fallecerán o emigrarán a lo largo del mismo, estarán expuestas al riesgo de dar a luz durante su total duración y en la misma región. En algunos casos reportados en la literatura se ha intentado incorporar en (2.28) el efecto de la mortalidad, pero no conozco ninguno en que se haga algo similar para el de la migración. Por otro lado, de manera natural, tanto los alumbramientos como los decesos y las migraciones tienen lugar de manera continua y simultánea a lo largo de cada uno de los periodos. El modelo que hemos seguido hasta ahora, sin embargo, fija nuestra atención sólo en los instantes inicial y final de cada periodo. Es por ello que, con el fin de mantenernos en este contexto, será necesario llevar a cabo adaptaciones adicionales. Así, tanto para corregir la fertilidad por mortalidad y migración de las mujeres en edad fértil como para adaptarlos al modelo, será preciso hacer algunos supuestos simplificadores que nos permitan su modelado de manera simple, pero precisa.
La base del enfoque a seguir requiere que se simplifique la manera en que se modela la ocurrencia de los distintos eventos a lo largo del tiempo. Para ello, se supondrá que todos los alumbramientos tienen lugar simultáneamente en el instante central del periodo de modo que las mujeres expuestas al riesgo de parto en una región serán las que estén presentes en ese lugar en el mismo instante. Para la determinación de ese número, se recurrirá al supuesto de que defunciones y migraciones se distribuyen de manera uniforme a lo largo del periodo. En consecuencia, la frase “presentes en el instante central” incluye a aquellas presentes en la región al principio del periodo que en el instante central del mismo ni han muerto ni han emigrado. Incluye, asimismo, a las que habiendo inmigrado hasta ese momento no han fallecido. Por supuesto, excluye a las que hasta ese momento han emigrado y a las que ya fallecieron.
De este modo, la desagregación de la totalidad de las mujeres al inicio del periodo en cuatro categorías puede ser resumida como se muestra en el cuadro 2. La matriz (I – ½E)(I – ½D) aporta las tasas para el cálculo de aquellas que, estando presentes al principio del periodo, ni han emigrado ni han fallecido a mitad del mismo. Por su parte, ½E (I – ½D) lleva al cálculo de aquellas que, habiendo emigrado, no han fallecido. El segundo renglón muestra las matrices de tasas asociadas con las mujeres que han fallecido, tanto si emigraron, (I – ½E)½D, como si no, ½E½D. La suma de las dos matrices en el primer renglón debe llevar a la de tasas de sobrevivencia a mitad del periodo, (I – ½D); la de las del segundo renglón es igual a ½D y la de ambos totales es igual a I, es decir, al total de mujeres presentes al principio del periodo. Cuando la suma tiene lugar a lo largo de cada una de las dos columnas se tiene el mismo caso. En otras palabras, la población inicial es dividida en cuatro grupos exhaustivos y excluyentes. Por supuesto, bajo las condiciones establecidas sólo las mujeres sobrevivientes están en condiciones de reproducirse. Las que no han emigrado y dan a luz lo harán en su lugar de origen, en tanto que aquellas que tienen un parto de entre las que emigraron, lo harán en su lugar de destino.

Por lo que toca a las tasas de fertilidad aplicables se supondrá para las mujeres migrantes, por lo menos durante el periodo inmediato posterior al de su migración, que se les aplican las de su entidad de origen. De este modo, y con base en los supuestos anteriores, se debe tener que la fertilidad ![]() , corregida por mortalidad y por migración a la entidad j desde la i, queda dada según la expresión (2.29).
, corregida por mortalidad y por migración a la entidad j desde la i, queda dada según la expresión (2.29).
![]() (2.29)
(2.29)
Por su parte, la fertilidad en la región i, ![]() , corregida por mortalidad y migración, queda definida según (2.30).
, corregida por mortalidad y migración, queda definida según (2.30).
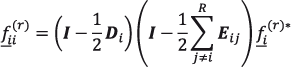 (2.30)
(2.30)
Estas tasas corregidas son tales que, para la región i,
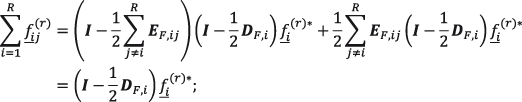
es decir, cuando se ignora la migración lo que aplica son tasas de fertilidad sólo corregidas por mortalidad.
Finalmente, se tiene que el número de recién nacidos en la i-ésima región al final del r-ésimo periodo puede ser expresado como se muestra en (2.31).
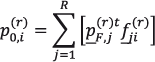 (2.31)
(2.31)
Debe ser claro que la expresión (2.31) no es otra cosa que el producto del vector ![]() , definido en (2.27), con el formado por la yuxtaposición de los de las tasas de fertilidad regionales, corregidas por mortalidad y migración. De este modo, cuando no interesa distinguir el sexo de los nacimientos, podemos modificar a cada una de las matrices
, definido en (2.27), con el formado por la yuxtaposición de los de las tasas de fertilidad regionales, corregidas por mortalidad y migración. De este modo, cuando no interesa distinguir el sexo de los nacimientos, podemos modificar a cada una de las matrices ![]() , definidas en (2.16), (2.17), (2.18) y (2.19), remplazando su primera columna por (2.29) o (2.30), según corresponda.
, definidas en (2.16), (2.17), (2.18) y (2.19), remplazando su primera columna por (2.29) o (2.30), según corresponda.
En general, por supuesto es útil distinguir el sexo de los recién nacidos. Para ello, se definen nuevas matrices LM,ij =![]() y LF,ij dada por (2.32), cuya semejanza con una matriz de Leslie es sólo aparente, pues la nueva matriz contempla además de la mortalidad a la emigración en
y LF,ij dada por (2.32), cuya semejanza con una matriz de Leslie es sólo aparente, pues la nueva matriz contempla además de la mortalidad a la emigración en ![]() . El segundo sumando en esa expresión es una matriz que tiene todas sus entradas iguales a cero excepto por las de su primer columna, la cual contiene al vector de tasas específicas de fertilidad por edad de la madre, corregidas por mortalidad y migración según (2.29) y (2.30); por su parte, el coeficiente α representa a la proporción de nacimientos femeninos.
. El segundo sumando en esa expresión es una matriz que tiene todas sus entradas iguales a cero excepto por las de su primer columna, la cual contiene al vector de tasas específicas de fertilidad por edad de la madre, corregidas por mortalidad y migración según (2.29) y (2.30); por su parte, el coeficiente α representa a la proporción de nacimientos femeninos.
![]() (2.32)
(2.32)
Del mismo modo se define la matriz Bij, relacionada con los alumbramientos masculinos, según (2.33).
![]() (2.33)
(2.33)
Por último, la versión completa del modelo markoviano estacionario, que considera mortalidad, fertilidad y migración para cada combinación de edad, sexo y región, quedaría dada nuevamente por (2.34).
![]() (2.34)
(2.34)
donde la matriz LT tiene la forma (2.35), para el caso en que se consideran R regiones.
 (2.35)
(2.35)
en notación obvia.
Destacamos que, bajo estas condiciones, se introduce una causa adicional por la que los renglones de la matriz (2.35) pueden no sumar a 1. Ello conducirá a cambios en el tamaño de la población usualmente aludidos como “crecimiento natural”, que no es sino la diferencia entre nacimientos y defunciones.
La forma de la expresión para actualizar las estructuras poblacionales por región, edad y sexo no se verá afectada a pesar de la incorporación del efecto por fertilidad. En su versión estacionaria aparece en (2.36).
![]() (2.36)
(2.36)
La versión no estacionaria se muestra en (2.37).
![]() (2.37)
(2.37)
2.6 Ecuación compensadora
Explicitando el álgebra que resumen tanto (2.36) como (2.37), y denotando por ![]() a un vector columna de dimensión ω cuyas componentes son todas iguales a 1, se tiene que, para la entidad i al final del periodo t + 1, el tamaño poblacional Pi(t+1) es calculado como en (2.38).
a un vector columna de dimensión ω cuyas componentes son todas iguales a 1, se tiene que, para la entidad i al final del periodo t + 1, el tamaño poblacional Pi(t+1) es calculado como en (2.38).
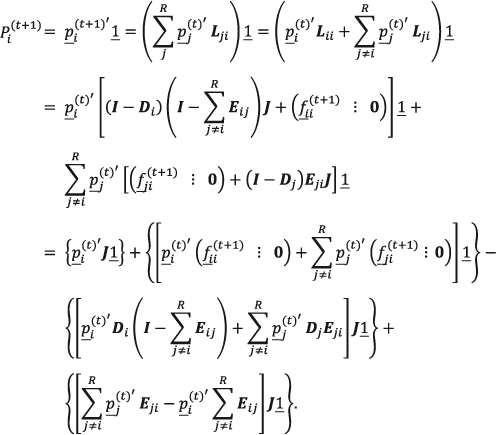 (2.38)
(2.38)
Abusando un poco de la notación, ya que la fertilidad está relacionada sólo con las estructuras femeninas por edad. En (2.38) bastará con suponer que los valores de las tasas de fecundidad en la porción correspondiente a la población masculina, en las versiones extendidas de cada uno de los vectores ![]() , son idénticamente iguales a cero.
, son idénticamente iguales a cero.
Los términos de la expresión en (2.38) han sido ordenados para hacerlos coincidir con la forma acostumbrada de escribir la denominada “ecuación compensadora” en (2.39). Sin embargo, debe hacerse notar que término a término no se da la igualdad que se da entre estas expresiones, pues la población de todas las regiones que al inicio del periodo contaba con edad ω – 1 ha sido excluida de (2.38). Ello se debe a que se ha supuesto que habrán desaparecido con certeza al final del periodo y por ello no contribuyen al total poblacional para el inicio del siguiente. Su presencia al principio del periodo y su posterior desaparición a lo largo del mismo se compensan, por lo que no es necesario añadirlos; es decir, su efecto sólo es apreciado en la mortalidad y, para esa edad, ésta se expresa en las secciones de la matriz de transiciones que han sido excluidas.
![]() (2.39)
(2.39)
donde Bi(t+1) representa al número de nacimientos ocurridos a lo largo del periodo; Di(t+1) , al de fallecimientos; Si(t+1) finalmente, al saldo migratorio correspondiente.
A partir de (2.38), la “ecuación compensadora” puede ser entonces re-escrita como se muestra en (2.40), para el modelo markoviano.
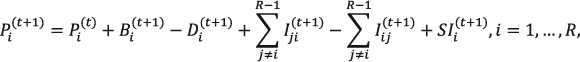 (2.40)
(2.40)
donde ahora Iij(t+1) es el número de migrantes internos desde i a j a lo largo del periodo t + 1; en consecuencia, ![]() es el saldo migratorio interno; y SIi(t+1), el saldo migratorio internacional.
es el saldo migratorio interno; y SIi(t+1), el saldo migratorio internacional.
Varios métodos convencionales, una vez proyectados los comportamientos que se espera tenga cada una de las componentes a partir de las hipótesis correspondientes, calculan las proyecciones del tamaño poblacional mediante (2.39). En particular, las hipótesis sobre la manera en que se modela el comportamiento del saldo migratorio interno son determinantes para lograr una adecuada distribución espacial de la población proyectada. Cuando cada uno de los saldos de las entidades federativas es proyectado de manera independiente (es decir, sin considerar los saldos de las otras), no es difícil imaginar situaciones en las que la distribución espacial sufre distorsiones importantes al paso del tiempo. En contraste, es de esperarse que el modelo presentado, ya que permite que la migración interna sea obtenida a partir de una matriz de orígenes y destinos, permita mejorar los resultados de las proyecciones al compensar exactamente entradas y salidas para cada entidad federativa por migración interna. En particular, se tiene que en el modelo markoviano el saldo nacional para migración interna cumple con
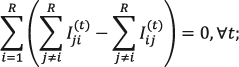
es decir que, como es deseable, la suma de los saldos migratorios internos se anula sin necesidad de recurrir a procedimientos que lograrán que aún saldos disparatados, de esos que distorsionarán de manera importante la estructura por entidad federativa, también sumen a cero.
2.7 Aplicaciones
En esta sección serán discutidas de manera breve algunas de las aplicaciones del modelo descrito en secciones anteriores. Algunas de ellas son evidentes, pero otras representan novedades pues se alejan del camino tradicionalmente seguido por autores que han trabajado con formas más simples de modelos semejantes. Iniciaremos estableciendo las condiciones bajo las cuales el modelo puede ser utilizado para realizar proyecciones de población y las ventajas que su uso puede representar sobre métodos más tradicionales. Inmediatamente después el uso de “proyecciones restringidas” que, además de las tasas tradicionales, incorporan en la estimación a la estadística demográfica reciente y, con ella, a los efectos de influencias exógenas de corto plazo; de este modo, producen estimaciones en las que la experiencia estadística contribuye a dar forma a la evolución de los tamaños de las subpoblaciones involucradas. La experiencia relativa a algunos ejercicios censales fallidos o deficientes, así como la necesidad de contar con series quinquenales o decenales completas, hace pensar en la posibilidad de partir tanto de un censo anterior como de uno posterior para obtener una estimación alternativa de la situación que el censo intentó describir. Bajo el supuesto de que las estadísticas demográficas mejoran su calidad al paso del tiempo, la segunda opción, la de la retroproyección, parece ser más deseable que la primera, por lo que la comentaremos en tercer lugar. Por último, y ya que el modelo abre la posibilidad de realizar estimaciones de corto plazo, se plantea la posibilidad de hacer uso de estimaciones de tasas trimestrales obtenidas a partir de la ENOE para la incorporación de patrones estacionales, principalmente debidos a fenómenos migratorios de corta duración, en la estimación de la evolución poblacional.
Proyecciones
La forma recursiva que asumen las ecuaciones que se utilizan en la actualización de las estructuras por edad, sexo y región sugiere que en tanto se cuente con todas las tasas involucradas para cada uno de los años considerados, la estimación del comportamiento futuro promedio de dichas estructuras podrá ser llevada tan lejos como se desee. Por supuesto, la literatura especializada da cuenta de una variada colección de metodologías cuyo fin es el de elaborar proyecciones de los tamaños y estructuras poblacionales de una región, de un país y de sus divisiones administrativas. Sin embargo, es nuestro parecer que el modelo planteado en el presente trabajo puede competir favorablemente tanto si se presentan las condiciones ideales como si no.
En presencia de condiciones ideales, identificamos al menos dos circunstancias favorables. En primer lugar se tiene la consideración simultánea de las influencias demográficas, así como la de sus interacciones, caso que queda mejor ilustrado cuando algunos valores de las tasas sufren modificaciones, lo que trae consecuencias sobre la evolución de las otras componentes demográficas; por ejemplo, es claro que una reducción en la emigración tiene como inmediata consecuencia aumentos tanto en el número de muertes ocurridas en la región como en el de nacimientos, pues la población expuesta al riesgo será mayor que la contemplada por la proyección. La segunda circunstancia favorable a la que nos referiremos tiene que ver con el hecho de que las proyecciones, sea cual sea el método que se utilice para su elaboración, tienen que ver sólo con un comportamiento promedio, tal vez apelando a alguna ley de grandes números. Sin embargo, la consideración de diversas subpoblaciones trae aparejada la consideración de números cada vez menores y, en consecuencia, una mayor incertidumbre alrededor de tales comportamientos promedio. El enfoque markoviano se presta de manera especialmente natural a la evaluación de las mencionadas precisiones por la vía de ejercicios de simulación. En general, cuando no se considera la fecundidad, la suma de las probabilidades de transición presentes en cada renglón debe ser igual a 1, con lo que se determina una distribución multinomial sobre la población que se encuentra en el estado correspondiente al inicio de cada periodo.
A través de repetidas proyecciones simuladas será posible determinar un rango de valores entre los que, con alta probabilidad, se encontrará el tamaño futuro de las subpoblaciones. Es de esperarse que la acumulación de las desviaciones con respecto al promedio al paso del tiempo dé lugar a precisiones cada vez peores, mismas que, en algunos casos, pueden conducir a proyecciones cuya utilidad será, en el mejor de los casos, dudosa. Sin embargo, algunas mediciones relacionadas, como los montos necesarios para cubrir las pensiones de los adultos mayores o su atención médica —los que también variarán con cada simulación—, podrán también ser delimitadas con razonable precisión en estudios sobre las consecuencias del envejecimiento poblacional.
Cuando las condiciones no son ideales, esto es, cuando no se dispone de conjuntos completos de tasas de fecundidad, mortalidad o de migración, la ya mencionada consideración de los efectos principales de las componentes demográficas y de sus interacciones ayudarán a paliar las deficiencias en la información disponible.
Conciliación demográfica
Por este término entendemos obtención de estimaciones poblacionales aún para periodos en el pasado reciente para obtener una serie más frecuente de lo que permiten los ejercicios censales y añadiendo a los recursos anteriores la estadística de registros administrativos y/o encuestas demográficas para actualizar las mencionadas estimaciones, lo que puede llevar hasta la corrección de los resultados censales. En términos del modelo presentado, equivale a imponer la restricción de que el resultado de la aplicación del modelo debe ser igual a lo observado, en su caso, lo que a su vez tiene influencia en los resultados subsecuentes a manera de valuación de las consecuencias. Sirve, asimismo, para revisar la coherencia entre hipótesis pasadas sobre comportamientos futuros o estimaciones muestrales de tasas demográficas y los hechos registrados.
Retroproyecciones
Significa realizar la misma actividad que en el punto anterior, pero desplazándose hacia el pasado y partiendo de la acumulación de los registros de defunción para un periodo con duración de un quinquenio o de una década. Una aplicación como ésta sería relevante para revisar, por ejemplo, algún resultado censal sobre el que pueda existir alguna duda, como puede ser el caso del censo mexicano levantado en 1980 bajo condiciones particularmente difíciles o algún otro. Ello permitiría complementar la secuencia de resultados poblacionales para un número importante de países. También, servirá para calibrar supuestos y estimaciones muestrales.
Si todas las submatrices involucradas lo permitieran, las retroproyecciones se obtendrían usando la matriz inversa que se muestra en (2.41).
![]() (2.41)
(2.41)
Sin embargo, algunas de estas submatrices resultan ser singulares por lo que sería necesario imponer un número suficientemente grande de restricciones para encontrar una solución única. La parte del vector solución correspondiente a las defunciones aporta una gran cantidad de tales restricciones que son suficientes para encontrar soluciones únicas para cada periodo contemplado en el ejercicio de retroproyección.
Estacionalidad
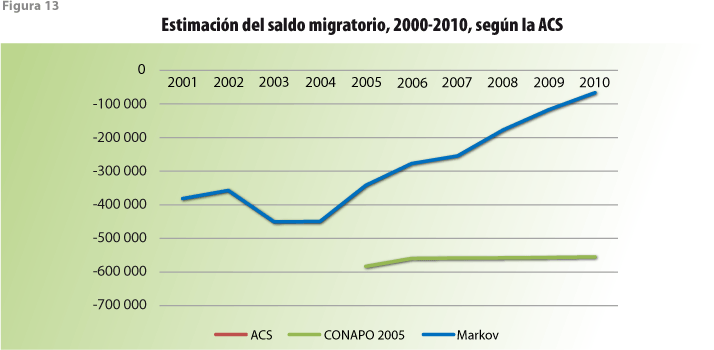
A lo largo de la exposición se ha considerado que el periodo básico de proyección tiene una duración de un año. No obstante, es concebible que periodos con una duración diferente resulten relevantes. Por ejemplo, la ENOE produce estimaciones trimestrales de tasas de desocupación abierta, nacionales y por entidad federativa, entre otras. Sin embargo, tales tasas no toman en cuenta la posibilidad de migraciones estacionales y, en consecuencia, el efecto de éstas sobre las mencionadas estimaciones. La figura 3 exhibe que, bajo ciertas circunstancias, los flujos migratorios internaciones desde y hacia México presentan un comportamiento estacional; es de esperarse que los flujos internos muestren comportamientos similares.
En otras palabras, cabe preguntar si a través del modelo es posible producir estimaciones mensuales o trimestrales para los tamaños poblacionales. La respuesta, por supuesto, es que sí es posible siempre que las edades puedan ser medidas en meses o trimestres y que las tasas trimestrales estén disponibles. Para el caso trimestral, la estacionalidad de la migración podría ser incorporada como sigue:
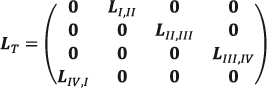
donde ahora se requeriría de un vector de estructuras que además de edad, sexo y región considere al trimestre, y donde Lij modela las modificaciones en las estructuras espaciales al paso del trimestre i al siguiente. Con la puesta en operación de un modelo como el anterior, sería posible evaluar el efecto de las oscilaciones estacionales sobre las estimaciones trimestrales producidas por INEGI, así como sobre las asignaciones presupuestales de recursos fiscales a las entidades. La disponibilidad de tasas trimestrales por edad, sexo y entidad federativa no está lejana. Se trabaja en la explotación simultánea de resultados censales y de los producidos por la hoja de datos sociodemográficos que la ENOE incluye desde hace ya algunos años.
2.8 Resumen
Se ha presentado la construcción de un modelo útil para elaborar proyecciones de población de corto, mediano y largo plazos. Para su exacta aplicación, además del tamaño inicial de la población por cada edad, sexo y estado, se requiere, para cada uno de los años del periodo de proyección y para cada sexo, edad y estado, información acerca de tasas anuales de fertilidad, mortalidad y emigración por estado o país de destino que reflejen las hipótesis sobre el comportamiento futuro de cada componente.
Se ha presentado, asimismo, la forma en que el modelo puede ser usado para calcular recursivamente los tamaños de la población tanto a nivel nacional como para cada una de las entidades federativas.
3. Prueba de estrés del modelo
Según se mencionó, el modelo puede ser utilizado para la elaboración de proyecciones de población cuando los valores de las tasas por edad, sexo y región que resultan de las hipótesis sobre el comportamiento futuro de las componentes demográficas principales son usados en la definición de las matrices de transición para cada periodo y cuando se parte de una estructura poblacional censal corregida por posibles subenumeraciones. Por supuesto, bajo estas condiciones es de esperarse que los resultados obtenidos sean semejantes a los que resultarían de la aplicación de otros procedimientos que hacen un uso eficiente de la información disponible. Es concebible, en consecuencia, que cualesquiera discrepancias que resulten entre los valores proyectados y los observados se deberán al cumplimiento o no de las mencionadas hipótesis demográficas.
Por otro lado, cuando no se dispone de toda la información requerida se presentarán discrepancias mayores entre procedimientos aún en caso de que las hipótesis sigan siendo válidas. Es nuestra opinión que bajo estas condiciones se harán más evidentes las ventajas de disponer de un modelo que, además de los efectos demográficos principales, incorpora las interacciones entre éstos. Sostenemos que el uso de la experiencia estadística y registral a medida que se hace disponible, mediante la imposición de restricciones al comportamiento modelado, subsanarán parcialmente las deficiencias exhibidas por la información disponible al inicio del ejercicio. Para los periodos futuros para los cuales esa información no esté disponible será necesario recurrir a hipótesis sobre la evolución futura de las componentes demográficas, posiblemente aquellas en que se basaron las proyecciones más recientes de población o ajustes de éstas a la luz de evidencia estadística reciente. En otras palabras, el modelo permite la producción de estimaciones híbridas resultado de incorporar de manera paulatina el producto de ejercicios limitados de conciliación demográfica, por un lado, y los de ejercicios tradicionales de proyección, por el otro.
El anterior es el contexto bajo el cual ejemplificaremos la aplicación del modelo descrito en secciones anteriores en la estimación de las estructuras por edad, sexo y región para el 2010 en el 2009, partiendo de una selección de la información recolectada por el censo del 2000. La información censal referida fue complementada con la paulatina incorporación de las estadísticas vitales para los años subsecuentes, así como por información proveniente de encuestas por muestreo periódicas en hogares.
Esta información, junto con sus alcances y limitaciones, será descrita en los párrafos subsecuentes. Enfatizamos que para todos los hechos demográficos y todos los años del periodo de estimación sólo se recurrió a los totales poblacionales provenientes de las fuentes utilizadas, a pesar de que en muchos de estos casos se produce una mucho mayor riqueza de resultados precisos a los que se pudo haber recurrido. Los hechos, las fuentes y los valores poblacionales anuales utilizados se muestran en el cuadro 3.
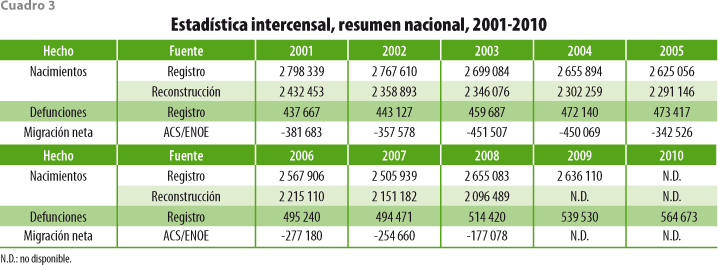
Por lo que toca a la información censal del 2000, se utilizó la de los tamaños de la población censal por grupo quinquenal de edad, por sexo y por entidad federativa. Se incluyó la estimación realizada por el INEGI para las denominadas viviendas sin información de ocupantes, población que fue distribuida proporcionalmente entre los grupos de edad. De esta manera, el tamaño de la población total ascendió a casi 97.48 millones, pero la pirámide de edades, expresada en términos relativos, coincidió con la publicada. De manera alternativa, pudo haberse partido de la población que resultó del ejercicio de conciliación demográfica, asociado a ese censo.
La decisión de hacer uso de información para grupos quinquenales de edad para todo el ejercicio en lugar de la correspondiente a las edades individuales se tomó debido a la forma en que se publicó la del tema migración. El tabulado del que se partió, denominado Población de 5 años y más por estado de residencia actual, sexo y grupos quinquenales de edad, y su distribución según condición migratoria municipal, estatal e internacional (migración por lugar de residencia en enero de 1995), identificado como MIGRACIÓN 4,10 muestra la información precisamente en términos de esos grupos. De hecho, toda la información sobre este tema puede ser obtenida en el mismo sitio del INEGI por edad desplegada a partir de las utilerías de consulta dinámica que esa institución ha hecho disponibles. A pesar de lo anterior, se mantuvo la decisión de trabajar sólo con grupos quinquenales. Por supuesto, queda claro que dicha decisión tiene un efecto adverso en términos de la precisión de las estimaciones, pero por ello nos permite evaluar la bondad del modelo presentado.
La modelación de la migración interna se basó, además, en información sobre cambios de residencia (transiciones) entre una entidad y otra durante el periodo 1995-2000, contenida en el tabulado denominado Población de 5 años y más por entidad federativa de residencia actual y lugar de residencia en enero de 1995, y su distribución según sexo (migración por lugar de residencia en enero de 1995), identificado como MIGRACIÓN 3. En ausencia de información precisa sobre cambios significativos de las tasas derivadas de estos tabulados entre el 2000 y 2010, la estructura se mantuvo fija durante el ejercicio de estimación. La situación es un tanto diferente para la migración internacional ya que al ser determinada a nivel de país puede ser estimada con mayor precisión. De este modo, la situación observada en el 2000 pudo ser modificada a partir de estimaciones aportadas por la American Community Survey (ACS), para 2000-2006, y de las tasas anuales producidas por la ENOE, para 2006-2008. La drástica reducción del saldo migratorio, que tuvo entre sus causas más importantes la contracción sufrida por la economía de los EE.UU. a partir del 2008 (del 2005 para el sector de la construcción, importante empleador de mano de obra mexicana), pudo de este modo ser incorporada en las estimaciones poblacionales para el periodo, contraste importante con el ejercicio de proyección poblacional realizado por el CONAPO y publicado en el 2006, antes de que se hicieran evidentes consecuencias más drásticas de la crisis. La entidad federativa de origen de los emigrantes internacionales, al igual que su edad y sexo, fue asignada proporcionalmente de acuerdo con la emigración interna.
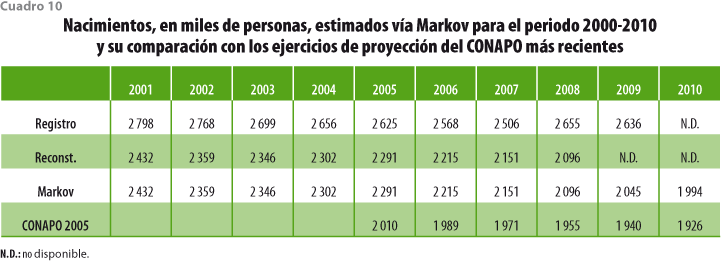
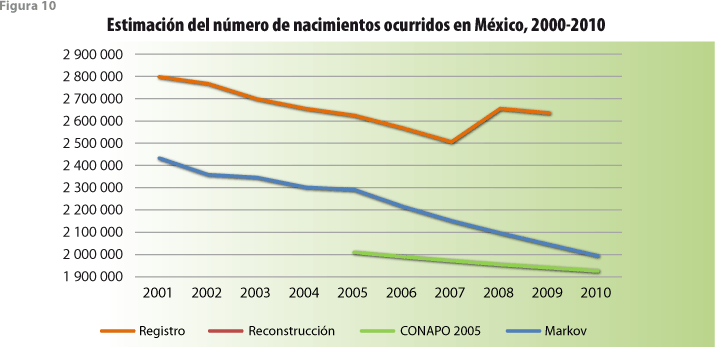
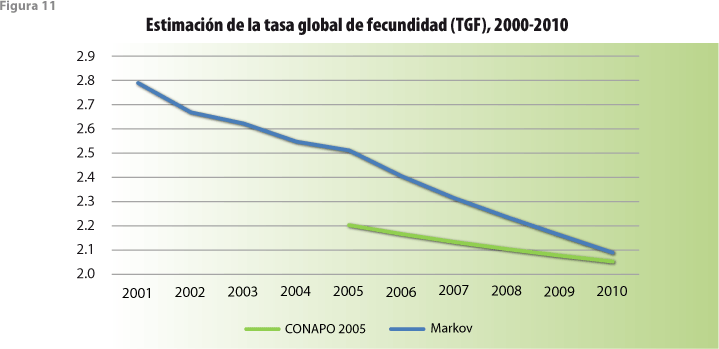
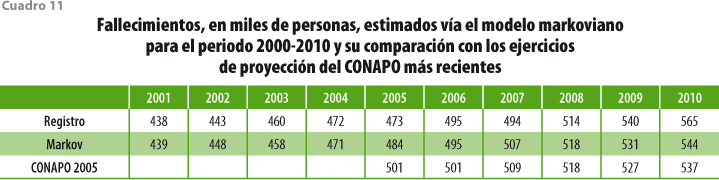
Con respecto a la fecundidad, para el cálculo de tasas por entidad federativa y grupo quinquenal de edad de la madre para 1999, se partió del tabulado denominado Población femenina de 12 a 55 años, último hijo nacido vivo entre enero de 1999 y febrero de 2000 por entidad federativa y grupos de edad de la mujer, y su distribución según fecha de nacimiento del hijo (FECUNDIDAD 4). En ausencia de información adicional, las relaciones que guardan entre sí las mencionadas tasas para diferentes grupos etarios fueron mantenidas constantes a lo largo del decenio 2000-2010. En todo caso, se recurrió, además, a la reconstrucción del número total de nacimientos por año en México, que resulta del análisis de la estadística de registros de nacimiento, pero que requiere del conocimiento de dicho registro para varios años posteriores, por lo que las cifras resultado de la mencionada reconstrucción sólo llegaron al 2008; las cifras para el 2009 y 2010 tuvieron que ser estimadas, lo cual se realizó extrapolando la tendencia que mostraba la reconstrucción. Estos totales nacionales se combinaron con las tasas para 1999 y con los tamaños estimados de los grupos quinquenales de edad femeninos al inicio de cada año del periodo de estimación dando lugar a tasas para cada uno de esos años. Nuevamente, la información proveniente de registros administrativos muestra un despliegue mucho más amplio que el utilizado por nosotros, por lo que podría haber contribuido a mejorar nuestra estimación. Sin embargo, se decidió no hacer uso de dichos desgloses durante esta prueba de estrés del modelo.
Por lo que toca a la mortalidad, también se hizo uso de dos fuentes de información. La primera consistió en un conjunto de tablas de mortalidad calculadas por el INEGI con base en cifras de las proyecciones del CONAPO 2005-2050 usando el paquete MORTPACK. La tabla disponible para cada uno de los años del periodo de estimación no hacía distinción ni por sexo ni por entidad federativa lo que, por supuesto, afecta negativamente la precisión de las estimaciones. Como en los casos anteriores, la segunda fuente informativa usada para dar seguimiento a la mortalidad consistió en la estadística registral publicada por el INEGI. Cabe destacar que sólo fueron usados los totales nacionales por año; es decir, no se aprovecharon los desgloses por sexo, por edad ni por entidad federativa. De nuevo encontramos aquí una fuente de error que pudo haber sido controlado y reducido al aprovechar de manera más eficiente la información disponible.
Bajo las anteriores circunstancias, el ejercicio numérico que se presenta a continuación no es ni un planteamiento de hipótesis alternativas sobre la evolución futura de las componentes de la dinámica demográfica, ni una revisión a fondo de coincidencias o diferencias con resultados censales o de proyección, ni una propuesta de valores poblacionales a ser usados en la práctica. ¿Por qué? Porque las deficiencias en los insumos informativos harían inútil cualquier ejercicio en alguno de estos sentidos.
Lo que se pretende es acercarse al límite de viabilidad del modelo o de las estrategias en las que es posible su aplicación, a distintos niveles de detalle o desagregación.
3.1 Resultados numéricos
Totales nacionales
El cuadro 4 muestra los resultados de la aplicación del modelo restringido a que las estimaciones para cada uno de los hechos coincidan con alguna versión de la estadística demográfica para la década. En el apéndice se hacen explícitos los resultados para cada una de las componentes, así como las discrepancias, en su caso, según el método usado para aproximar la estadística demográfica.
Destacamos que para febrero del 2010, la estrategia seguida resultó en una estimación poblacional de casi 111.95 millones de pobladores en México; cuatro meses después, en junio del mismo año, el censo contó 112.36 millones de habitantes. Es, asimismo, destacable que para febrero del 2005, la estimación alcanzó los 104.9 millones de personas; ocho meses después, durante octubre del mismo año, el conteo de población encontró sólo 103.3 millones.
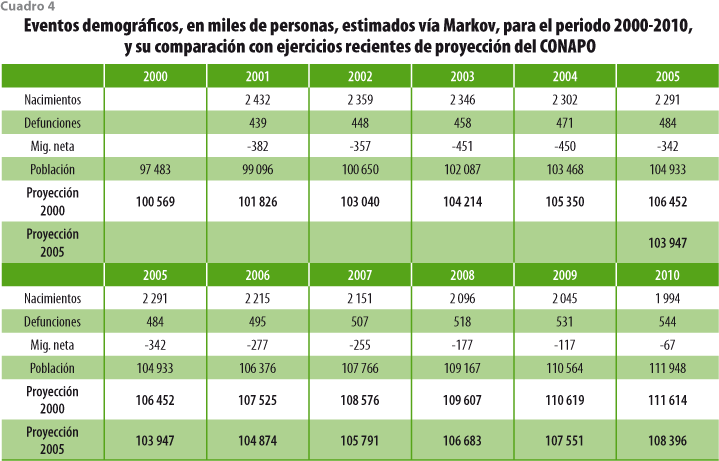
Tal vez los resultados agregados presentados en el cuadro 4 hagan pensar al lector casual que lo mismo pudo haber sido obtenido usando los mismos datos en la aplicación de la ecuación compensadora a lo largo de la década. Por ello, es preciso reiterar que fue necesario hacer ajustes a una o más de las cifras iniciales para que las restricciones impuestas fueran cabalmente satisfechas. De este modo, fue preciso ajustar a la baja las probabilidades de defunción para cada uno de los años. En efecto, sólo cuando se hizo uso de un factor equivalente a 95.26% las tasas de mortalidad fueron adecuadas para obtener, cuando se aplican a la población censal y a las subsecuentes estimaciones, cifras de mortalidad tan cercanas a los valores de las estadísticas vitales como para que las discrepancias entre éstos y la tendencia resultante de la estimación sumaran a cero para toda la década, según se muestra en el apéndice. Si se hubiera iniciado el proceso de estimación haciendo uso de la población conciliada en el 2000, cuyo total alcanzó un valor de 100.6 millones, superior en casi 3.2 millones al de la población censada, habría sido necesario reducir aún más las tasas de mortalidad para reproducir la estadística demográfica de la década. Por supuesto, bajo estas condiciones, la cifra poblacional conciliada por el modelo para el 2010 habría alcanzado los 115 millones de personas. Circunstancias como las descritas en este párrafo en las que, o bien las tasas de mortalidad, o bien la población inicial, o ambas, habrían sido sobreestimadas, sugieren la utilidad del modelo como apoyo a los ejercicios de análisis o conciliación demográfica al señalar posibles inconsistencias entre las distintas fuentes de información consideradas.
Ajustes como los señalados en el párrafo anterior fueron también necesarios para el caso de las otras dos componentes demográficas. Algunos de ellos son consecuencia directa de la aplicación del modelo y de la consideración simultánea de las tres componentes. Por ejemplo, cualesquiera que hayan sido las causas, hay acuerdo en que el número de mexicanos que buscaron emigrar durante la segunda mitad de la década exhibió una importante tendencia decreciente. En consecuencia, creció el número de personas expuestas al riesgo de tener un hijo en este país a lo largo del mismo periodo con respecto a lo que habría cabido esperar. No es de extrañar que las cifras disponibles para la reconstrucción de las estadísticas vitales muestren un decremento más lento en el número de nacimientos que, por ejemplo, lo esperado por el CONAPO al elaborar las proyecciones a partir del 2005. En este contexto cabe, por supuesto, preguntarse sobre el crecimiento o no de la tasa global de fecundidad (TGF) a lo largo de la década. En nuestra experiencia (ver apéndice), con el propósito de reproducir a través de la estimación recursiva el comportamiento de la estadística vital de nacimientos, fue siempre necesario ajustar a la baja las tasas de natalidad de 1999 de modo que la TGF pasó de casi 2.8, para el año que concluyó en febrero del 2001, a 2.1 para el 2010. Por supuesto, en este caso no existe ninguna contradicción.
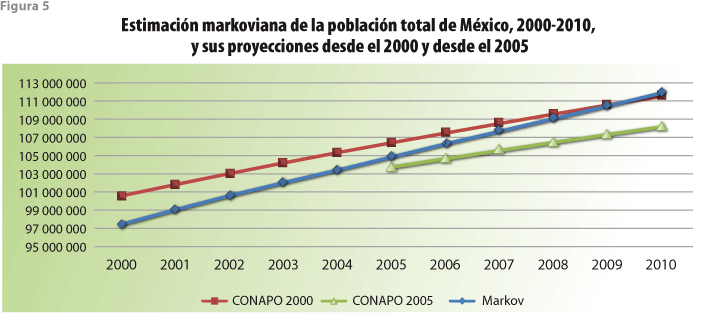
3.2 Estructura quinquenal por edad y sexo
Es posible producir información con un mayor detalle, ya que el modelo fue desarrollado para estimar estructuras por edad, sexo y región o entidad federativa, para todos y cada uno de los años del periodo de estimación. De hecho, la instrumentación que de él se hizo en Excel aporta todos estos resultados que pueden ser solicitados al autor. De cualquier manera, el detalle que para el nivel nacional aporta la distribución por edad y sexo permite crearse una idea del efecto de haber considerado tasas y estadísticas que ignoraron estas características en alguna medida. La figura 6 incluye las estructuras nacionales por edad y sexo para el 2010 tanto en su versión censal como en la estimada por el modelo.
Es preciso destacar que con fines de comparación deben ser tomados en cuenta dos diferencias básicas entre una y otra estructura. En primer lugar, la que resulta del modelo hace referencia a un momento que antecede al censal por cuatro meses, por lo que el crecimiento ocurrido a lo largo de dicho periodo, debido principalmente al crecimiento natural, modificaría ligeramente la estructura presentada. Por su parte, la estructura censal no incluye 1.4 millones de personas imputadas y, por ende, con edades no especificadas (ver cuadro 5).
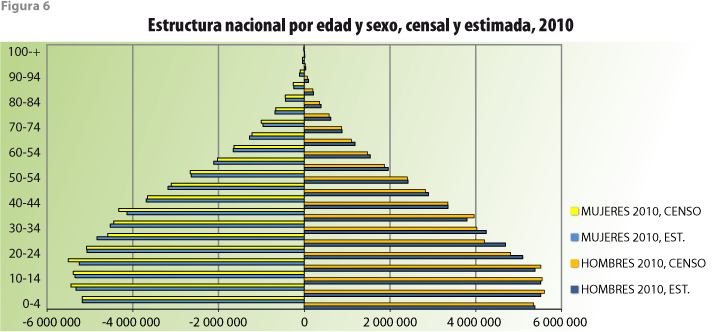
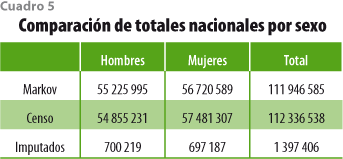
Entre las edades de 20 y 34, para los hombres se nota una discrepancia importante que, seguramente, se verá reducida de manera importante al asignar edades a los no especificados ya que, como se hizo aparente durante la conciliación censal del 2005, cuando se supone que la estructura por edad y sexo para las viviendas sin información de ocupantes es semejante a la exhibida por aquellas que fue necesario visitar dos o más veces durante el levantamiento censal para lograr la entrevista y la cual se carga principalmente del lado masculino y en edades de trabajar. El resto de las discrepancias entre ambas gráficas no parece ser particularmente grande.
3.3 Estructura relativa por entidad federativa
Como ya fue señalado, uno de los usos más importantes de la evolución de los tamaños poblacionales por entidad federativa lo encontramos en la distribución de recursos fiscales de acuerdo con “la última información oficial de población que hubiere dado a conocer el INEGI para la entidad”. Esta información ha estado fuertemente influenciada por las proyecciones de población elaboradas por el CONAPO, pues los factores de expansión son corregidos de modo que su suma coincida con las cifras poblacionales proyectadas a diversos niveles de desagregación. Por ello, y a pesar de la limitación en la información de entrada para la realización de este ejercicio, resulta relevante llevar a cabo una comparación entre ejercicios recientes de proyección y las estimaciones obtenidas por el modelo bajo la estrategia discutida en esta sección. El cuadro 6 muestra la forma en la que, de acuerdo con el modelo, evolucionaron los tamaños relativos de la población para cada una de las entidades federativas durante la pasada década. Con fines de comparación, se presentan también los datos correspondientes a los censos de los años 2000 y 2010, así como los del conteo de población del 2005. Destacamos, de entrada, que las tendencias, tanto crecientes como decrecientes, recogidas por los tres mencionados eventos censales son reproducidas por los resultados arrojados por el modelo. Más aún, que salvo por el Distrito Federal en el 2005 y Jalisco en el 2010, los tamaños relativos reproducidos por el modelo no discrepan por más de una décima de punto porcentual con los obtenidos en los ejercicios censales.
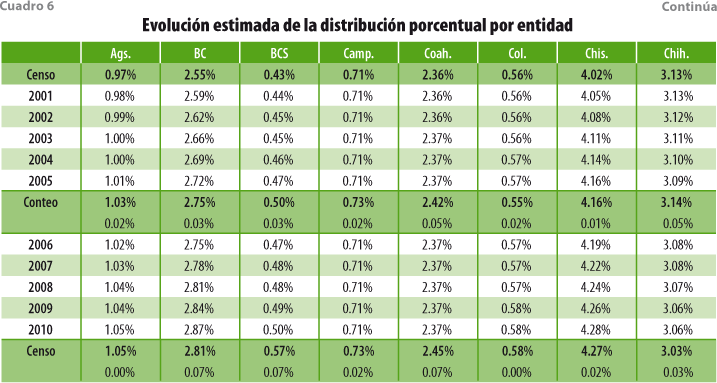
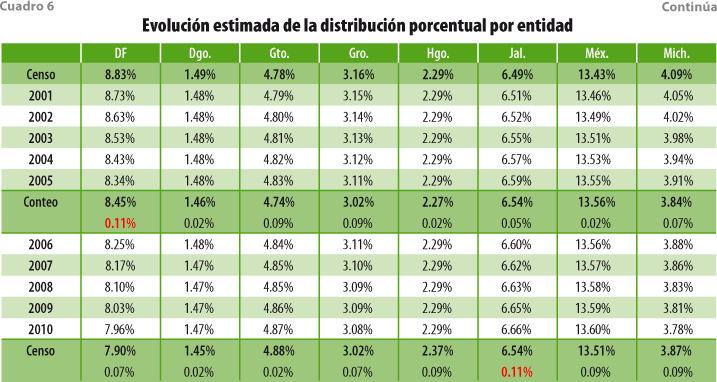
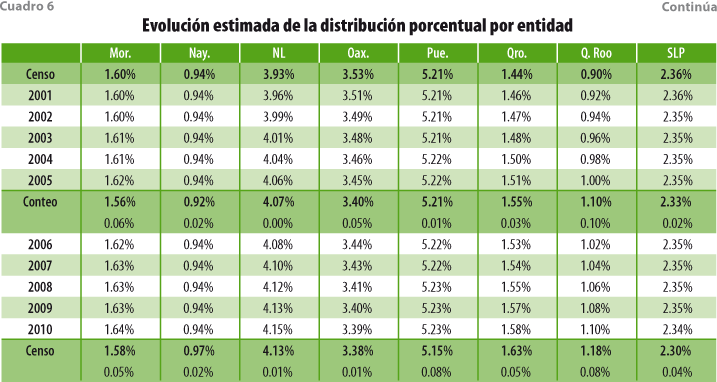
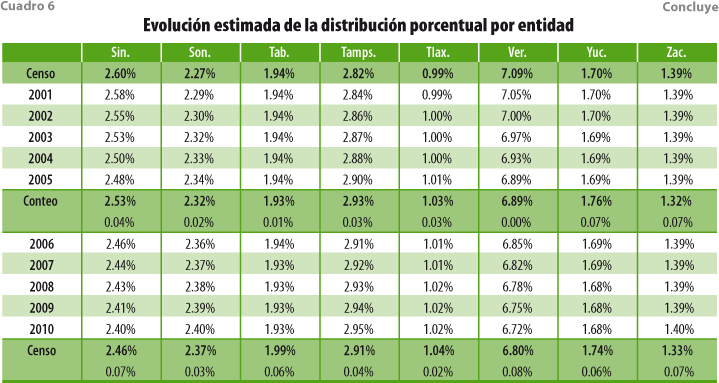
En vista de que la distribución de recursos fiscales se llevó a cabo con base en las proyecciones, y aun cuando la comparación no es pareja, los cuadros 7, 8 y 9 muestran las discrepancias entre las estructuras identificadas por los ejercicios censales y las que resultan de los de proyección poblacional basados en el censo del 2000 y en el conteo del 2005, para los años 2005 y 2010. En el cuadro 7 es posible identificar que ya para el 2005 eran perceptibles discrepancias superiores a la décima de punto porcentual en cinco de las 32 entidades federativas, destacando los recursos en exceso otorgados al estado de México gracias a una discrepancia superior a dos décimas de punto porcentual.
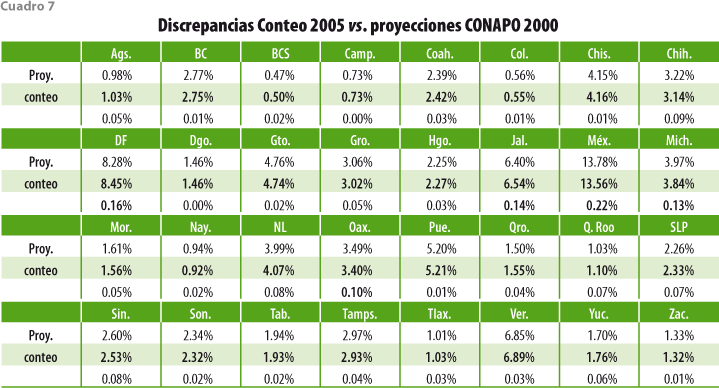
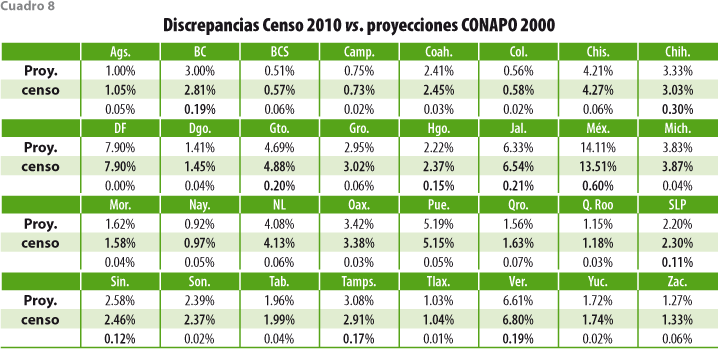
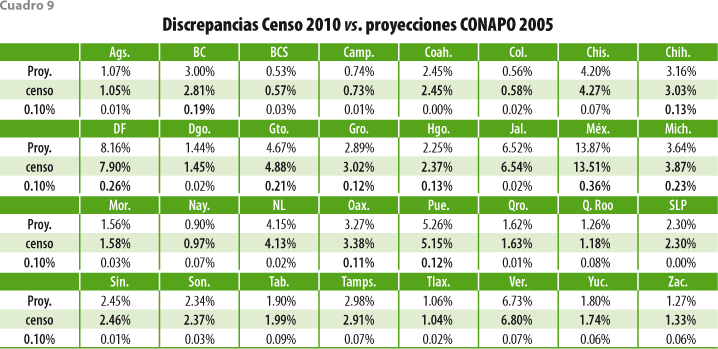
La figura 7 presenta de manera gráfica la comparación de las discrepancias entre los datos censales y tanto los resultados de nuestro modelo como los de las proyecciones elaboradas con base en el censo del 2000 para el 2005. La suma de cuadrados de las discrepancias asociadas a estas últimas alcanza 2.29 veces la primera.
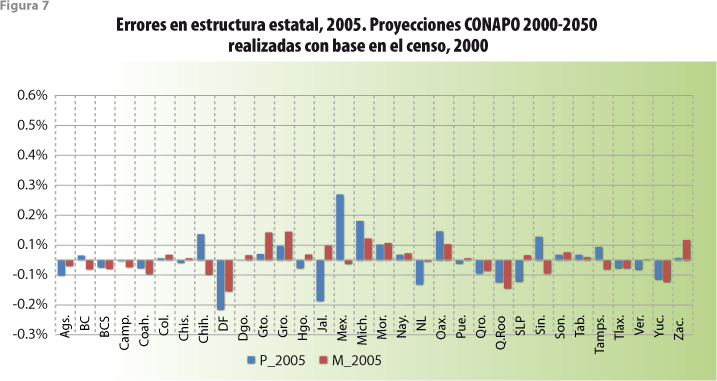
Como sería de esperarse, el cuadro 8 permite realizar la comparación entre las proyecciones elaboradas con base en el censo del 2000 y el levantado en el 2010; muestran ahora discrepancias aún mayores para un número mayor de entidades federativas. En el caso del estado de México, la discrepancia fue superior a medio punto porcentual para ese año. Sin embargo, a Chihuahua se le habrían asignado ingresos en exceso gracias a una discrepancia de casi tres décimas de punto porcentual en tanto que a Guanajuato y a Jalisco, en cambio, se les habrían asignado ingresos inferiores a los que les corresponden gracias a discrepancias entre proyecciones y conteos por casi dos décimas de punto porcentual.
La figura 8 presenta de manera gráfica la comparación de las discrepancias entre los datos censales y tanto los resultados de nuestro modelo como los de las proyecciones elaboradas con base en el censo del 2000 para el 2010. La suma de cuadrados de las discrepancias asociadas a estas últimas alcanza 6.48 veces la primera.
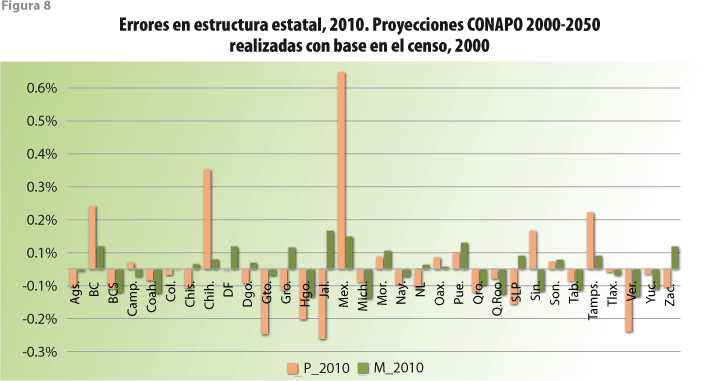
Para el mismo año 2010, pero ahora basados en las proyecciones elaboradas en el 2005, según se muestra en el cuadro 9 y que se refiere al periodo donde se siente el peso mayor de la crisis, encontramos nuevamente discrepancias importantes para las entidades de Baja California, Chihuahua, Guanajuato, Guerrero, Hidalgo, México, Michoacán de Ocampo, Oaxaca, Puebla y el Distrito Federal, superiores a una décima de punto porcentual; de nuevo, la mayor discrepancia se asigna al estado de México.
La figura 9 presenta de manera gráfica la comparación de las discrepancias entre los datos censales y tanto los resultados de nuestro modelo como los de las proyecciones elaboradas con base en el conteo del 2005 para el 2010. La suma de cuadrados de las discrepancias asociadas a estas últimas alcanza 4.04 veces la primera.
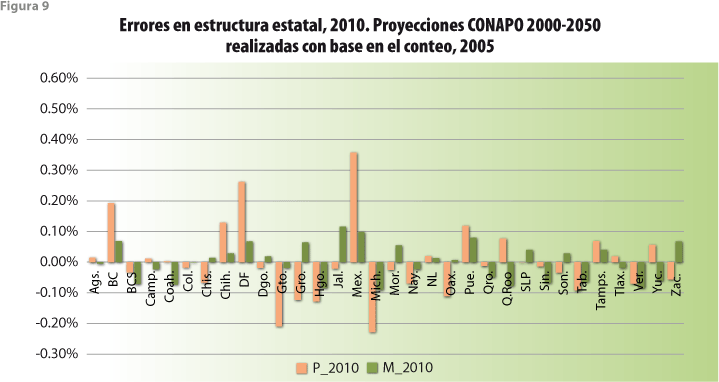
A pesar de las limitaciones informativas tanto al inicio del ejercicio como a lo largo de la década de estimación, la incorporación paulatina de esta tiene evidentes ventajas para fines como los discutidos en este apartado. Cabe esperar que el aprovechamiento eficiente de toda la información que se produce y que se hace disponible al paso del tiempo contribuya a aportar aún mejores resultados.
![]()
Referencias
Bartholomew, D. J. Stochastic models for social processes. New York, Wiley, 1967.
Cox, D. R., H. D. Miller. The Theory of Stochastic Processes. Science Paperbacks. Chapman and Hall/CRC, 1977.
Hoel, P. G., Ch. J. Stone, S. C. Port. Introduction to stochastic processes. Waveland Press, 1972.
Keyfitz, N., H. Caswell. Applied Mathematical Demography. 3ed. Ed. New York, Springer Science+Business Media, Inc., 2005.
Lee, R. D. “Probabilistic Approaches to Population Forecasting”, in: Population and Development Review, 24. Supplement: Frontiers of Population Forecasting, 1998, pp. 156-190.
Leslie, P. H. “On the Use of Matrices in Certain Population Mathematics, Biometrika”, in: Biometrika Trust. Vol. 33, No. 3, Nov., 1945, pp. 183-212.
Partida Bush, V. “Aplicación de cadenas de Markov para proyecciones demográficas en áreas geopolíticas menores”, en: Estudios Demográficos y Urbanos. Vol. 4, Núm. 3 (12), Sept.-Dic. El Colegio de México, 1989, pp. 549-571.
Rogers, A. Matrix analysis of interregional population growth and distribution. XVIII Vienna Congress, Regional Science Association, 1966, pp. 177-196.
![]()
1 “A menudo se confunden ‘fertilidad’ y ‘fecundidad’ como resultado de una mala traducción del inglés. En el ámbito anglosajón su significado es exactamente el opuesto, de modo que ‘fertility’ equivale a ‘fecundidad’ en castellano, y ‘fecundity’ a ‘fertilidad’. Así, el indicador transversal de fecundidad (ISF), se llama en inglés ‘Total Fertility Rate’ (TFR). Como buena parte de la literatura especializada y de las agencias de noticias usan el inglés, la traducción literal y, por lo tanto, errónea, resulta sumamente frecuente.”, consultado en: bit.ly/3LDImPK
4 Por ejemplo, para la estimación trimestral de tasas de desocupación abierta en las entidades federativas ya que algunos numeradores muestran un comportamiento estacional y su estimación ha de considerar este hecho.
5 El apéndice A contiene un breve recuento de los resultados más relevantes a nuestros fines de la teoría de las Cadenas de Markov.
6 En efecto, entre las características más importantes de los procesos markovianos está la propiedad de Markov que, en esencia, dice que la distribución de probabilidad para futuras transiciones condicionada al presente y al pasado depende sólo del estado que actualmente ocupa la partícula y no en la secuencia de transiciones previas que lo llevó hasta ahí. Un proceso con esta característica se denomina un proceso markoviano; para el caso de una Cadena de Markov se dice que si Pr[Xt+r=j|Xt=i0, … , Xt-s=is]= Pr[Xt+r=j|Xt=i0], el proceso {Xt, t ∈ ℜ} es markoviano. La edad alcanzada por una persona es, para nuestros fines, el resumen completo de la única trayectoria que conduce desde el nacimiento hasta esa edad; es decir, resume perfectamente la historia de supervivencia del individuo a lo largo de todas las edades anteriores. Por ello, para determinar la probabilidad de supervivencia futura hasta una edad posterior desde la actual, no es necesario hacer referencia a edades anteriores. Por lo anterior es posible decir que para la supervivencia se cumple estrictamente la propiedad de Markov. Por su parte, las historias migratorias individuales pueden ser mucho más diversas lo que podría determinar diferentes probabilidades de migrar para individuos con la misma edad. Sin embargo, la estadística sobre el tema rara vez hace alusión a tales historias y, en general, se refiere sólo al número de emigrantes a lo largo de un periodo, tal vez relacionado con los originalmente expuestos al riesgo de hacerlo. Bajo estas condiciones, el supuesto markoviano representa una adecuada hipótesis de trabajo simplificadora.
7 En el apéndice A.
8 En lo que sigue, con el fin de mantener la notación simple, las expresiones mostrarán la versión estacionaria, salvo cuando se indique lo contrario.
9 En esta expresión se considera que las tasas específicas por edad de la madre pueden cambiar a lo largo del tiempo.
10 bit.ly/3WhnC5x, consultado el 31 de enero de 2012.
11 Ver Bartholomew, D. J., 1967; Cox, D. R., H. D. Miller, 1977; Hoel, P. G., et al., 1972; y Keyfitz, N. y H. Caswell, 2005, Cap. 11.
Apéndice A.
Elementos de la teoría de las Cadenas de Markov con conjunto finito de estados11
La evolución de múltiples procesos que ocurren cotidianamente, pero que son observados sólo para un conjunto discreto de instantes, pueden ser modelados mediante los modelos conocidos como Cadenas de Markov. Ejemplos:
• Ganancias en la ruleta del casino de la Feria de San Marcos.
• Cumplir un año más de edad o fallecer antes.
• Cambios en el estatus laboral de los individuos pasando por ocupación, desocupación e inactividad económica.
Como se desprende de los ejemplos anteriores, en la práctica, el número de situaciones en que puede encontrarse el sistema en un momento dado puede ser grande, pero finito. Para el caso de la ruleta, las utilidades o pérdidas medidas en unidades monetarias pueden ser muy grandes, pero finitas, y son observadas después de cada jugada. Un individuo de edad x sólo puede encontrarse en uno de dos estados después de transcurrido un año: sobrevivir a la edad x + 1 o fallecer durante el periodo; aun cuando se consideren todas las edades posibles, el número de estados es finito. En México, sin importar qué tan rápido cambie el estatus laboral de una persona, es observado para una muestra trimestralmente cuando la registra la Encuesta Nacional de Ocupación y Empleo. Dicho conjunto de circunstancias puede ser representado, en general, por E = {1,2, …. , j, … , K < ∞} que es un conjunto discreto cuyos elementos representan los estados que un sistema puede ocupar.
El sistema, representado por la secuencia {Xt, t = 0,1,2,3,…}, se desplaza de un estado a otro al paso de cada unidad de tiempo t y donde t = 0 representa el momento en que iniciamos la observación, ya que el sistema puede haber estado en evolución durante algún tiempo. Interesa modelar las leyes que regulan la transición desde el estado i, en que se encuentra la partícula al instante t, hasta alguno de los estados j en el que se encontrará la partícula en el instante t + 1. Dichas transiciones son tratadas como si fueran aleatorias. Su evolución es modelada a través de las denominadas probabilidades de transición:
![]() (A.1)
(A.1)
Note que para el tercer ejemplo estas probabilidades pueden cambiar rápidamente al transcurrir el tiempo (patrón estacional, recesión económica, etc.); para el segundo pueden cambiar, pero más lentamente. Por último, no cambian para el primero. Cuando las probabilidades de transición no dependen del transcurrir del tiempo se dice que la cadena es estacionaria; en este caso, serán denotadas simplemente como Pij.
Las probabilidades de transición pueden ser ordenadas en la denominada matriz de transición, que toma la forma (A.2) para una cadena estacionaria. Como se verá más adelante, partes de una tabla de mortalidad pueden ser expresadas en los mismos términos, lo que explica el interés por esta expresión y las subsecuentes.
 (A.2)
(A.2)
donde ![]() ; es decir, aunque finito, el conjunto de estados es exhaustivo de modo que, partiendo del estado i al tiempo t, el sistema se encontrará en uno y sólo uno de los estados contenidos en E al tiempo t + 1.
; es decir, aunque finito, el conjunto de estados es exhaustivo de modo que, partiendo del estado i al tiempo t, el sistema se encontrará en uno y sólo uno de los estados contenidos en E al tiempo t + 1.
A.1 Probabilidades de transición a r periodos para cadenas estacionarias
Denótese por ![]() a la probabilidad de que la partícula se encuentre en el estado j después de r periodos habiendo partido del estado i. Una definición precisa está dada en (A.3). Para el caso de la sobrevivencia, se trataría de las probabilidades de que un individuo de edad x siga vivo r periodos después o de que haya fallecido durante alguno de ellos.
a la probabilidad de que la partícula se encuentre en el estado j después de r periodos habiendo partido del estado i. Una definición precisa está dada en (A.3). Para el caso de la sobrevivencia, se trataría de las probabilidades de que un individuo de edad x siga vivo r periodos después o de que haya fallecido durante alguno de ellos.
![]() (A.3)
(A.3)
En particular, para r = 2 se tiene (A.4), cuya forma coincide con la entrada ij de la matriz que resulta de multiplicar a la matriz ∏ consigo misma según se indica en (A.5).
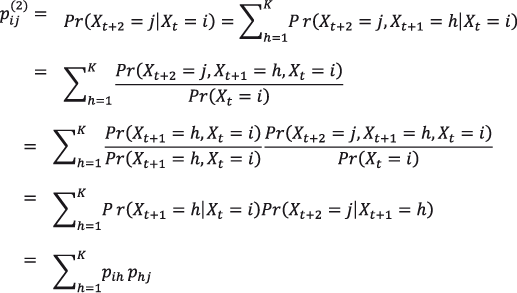 (A.4)
(A.4)
![]() (A.5)
(A.5)
Lo anterior se generaliza de inmediato de modo que es fácil ver que los valores de (A.3) no son otra cosa que las entradas ij de la r-ésima potencia de la matriz ∏, como se indica en (A.6).
![]() (A.6)
(A.6)
La expresión en (A.6) es sólo un caso particular de la denominada ecuación de Chapman-Kolmogorov, que se muestra en (A.7).
![]() (A.7)
(A.7)
A.2 Probabilidades absolutas o probabilidades incondicionales
En este apartado comentaremos de forma breve sobre la determinación de la probabilidad de que el sistema se encuentre en el estado i al tiempo t, independientemente del estado de origen; es decir, la determinación de ![]() . En particular, se tiene que la probabilidad de que al inicio de nuestra observación la partícula se encuentre en el estado i está dada por (A.8). En la aplicación a la demografía que se propone estas probabilidades se harán coincidir con las estructuras por edad, sexo y entidad federativa. En este contexto serán interpretadas como las probabilidades de que al elegir al azar a un residente de algún país o región en algún instante t, su edad sea x; su sexo, y; y su entidad de residencia, z.
. En particular, se tiene que la probabilidad de que al inicio de nuestra observación la partícula se encuentre en el estado i está dada por (A.8). En la aplicación a la demografía que se propone estas probabilidades se harán coincidir con las estructuras por edad, sexo y entidad federativa. En este contexto serán interpretadas como las probabilidades de que al elegir al azar a un residente de algún país o región en algún instante t, su edad sea x; su sexo, y; y su entidad de residencia, z.
![]() (A.8)
(A.8)
Para el cálculo de probabilidades semejantes para 1 periodo posterior, se tiene en principio a (A.9).
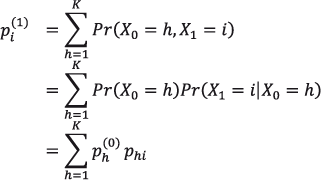 (A.9)
(A.9)
i = 1, … ,K. La expresión en (A.9) coincide ahora con el producto entre un vector renglón y la i-ésima columna de la matriz ∏. El vector renglón es el transpuesto de aquél cuyas entradas están dadas por las probabilidades absolutas definidas en (A.8) y que será representado por ![]() . El conjunto de todos los resultados exhibidos en (A.9) puede ser ordenado en otro vector que será denotado por
. El conjunto de todos los resultados exhibidos en (A.9) puede ser ordenado en otro vector que será denotado por ![]() . El resultado queda dado por (A.10).
. El resultado queda dado por (A.10).
![]() (A.10)
(A.10)
El superíndice t indica que se trata de los vectores transpuestos. Los vectores cuyas componentes son los valores de dichas probabilidades para los periodos futuros están dados por (A.11), para , r = 2 y por (A.12), en general.
![]() (A.11)
(A.11)
![]() (A.12)
(A.12)
Cuando la cadena no es estacionaria, se tiene que las probabilidades de transición cambian al paso del tiempo. Este hecho se representará a partir de una sucesión de matrices de transición {∏(h),h = 0,1,2,}, cada una de las cuales corresponde a un periodo igual o posterior al inicio de nuestra observación. Bajo estas condiciones, (A.12) se convierte en (A.13).
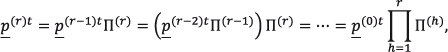 (A.13)
(A.13)
donde la matriz ∏(h) resume las condiciones en que el sistema transitará de unos estados a otros durante el periodo h. En general, es de esperarse que los cambios que puedan darse a lo largo del periodo de proyección serán suaves y siguiendo una clara tendencia, por lo que cuando se consideren periodos cortos se lograrán aproximaciones razonables usando (A.12). Es claro que la necesidad de contar con expresiones como (A.13) se da cuando puedan ocurrir cambios abruptos o puntos de corte que modifiquen la dinámica de manera drástica.
Apéndice B.
Cuadros y gráficas complementarios