Sesgos en la medida de convergencia de los indicadores componentes del Índice de Rezago Social de las entidades federativas de México

 

Biases in the Convergence Measure of the Component Indicators
of the Social Backwardness Index of the Federal Entities of Mexico

 

Óscar Peláez Herreros
El Colegio de la Frontera Norte, sede Tijuana, opelaez@colef.mx

Vol.11 Núm.1 – Epub                                                         Sesgos en la medida… Epub

El artículo comprueba si los estados con mayores niveles de rezago social fueron los que disminuyeron más sus carencias durante el periodo 2000-2015. Se argumenta y explica que la variación absoluta es una medida sesgada hacia la detección de convergencia en la evolución de las variables que forman parte del Índice de Rezago Social. Para evitar este inconveniente, se propone el uso de tasas de variación. Posteriormente, se aplican las técnicas para detectar β-convergencia en datos de sección cruzada y en modelos de datos de panel. Los resultados obtenidos con las tasas difieren sustancialmente de los de las variaciones absolutas, mostrando convergencia solo en algunas variables y periodos temporales. Los casos de divergencia son predominantes. Palabras clave: variación absoluta; variación relativa; divergencia.

This paper verifies whether the states with the highest levels of social backwardness experienced greater reductions in their gaps during the period 2000-2015. We argue and explain that absolute variation is a biased measure towards the detection of convergence in the variables of the Social Backwardness Index. To avoid this trouble, we propose the use of variation rates. We apply techniques to detect β-convergence in cross-section data and in panel data models. The results obtained with the variation rates differ substantially from those of the absolute variations, showing convergence only in some variables and time periods. Divergence cases predominate. Key words: absolute variation; relative variation; divergence.

Recibido: 3 de junio de 2019.
Aceptado: 17 de septiembre de 2019.

 

Introducción

El Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) se presenta en su sitio web como un organismo “…con autonomía y capacidad técnica para generar información objetiva sobre la situación de la política social y la medición de la pobreza en México…” (2019). De hecho, la Ley General de Desarrollo Social (LGDS) le confiere la facultad y responsabilidad de establecer los lineamientos y criterios para la definición, identificación y medición de la pobreza (DOF, 2004). Por ello, calcula las cifras de pobreza multidimensional para los estados y municipios del país, así como las líneas de pobreza por ingresos o el Índice de Rezago Social (IRS).

El CONEVAL publicó los resultados más recientes del IRS, los del 2015, y comparó los valores de las 11 variables que lo componen a nivel de entidades federativas para el 2000, 2005, 2010 y 2015. Estas variables informan sobre carencias relacionadas con la educación, el acceso a los servicios de salud, la calidad de la vivienda, los servicios básicos en la vivienda y los activos del hogar. Asimismo, analizó su evolución en el tiempo, concluyendo que las carencias no solo se redujeron en todos los estados durante el periodo 2000-2015, sino que, además, “…aquellas entidades que han mostrado las mayores disminuciones son también los estados con los mayores niveles de rezago social, que son las regiones en las que la política de desarrollo social ha centrado sus mayores esfuerzos…” (CONEVAL, 2016a: 10).

El objetivo de este artículo consiste en demostrar que la primera parte de esta última cita no es necesariamente cierta; en concreto, que los estados que presentaron mayores niveles de rezago social no son los que tuvieron más reducciones en sus carencias. La hipótesis de trabajo es que la medida que utilizó el CONEVAL para cuantificar la disminución de las variables estaba sesgada hacia la detección de superiores avances en las entidades con mayores valores iniciales. El uso de otras medidas de variación arroja resultados distintos.

Con el propósito de verificar esta cuestión, en primer lugar se explica el razonamiento que siguió el CONEVAL (2016a), el cual muestra que existe un sesgo en la medida que usa para cuantificar la reducción de las carencias; posteriormente, se justifica el empleo de otras medidas de variación que no presentan ese sesgo; en la tercera sección se aplican estas a los datos obteniendo resultados que se comparan con los del CONEVAL (2016a); el último apartado contiene las conclusiones del artículo, que aplican a la interpretación de las dinámicas de las variables del IRS, pero que también se pueden extender a las de los índices de Marginación (IM) y de Desarrollo Humano (IDH), como se desprende, por ejemplo, de la lectura de Aparicio (2004: 28) y PNUD (2003: 61-2).^[1]

Cálculos e interpretaciones del CONEVAL

Esta institución comenzó a calcular el IRS en el 2007 con datos del II Conteo de Población y Vivienda 2005. Se trató de una “…primera aproximación […] para caracterizar el fenómeno de la pobreza en México desde una perspectiva multidimensional y territorial…” (CONEVAL, 2007: 15). La actualización más reciente del IRS es la publicada en el 2016, que acumula información quinquenal para el periodo 2000-2015 a nivel de entidades federativas y municipios.

Al medir los rezagos de manera homogénea en el espacio y tiempo, el IRS facilita la identificación de los municipios y estados del país con mayores carencias, lo cual es útil, por ejemplo, para una mejor toma de decisiones en materia de política social. En concreto, el IRS se calcula como la suma ponderada de los valores estandarizados de las siguientes 11 variables expresadas como porcentajes: 1) población de 15 años o más analfabeta, 2) población de 6 a 14 años que no asiste a la escuela, 3) población de 15 años y más con educación básica incompleta, 4) población sin derechohabiencia a servicios de salud, 5) viviendas con piso de tierra, 6) viviendas que no disponen de excusado o sanitario, 7) viviendas que no disponen de agua entubada de la red pública, 8) viviendas que no disponen de drenaje, 9) viviendas que no disponen de energía eléctrica, 10) viviendas que no disponen de lavadora y 11) viviendas que no disponen de refrigerador (CONEVAL, 2016a: 3). Al calcular el IRS, estas variables se estandarizan para evitar que aquellas con mayores valores numéricos dominen el comportamiento del conjunto. Por su parte, las ponderaciones del Índice se obtienen aplicando análisis de componentes principales. Ello permite que estas sean óptimas en el sentido de que hacen máxima la variación de los datos originales que el Índice logra retener.

Debido a estas características del procedimiento de cálculo, el promedio de los valores del IRS es exactamente igual a 0 y su varianza, a 1 para cada año y nivel de desagregación territorial. Por construcción del Índice, su posición media y dispersión son constantes en el tiempo. Para que una entidad federativa reduzca su IRS, necesariamente otra u otras han de soportar aumentos, pues tienen que mantenerse las condiciones mencionadas:

Como señalan Gutiérrez y Gama (2010: 233), las comparaciones de valores del IRS únicamente son válidas en términos relativos, pero no absolutos: “…no pueden ser comparados de manera directa los cambios observados en el valor de los índices […] de una unidad geográfica particular en dos momentos en el tiempo…”. Esto es así porque sus valores se obtienen en relación con todas las demás unidades geográficas en el mismo momento. La reducción del IRS en una entidad federativa, por ejemplo, es señal de que ha evolucionado mejor que el promedio, pero no indica cuánto ha avanzado en el combate a los rezagos que padece la población que reside en ella. Para conocer esta cuestión, ha de examinarse la dinámica específica de cada una de las variables originales que componen el Índice.

La gráfica que se muestra enseguida representa los valores del IRS para los estados del país. Como se observa, sus recorridos tienden a ser estables a lo largo del tiempo. No se advierten grandes variaciones en los 15 años que abarca el indicador. Distintos factores contribuyen a esa estabilidad. En primer lugar, que las variables que integran el Índice hagan referencia a aspectos estructurales, que dependen fuertemente de sus valores pasados; a ello se suma el hecho de que el IRS sea el resumen de 11 variables, por lo que la evolución de unas puede compensarse con otras; además, se expresa en relación con el conjunto de unidades territoriales, de manera que no es suficiente con que una entidad federativa mejore (o empeore), sino que ha de hacerlo con una diferencia clara respecto al promedio.

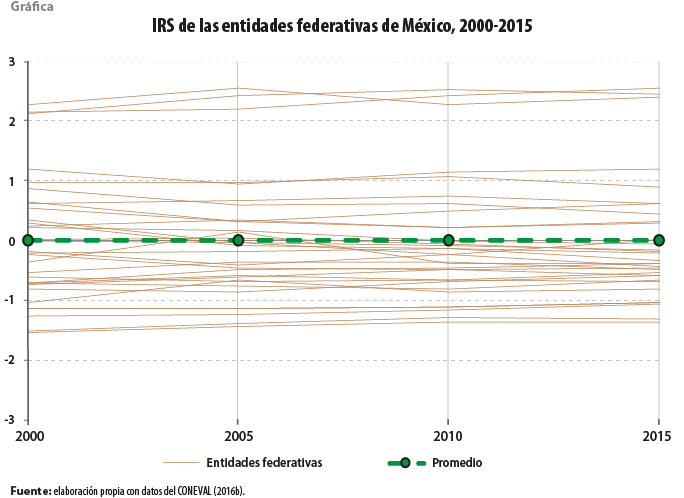
Aparte de la estabilidad en el tiempo, en la gráfica también se destaca la brecha existente entre el grupo de tres estados con IRS más alto y el resto de las entidades federativas: estos son Guerrero, Oaxaca y Chiapas, que de manera sistemática han alcanzado valores por encima de 2 en el Índice, distanciándose en más de un punto de la siguiente entidad federativa, Veracruz de Ignacio de la Llave o Puebla, dependiendo del año. A la vista, no se aprecia ningún acercamiento de los estados con mayor rezago social hacia los mejor posicionados. De hecho, incluso, parece lo contrario. Al comparar las cifras del 2000 con las del 2015, se tiene que el IRS aumentó en esas tres entidades del Pacífico sur de 2.27 a 2.39 en Chiapas, 2.16 a 2.54 en Oaxaca y 2.12 a 2.45 en Guerrero, lo cual implica un alejamiento respecto al promedio nacional.

El CONEVAL (2016a) no presta mayor atención a la evolución del IRS a lo largo del tiempo, se limita a señalar que en el 2015 había cuatro entidades con muy alto grado de rezago social (Chiapas, Guerrero, Oaxaca y Veracruz de Ignacio de la Llave) y otras cuatro en el extremo opuesto, con grado muy bajo (Aguascalientes, Coahuila de Zaragoza, Distrito Federal^[2] y Nuevo León). No obstante, sí describe con algún detalle la dinámica de cada una de las 11 variables componentes del Índice entre el 2000 y 2015; por ejemplo, para los tres indicadores de rezagos en educación, encuentra avances generalizados durante el periodo de análisis, destacando que: “…En el caso de la población de 15 años o más analfabeta, las reducciones más importantes se dan en Chiapas, Guerrero y Oaxaca, los estados con las mayores carencias. La población de 6 a 14 años que no asiste a la escuela presentó las mayores reducciones en Chiapas, Guerrero y Michoacán de Ocampo. Finalmente, para la población de 15 años y más con educación básica incompleta, las reducciones más importantes tuvieron lugar en los estados de Zacatecas, Hidalgo y Tabasco…” (CONEVAL, 2016a: 4).

De manera similar, para la población sin derechohabiencia a servicios de salud: “…Las reducciones más importantes se dieron en Guerrero, Chiapas y Oaxaca. Dichas reducciones representan más de 55 puntos porcentuales en cada caso…” (Ibíd.: 5).

El resto de las variables siguieron patrones semejantes, siendo esta evidencia acumulada la que lleva a concluir “…que aquellas entidades que han mostrado las mayores disminuciones son también los estados con los mayores niveles de rezago social, que son las regiones en las que la política de desarrollo social ha centrado sus mayores esfuerzos…” (Ibíd.: 10).

No hay error en los cálculos. Cuando se utiliza la variación absoluta (VA) como medida del cambio, los estados con superiores avances son los que inicialmente estaban más rezagados, son los que presentaban mayores valores en las distintas carencias. Con datos del CONEVAL es posible verificar las anteriores y las demás afirmaciones similares del documento, teniendo en cuenta que la VA de una variable i, en una entidad federativa j, durante un periodo T, se obtiene como la diferencia de los valores observados al inicio, 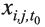, y al final del periodo en cuestión, 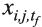, esto es:

Por ejemplo, en relación con el porcentaje de viviendas con piso de tierra, se indica que “…las mayores disminuciones se dan en los estados con mayores carencias: Chiapas, Oaxaca y Guerrero, con disminuciones de más de 20 puntos porcentuales en cada caso…” (2016b: 6). Efectivamente, entre el 2000 y 2015, Chiapas lo redujo de 38.45 a 10.62%, lo que supone una disminución de 27.83 puntos porcentuales; Oaxaca pasó de 39.71 a 13.05%, con una caída de 26.66; y Guerrero lo disminuyó en 23.04 puntos, desde 36.92 hasta 13.88 por ciento.

Si bien los cálculos son correctos y ninguna otra entidad federativa experimentó reducciones tan importantes de sus rezagos, surge una duda que se puede plantear de diversas formas, pero que en esencia es la siguiente: ¿por qué los otros estados no registraron disminuciones tan grandes en las carencias? La respuesta a esta pregunta descubre el inconveniente de usar la variación absoluta como medida de los cambios ocurridos. Con las excepciones de Veracruz de Ignacio de la Llave, Puebla y San Luis Potosí, en el 2000 ningún otro estado soportaba porcentajes de viviendas con piso de tierra superiores a 20%, lo cual implica que era imposible que redujeran este rezago en 20 puntos porcentuales, por ejemplo: en Zacatecas fue 8.95%; en Baja California, 4.95%; en Aguascalientes, 3.52%; y así los demás casos. Zacatecas bajó esta carencia desde el mencionado 8.95% hasta 1.33%, es decir, 7.62 puntos porcentuales.

El problema de la VA como medida de los cambios en las carencias que integran el IRS es que presenta un sesgo que ha de tenerse en cuenta: permite variaciones numéricamente mayores en aquellos estados que parten de niveles iniciales más altos. Lo comentado para las viviendas con piso de tierra aplica del mismo modo al resto de las variables del IRS.

Otras medidas de variación y convergencia

El CONEVAL (2016a) enfatiza la fuerte reducción de las carencias en los estados inicialmente más rezagados. Sin embargo, como se ha expuesto, esa conclusión puede venir inducida por la herramienta utilizada para medir las variaciones a lo largo del tiempo, que está sesgada, precisamente, en el sentido de las conclusiones y resultados obtenidos. Si Guerrero pudo bajar su porcentaje de población sin derechohabiencia a servicios de salud en más de 60 puntos porcentuales durante el periodo 2000-2015 fue, entre otros motivos, porque en el 2000, 78.12% de sus residentes no tenían acceso a este servicio. Para entidades como Sonora o Yucatán, disminuciones de esa magnitud eran en absoluto imposibles, ya que partían de niveles inferiores: 41.75 y 53.88%, respectivamente. Ni siquiera garantizando la derechohabiencia universal a servicios de salud podían conseguirlo.

La comparación de los avances de las distintas entidades federativas en el combate a los rezagos debe realizarse con una medida que, desde el inicio, no limite la capacidad de mejora de los territorios o que, cuando menos, trate a todos por igual. La variación relativa (VR), o tasa de variación (TV), puede ser útil para ello, ya que expresa la disminución en las variables como porcentaje respecto a su valor inicial, permitiendo que cada territorio pueda reducir sus rezagos desde 0 (ningún avance) hasta 100% (completa eliminación de la carencia).^[3] La expresión matemática para el cálculo de la VR es:

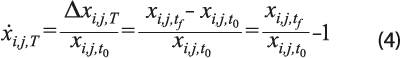
donde 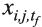es el valor de la i-ésima variable (i = 1, …, 11) para la j-ésima entidad federativa (j = 1, …, 32) al final del periodo de análisis; 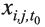_, la observación correspondiente al inicio del periodo T, que abarca desde el momento t₀ hasta t_f² ; y Δx_i,j,T representa la variación absoluta.

La tasa de variación media acumulativa (TVMA) aporta las mismas ventajas que la VR, pero además permite comparar la reducción o aumento de las variables en lapsos de distinta duración, ya que pondera las variaciones con la amplitud del periodo en el que se registran. Su fórmula de cálculo es:

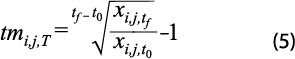
Dado que las variables que se están considerando tienden a reducirse hacia el valor 0, tanto la VR como la TVMA pueden interpretarse en el sentido propuesto por Sen (1981), esto es, como el porcentaje en que se reduce cada carencia en cada territorio: durante el periodo que se esté considerando, en el caso de la VR, o en promedio anual cuando se trata de la tasa de variación media acumulativa.

Estas dos medidas, (4) y (5), ordenan de manera idéntica a las entidades federativas en función de sus mayores o menores avances en el combate de los rezagos sociales. Sin embargo, cabe esperar que haya discrepancias al comparar los estados que más redujeron sus carencias en valores absolutos (3) o en términos relativos (5). Para disponer de una medida de estas discrepancias, se calcula el coeficiente de correlación por rangos de Spearman para cada una de las 11 variables del IRS:

Las entidades federativas se pueden ordenar de mayor a menor variación en una misma variable, durante un mismo periodo, T, tanto en términos absolutos como relativos. Las diferencias de esos dos órdenes se representan mediante d_i,j,T, a la vez que J indica el número de observaciones disponibles, que en este caso son 32 por tratarse de estados. El coeficiente ρ está acotado entre –1 y +1. Valores positivos son señal de concordancia en las ordenaciones generadas por las VA y VR; cuanto más se aproxima ρ a 1, mayor es esta concordancia, hasta llegar al extremo en que ρ = 1 indica que variaciones absolutas y relativas ordenan exactamente igual a las unidades territoriales. En el sentido contrario, los negativos son señal de discordancia. Un valor de ρ = 0 indica que los atributos muestran ordenaciones independientes.

Por otra parte, para evaluar si las entidades más rezagadas experimentaron mayores avances en el abatimiento de las carencias, se propone recurrir a técnicas que consideren la totalidad de datos de la distribución, en vez de solo tres valores extremos. El concepto de β-convergencia puede ser útil en este sentido. Siguiendo a Barro y Sala-i-Martin (1990), en una situación de β-convergencia, la estimación del parámetro β_i,T en la ecuación:

arroja un valor negativo y estadísticamente significativo, indicando que la i-ésima carencia bajó más en aquellas áreas geográficas donde presentaba valores más altos al inicio del periodo T. Al contrario, uno positivo y estadísticamente significativo del parámetro β_i,T es señal de β-divergencia: la carencia en cuestión se redujo más en los estados con menor rezago. Esta expresión es la base de los análisis de convergencia en el producto interno bruto estatal per cápita que, en el caso de México, comenzaron a realizar Juan y Rivera (1996) y Ruiz (1997), y sigue encontrándose en los más recientes del Banco de México (2017: 5-8), Luna y Colín (2017) o Rodríguez y Cabrera (2019), entre otros. Campos et al. (2017) y Peláez (2017) también la han aplicado al análisis del IDH.

A partir de la información disponible para el IRS, la ecuación 7 puede estimarse con cada una de las i = 1, …, 11 variables para el periodo completo, 2000-2015, o para cada uno de los subperiodos quinquenales: 2000-2005, 2005-2010 y 2010-2015.

Además, aprovechando estas tres secciones cruzadas, los datos pueden presentarse en forma de panel, lo que permite estimar modelos de datos agrupados:

y de efectos fijos:

Los modelos de datos de panel ayudan a detectar y controlar los efectos propios de cada unidad territorial que no son captados por la variable explicativa, pero que influyen en las tasas de variación. La ecuación 8 representa el caso de ausencia de especificidades regionales. La estructura de la dinámica de la variable i-ésima es la misma en todos los estados al ser los parámetros α_i y β_i comunes para las unidades territoriales. En este caso, un valor negativo y estadísticamente significativo del parámetro β_i es señal de β-convergencia absoluta en la variable i-ésima durante el periodo 2000-2015. Por el contrario, una estimación positiva y estadísticamente significativa de β_i indica β-divergencia absoluta.

La especificación 9, sin embargo, admite trayectorias diferentes para cada entidad federativa a través de la familia de parámetros α_i,j. En los modelos de efectos fijos, un valor negativo y estadísticamente significativo en la estimación de β_i no es señal de convergencia absoluta, sino de β-convergencia condicionada por las particularidades no observadas, pero contenidas en los α_i,j. Un β_i positivo y estadísticamente significativo muestra que hubo β-divergencia condicionada en la variable i-ésima durante el periodo 2000-2015.

La comparación de los modelos 8 frente al 9 permite conocer si los paneles de datos se describen mejor como procesos de convergencia-divergencia absoluta o condicionada, esto es, si los distintos estados muestran dinámicas comunes o particulares. Para verificar esta cuestión, se realizan contrastes mediante el estadístico:

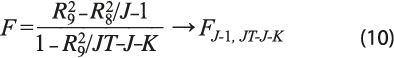
donde representa el coeficiente de determinación del modelo 8; es el coeficiente de determinación del modelo 9; J, el número de unidades territoriales (J = 32, en este caso); T, el número de secciones cruzadas (T = 3); y K, el número de regresores (K = 1). El estadístico F se compara con el valor crítico 1.633, que corresponde a la distribución de probabilidad F con J – 1 = 31 y JT – J – K = 63 grados de libertad y un nivel de confianza de 95 por ciento. Un estadístico F mayor que 1.633 lleva a rechazar la hipótesis de que los modelos 8 y 9 son estadísticamente equivalentes, de manera que cada entidad federativa tiene características específicas que deben tomarse en cuenta mediante los coeficientes α_i,j. En ese caso, el modelo 9, de convergencia-divergencia condicionada, es más adecuado que el de convergencia-divergencia absoluta.

Cuando se prefiere el modelo 9 frente al 8, cabe considerar si es mejor estimarlo con efectos fijos o aleatorios. El contraste de Hausman (1978) aporta información al respecto evaluando la consistencia de los estimadores de mínimos cuadrados generalizados frente a los de efectos fijos. Para ello, se recurre al estadístico:

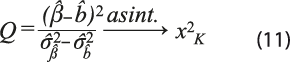
donde es el estimador del modelo de efectos fijos; , el estimador del modelo de efectos aleatorios; y y son sus varianzas respectivas. El estadístico Q se compara con el valor crítico 3.841, obtenido de la distribución de probabilidad χ² con K = 1 grado de libertad y un nivel de confianza de 95 por ciento. Un estadístico Q mayor que 3.841 implica rechazar la hipótesis nula de que los estimadores de mínimos cuadrados generalizados son consistentes, resultando más adecuada la estimación por efectos fijos.

Dos motivos fundamentales permiten anticipar que los modelos de efectos fijos serán preferidos a los de aleatorios. El primero es que se dispone de datos para la totalidad de los elementos que se analizan: las 32 entidades federativas del país. Al no tratarse de una muestra aleatoria, las estimaciones de los parámetros específicos de cada estado tienen sentido en sí mismas. Además, como argumentan Yang et al. (2016: 6), es probable que estos efectos individuales correlacionen con los valores iniciales de las variables, haciendo inapropiada la estimación de efectos aleatorios.

No obstante, también hay que considerar lo expuesto por Martín-Mayoral y Yépez (2013: 211), quienes distinguen entre los tradicionales análisis de convergencia en términos de ingreso o renta y los que se aplican, como es el caso, sobre variables acotadas que necesariamente tienen que converger en el valor mínimo, 0%; por este motivo, lo que realmente cabe esperar es que los modelos de convergencia absoluta (ecuación 8) expliquen mejor lo ocurrido en la realidad que los de convergencia condicionada (ecuación 9).

Resultados

El cálculo de las tasas de variación arroja resultados distintos a los de las VA. En el caso de la población analfabeta, por ejemplo, las entidades que tuvieron mayores avances relativos en el periodo 2000-2015 son Querétaro, Nuevo León y Sonora, que redujeron esta carencia 53.7, 51.0 y 50.3%, respectivamente; en términos absolutos, las tres primeras posiciones correspondieron a Chiapas, Guerrero y Oaxaca (CONEVAL, 2016a: 4). Para la población de 6 a 14 años que no asiste a la escuela, ocurre algo parecido: las mayores reducciones relativas se registraron en Sinaloa (-67.7%), Zacatecas (-67.7%) e Hidalgo (-65.5%), mientras que las variaciones absolutas más importantes fueron las de Chiapas (-9.0), Guerrero (-6.9) y Michoacán de Ocampo (-6.6).

El mismo fenómeno se repite con mayor o menor intensidad en el resto de las variables. Las coincidencias entre los estados con mejor desempeño absoluto y relativo son poco frecuentes. El coeficiente de Spearman permite cuantificar esta cuestión. Como se desprende de los datos del cuadro 1, para algunas variables, como el porcentaje de población sin derechohabiencia a servicios de salud, las VA y las TVMA concuerdan en gran medida (ρ = 0.835) al señalar los estados que más y menos avanzaron en el combate de esas carencias. En otros casos, como las viviendas que no disponen de drenaje (ρ = -0.662) o la población de 15 años o más analfabeta (ρ = -0.449), las ordenaciones de una y otra medida de variación son, incluso, contrarias. También, hay variables para las que, prácticamente, no se aprecia relación entre los estados que evolucionaron mejor en términos absolutos o relativos. Esto último ocurre de manera clara con las viviendas que no disponen de excusado o sanitario (ρ = 0.010) o con las que carecen de energía eléctrica (ρ = 0.004).

Las VA y VR tienden a identificar distintas entidades como aquellas con mejor desempeño en el abatimiento de cada rezago. Ni siquiera en las variables en las que guardan más semejanzas, como la población sin derechohabiencia a servicios de salud, es posible encontrar una concordancia perfecta. Para esta variable en concreto, las mayores reducciones relativas se registraron en San Luis Potosí (-83.3%), Guerrero (-80.8%) y Zacatecas (-80.7%), mientras que las variaciones absolutas más importantes fueron las de Guerrero (-63.1), Chiapas (-60.5) y Oaxaca (-58.8); solo Guerrero repitió entre los tres estados con mejor dinámica. En el extremo opuesto de la clasificación es posible encontrar alguna semejanza más; por sus escasos avances relativos destacaron el Distrito Federal (-54.8%), Baja California (-52.6%) y Coahuila de Zaragoza (-50.5%), mientras que las menores disminuciones absolutas de la carencia en salud se registraron en Baja California (-20.0), Nuevo León (-19.7) y Coahuila de Zaragoza (-14.4). Aun siendo la variable con mayores semejanzas en las VA y VR del periodo 2000-2015 (ρ = 0.835), presenta bastantes discrepancias.

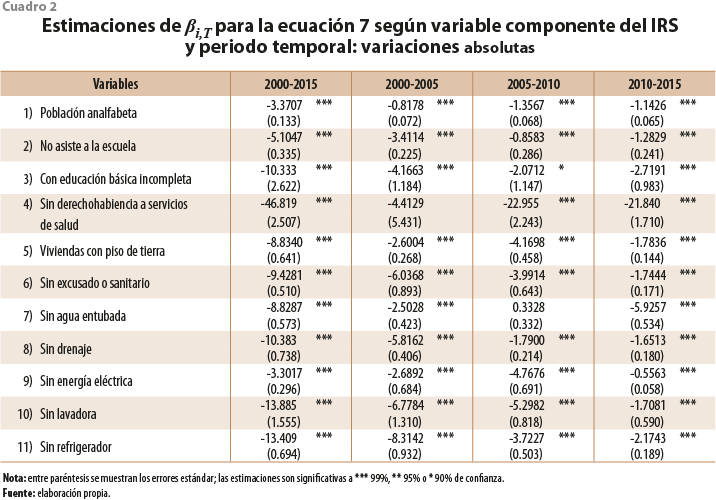
A partir de estas diferencias, en unos casos más importantes que en otros, no cabe esperar otra cosa que conclusiones distintas en relación con la convergencia de las entidades más rezagadas hacia las más avanzadas del país. El cuadro 2 muestra las estimaciones del modelo 7, pero explicando las VA en lugar de las tasas de variación. Como se ha argumentado, las variaciones absolutas están sesgadas en el sentido de poder ser más amplias allí donde los valores iniciales son mayores. Esta relación es, precisamente, la de convergencia: mayor reducción de las carencias en los estados con superiores niveles de rezago social. Las estimaciones del cuadro 2 presentan esa relación. El coeficiente β_i,T es negativo y significativo a 99% de confianza en 41 de los 44 casos estimados. En dos más es negativo, pero significativo a 90% o no significativo, y solo para las viviendas que no disponen de agua entubada de la red pública durante el lustro 2005-2010 muestra signo positivo, aunque la estimación carece de significatividad. Prácticamente, todos los resultados indican la existencia de una intensa relación entre altos niveles de las carencias y mayores reducciones del rezago. De aquí se obtendría la misma conclusión a la que llega el CONEVAL (2016a: 10) analizando los tres valores extremos de cada distribución: “…las entidades que han mostrado las mayores disminuciones son también los estados con los mayores niveles de rezago social…”.

La situación cambia al utilizar una medida de variación que permite a todas las unidades territoriales el mismo progreso, que no limita sus avances desde la definición de la propia medida, esto es, al reemplazar las VA por las TVMA. El cuadro 3 contiene las estimaciones del modelo 7 tal como se especificó en páginas anteriores. En esta ocasión, 33 coeficientes muestran signo positivo y solo 11, negativo reduciéndose, prácticamente, a la mitad los casos estadísticamente significativos. La convergencia deja de ser un fenómeno generalizado para convertirse en un proceso específico de unas pocas variables.

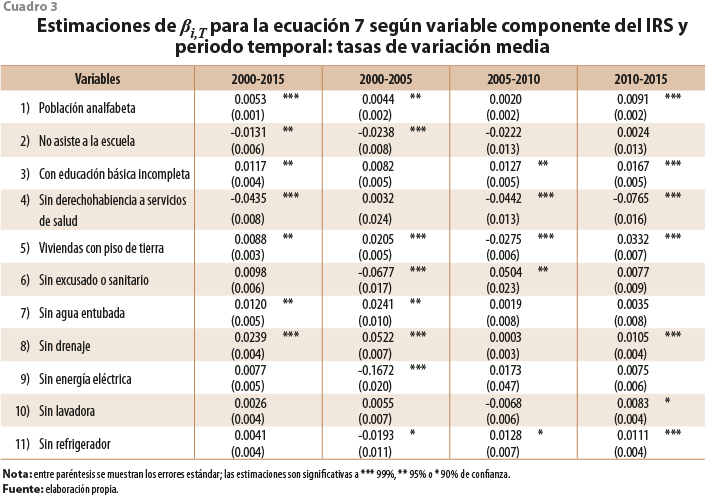
Los signos negativos característicos de la asociación entre mayor nivel de una carencia y mayor reducción de esta en términos de tasas de variación se concentran, sobre todo, en dos variables: la población sin derechohabiencia a servicios de salud, que experimentó procesos de convergencia significativos en los dos quinquenios más recientes y en el periodo 2000-2015 considerado en conjunto, y la población de 6 a 14 años que no asiste a la escuela, con convergencia en el lapso conjunto y en el lustro 2000-2005. Estas son, precisamente, las dos variables con más altos coeficientes de Spearman en el cuadro 1. Al ser los casos con mayores semejanzas entre las VA y las tasas de variación, resulta coherente que las segundas conserven la tendencia a la convergencia que caracteriza a las primeras.

Ninguna de las otras nueve variables del IRS mostró indicios de convergencia entre el 2000 y 2015, solo en algunos subperiodos aislados que se vieron más que compensados por la divergencia que tuvo lugar el resto del tiempo. Así ocurrió con las viviendas con piso de tierra, las que no disponen de excusado o sanitario o aquellas sin energía eléctrica.

Al contrario, la divergencia predominó en el conjunto de casos, siendo significativa en cinco variables para el periodo 2000-2015. Mayores niveles de carencias tendieron a corresponderse con menores reducciones de los rezagos.

Las estimaciones del cuadro 4 para los paneles de datos revelan, de nuevo, una combinación de casos de convergencia y de divergencia. Además, los estadísticos indican que siete de las 11 variables se modelizan mejor mediante la especificación de datos agrupados (ecuación 8), tres con efectos fijos (ecuación 9) y solo una con aleatorios.

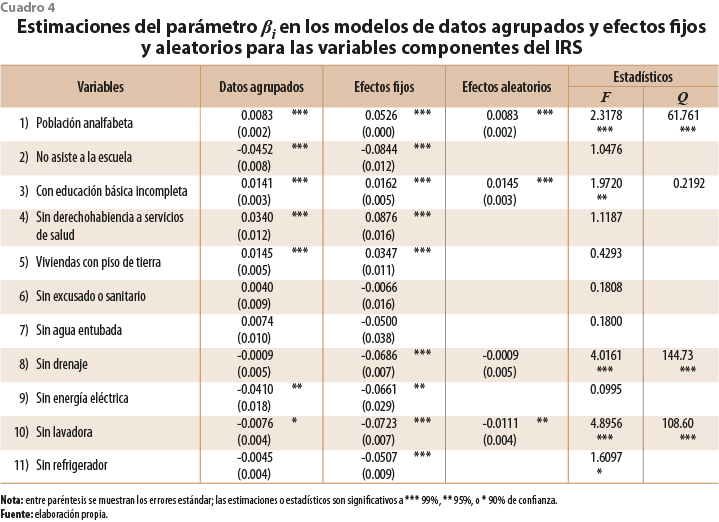
Lo contrario ocurre con el porcentaje de población de 6 a 14 años que no asiste a la escuela. El estadístico F no supera al valor crítico, por lo que el modelo de referencia es el de datos agrupados, en el que la estimación del parámetro β_i es negativa y significativa con una confianza de 99%, indicando que esta variable experimentó convergencia absoluta en el periodo 2000-2015.

La primera variable, el porcentaje de población de 15 años o más analfabeta, es una de las tres que se describen mejor con la especificación de efectos fijos. El valor del estadístico F supera al crítico (1.633), lo cual lleva a rechazar la hipótesis de que todas las entidades federativas comparten los mismos parámetros. A la vez, el estadístico Q del contraste de Hausman también es mayor que su valor crítico (3.841), indicando que la estimación por efectos fijos es preferible a la de aleatorios. Como el parámetro β_i es positivo y plenamente significativo, se puede afirmar que, durante el periodo 2000-2015, hubo divergencia en los porcentajes de población analfabeta de los estados de México.

El porcentaje de población de 15 años y más con educación básica incompleta tiene asociadas estimaciones positivas para el parámetro β_i en señal de divergencia. El valor del estadístico F lleva a rechazar el modelo de datos agrupados, mientras que el Q del contraste de Hausman revela que la estimación por efectos aleatorios presenta mejores propiedades. Esta es la única de las 11 variables del IRS en la que se prefiere la estimación con efectos aleatorios.

El porcentaje de población sin derechohabiencia a servicios de salud también muestra estimaciones positivas y significativas para el parámetro β_i. Sin embargo, el estadístico F no permite rechazar el modelo de datos agrupados, por lo que se está ante un caso de divergencia absoluta.

Lo mismo ocurre con el porcentaje de viviendas con piso de tierra, que también experimentó divergencia absoluta entre el 2000 y 2015.

Los porcentajes de viviendas sin excusado o sanitario y sin agua entubada presentan dinámicas similares. Los valores del estadístico F invitan a elegir el modelo de datos agrupados para el que ambas carencias muestran estimaciones positivas. La diferencia con los casos anteriores se encuentra en que estas carecen de significatividad, por lo que no es posible establecer una conclusión definitiva sobre su dinámica.

Para el porcentaje de viviendas que no disponen de drenaje, el estadístico F rechaza el modelo de datos agrupados y el Q indica que es preferible la estimación por efectos fijos frente a la de aleatorios. En esa situación, el parámetro tiene signo negativo con confianza de 99%, de manera que es posible afirmar que hubo convergencia en el porcentaje de viviendas sin drenaje, solo que esta fue condicionada ya que se obtiene con la especificación de efectos fijos, esto es, cada entidad convergió hacia un estado estacionario propio que dependía de sus características estructurales. Cabe recordar que este fenómeno, así como los procesos de divergencia, solo tiene sentido al considerar un lapso relativamente breve, de 15 años, como es el caso. En el largo plazo, en un horizonte ideal, las variables del IRS deben converger incondicionalmente hacia su mínimo y las carencias en cuestión, desaparecer, siguiendo la tendencia de continua reducción que vienen desarrollando.

El porcentaje de viviendas que no disponen de energía eléctrica tiene un estadístico F muy próximo a 0, que lleva a preferir el modelo de datos agrupados. El signo del parámetro estimado es negativo y significativo con confianza de 95%, indicando que se está ante un proceso de convergencia absoluta.

El porcentaje de viviendas que no disponen de lavadora también tendió a la convergencia, pero en la especificación condicionada, ya que el modelo que mejor describe su dinámica es el de efectos fijos.

Por último, no se advierte una evolución clara en el porcentaje de viviendas sin refrigerador. El valor del estadístico F lleva a elegir el modelo de datos agrupados, pero por estrecho margen respecto al de efectos fijos, obteniéndose una estimación carente de significación estadística.

A modo de resumen, se puede destacar que, de las 11 variables que integran el IRS, dos experimentaron convergencia absoluta durante el periodo 2000-2015 (población que no asiste a la escuela y viviendas sin energía eléctrica), dos más mostraron convergencia condicionada (viviendas sin drenaje y sin lavadora), otras dos registraron divergencia absoluta (población sin derechohabiencia a servicios de salud y viviendas con piso de tierra) y dos más, divergencia condicionada (población analfabeta y con educación básica incompleta). Hubo tres variables sin dinámicas de convergencia o divergencia significativas: viviendas sin excusado, sin agua entubada y sin refrigerador; las dos primeras con signos de divergencia y la última de convergencia.

Conclusiones

El cálculo de las tasas de variación reporta resultados sustancialmente distintos a los de las VA. Las entidades con más avances en la reducción de sus rezagos difieren de una medida a la otra. Si bien es cierto que las mayores variaciones absolutas se registraron en los estados con superiores niveles de carencias, también se debe advertir que las poblaciones con menores rezagos no disponían de margen de mejora para igualar esos progresos en esos términos. Como se ha explicado, medir la disminución de las carencias en VA implica asumir un sesgo en favor de las entidades que presentan valores más altos, ya que, simplemente por ello, les es posible experimentar mayores avances.

Las tasas de variación, sin embargo, no presentan un sesgo a priori para la medición del abatimiento de los rezagos, que siempre pueden reducirse desde 0 hasta 100%; esta otra medida no identifica a las entidades más rezagadas con las de mayores avances o, al menos, no en todos los casos. Los análisis de convergencia señalan algunas variables y periodos en que los estados más rezagados disfrutaron de mayores reducciones de ciertas carencias. No obstante, predominan los casos de divergencia y convergencia condicionada.

Este nuevo escenario no da lugar a la contradicción que se crea al anunciar que los estados más rezagados progresaron más que el resto en el abatimiento de sus carencias, al tiempo que el IRS, calculado a partir de esos mismos datos, no muestra ningún estrechamiento de la brecha que separa a Guerrero, Oaxaca y Chiapas de los otros (ver gráfica), sino incluso un leve ensanchamiento de esa distancia. El caso es que no hubo una convergencia generalizada en las variables componentes del IRS. Las entidades más rezagadas progresaron mejor que las avanzadas en algunas variables, pero no en otras, ni a lo largo de todo el periodo de análisis, por lo que su posición relativa apenas varió, lo mismo que la brecha en el IRS.

La descripción que se consigue con las variaciones absolutas no es tan coherente con la dinámica del IRS a lo largo del tiempo como la de las tasas de variación. Además, la primera medida padece el sesgo mencionado: permite superiores avances en las unidades territoriales con más rezagos. Por ello, la conclusión de que “…aquellas entidades que han mostrado las mayores disminuciones son también los estados con los mayores niveles de rezago social…” (CONEVAL, 2016a: 10) parece un tanto precipitada, ya que no valora los resultados de otras medidas con mejores propiedades para ese análisis.

La variedad de resultados obtenidos plantea incógnitas que hasta el momento no se estaban considerando. Lo principal a partir de ahora, tal vez, sea conocer por qué unas variables convergen y otras no, esto es, cuáles son las causas de esas dinámicas diferentes, ya que ni siquiera los indicadores de una misma dimensión evolucionan igual. El ejemplo más claro es el de las variables de educación, donde el porcentaje de población de 6 a 14 años que no asiste a la escuela tendió a converger, mientras que hubo divergencia interestatal en la analfabeta y en la población con educación básica incompleta. El hecho de que la convergencia se diera en la variable que posiblemente es más fácil de modificar a corto plazo es un indicio a seguir para futuras investigaciones que profundicen en el tema, pero también recuerda una limitación básica de este tipo de análisis: los procesos de cambio estructural y divergencia-convergencia son fenómenos de largo plazo, por lo que sería deseable disponer de datos para un periodo más amplio que los 15 años considerados en este.

________________

Fuentes

Aparicio, R. Índice absoluto de marginación, 1990-2000. México, Consejo Nacional de Población, 2004.

Banco de México. “Recuadro 1. Convergencia regional en México: 1994-2015”, en: Reporte sobre las economías regionales. Enero-marzo, 2017, pp. 5-8.

Barro, R. J. y X. Sala-i-Martin. “Economic growth and convergence across the United States”, en: National Bureau of Economic Research Working Paper Series, 3419, 1990 (DE) https://bit.ly/39wYGgu, consultado el 31 de julio de 2018.

Campos, R. M., C. Domínguez y G. Márquez. “Long-run human development in Mexico: 1895-2010”, en: L. Bértola y J. Williamson (eds.). Has Latin American inequality changed direction? Looking over the long run. Cham, Springer, 2017, pp. 89-112.

CONEVAL. Los mapas de pobreza en México. México, 2007 (DE) https://bit.ly/2x80rSY, consultado el 10 de febrero de 2019.

_______ Índice de Rezago Social 2015. Presentación de resultados. México, 2016a (DE) https://bit.ly/3909RgE, consultado el 15 de enero de 2019.

_______ Índice de Rezago Social 2015 a nivel nacional, estatal y municipal. México, 2016b (DE) https://bit.ly/2PWopYe, consultado el 30 de diciembre de 2016.

_______ ¿Quiénes somos? México, 2019 (DE) https://bit.ly/394aSEN, consultado el 12 de febrero de 2019.

Diario Oficial de la Federación (DOF). Ley General de Desarrollo Social. 20 de enero de 2004.

Gutiérrez, H. y V. Gama. “Limitantes de los índices de marginación de CONAPO y propuesta para evaluar la marginación municipal en México”, en: Papeles de Población. 66, 2010, pp. 227-257.

Hausman, J. A. “Specification tests in econometrics”, en: Econometrica. 46(6), 1978, pp. 1251-1271.

Juan, V. H. y L. A. Rivera. “Regional growth in Mexico: 1970-93”, en: IMF Working Paper. 92, 1996.

Luna, N. R. y R. Colín. “Crecimiento económico y convergencia regional en México 1970-2015”, en: Economía y Sociedad. 21(36), 2017, pp. 77-95.

Martín-Mayoral, F. y J. Yépez. “Evolución de las disparidades en el desarrollo económico y humano de América Latina: análisis del IDH y sus com­ponentes”, en: Economía Mexicana Nueva Época. 1, 2013, pp. 203-246.

Peláez, Ó. “Dependencia temporal y convergencias sincrónica y diacrónica en el IDH de las entidades federativas de México, 1950-2010”, en: Premio Eliseo Mendoza al Análisis Económico del Desarrollo Regional. 2017 (DE) https://bit.ly/3daiTee, consultado el 14 de julio de 2019.

Programa de las Naciones Unidas para el Desarrollo (PNUD). Informe sobre desarrollo humano México 2002. México, Mundi-Prensa, 2003.

Rodríguez, L. I. y J. A. Cabrera. “Convergencia municipal en México con modelos de econometría espacial (1999-2014)”, en: EconoQuantum. 16(1), 2019, pp. 7-32.

Ruiz, C. “Desigualdades regionales en México, 1900-1993”, en: Estudios Demográficos y Urbanos. 11(3), 1997, pp. 572-576.

Sen, A. “Public action and the quality of life in developing countries”, en: Oxford Bulletin of Economics and Statistics. 43(4), 1981, pp. 287-319.

Yang, F., S. Pan y X. Yao. “Regional convergence and sustainable develop­ment in China”, en: Sustainability. 8(121), 2016, pp. 1-15.

^[1] Específicamente, Aparicio (2004: 28) explica que “…durante la última década del siglo XX las mayores reducciones absolutas en el índice absoluto de marginación tuvieron lugar en los estados más marginados, lo que ha tenido como consecuencia una importante disminución de la desigualdad entre las entidades federativas en el ámbito de la marginación…”. En el PNUD (2003: 61-2) se menciona que “…Mientras que en 1950 el máximo logro en este índice era de 0.5356 –Distrito Federal– y el mínimo era de 0.3197 –Chiapas–, en 2000 el máximo fue de 0.8394 para Baja California y el mínimo de 0.7881 para Chiapas. Lo anterior significa que la diferencia se redujo entre los extremos de aproximadamente 67% a menos de 7%…”.

^[2] Hoy la Ciudad de México.

^[3] En caso de registrarse un aumento en el valor de alguna variable, este también se interpreta en términos porcentuales respecto al valor observado al inicio del periodo de análisis.