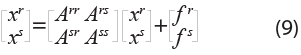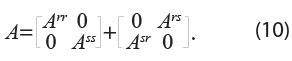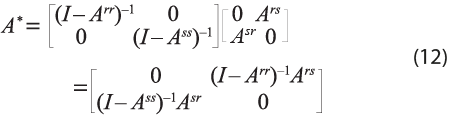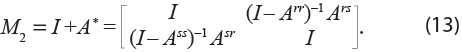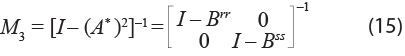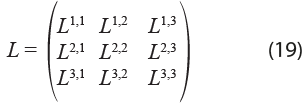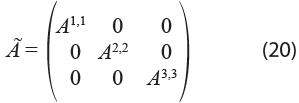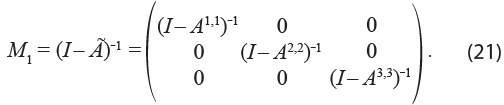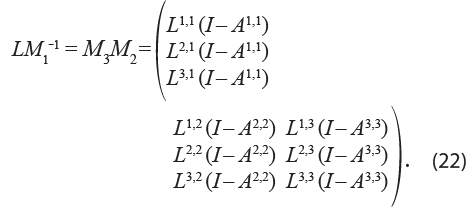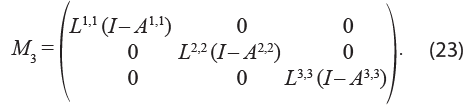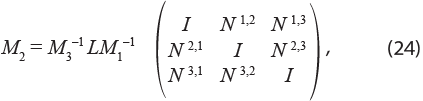Análisis de la descomposición estructural de la matriz insumo-producto multiestatal de México 2013: efectos intrarregionales, de desbordamiento y de retroalimentación

Analysis of the Structural Decomposition of Mexico's Multistate Input-Output Matrix 2013: Intraregional, Interregional, and Feedback Effects

 

Víctor Hugo Hernández García,* Mario Alberto Mendoza Sánchez** y José Valentín Solís y Arias*
* Instituto Nacional de Estadística y Geografía (INEGI), victor.garcia@inegi.org.mx y valentin.solis@inegi.org.mx, respectivamente.
** Universidad de Sonora, mario.mendoza@unison.mx.

 

Vol. 15, Núm. 1 - Epub                                            Análisis de la descomposición...  -Epub  

 

El objetivo de este artículo es realizar un análisis de la descomposición estructural de las matrices insumo-producto multiestatales de México 2013; para ello, se utiliza la técnica de descomposición aditiva de Stone (1985), que separa a la matriz inversa de Leontief en tres componentes: impactos intrarregionales, de desbordamiento y de retroalimentación. Se propone una generalización del procedimiento de descomposición que permite considerar matrices con más de dos regiones. Los resultados, presentados para siete zonas del país, indican que los efectos interregionales sobre el volumen de producción bruta oscilan entre 7.28 y 19.94 %, que varían en función del tamaño económico de las regiones estudiadas. Se enfatiza que las interdependencias regionales son importantes según el nivel de desarrollo de las áreas geográficas delimitadas. Palabras clave: descomposición estructural; modelo interregional; matrices insumo-producto multirregionales.

The objective of this article is to carry out an analysis of the structural decomposition of the multi-regional Input-Output Matrices of Mexico 2013. For this, the additive decomposition technique of Stone (1985) is used. It separates the inverse Leontief matrix into three components: intraregional, interregional and feedback impacts. A generalization of the decomposition procedure is proposed, since that allows analyzing matrices with more than 2 regions. The results, presented for 7 regions of the country, indicate that the interregional effects on the volume of gross production oscillate between 7.28 and 19.94 percent, which vary depending on the economic size of the regions studied. It is emphasized that regional interdependencies are important according to the level of development of the regions. Key words: structural decomposition; interregional model; multi-regional input-output tables.

Recibido: 8 de junio de 2023.
Aceptado: 1 de septiembre de 2023.

 

Introducción

En la literatura relacionada con el estudio de la economía mexicana se ha posicionado una creciente atención en el análisis regional a través de los modelos multisectoriales basados en matrices insumo-producto (MIP) que estudian las estructuras económicas en escala subnacional. De acuerdo con Isard (1951), el interés en esta línea de investigación surge, principalmente, por la necesidad de cuantificar relaciones de interdependencia sectorial de las ramas económicas que interactúan en la dimensión geográfica.

El desarrollo de este tipo de estudios implica dos desafíos fundamentales: el primero se relaciona con la construcción y/o elaboración de las cuentas económicas estatales desde la perspectiva multisectorial y el segundo, con el tipo de análisis que se desarrolla una vez construidas; así lo documentan los trabajos de investigación en México: Albornoz et al. (2021), Alvarado et al. (2019), Amaral et al. (2020), Asuad (2020), Chapa (2020), Chapa y Ayala (2020), Chiquiar et al. (2017), Dávila et al. (2015), Dávila y Valdés (2020), Fuentes et al. (2018), Gaytán y Vargas (2019) y Torre et al. (2017), entre otros.

Recientemente, el Instituto Nacional de Estadística y Geografía (INEGI) publicó un conjunto de MIP estatales y multiestatales para el 2013 (INEGI, 2022), las cuales constituyen una fuente de información básica para el estudio del sistema regional mexicano desde una perspectiva multisectorial. Representa un avance significativo para la construcción del sistema de cuentas estatales, ya que incluye MIP para cada una de las 32 entidades federativas del país, así como todas las matrices de comercio bilateral interestatal, por lo que se puede analizar el origen y destino de la producción de cada estado. Cabe precisar que esta publicación, de corte experimental, se encuentra entre los pocos estudios relacionados con la construcción de sistemas de cuentas multiestatales en México, entre los que destacan el Sistema Interregional de Insumo-Producto Ajustado (IIOAS, por sus siglas en inglés) propuesto por Amaral et al. (2020), el enfoque híbrido (top-dow botom-up) de Asuad (2020) y el método clásico de Flegg empleado por Dávila et al. (2015).  

De manera analítica, el estudio estructural de sistemas multirregionales puede resultar trivial cuando los efectos económicos de una región hacia otra no son importantes, así lo constataron las primeras investigaciones sobre el tema (Miller, 1966, citado en Miller y Blair, 2022). No obstante, los impactos interregionales pueden ser muy distintos en función del tamaño del espacio económico estudiado y su capacidad para suministrar todos los insumos necesarios para habilitar el funcionamiento de su estructura productiva. En este contexto, este documento busca responder la pregunta: ¿qué tan significativos son los efectos multiplicadores interregionales en México? La hipótesis de este trabajo sostiene que, dada la heterogeneidad estructural y regional al interior de la economía mexicana, aquellos ocasionados por vía de la demanda son altos en regiones menos desarrolladas y bajos en las de mayor desarrollo económico.

Para resolver esta pregunta, planteamos el uso de la descomposición multiplicativa de Pyatt y Round (1979), así como su extensión aditiva propuesta por Stone (1985). Con esta técnica, es posible descomponer los efectos de un impacto económico, como puede ser un aumento de las exportaciones, por ejemplo, inducidas intrarregionalmente (en la propia región), de desbordamiento (sobre otras zonas) y de retroalimentación (que salieron de una región, pero que de manera eventual regresan). A pesar de la popularidad de estas técnicas en el estudio de matrices insumo-producto, el día de hoy han tenido la limitación de poder usarse con claridad analítica en modelos con solo dos regiones económicas. Cuando los mismos pasos propuestos por Pyatt y Round se aplican en matrices con tres o más, la interpretabilidad de los resultados deja de ser intuitiva (Hewings, 1985: 51).

A pesar de ello, estas técnicas han tenido también éxito en el estudio de matrices de contabilidad social para analizar la interacción entre sectores económicos e institucionales, y factores de la producción, como se muestra en Pyatt y Round (1979) o Defourny y Thorbecke (1984) y otros trabajos que de ahí se desprenden. Aunque en estas investigaciones se realiza la descomposición en matrices particionadas en tres bloques, se trata de un caso muy particular en el que estos interactúan entre sí en la forma de un circuito cerrado (Round, 1985), es decir, los sectores económicos solo generan pagos a los factores, estos únicamente pagan a las instituciones y estas solo liquidan a los sectores.

Cuando la matriz analizada tiene estas características, la descomposición multiplicativa de Pyatt puede aplicarse sin problemas interpretativos, pero este no es el caso de una de comercio interregional donde, potencialmente, todas las regiones interactúan con las demás. Por ello, en este trabajo proponemos una modificación al procedimiento de Pyatt que permite obtener tres matrices en las cuales la interpretación de los impactos intrarregionales, de desbordamiento y de retroalimentación son idénticos a la original, pero es aplicable a matrices con cualquier número de particiones regionales.

En México, son pocos los estudios que realizan análisis estructural con base en un marco contable multirregional; entre ellos se encuentra Dávila et al. (2015) y Fuentes et al (2018). En el mejor conocimiento de los autores, solo el primero emplea el análisis de descomposición con un modelo birregional. Para este trabajo, se utiliza uno multirregional agrupado en siete regiones. De aquí que una contribución de la investigación es que representa el primer ejercicio en el país que realiza un análisis de descomposición estructural para más de dos regiones.

Después de esta introducción, el segundo apartado presenta la formulación matemática del modelo multirregional en su versión más simple con dos regiones; el tercero describe las características de las MIP multiestatales 2013 como fuente de información estadística; en el cuarto se presenta la metodología relacionada con las técnicas de la descomposición estructural; en el quinto se muestran los resultados y principales hallazgos; finalmente, se anotan las conclusiones.

 

Matrices multiestatales de México 2013

Las cuentas económicas estatales que se utilizaron en esta investigación fueron obtenidas de la reciente publicación del INEGI (2022) de los cuadros de oferta y utilización (COU) y las MIP a nivel estatal del 2013.^[1] La valoración de estos se expresa en millones de pesos corrientes de ese año; se consideró una desagregación sectorial de 32 actividades económicas y 79 subsectores que tienen como referencia el Sistema de Clasificación Industrial de América del Norte (SCIAN).

La estimación de estas matrices partió de los COU nacionales con una desagregación de 262 ramas de actividad económica. La principal fuente de información a nivel estatal es el Producto Interno Bruto Estatal (PIBE) del 2013, el cual se publica desagregado en 32 actividades basadas en el SCIAN, por lo cual es la restricción más importante para el detalle de las industrias. Se aprovecharon indicadores obtenidos de los Censos Económicos 2014^[2] para estimar ponderadores específicos por estado para la agregación. Por ejemplo, si para obtener una de las 32 actividades se tienen que agregar ocho ramas del SCIAN, los pesos de estas en el proceso deben ser distintos para cada entidad. Esto da como resultado técnicas de producción (coeficientes técnicos) diferenciados que reflejan la especialización productiva del estado en cuestión.

Para la estimación de la demanda final (DF) estatal, se contemplaron insumos adicionales, como la Encuesta Nacional de Ingresos y Gastos de los Hogares (ENIGH) del INEGI, información sobre la producción de los gobiernos estatales y locales y la inversión extranjera directa por sector y estado; estos sirvieron de apoyo para calcular los consumos privado y de gobierno, así como la formación bruta de capital, respectivamente. La desagregación de estas fuentes permitió obtener la DF con un detalle de 79 subsectores de actividad SCIAN.

Para distinguir el origen de los productos, se empleó el coeficiente de localización de Flegg, el cual permite distinguir si los bienes y servicios son producidos en el interior del estado o si proceden del resto del país, consideración que es aplicable tanto a los flujos de comercio de transacciones intermedias como de demanda final. Posteriormente, se aplicó un modelo gravitacional para establecer las entidades de origen y destino de los bienes y servicios que definen el comercio entre entidades federativas.

Para consolidar los registros estimados en los COU estatales en el marco de los COU nacionales, se ha aplicó la técnica RAS Generalizado Multirregional (MR-GRAS, por sus siglas en inglés). Esta garantiza que la suma de los cuadros estatales y de comercio sea igual que el COU total a nivel nacional, coeficiente por coeficiente, además de balancear los flujos de bienes y servicios por el lado de la oferta y la demanda entre regiones. Como resultado, los COU estatales y el multiestatal son perfectamente consistentes con la información a nivel nacional y entre sí.

Por último, una vez balanceados los COU estatales, se emplearon las recomendaciones del manual de la Oficina de Estadística de las Naciones Unidas sobre modelos estándar para realizar la transformación de los COU en MIP simétricas. Como resultado, se obtuvieron matrices producto por producto e industria por industria con dimensiones 2 528 x 2 528 y 1 024 x 1024, respectivamente.

 

Modelo multirregional de insumo-producto

Elaborar las MIP multirregionales implica desarrollar el modelo de Walter Isard (1951) para incorporar el componente espacial dentro del insumo-producto (IP). Aquí se presenta la versión más simple del modelo multirregional con solo dos regiones y  actividades económicas: la región r y la s. El vector de producción bruta birregional de dimensión 2n × 1 representado por x^br es como sigue:

donde la producción bruta de las regiones r y s está representado, respectivamente, por x^r y x^s, cada uno de dimensiones n × 1. Siguiendo el modelo de insumo-producto de Leontief, el sistema se puede expresar en forma matricial de la siguiente manera:

x^br = Z^br + f^br                                 (2)

donde Z^br, de dimensiones n × r, representa la matriz de transacciones intersectoriales de las regiones r y s, que incluye los flujos de comercio intra e interregionales, y f^br es el vector de DF birregional, de dimensiones n × 1. La matriz de transacciones intersectoriales Z^br se puede particionar en:

 

 

donde las submatrices de n × n, Z^rr, y Z^ss, representan las transacciones intersectoriales e intrarregionales de las regiones r y s, respectivamente, y las Z^rs y Z^sr son las matrices de comercio intersectorial e interregional de producción de r vendida a s, y viceversa. Por su parte, el vector de demanda final birregional es:

 

donde f^r y f^s representan la DF de producción de las regiones r y s, respectivamente, de dimensiones n × 1. A su vez, la matriz de coeficientes técnicos es:

 

donde A^rr y A^ss son submatrices de coeficientes técnicos intrarregionales de las regiones r y s, respectivamente, y A^rs y A^sr son submatrices de coeficientes de importaciones de insumos producidos en r y demandados por s, y viceversa; todas de dimensión n × n. Utilizando la definición de coeficientes técnicos  , se sustituye (5) en (2):

 

x^br = A^br x^br + f^br                                             (6)

Despejando el vector de demanda final birregional se tiene:

Considerando  y la matriz de identidad  la solución es:

 

 

donde [I^br - A^br]^-1 se conoce como la matriz inversa de Leontief (L^br) para un modelo birregional, de dimensiones 2n × 2n. Esta solución incluye los efectos que se obtendrían de uno de una región simple, y los aumenta por los flujos de comercio interregional, como se demuestra en Miller y Blair (2022, p. 72). En síntesis, la solución establece que la producción bruta se encuentra determinada por el nivel de DF en ambas regiones, así como por las matrices de coeficientes técnicos intrarregionales y de comercio interregional.

 

Técnica de descomposición estructural en MIP de dos regiones

Inicialmente, su análisis fue desarrollado en el marco de matrices de contabilidad social en la formulación multiplicativa establecida por Pyatt y Round (1979); después, se realizó la formulación aditiva propuesta por Stone (1985). Dadas las propiedades de estas, se aplicaron también al modelo insumo-producto regional.

En el caso de la descomposición multiplicativa, el objetivo es separar la matriz inversa de Leontief en tres matrices que den cuenta de los efectos intrarregionales (M₁), de desbordamiento (M₂) y de retroalimentación (M₃) que se dan en el marco de una economía con circularidad, donde los choques se mueven por la cadena de producción y pueden volver al sector y región de origen, de forma que esta se exprese como L = M₃ M₂ M₁, todas matrices de dimensiones 2n × 2n.

En esta sección se muestra el procedimiento tradicional para descomponer matrices birregionales y, posteriormente, se presenta la generalización para aquellas con tres o más regiones. Si se especifica este modelo en su forma simple de dos se tiene:

 

Para capturar los efectos intrarregionales M₁, se separa la matriz de coeficientes técnicos en dos matrices:

 

 

Si se define  como la matriz de coeficientes técnicos intrarregionales, entonces, la de Leontief asociada es , por lo que la solución para este componente se expresa como:

 

 

Las submatrices sobre la diagonal principal corresponden con la inversa de Leontief, o matriz de multiplicadores contables, que se obtendrían para cada región sin considerar los flujos interregionales, es decir, los modelos individuales de las dos regiones.

Por otra parte, para la medición de los efectos de desbordamiento M₂, derivados del comercio interregional, se define A^* = (I - Ã)^-1 (A - Ã)  como la matriz de coeficientes de comercio interregional; su especificación se realiza como sigue:

 

 

por lo que su solución resulta como sigue:

Este término de la descomposición incluye a la matriz identidad, que al multiplicarse por M₁ reflejará el choque en la región inicial, y la matriz A^*, la cual representa el impacto que se traslada de una región a otra de forma directa. Es decir, esta es el impacto del comercio interregional dado un choque que, por ejemplo, inicia en la región r y que demanda insumos a la s.

Finalmente, para capturar efectos de retroalimentación M₃, se define:

 

donde B^rr = (I - A^rr)^-1 A^rs (I - A^ss)^-1 A^sr y B^ss = (I - A^ss)^-1 A^sr (I - A^rr)^-1 A^rs

Entonces, la solución es:

 

Esta matriz captura el impacto de un choque que, por ejemplo, inicia en la región r, viaja a la s y, finalmente, regresa a la de origen r, donde a su vez generará nuevos efectos multiplicadores. Es por este motivo que a esta matriz también se le conoce como la de efectos de bucle cerrado (closed loop). En resumen, M₁ permite capturar los impactos intrarregionales por causa de las transacciones que se dan en cada una las regiones (inversa de Leontief), y las matrices M₂ y M₃ registran los impactos interregionales por efectos de desbordamiento (spillover effects) y de retroalimentación (feedback effects) del comercio entre regiones, respectivamente (Miller y Blair, 2022: 378). Por lo tanto, la solución del modelo multirregional en su esquema básico es:

 

x = M₃ M₂ M₁ f                                      (16)

 

A pesar de que la forma algebraica de esta descomposición hace evidente el significado de cada una de las matrices, la interpretación numérica de sus elementos se vuelve confusa para los analistas. Por ejemplo, para interpretar un valor en la matriz M₃, se debe considerar el múltiplo de las dos matrices previas. Por este motivo, es más común presentar los resultados siguiendo la versión aditiva, cuya lectura es más directa e intuitiva.

La descomposición aditiva toma como base las matrices obtenidas de la multiplicativa, y se expresa de la siguiente manera:

 

L = I + (M₁ – I) + (M₂ – I) M₁ + (M₃ – I) M₂M₁                        (17)

 

Con la matriz inversa de Leontief descompuesta en estos cuatro términos aditivos, calculamos la producción bruta total como:

 

x = If + (M₁ – I) f + (M₂ – I) M₁ f + (M₃ – I) M₂M₁f                        (18)

 

Siguiendo la lógica de las particiones establecidas en la formulación multiplicativa, el impacto inicial se establece en If, el efecto neto intrarregional se contempla en (M₁ – I) f , el choque neto interregional por efectos de desbordamiento se captura en (M₂ – I) M₁ f y el neto por retroalimentación se registra en (M₃ – I) M₂M₁f  (Miller y Blair, 2022: 379).

 

Técnica de descomposición estructural en MIP de tres o más regiones

Es importante señalar que este método, hasta ahora, se utiliza en dos contextos muy específicos: en matrices particionadas en solo dos regiones y en las de contabilidad social, cuya estructura forma un circuito cerrado (Pyatt y Round, 1979). Cuando los pasos de esta metodología se aplican en matrices con tres o más particiones, el resultado de M₂ y M₃ tiene una interpretación menos clara (Hewings, 1985: 51). Para M₂ aparecen elementos sobre la diagonal principal, por lo que no puede interpretarse como efectos únicamente de desbordamiento, mientras que para M₃ hay elementos fuera de esta, y por ello no es posible leerse como efectos de circuito cerrado (choques que terminan donde iniciaron). No es el caso cuando se aplica en matrices de contabilidad social, que suelen estar particionadas en tres secciones (industrias, factores de la producción e instituciones), cuya estructura forma un circuito cerrado.

En este trabajo utilizamos una técnica alternativa para obtener M₂ y M₃ con el objetivo de preservar la claridad analítica de las interpretaciones en el contexto de matrices multiestatales. Esta puede aplicarse a matrices con cualquier número de regiones, pero se ejemplifica para el caso de solo tres. Por lo tanto, en un modelo con R regiones, las matrices L, M₁, M₂ y M₃ tienen dimensiones Rn × Rn. Sea la matriz inversa de Leontief del modelo multirregional:

 

 

Sabemos que la matriz M₁ debe capturar únicamente los efectos intrarregionales, los cuales se obtienen de los modelos independientes de cada una de las tres regiones. Por lo tanto, la definimos como:

 

 

Así, la matriz de coeficientes técnicos de transacciones intrarregionales y su respectiva inversa de Leontief son como sigue:

 

 

Si postmultiplicamos la matriz L = M₃M₂M₁ por la inversa de M₁ obtenemos:

Dado que buscamos reproducir la propiedad de M₂ conformada por matrices identidad sobre la diagonal principal y queremos que M₃ solo tenga valores sobre los bloques de la diagonal principal, podemos concluir que M₃ debe estar definida como la matriz diagonal de la ecuación (22):

 

 

Lo anterior tiene sentido pues, si analizamos uno de los términos sobre la diagonal L^1,1 (I – A^1,1) L^1,1 - L^1,1 A^1,1, el primer elemento representa el multiplicador total del sistema multirregional y el segundo, solo los impactos de la demanda intrarregional. El resultado de esta resta es el impacto que el comercio interregional originado en la región 1 tiene sobre esta misma.

Por lo tanto, si despejamos la matriz M₂ de la expresión (22), tenemos que:

 

 

Donde N^ij = (I – A^i,i)^-1 (L^i,i)^-1 L^ij (I -A ^jj).  Esta cumple con las propiedades que buscamos, y en este trabajo proponemos su interpretación como los efectos de desbordamiento del sistema, o interregionales. El lector puede corroborar que, al aplicar estas operaciones en matrices con dos regiones, se obtienen los mismos resultados que en la descomposición multiplicativa de la sección anterior.

Una vez lograda esta descomposición multiplicativa, la aplicación de la aditiva de Stone se realiza de forma directa, de modo que sus partes mantienen las mismas propiedades e interpretaciones.

 

Descripción y análisis de resultados

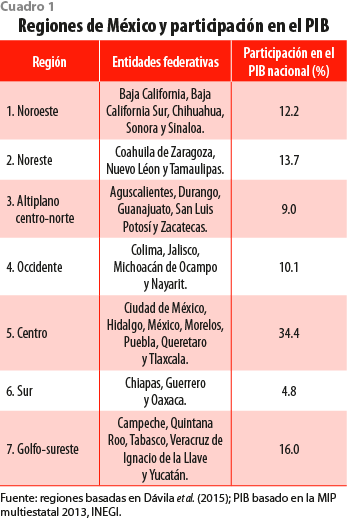
Antes de realizar los primeros tratamientos de descomposición estructural del modelo insumo-producto multiestatal, es necesario precisar las regiones que serán consideradas. Este trabajo se ciñe a la regionalización establecida por Dávila et al. (2015) quienes definen siete mesorregiones mexicanas: noroeste, noreste, altiplano centro-norte, occidente, centro, golfo-sureste y sur. En el cuadro 1 se presentan las entidades que conforman cada una de estas, mientras que el mapa muestra su distribución geográfica.

 

 

 

 

Los criterios de regionalización que los autores consideran son los siguientes: contigüidad geográfica, exclusividad, distancia respecto a la frontera norte y condiciones geográficas relevantes, específicamente la localización relativa de las entidades con respecto a las principales cadenas montañosas y a los litorales. Como se observa en el cuadro 1, una tercera parte del PIB nacional se concentra en la región centro, mientras que la sur tiene una aportación muy modesta en comparación con el resto.

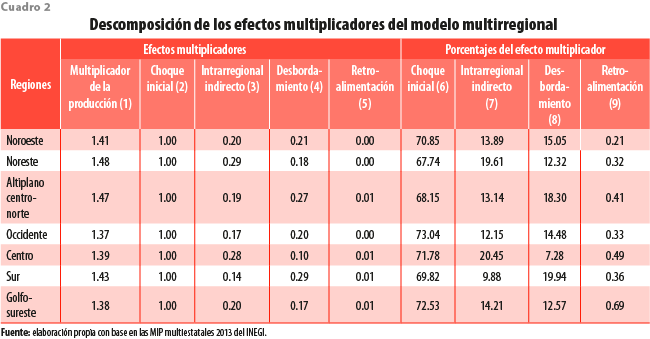
Una vez establecidas las regiones a estudiar, los resultados de la descomposición aditiva de Stone se presentan en el cuadro 2. La columna (1) muestra el multiplicador total; de la (2) a la (5) se descompone el valor de multiplicador en efectos directos, indirectos (intrarregionales), de desbordamiento y de retroalimentación (interregionales); y en las (6) a la (9) se expresan los mismos valores como porcentaje del multiplicador de la producción, de forma que suman 100.

 

 

En la columna (1) se presenta el multiplicador de la producción total por región de estudio. Este se refiere al promedio ponderado de los multiplicadores sectoriales, donde los ponderadores son proporcionales a la demanda final de la región. Por ejemplo, el multiplicador de 1.48 de la noreste indica que un aumento de 1 millón de pesos en la demanda de productos de esta región resulta en un incremento de 1.48 millones de pesos en la producción bruta de todo el país; de este monto, 1 millón es el valor de los bienes demandados (choque inicial), 290 mil pesos equivalen a insumos indirectos producidos ahí (efecto intrarregional indirecto), 180 mil son producidos por otras regiones que le proveen insumos (de desbordamiento) y el monto restante es la producción en la noreste que se requiere para producir insumos en otras zonas (de retroalimentación). Las regiones noreste y altiplano centro-norte muestran el valor del multiplicador más alto con 1.48 y 1.47, respectivamente, seguidas por la sur y noroeste con 1.43 y 1.41, en ese orden. Al final se encuentran la centro, golfo-sureste y occidente con indicadores de 1.39, 1.38 y 1.37.

En términos porcentuales, en la columna (6) se observa que los choques iniciales dominan la mayor parte del efecto multiplicador con un valor que gira alrededor de 70 % la región occidente es la que muestra un mayor efecto inicial con 73.04 %, seguida por la golfo-sureste, centro y noroeste con 72.53, 71.78 y 70.85 %, respectivamente; por último, la sur, altiplano centro-norte y noreste tienen los menores efectos iniciales con 69.82, 68.15 y 67.74 %, en ese orden. Un porcentaje alto del efecto multiplicador en el choque inicial está relacionado en contraparte con menores efectos indirectos, de desbordamiento y de retroalimentación, es decir, si el primero es elevado, los segundos tienen que ser bajos debido a que no hay requerimientos de insumos para el resto de las cadenas de producción. El caso extremo sería un producto que se extrae de manera directa de la tierra (sin necesidad de insumos) y así se vende a los consumidores, por lo que el choque inicial sería 100 % del impacto.

En lo referente a los efectos intrarregionales indirectos, se destaca en la columna (7) que la centro y noreste tienen los mayores valores con 20.45 y 19.61 %, respectivamente. Esto indica que estas son economías con cadenas de producción más articuladas hacia el interior, esto es que, ante una inyección exógena en la demanda final, se generan compras indirectas de insumos hacia otras actividades localizadas en la región. En contraposición, la sur tiene un indicador de 9.88 % lo que genera menos efectos indirectos hacia el interior de su economía y refleja una alta dependencia de insumos intermedios importados de otras zonas del país.

Por su parte, los efectos interregionales por impactos de desbordamiento se presentan en la columna (8). La forma de interpretar estos resultados es que cuando aumenta la DF en una región específica, esta ejerce demanda de insumos en otras. Los valores de desbordamiento son significativos para todas las regiones. La sur cuenta con los mayores efectos con 19.94 %, seguida por la altiplano centro-norte, noroeste y occidente con 18.30, 15.05 y 14.48 %, respectivamente. Por último, la golfo-sureste, noreste y centro tienen indicadores de 12.57, 12.32 y 7.28 por ciento. Estas regiones podemos catalogarlas como poco dependientes del resto del país.

Finalmente, los efectos de retroalimentación se presentan en la columna (9), los cuales resultan ser muy bajos en todos los casos. La región golfo-sureste tiene el registro más alto con 0.69 %, seguida por la centro, altiplano centro-norte y sur con 0.49, 0.41 y 0.36 %, respectivamente. Al final, se encuentran la occidente, noreste y noroeste con 0.33, 0.32 y 0.21 %, en ese orden. Esto refleja que existe poca circularidad de los choques de demanda a este nivel de agregación regional, es decir, una vez que el impacto sale de la región de origen, prácticamente ha terminado de beneficiar a dicha región.

Estos resultados han permitido identificar que las regiones centro y noreste son las economías con mayor capacidad para hacer funcionar sus aparatos productivos, ya que cuentan con mayor proveeduría interna y tienen menos interdependencias de otras zonas del país. En cambio, la sur, como, situación contrapuesta, cuenta con una estructura menos articulada y más dependiente del resto de México. Los casos de la altiplano centro-norte, occidente, noroeste y golfo-sureste muestran estructuras más balanceadas entre su capacidad interna y sus interdependencias interregionales.

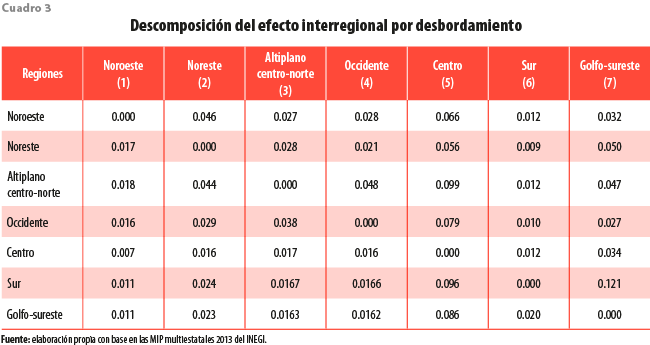
Con el propósito de identificar los efectos interregionales más significativos, el cuadro 3 presenta cómo se distribuyen los impactos a través de las regiones, donde la suma de los elementos sobre cada fila es igual a los efectos de desbordamiento —columna (4) del cuadro 2— esto muestra una manera de identificar los efectos interregionales más significativos entre cada una de las regiones analizadas.

 

 

La región noreste presenta un multiplicador total de 1.48 por cada cambio unitario en la demanda final; de este efecto total, 0.18 corresponde al interregional por desbordamiento hacia el resto de las regiones. En el cuadro 3 se observa que el interregional más alto de la noreste se establece con la centro y golfo-sureste con 0.056 y 0.050, respectivamente. A estas le siguen la altiplano centro-norte, occidente, noroeste y sur, con valores de 0.028, 0.021, 0.017 y 0.009, en ese orden.

Destacamos que la región centro es la que absorbe los principales efectos de desbordamiento. Esto puede explicarse por la alta concentración de servicios en Ciudad de México, como los financieros y profesionales,  además de actividades comerciales. A su vez, esta produce desbordamientos principalmente a la golfo-sureste.

En general, el cuadro 3 muestra que la cercanía geográfica es importante para determinar los efectos de desbordamiento. Lo observamos con los casos de la noroeste hacia la noreste y de la occidente hacia la altiplano centro-norte o de la región sur con altos desbordamientos hacia la golfo-sureste.

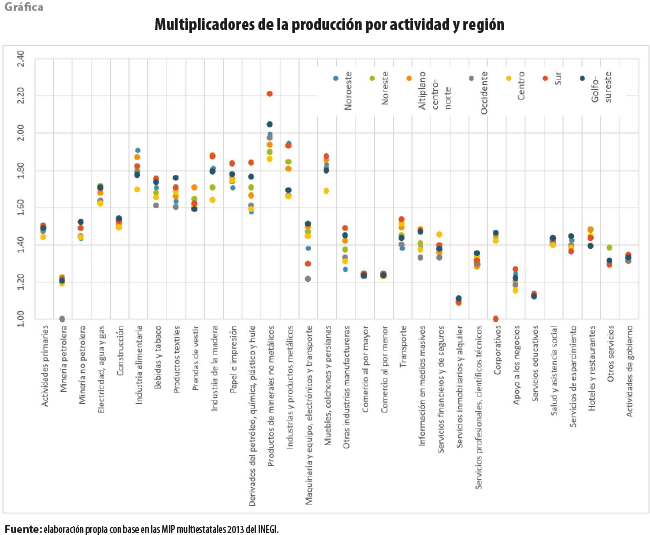
Una vez establecido el análisis de la descomposición estructural en la perspectiva interregional de desbordamiento, a continuación se presentan los efectos multiplicadores desde la multisectorial. La gráfica muestra el valor de los multiplicadores de la producción de cada una de las regiones. Se destaca que algunas actividades presentan una variación significativa a través de estas. Esto es resultado del proceso de construcción de las MIP multirregionales, donde las técnicas de producción están basadas en ponderadores específicos por estado, calculados de los Censos Económicos 2014.

 

 

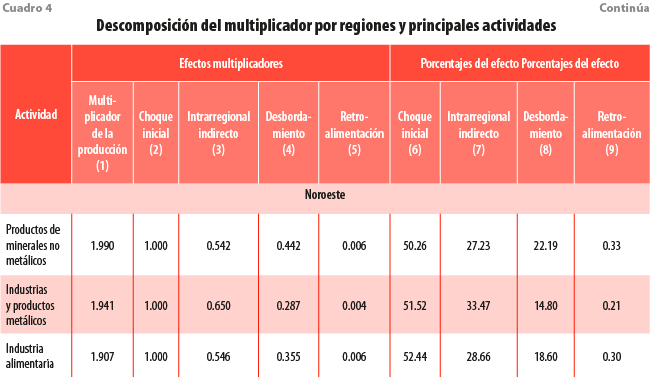
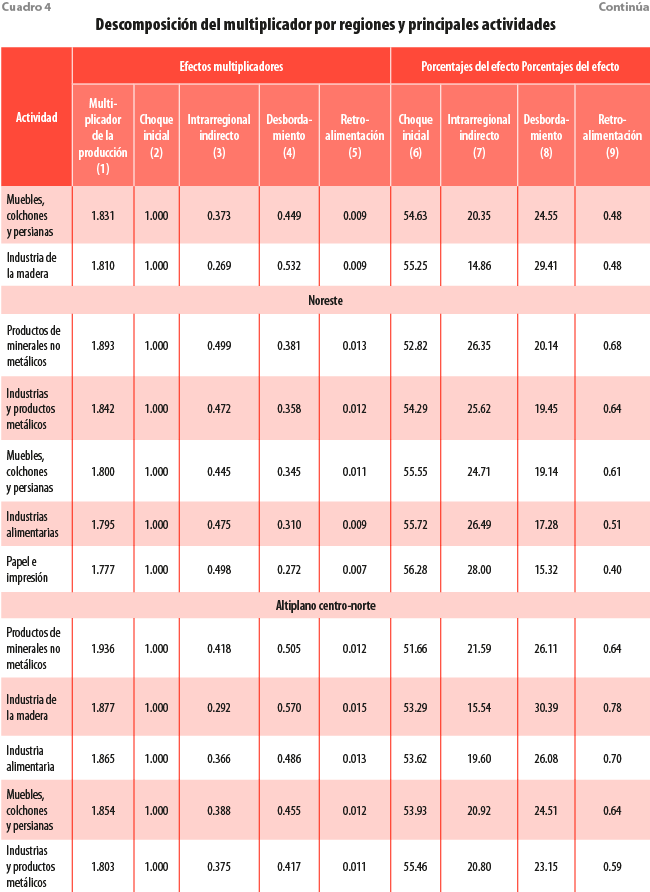
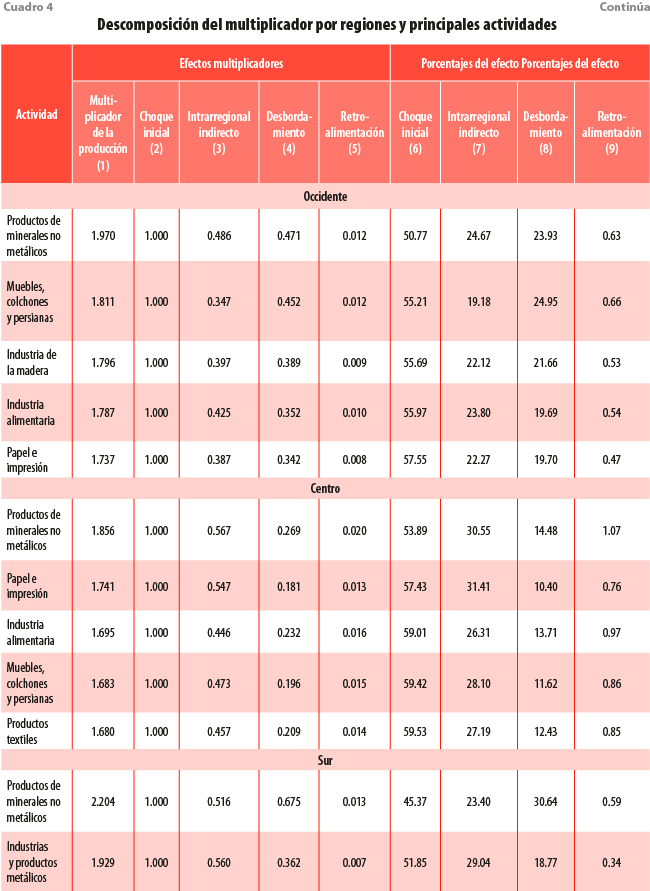
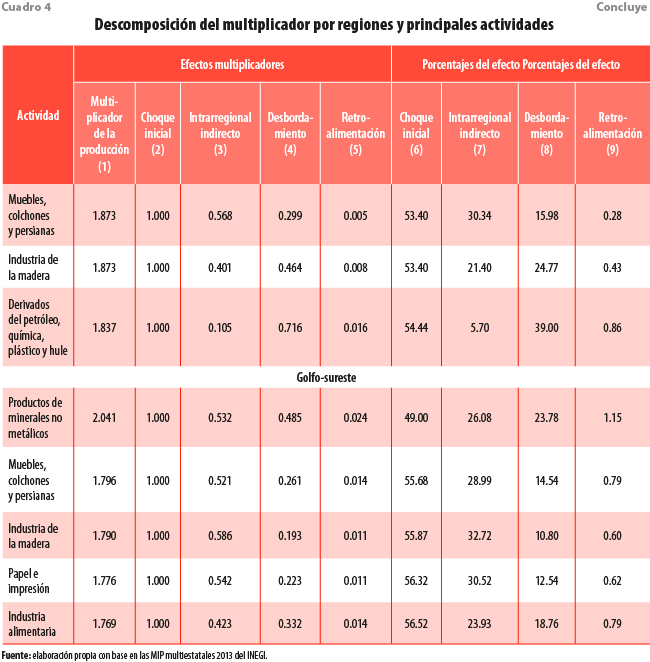
Para simplificar la exposición de los resultados, en el cuadro 4 solo se reportan las cinco actividades con los multiplicadores más altos de cada región. Contemplan los efectos multiplicadores directos del choque inicial, los intrarregionales indirectos y los interregionales por desbordamiento y retroalimentación. 

Sobresale que la actividad Productos de minerales no metálicos presenta el multiplicador más alto en las siete regiones, aunque tiene el mayor en la sur y el más bajo en la centro. En general, su efecto multiplicador tiende a estar más orientado a la parte intrarregional, con excepción de las regiones altiplano centro-norte y la sur, donde el impacto interregional es más alto. También, se destaca la región golfo-sureste, donde el efecto de retroalimentación resultó más grande con 1.15 % del impacto total.

Destacamos que, en ninguna región, los servicios se encuentran entre las actividades que tienen efectos multiplicadores más altos. También, sobresale la ausencia de la Industria productora de maquinaria y equipo, es decir, la manufactura más intensiva.

Las industrias con los multiplicadores más altos tienden a ser las mismas en todas las regiones pues, aunque sus técnicas de producción sean marginalmente distintas en cada región, así como presentar requerimientos de importaciones distintos, la esencia de cómo se producen los bienes es relativamente homogénea en todos los estados. Esto se refuerza con la poca dispersión observada en los valores de los multiplicadores de la mayoría de las actividades mostradas en la gráfica.

En este sentido, destacamos el caso de la región sur, la cual es la única donde la actividad Industria alimentaria no alcanzó los primeros cinco lugares en términos del multiplicador, y fue reemplazada por la de Derivados del petróleo, química, plástico y hule. Esta también sobresale por tener un alto porcentaje (39) de efectos de desbordamiento, es decir, muchos de los insumos requeridos en su cadena de producción se demandan a otras regiones del país.

 

Conclusiones

El análisis de la descomposición estructural del aparato productivo fue posible gracias a la disponibilidad de matrices insumo-producto multiestatales para el 2013, interconectadas mediante los flujos de comercio interregional, recientemente publicadas por el INEGI. Esta fuente de información permite tener un conjunto de matrices estatales comparables y con flujos contablemente consistentes tanto a nivel intra como interestatal para las 32 entidades federativas.

En este trabajo se propone una generalización del método de descomposición estructural multiplicativa, aplicable a MIP con más de dos regiones, que es consistente con las interpretaciones de Pyatt y Round (1979) y con la aditiva de Stone (1985). Gracias a esta descomposición, es posible obtener por primera vez no solo el valor de los efectos de desbordamiento, sino también saber hacia cuál región específica se dan estos. La obtención de resultados generados por este método podría extenderse para considerar las 32 entidades federativas de México en un solo modelo.

Entre los resultados de los efectos interregionales, se destaca que la región centro es la que absorbe los principales efectos de desbordamiento de todas las demás, gracias a su concentración de actividades de servicios, mientras que los de retroalimentación fueron muy poco significativos para todas las regiones, lo que refleja la casi nula circularidad de los impactos cuando salen de la región de origen.

De acuerdo con la hipótesis de trabajo, es posible apreciar que los efectos multiplicadores de carácter interregional son significativos en el efecto multiplicador total, representando 14 % en promedio. Se muestra que la centro y noreste son las economías con una menor dependencia de insumos del resto del país, mientras que la sur aparece como el caso contrario; los casos de la altiplano centro-norte, occidente, noroeste y golfo-sureste muestran estructuras más balanceadas entre su capacidad interna y sus interdependencias interregionales. Esto comprueba que las regiones menos desarrolladas tienen efectos de desbordamiento interregional más altos.

Finalmente, el estudio de la descomposición estructural que ha empleado las MIP multiestatales del 2013 constituye un esfuerzo poco abordado desde la perspectiva metodológica, analítica y de aplicación práctica, además de que representa una aportación a las herramientas para el diagnóstico, formulación y aplicación de políticas económicas en el ámbito del desarrollo regional mexicano.

______________

Fuentes

Albornoz, L., J. Becerril y R. Ortiz. “Los efectos económicos del COVID-19 en México. Un enfoque de insumo-producto”, en: Ciencias Administrativas Teoría y Praxis. 2(17), 2021, pp. 67-84 (DE) bit.ly/3RgAIhU

Alvarado, J., M. Quiroga, L. Torre y D. Chiquiar. “Matrices insumo-producto regionales y una aplicación para analizar las exportaciones manufactureras en México”, en: Ensayos: Revista de Economía. 38(2), 2019, pp. 227-258 (DE) bit.ly/47t7Atw

Amaral, E., I. Fernandes, M. Ibarrarán, R. Boyd, A. Elizondo y J. Belausteguigoita. “Modelo interestatal de insumo-producto para México, 2013”, en: Revista Análisis Económico. 35(90), 2020, pp. 7-43 (DE) bit.ly/49TB8lN.

Asuad, Normand. “Metodología y resultados de la construcción de matrices estatales insumo producto de abajo hacia arriba mediante la elaboración de cuadros de oferta y utilización estatales”, en: Realidad, Datos y Espacio Revista Internacional de Estadística y Geografía. 11(2), 2020, pp. 74-89.

Chiquiar, D., J. Alvarado, M. Quiroga y L. Torre. Regional input-output matrices, an application to manufacturing exports in Mexico. Documentos de investigación. Banco de México, 2017 (DE) bit.ly/3T1T0Fc.

Chapa, J. “Impacto económico del COVID-19 en las regiones de México”, en: Revista Ciencia UANL. 23(102), 2020, pp. 18-23 (DE) bit.ly/3uGXBCg.

Chapa, J. y E. Ayala. El súbito freno de la economía a causa del COVID-19. Un ejercicio sobre su posible impacto. Publicación especial del Centro de Investigaciones Económicas. 2020 (DE) https://bit.ly/48k5egB.

Dávila, A. (coord.). Modelos interregionales de insumo producto de la economía mexicana. México, Universidad de Coahuila-Miguel Ángel Porrúa, 2015, 318 pp.

Dávila, A. y M. Valdés. “México. Costos económicos del cierre de las actividades ‘no esenciales’ por la pandemia COVID-19. Análisis multisectorial y regional con modelos SAM”, en: Economía, Teoría y Práctica. Número especial, 2020, pp. 15-45 (DE) doi:10.24275/ETYPUAM/NE/E052020/Davila.

Defourny, J. y E. Thorbecke. “Structural path analysis and multiplier decomposition within a social accounting matrix framework”, en: The Economic Journal. 94(373), 1984, pp. 111-136.

Fuentes, N., A. Brugués y G. González. “Simulación de un modelo insumo-producto dinámico: multiplicadores de producción para Coahuila”, en: Revista de Economía UADY. 35(91), 2018, pp. 93-117.  

Hewings, G. J. D. Regional Input-Output Analysis. 1985. Reprint 2020. Edited by Grant Ian Thrall. WVU Research Repository  (DE) bit.ly/47Sl2XL.

Gaytán, E. y J. Vargas. “Agrupamientos industriales de la economía del estado de Hidalgo, México: un enfoque de insumo producto”, en: Economía, Sociedad y Territorio. 19(60), 2019, pp. 47-78.

INEGI. Cuadros de oferta y utilización y matrices insumo-producto multiestatales: fuentes y metodología. Documento de investigación. México, INEGI, 2022, pp. 1-48.

Isard, W. “Interregional and regional input-output analysis: a model of space economy”, en: Review of Economics and Statistics. 33(4), 1951, pp. 318-328.

Miller, R. y P. Blair. Input-output analysis: foundations and extensions. 3rd edition. New York, Cambridge University Press, 2022.

Pyatt, G. y J. Round. “Accounting and fixed price multipliers in a social accounting matrix structure”, en: Economic Journal. 89, 1979, pp. 850-873.

Round, J. I. “Decomposing multipliers for economic systems involving regional and world trade”, en: The Economic Journal. 95(378), 1985, pp. 383-399.

Stone, R. “The Disagreggation of the household sector in the national account”, en: Paytt, G. y J. Round (eds.). Social accounting matrices: a basis for planning. Washington D. C., World Bamk, 1985, pp. 145-185.

Torre, L., J. Alvarado y M. Quiroga. Matrices insumo-producto regionales, una aplicación al sector automotriz en México. Documentos de investigación. Banco de México, 2017 (DE) bit.ly/3R2mlfZ.

^[1] Esta sección se limita a describir de manera somera y sucinta el documento metodológico sobre la construcción de la MIP multiestatal de México. Para una descripción más detallada de los procesos, consultar el documento metodológico del INEGI (2022).

^[2] Programa estadístico del INEGI con datos referidos al 2013.