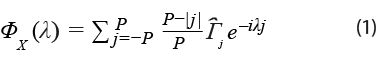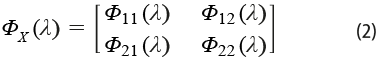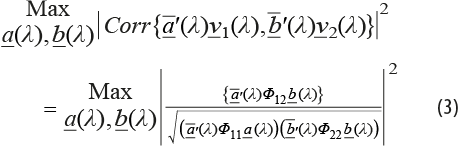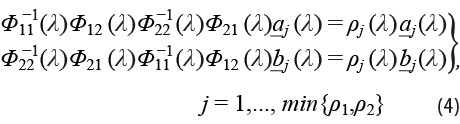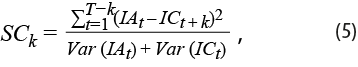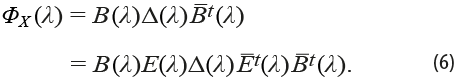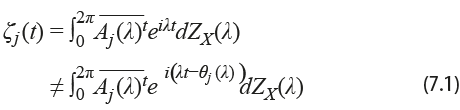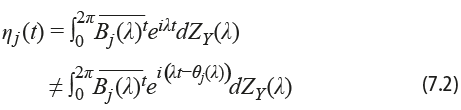Desarrollo de ponderadores óptimos para indicadores cíclicos basado en el análisis multivariado espectral de series de tiempo

 

Development of Optimal Weights for Cyclical Indicators Based on
Multivariate Spectral Time-Series Analysis

 

Víctor Alfredo Bustos y de la Tijera y Noemí López Delgado*
* Instituto Nacional de Estadística y Geografía (INEGI), alfredo.bustos@inegi.org.mx y nohemi.delgado@inegi.org.mx, respectivamente.

 

Vol. 13, Núm. 1 Epub                                             Desarrollo de ponderadores...  Epub

En este trabajo revisamos un método propuesto por Bustos (1993) para desarrollar conjuntos de ponderadores óptimos para el desarrollo de indicadores cíclicos también óptimos. Para ello, recurrimos al análisis canónico de series de tiempo multivariadas en el dominio de las frecuencias siguiendo a Brillinger (1981). Para llevar a cabo comparaciones útiles, utilizamos los conjuntos de indicadores coincidentes y adelantados, en uso por el Sistema de Indicadores Cíclicos del Instituto Nacional de Estadística y Geografía (SIC-INEGI), para el periodo enero del 2004 a marzo del 2020. La primera aplicación del procedimiento sugerido al conjunto de datos no resulta en un comportamiento óptimo. Mostraremos, sin embargo, como nuestra propuesta permite evaluar los indicadores candidatos a entrar en el análisis, lo que resultará en conjuntos refinados. A partir del resultado de este proceso de selección, se realiza una nueva aplicación de la metodología. Con base en criterios tales como la correlación cruzada a distintos rezagos o por la capacidad de hacer pronósticos del indicador coincidente a partir del adelantado, evaluamos la ganancia a la que conduce nuestra propuesta. Los resultados obtenidos de esta manera superan en más de un sentido el comportamiento de indicadores desarrollados mediante métodos tradicionales. Palabras clave: indicadores compuestos; cíclicos; coincidente; adelantado; función de correlación cruzada; series multivariadas de tiempo; análisis espectral; dominio de las frecuencias; correlación canónica; pronósticos.

In this paper we review a method proposed by Bustos (1993) to develop sets of optimal weights for the development of cyclical indicators that are also optimal. For this purpose, we resort to the canonical analysis of multivariate time series in the frequency domain, following Brillinger (1981). To carry out useful comparisons, we use the sets of coincident and leading indicators, in use by the Cyclical Indicators System of the National Institute of Statistics and Geography (SIC-INEGI), for the period January 2004 to March 2020. The first application of the suggested procedure to the data set does not result in optimal behaviour. We will show, however, how our proposal allows evaluating the candidate indicators to enter the analysis, which will result in refined sets. Based on the result of this selection process, a new application of the methodology is carried out. Based on criteria such as the cross-correlation to different lags or by the ability to make forecasts of the coincident indicator from the leading one, we evaluate the gains to which our proposal leads. Results obtained in this way outperform in more than one sense the behaviour of indicators developed using traditional methods. Key words: composite indicators; cyclical; coincident; leading; cross-correlation function; multivariate time series; spectral analysis; frequency domain; canonical correlation; forecasts.

Recibido : 28 de enero de 2021.
Aceptado: 1 de junio de 2021.

 

Introducción

El ser humano ha desarrollado ingeniosos esquemas para anticipar el futuro. Entre estos se encuentran los sistemas de indicadores compuestos coincidentes (ICC) y adelantados (ICA), cuyo fin es determinar de forma oportuna las variaciones inherentes al comportamiento cíclico de una economía. A pesar de haber surgido hace ya casi un siglo, su metodología básica ha experimentado solamente cambios menores. Aunque no parece haberse explicitado de esta manera, a nuestro juicio, el principal propósito de los sistemas de indicadores cíclicos (SIC) es el de obtener pronósticos precisos de valores futuros del indicador compuesto coincidente a partir de la información disponible hoy en día para el cálculo del ICA. Las metodologías actualmente en uso para la elaboración de los SIC tienen su origen en el trabajo pionero de los señores Mitchell^[1] y Burns^[2], del Buró Nacional de Investigación Económica (NBER, por sus siglas en inglés) de los Estados Unidos de América (EE. UU.), durante el primer tercio del siglo XX. Además de su discípulo Geoffrey Moore,^[3] diversos organismos nacionales e internacionales han seguido sus pasos y realizado aportaciones que tienen el propósito de mejorar los resultados. A partir de 1995, y a la fecha, The Conference Board (ver TCB, 2001) ha continuado publicando resultados periódicos (ver TCB, 2020) tanto para los EE. UU. como para otros países. Sin embargo, los aspectos fundamentales de la propuesta original permanecen en todas ellas.

En efecto, permanece el reconocimiento de la incapacidad de un único indicador para proveer un adecuado resumen del comportamiento cíclico reciente de la economía de un país. Es por ello que, en todos los casos, se busca identificar un conjunto de indicadores, denominados coincidentes, cuya agregación se espera que cumpla mejor el papel de aproximar el mencionado comportamiento. En general, dicha identificación se lleva a cabo fechando los cambios de dirección en la evolución de cada indicador y comparando el fechado con el de un indicador de referencia que recoge el comportamiento agregado de la producción en los sectores productivos, el Producto Interno Bruto (PIB) o, preferentemente, algún indicador mensual de la actividad industrial. Cuando los cambios de dirección en las crestas o en los valles coinciden con gran frecuencia, se considera estar frente a un indicador coincidente. De manera similar se llega a la identificación de un segundo conjunto de indicadores, denominados adelantados, cuyas crestas y valles ocurren en el tiempo, por lo general, antes que las del indicador de referencia.

La información contenida en cada uno de los conjuntos desarrollados como se ha descrito, o la de su crecimiento, se resume mediante la suma ponderada de los valores contemporáneos de los distintos indicadores para obtener los agregados. Con el paso del tiempo, los sistemas de ponderación han venido simplificándose. Originalmente, el fechado de crestas y valles, así como la determinación de los conjuntos de coeficientes, tenían lugar mediante reuniones de expertos durante las cuales se buscaba lograr acuerdos sobre sus valores. Al parecer, la ausencia de un criterio de optimalidad que indicara para qué se hacía lo que se hacía, y la consecuente dificultad para comparar entre propuestas y resultados, llevó a abandonar esta práctica. Hoy en día, aun sin un criterio tal, parece existir un acuerdo que indica que las mencionadas ponderaciones sean basadas en la variabilidad de cada uno de los indicadores con el fin de evitar otorgar un peso mayor a aquellas que muestran mayor inestabilidad durante el periodo de observación.

Una adición reciente a la metodología consiste en el uso de versiones de los indicadores cuya tendencia secular ha sido reducida o, de plano, eliminada. Para este fin, se ha recurrido a propuestas tales como el filtro de Hodrick y Prescott (Hodrick et al., 1997) o, como en el caso de la Organización para la Cooperación y el Desarrollo Económicos (OCDE, 2012), a consideraciones del análisis espectral de series de tiempo; en este caso, se procede reduciendo la potencia para una o más de las frecuencias más pequeñas mediante un filtro.

La experiencia en la aplicación de metodologías como la que hemos resumido en párrafos anteriores es, más bien, mixta. Ya que uno de sus propósitos más importantes es el de anticipar caídas indeseables en el desempeño económico con el fin de actuar con oportunidad para mitigar sus efectos negativos sobre las personas y las empresas, parecería sensato elegir de entre todas las opciones disponibles aquella que conduzca a un menor error de pronóstico. En el pasado reciente, esto hubiera sido de gran importancia frente a una crisis como la que se desató hacia finales del 2008 y cuyos efectos residuales son perceptibles aún hoy en día. Si juzgamos por la magnitud de lo ocurrido entonces, parecería que los pronósticos obtenidos no dieron cuenta de ella, o que quienes toman decisiones de política económica los ignoraron. En el caso mexicano, el INEGI determinó cambiar la metodología que había seguido hasta antes del 2009 (ver INEGI, 2015) a partir de esa experiencia (ver Yabuta, 2010).

Es posible encontrar en la literatura intentos que buscan la incorporación de herramientas más modernas del análisis econométrico de series de tiempo en la elaboración de indicadores coincidentes y adelantados. Por ejemplo, Stock et al. (1989) buscan dar respuesta a tres preguntas básicas; desde una perspectiva conceptual, se cuestionan si es posible desarrollar un modelo probabilístico formal que dé lugar a ICC y a ICA, y permita su evaluación; asimismo, se preguntan sobre el mejor conjunto de variables a ser incluidas en el ICA y, finalmente, indagan acerca de la mejor forma de combinar dichas variables para producir índices útiles y confiables. Su metodología se compone de dos etapas, y parte de la identificación de un conjunto de variables coincidentes a partir de las cuales se obtiene un solo factor dinámico, común a todas ellas, que será utilizado a manera de indicador coincidente. Acto seguido, y bajo la consideración de un conjunto amplio de condiciones de identificabilidad, modelan como una autorregresión vectorial al vector estocástico formado por el factor dinámico y las variables adelantadas, poniendo particular atención en la ecuación para este. Exhiben ejemplos de la aplicación de su propuesta haciendo uso de la información disponible para la construcción de los indicadores coincidentes y adelantados elaborados por el NBER.

Nos ocuparemos de las que consideramos son las limitaciones más importantes de las metodologías actualmente en uso a lo largo del resto de la presente sección. Llama la atención que las que nacieron hace casi un siglo no hayan incorporado los desarrollos teóricos y metodológicos del análisis estadístico de series multivariadas de tiempo que han sido publicados desde entonces, ni el apreciable fortalecimiento de las tecnologías de información disponibles hoy en día. Puede ser que con propósitos normativos se requiera del fechado de crestas y valles con el fin de llevar a la administración pública a actuar para paliar las consecuencias de una caída, o a dejar de hacerlo cuando ya no se requiera. Sin embargo, prácticas razonables del análisis de series de tiempo sugerirían aprovechar favorablemente, además, la información que se presenta entre unas y otros a través de los patrones de autocorrelación y de correlación cruzada. Una consecuencia de proceder de esta manera sería que el fechado de los puntos de giro, tal vez la única posibilidad de relacionar dos indicadores tomando en cuenta las metodologías de cálculo disponibles a principios del siglo XX, perdería relevancia en un contexto actual.

Tampoco puede soslayarse la ausencia de un criterio de optimalidad que permita establecer mejores valores para los coeficientes de los indicadores. Hoy en día parecen determinarse los de un conjunto sin tomar en consideración la información contenida en el otro. El mencionado propósito de obtener un pronóstico indirecto (para distinguirlo de autoproyecciones) con precisión razonable parece tampoco tener relevancia para este fin.

Seguramente, cuando el objetivo es contrastar los valores de un indicador en un momento con los que presenta en otro, se hace necesario restringir la agregación de valores solo a los contemporáneos; por ejemplo, esa es la costumbre para los índices de Laspeyres o de Paasche. Cabe preguntarse si cuando el propósito es diferente, como ha quedado establecido, es razonable o deseable mantener la restricción a valores contemporáneos. La popularización de los modelos ARIMA (Box y Jenkins, 1970), para el caso univariado, o las autorregresiones vectoriales^[4] (VAR, por sus siglas en inglés), para el multivariado, se debe a que mejoran la precisión de los pronósticos a través de la consideración de rezagos diferentes de cero.

La propuesta resumida en Bustos (1993) ya ofrecía respuestas a varias de las anteriores inquietudes y limitaciones. Su principal fuente de inspiración es Brillinger (1980, Ch. 10), específicamente su tratamiento del análisis canónico de series de tiempo, aprovechando la perspectiva del dominio de las frecuencias. El razonamiento básico detrás de la propuesta era que, cuando se estudia el ciclo de negocios o el económico, resulta natural aproximar las series de tiempo que lo representan mediante sumas ponderadas de funciones periódicas con coeficientes estocásticos, en un rango de frecuencias, es decir, sus transformadas de Fourier. Algunas aplicaciones recientes de este enfoque al análisis econométrico pueden ser encontradas en Pollock (2014a, 2014b y 2018).

Son diversas las ventajas de proceder de esta manera. En primer lugar, se tiene que este enfoque no da lugar a pérdidas de información; simplemente, corresponde a un análisis complementario de esta desde una perspectiva diferente. Además, en el caso estacionario se tiene que los segundos momentos se simplifican. En particular, lo anterior concede la posibilidad de trasladar algunas técnicas multivariadas del análisis estadístico de vectores aleatorios, aplicándolas frecuencia a frecuencia. De forma similar, la tendencia secular común a todas las series puede ser removida mediante la reducción de la potencia en las frecuencias bajas del espectro de la primera componente principal, obtenido a partir de la totalidad de las series bajo consideración. Versiones estacionarias de los indicadores originales se obtienen a partir del conjunto de componentes principales modificado.

Otra consecuencia de lo anterior es que, contra la costumbre, se introducen criterios explícitos para evaluar la calidad del resultado; por ejemplo, el análisis canónico busca determinar vectores de coeficientes que maximizan el cuadrado de la norma de las coherencias en cada frecuencia. Cabe esperar que, al regresar al dominio del tiempo, los resultados también exhiban correlaciones cruzadas óptimas para uno o más rezagos. Es de esperarse, en consecuencia, que los pronósticos aportados por el ICA para el ICC resulten ser óptimos en algún sentido.

Otra limitación que aquella propuesta buscaba estudiar se refiere al supuesto, no siempre corroborado, de que un único indicador compuesto para cada conjunto resume toda la información relacionada con el ciclo, contenida en los datos originales. Es así como, al dar lugar a más de un conjunto de parejas, el enfoque sugerido permite apreciar la reducción óptima de las dimensiones.

El resto de este trabajo procede de la siguiente manera. En la sección que continúa se elabora un breve esbozo de la metodología propuesta, así como de algunos resultados relevantes. Procederemos entonces a aplicar nuestra propuesta a la información utilizada en la construcción del SIC-INEGI. De este modo, podremos llevar a cabo una comparación entre ambos conjuntos de resultados, introduciendo para este fin los criterios que consideramos adecuados. Enseguida, y aprovechando estos, propondremos una estrategia para eliminar indicadores indeseables del conjunto de los coincidentes. Algo semejante ocurrirá con el de los adelantados. Finalmente, con el resultado del anterior proceso de selección, se realizará una nueva aplicación de nuestra metodología y su resultado será comparado con el del procedimiento actualmente en uso por el INEGI. Concluiremos con un breve resumen de nuestros resultados y con la discusión de algunos planteamientos para investigación futura que permitan aprovechar cabalmente la información disponible.

Análisis canónico de series multivariadas de tiempo

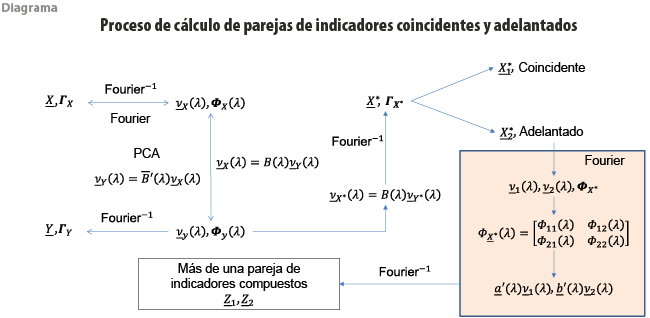
Como se mencionó, el principal propósito de los SIC es el de obtener pronósticos precisos de valores del indicador compuesto coincidente k > 1 periodos en el futuro a partir de información actualmente disponible para el cálculo del ICA. A partir de este planteamiento se sigue naturalmente la idea de utilizar el análisis canónico de series multivariadas de tiempo. Un bosquejo de la propuesta para el cálculo de un SIC se encuentra en el diagrama 1. En él pueden identificarse dos partes para llevar a cabo el análisis. En primer lugar, partiendo de la información original del conjunto de n series , así como de estimadores de sus segundos momentos , se realiza el análisis por componentes principales (PCA, por sus siglas en inglés) en el dominio de las frecuencias, usando sus transformadas de Fourier. Enseguida, a partir de la información derivada del análisis anterior o de la misma información original, tiene lugar el análisis canónico propiamente dicho, también en el dominio de las frecuencias.

En todos los casos se encuentran sus versiones equivalentes en el dominio de las frecuencias, el vector  y la matriz Φ_x(λ); en esencia, sus transformadas de Fourier, finitas y discretas. Para cada una de las frecuencias λ_j=2πj ⁄ T, j=0, … ,T-1, partiendo de la diagonalización de la matriz espectral Hermitiana Φ_x(λ_j), se realiza el mencionado análisis de componentes principales. En otras palabras, mediante la matriz B, cuyas columnas son los vectores característicos de la matriz espectral, se obtiene un nuevo conjunto de coeficientes de Fourier, cuya matriz espectral resulta ser diagonal. A través de la transformada inversa de Fourier se tiene un nuevo conjunto de series , así como su estructura de covarianza , la cual está formada, aproximadamente, por matrices diagonales. Se consigue de esta manera que este conjunto tenga correlaciones cruzadas nulas, a semejanza de lo que ocurre en el análisis de componentes principales de vectores aleatorios independientes.

En el diagrama, la anterior secuencia se encuentra dentro del cuadrado definido por las flechas bidireccionales, las cuales son así ya que, como se indica en el exterior de dicho cuadro, es posible recorrer la secuencia en sentido contrario para pasar de  a  nuevamente. Ello permite, además, producir diferentes versiones de las series originales a través de la manipulación del conjunto de componentes principales; por ejemplo, de la modificación de algunas y/o de la eliminación de otras. En otras palabras, pasar de   a  donde posiblemente tendencias o influencias estacionales han sido removidas del conjunto de series  para dar lugar al de , así sea solo para las primeras componentes principales. En efecto, ya que PCA tiene lugar frecuencia a frecuencia, podemos decidir cómo reducir el contenido de frecuencia en la parte baja del espectro para, por ejemplo, la primera componente principal, lo que, en general, dará lugar a nuevas versiones o proxies de las series originales, cuyas tendencias serán apenas perceptibles. Este tratamiento recuerda al descrito en OCDE (2012, Anexo A), con la diferencia de que, en su caso, la eliminación de las frecuencias bajas tiene lugar serie a serie.

El nuevo conjunto de indicadores dará lugar, a su vez, a por lo menos dos subconjuntos de series. En primera instancia se tendrá al conjunto de coincidentes integrado por series cuyo comportamiento cíclico es semejante en más de un sentido al de un indicador de referencia; por ejemplo, la mensual de producción industrial. Por otro lado, se tendrá al conjunto de series adelantadas cuyo comportamiento cíclico antecede al de la de referencia. En este caso, con el fin de hacer un uso eficiente de toda la información disponible, la determinación de los conjuntos de series coincidentes o adelantados tiene lugar atendiendo al comportamiento de las estructuras de correlación cruzada de todos y cada uno de los candidatos con un indicador de referencia. En breve, lo que esto significa es que ni los puntos de giro en crestas y valles ni su fechado forman parte relevante de nuestro enfoque.

 

Una vez determinados los tamaños de cada subconjunto, denotados por p₁ y p₂, se estima la matriz espectral del vector, cuyas primeras p₁ componentes están formadas por las series coincidentes; las restantes p₂ las ocupan las adelantadas. La estimación se lleva a cabo como se indica en (1):

 

                              

 

Dicha matriz es particionada conformablemente en bloques, según las dimensiones p₁ y p₂, como se indica en la expresión (2):

 

     

 

Con base en ella, y para cada una de las frecuencias λ_j, se plantean los problemas de optimización indicados en (3), de cuyas soluciones se obtendrán los vectores de coeficientes a(λ_j), b(λ_j)  que conducen a los pares canónicos espectrales (ver Brillinger, 1981, Teorema 10.3.2), en directa generalización del caso en el que se está en presencia de vectores independientes (ver, por ejemplo, Morrison, 1967, Cap. 6):

 

 

Se tiene que a(λ) y b(λ) maximizan el cuadrado de la norma de la coherencia dentro del par canónico. Observamos que es posible obtener nuevas parejas de vectores al imponer condiciones de nula correlación entre diferentes pares canónicos para resolver problemas de optimización similares a (3). Lo anterior puede llevarse a cabo hasta un número de veces igual al menor de los valores p₁ y p₂. Más aún, bajo la condición de identificabilidad de que los vectores de coeficientes obtenidos de esta manera tengan una norma igual a 1, se tiene que dichos vectores son, a su vez, soluciones no nulas a los sistemas de ecuaciones presentados en (4). En otras palabras, a(λ) y b(λ)  son vectores característicos de las matrices que aparecen en la expresión (4). Rescribiéndolos como   y , y haciendo uso de la desigualdad de Schwartz puede probarse que el máximo valor característico coincide con el óptimo del criterio (3):

 

 

A partir de cada una de estas soluciones, se definen nuevos conjuntos de coeficientes de Fourier. Nuevamente, la transformada inversa de Fourier de estos resultados dará lugar a nuevas series de indicadores cuya correlación cruzada, se espera, resultará máxima para algún rezago. Se forma un nuevo vector de series , en cuyas primeras p₁ componentes se concentran los indicadores coincidentes y en los subsecuentes p₂, los adelantados. Por construcción, el cálculo de los indicadores resultantes puede contemplar, además de los valores contemporáneos, los rezagados de las series originales. De este modo, dejan de tener vigencia las restricciones implícitas en el cálculo de índices, que suponen que los valores de los coeficientes para dichos rezagos son iguales a cero. Por ello, cabe pensar que el criterio de optimalidad alcanzará mejores niveles.

Para el caso de los ejemplos numéricos que se presentan a continuación, obtenidos del sitio de INEGI,^[5] las tendencias, así como la estacionalidad, han sido removidas. Más aún, todas las series han sido también suavizadas y clasificadas como coincidentes o adelantadas. Consecuentemente, nuestra discusión se centra en la parte metodológica enmarcada en la esquina inferior derecha del diagrama.

 

Ejemplo de aplicación de la metodología y comparación de sus resultados con los del SIC-INEGI

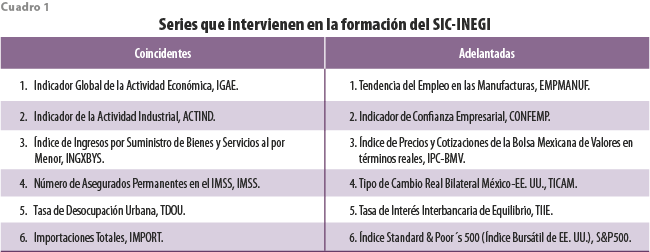
Como se mencionó, usamos indicadores cuya tendencia ha sido removida con el fin de que la comparación se centre solo en la determinación de las ponderaciones que llevan a los indicadores agregados. En el cuadro 1 se enlistan, junto con sus mnemónicos, las series que forman parte de cada uno de los conjuntos coincidente y adelantado, seleccionadas de acuerdo con lo que se indica en INEGI (2015). Según esta publicación, a los indicadores originales se les removió una tendencia y se les suavizó mediante la doble aplicación del filtro de Hodrick y Prescott. Tampoco es aparente patrón estacional alguno. El periodo contemplado cubre 195 observaciones, a partir de enero del 2004 y hasta marzo del 2020.

 

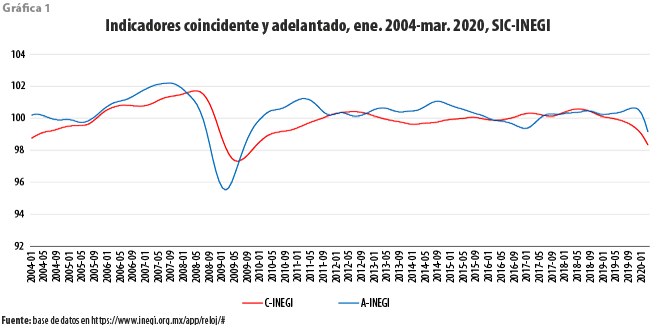
Por principio de cuentas, se comentan primeramente los resultados obtenidos por el INEGI mediante su propuesta metodológica (ver INEGI, 2015). En la gráfica 1 se muestra la única pareja resultado de agregar las series que forman cada uno de los conjuntos en el cuadro 1, según dicha metodología. Como puede observarse, el ICA tiene un comportamiento deseable en cuanto a crestas y valles hacia el principio del periodo; sin embargo, hacia el final de este, parece perder la mencionada cualidad. Parece claro que, en tanto el ICC ha venido descendiendo por espacio de casi dos años, aquel indicador presenta un ligero incremento durante el inicio de ese lapso, y solo para los meses más recientes exhibe una tendencia negativa.

 

 

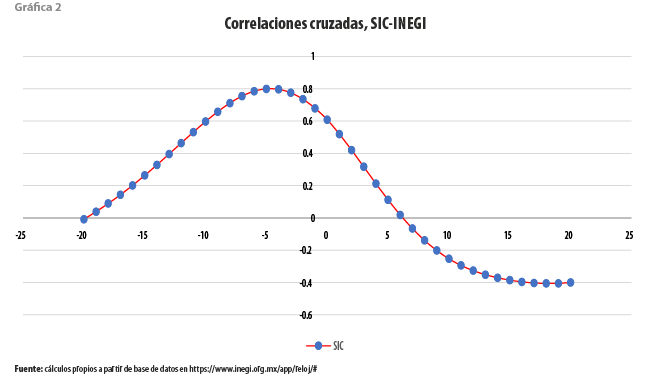
A pesar de lo anterior, según se muestra en la gráfica 2, la estructura de correlación cruzada entre ambos indicadores muestra que el adelanto entre uno y otro es, en promedio, de alrededor de cinco meses a lo largo de todo el periodo contemplado. El valor de la correlación cruzada a ese rezago es igual a 0.7921, siendo significativamente diferente de cero cualquiera que sea el criterio de prueba. Este valor representa la cota contra la cual habremos de medir el desempeño de alternativas.

 

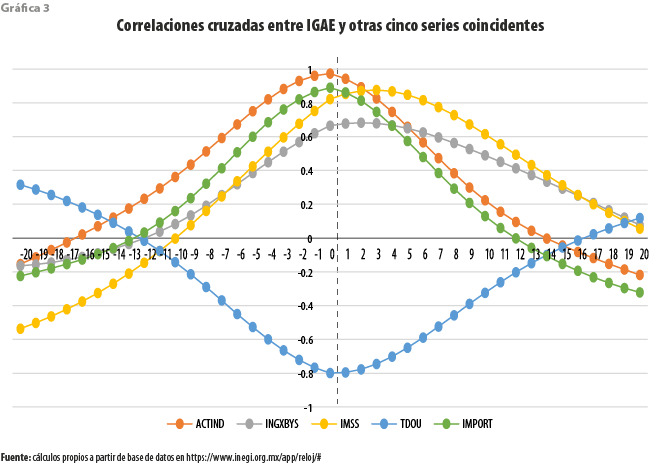
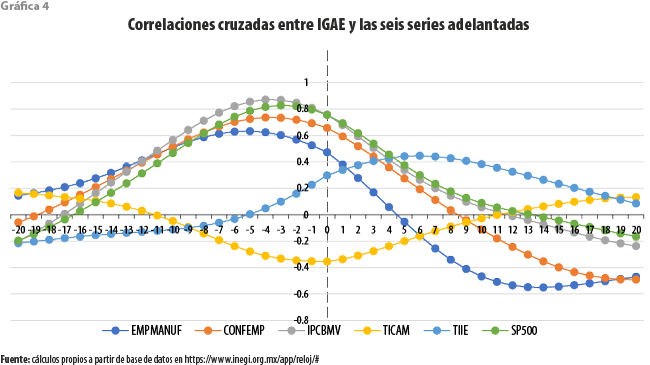
Como ya fue señalado, y con el fin de aprovechar de manera eficiente la información disponible, para nuestra propuesta resulta más relevante la consideración de los patrones de correlación cruzada entre las series consideradas. Por ello, en las gráficas 3 y 4 se resumen estos para, por un lado, el IGAE, como serie de referencia, y por el otro, cada una de las series restantes.

A partir de la primera de ellas se vuelve aparente que tanto las series de actividad industrial como de importaciones, así como la Tasa de Desocupación Urbana son, en promedio, series en efecto coincidentes. No es igualmente claro que lo sean las que se refieren al registro de asegurados en el Instituto Mexicano del Seguro Social (IMSS), y a los ingresos por suministro de bienes y servicios. La primera de ellas muestra una correlación máxima con el IGAE de 0.8579 a un rezago de tres meses, en tanto que la segunda presenta una relación más débil de alrededor de 0.68 a rezagos de uno, dos y tres meses.

Algo similar ocurre con el conjunto de series adelantadas, entre las cuales cuatro de ellas (EMPMANUF, IPC-BMV, CONFEMP y S&P500) aportan evidencia de un comportamiento adelantado con respecto al IGAE, con correlaciones máximas desde poco más de 0.6 hasta casi 0.9. Entre las restantes, el TICAM daría la impresión de ser un indicador coincidente, aunque con una correlación contemporánea débil; la TIIE tiene una apariencia de ser rezagado con respecto al de referencia, mostrando también una débil correlación de casi 0.45 a un rezago de seis meses.

 

 

 

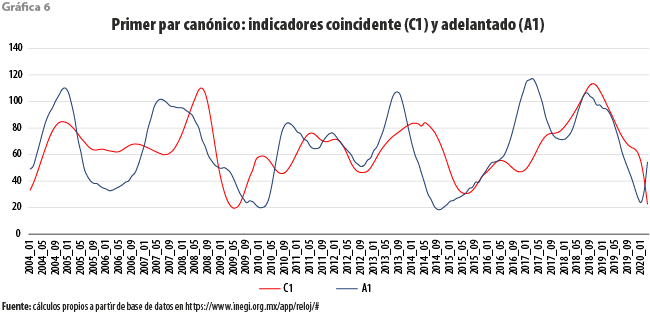
Una parte del resultado de aplicar nuestra propuesta se ilustra en las gráficas 6 y 7, donde se muestran, respectivamente, el primer y segundo pares canónicos. En el primer caso, por principio de cuentas, no parece quedar clara la relación entre indicador coincidente con la serie de referencia. Asimismo, tampoco es del todo claro que el adelantado, en efecto, adelante al coincidente, ni por cuantos meses.

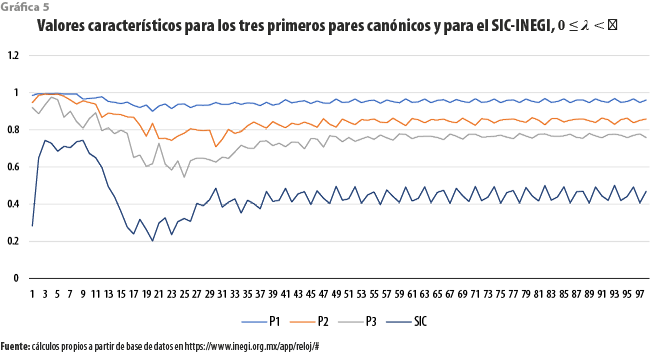
Por su parte, la gráfica 5 muestra los valores propios para cada una de las frecuencias armónicas 0 ≤ λ < π, para tres de los seis pares de series canónicas que es posible obtener, así como el que corresponde, cuando se aplica la metodología descrita, a los indicadores univariados coincidente y adelantado del SIC-INEGI. Es claro que el primer par canónico es óptimo, en términos del criterio establecido, sobre cualesquiera filtros lineales calculados a partir de las series coincidentes y adelantadas, incluidos los considerados en este trabajo. Debe ser claro, sin embargo, que algunos de los pares canónicos restantes también contienen información útil y, por construcción, casi ortogonal a la aportada por el primer par; es decir, en el estudio del ciclo no es necesario restringirse a una única pareja de indicadores.

Una parte del resultado de aplicar nuestra propuesta se ilustra en las gráficas 6 y 7, donde se muestran, respectivamente, el primer y segundo pares canónicos. En el primer caso, por principio de cuentas, no parece quedar clara la relación entre indicador coincidente con la serie de referencia. Asimismo, tampoco es del todo claro que el adelantado, en efecto, adelante al coincidente, ni por cuantos meses.

 

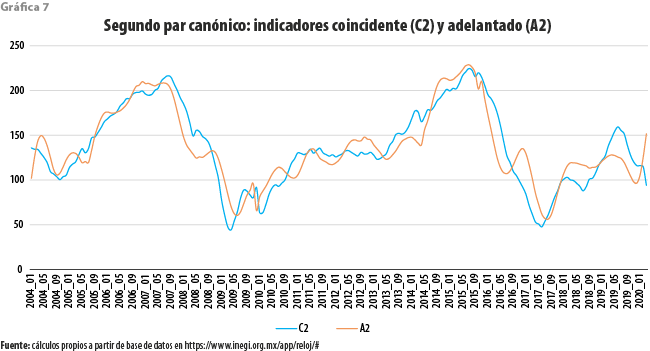
Por lo que toca al segundo par canónico, de manera contraintuitiva se obtiene una pareja de indicadores que muestran una relación más estrecha. El ICA adelanta a su pareja al inicio de los periodos de recuperación, pero lo opuesto ocurre al de los de decremento. Cabe señalar que el comportamiento cíclico exhibido por esta pareja parece tener referencia a un ciclo de más largo plazo con una duración aproximada de cinco años, que solo puede ser aproximadamente establecida ante lo corto del periodo de observación.

 

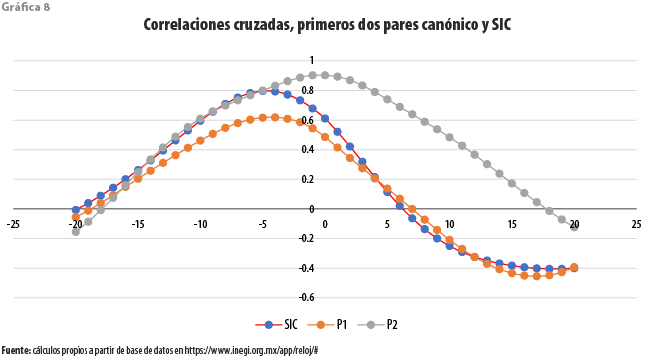
Las estructuras de correlaciones cruzadas que se muestran en la gráfica 8 parecen ratificar las consideraciones hechas anteriormente en relación con los dos primeros pares canónicos. En efecto, el patrón para la primera pareja, denotado por P1, indica un débil adelanto contra el que sería de esperarse; el indicador adelantado parece adelantar al coincidente, con una correlación de 0.62 a entre cuatro y cinco meses. Por lo que toca al correspondiente al segundo par canónico, tenemos ahora una situación más clara. Su correlación máxima a rezago cero, que parece confirmar la alternancia en adelantos descrita, alcanza el valor de 0.902, mayor que la exhibida por la pareja del SIC. Es evidente que la optimalidad del criterio en el dominio de las frecuencias no se traduce siempre en resultados óptimos en el dominio del tiempo.

 

 

 

Complementación de la propuesta

Los anteriores e insatisfactorios resultados nos han llevado a plantear algunas hipótesis, las cuales esperamos nos conduzcan a situaciones más favorables. La primera de ellas se refiere al cumplimiento de diversos supuestos, en particular, al que tiene que ver con los datos. De manera muy simple, es posible resumirla como “las series coincidentes coinciden con el indicador de referencia, y las adelantadas, lo adelantan”. Las gráficas 1 y 2 nos dicen que, en términos de los segundos momentos que son centrales al procedimiento, no todas las series seleccionadas parecen satisfacer dicho supuesto. Lo anterior nos obliga a echar una mirada más cuidadosa a nuestros insumos. Además de su relación con la serie de referencia, nos interesa saber cuál es la que guardan las coincidentes con las adelantadas. Para este fin, proponemos aplicar el procedimiento sugerido al caso en el que el conjunto de series coincidentes está formado por una sola de ellas a la vez; el de las adelantadas puede contener a las seis originales o a algún subconjunto de ellas. Al primer caso, lo denotaremos por 1X6.

Este ejercicio recuerda al denominado Indicador Oportuno de la Actividad Económica (IOAE), dado a conocer recientemente por el INEGI. En este ejercicio se recurre a modelos empíricos de nowcasting para estimar tanto la variación porcentual anual como los niveles del IGAE y de dos grandes actividades económicas. El modelo utiliza^[6] “… un amplio conjunto de indicadores oportunos y de alta frecuencia, por ejemplo: variables obtenidas de encuestas económicas, series de tiempo financieras, indicadores extraídos de fuentes no tradicionales, entre otros…”. En estricto sentido, el indicador no pronostica al IGAE, sino es una estimación para este obtenida a partir de información cuya publicación tiene lugar de manera más oportuna y corresponde al mismo mes para el que se estima el valor del IGAE (i. e., k = 0), que será difundido con posterioridad.

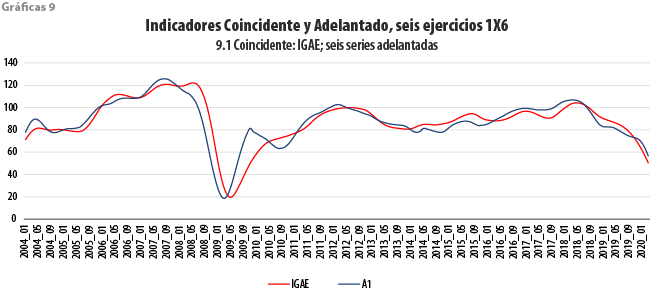
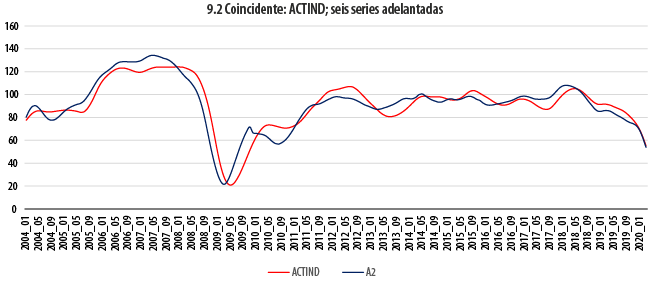
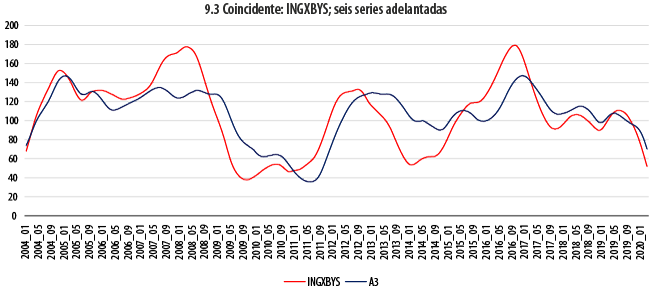
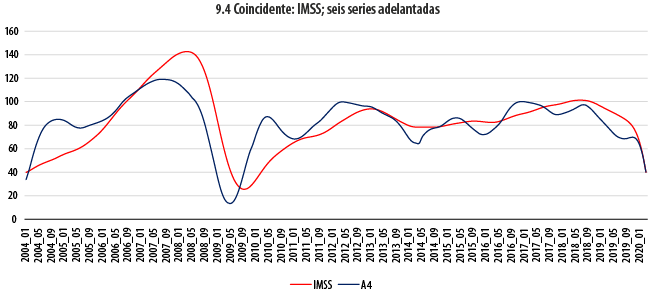
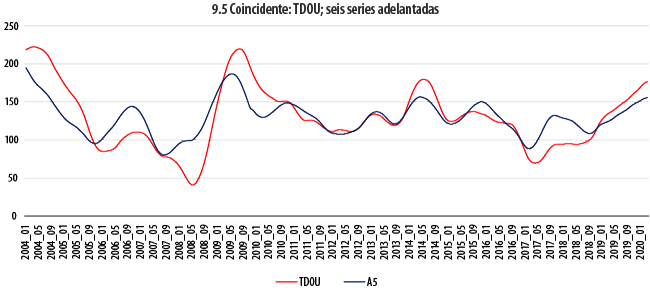
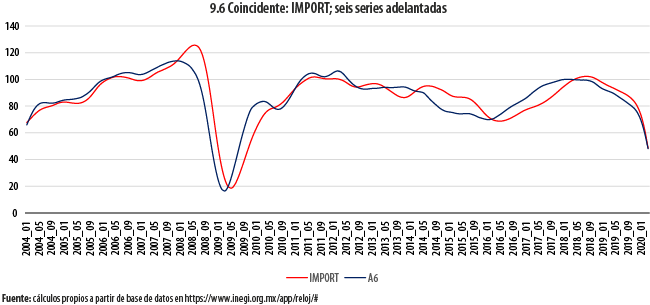
Las gráficas 9 dan cuenta de la comparación a lo largo del tiempo de la evolución de las series coincidentes con combinaciones de las seis adelantadas. En cada uno de los seis paneles que componen dichas gráficas, la serie coincidente, cuyo comportamiento se busca adelantar, aparece en color rojo, en tanto que su correspondiente indicador adelantado se muestra en azul. Antes de recurrir a otras estadísticas para evaluar el resultado de estos ajustes, ya es aparente, a simple vista, que para las tres series coincidentes (IGAE, ACTIND e IMPORT) se obtiene un indicador adelantado con las características deseables; las tendencias se siguen de manera cercana, pero mostrando un adelanto, en particular en las crestas y los valles, de al menos un par de meses, en general. De forma similar, las dos series que de una u otra manera tienen que ver con la ocupación (IMSS, TDOU) no exhiben un comportamiento igualmente afortunado. Aun cuando versiones suavizadas de estas dos series y de sus correspondientes indicadores adelantados exhibirían similitudes importantes, las oscilaciones que algunas de ellas presentan hacen pensar en la dificultad de obtener buenos pronósticos de una a partir de la otra. En el otro extremo se encuentra el caso de la serie INGXBYS, para la cual el indicador adelantado parece ir, de hecho, rezagado.

 

 

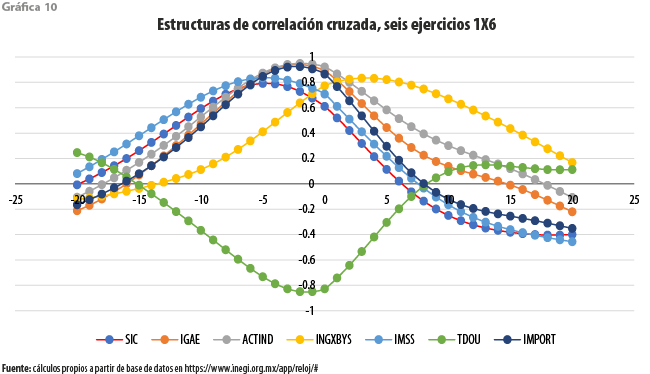
En la gráfica 10 se resumen todas las estructuras de correlación cruzada para cada uno de los anteriores ejercicios; para fines de comparación, se incluye también a la de SIC-INEGI. En ella encontramos evidencia que ratifica algunos de nuestros hallazgos anteriores. Para las series IGAE, ACTIND e IMPORT, se tiene que las tres parejas formadas muestran una correlación máxima superior a 0.9 para un rezago de dos meses. Tanto para estas como para la denominada IMSS, las correlaciones máximas son superiores en magnitud a nuestro benchmark, el SIC-INEGI, cuya correlación máxima a un rezago de cinco meses no rebasa el valor de 0.8. Para esta cuarta serie, la máxima correlación con su indicador adelantado ocurre para un rezago de cinco meses; en otras palabras, y contra lo que pudiera pensarse a partir de su autocorrelación con el IGAE, dicho indicador adelantado podría aportar una predicción con un adelanto de cinco meses, en promedio. Es, de hecho, la serie para la cual se tiene el mayor adelanto. En el caso de la serie TDOU, en cambio, se tiene que el adelanto más correlacionado ocurre a un rezago de solamente un mes, con un valor de -0.85, que sigue siendo mejor que el mencionado benchmark. Finalmente, se ratifica que la serie INGXBYS marcha adelante del indicador adelantado que busca aproximarla.

 

 

Ahora bien, si entendemos el propósito general de nuestro ejercicio como el de obtener buenas aproximaciones para valores futuros de una o más series a partir de los valores presentes y rezagados de otras, vale la pena introducir un criterio que nos permita determinar el éxito o no con el que se alcanza este propósito, el cual, por supuesto, debe tomar en cuenta las sumas de cuadrados de los errores de aproximación que resultan para cada modelo y rezago. Sin embargo, ya que las escalas con las que se presentan los resultados del SIC son diferentes de las de los obtenidos de la aplicación de nuestra propuesta, decidimos estandarizar las mencionadas sumas de cuadrados dividiéndolas entre la suma de las varianzas de cada serie:

    

donde IA_t es el indicador adelantado e IC_t, el coincidente.

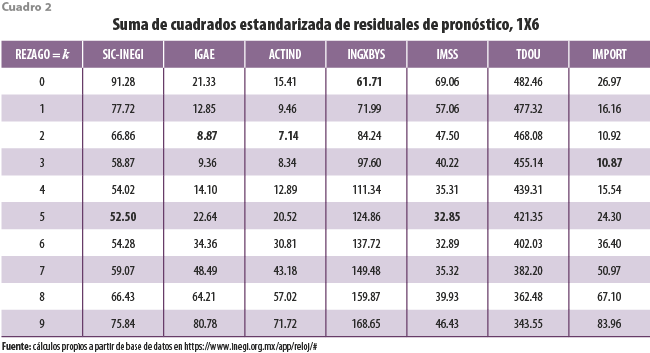
El cuadro 2 resume los valores del anterior criterio, tanto para el SIC-INEGI como para cada uno de los 1X6 ejercicios anteriormente mencionados, para cada uno de los primeros 10 rezagos. En su primera columna muestra lo que ocurre con el SIC-INEGI, alcanzando su valor mínimo para un rezago de cinco meses; cabe destacar que dicho valor se encuentra por arriba de 50. Por lo que toca a las series coincidentes, entre todas ellas destaca el pobre desempeño del pronóstico que busca aproximar valores futuros para la serie TDOU, lo que la ubica en una clase aparte; los del criterio incluidos presentan una tendencia a decrecer, pero para los rezagos mostrados no es perceptible que se alcance un valor mínimo. Tampoco observa un comportamiento deseable el pronóstico para la serie INGXBYS que, como se recordará, parece adelantar a su indicador adelantado; tal vez por ello muestran una tendencia decreciente hacia valores negativos del rezago. De manera consistente con los patrones de correlación cruzada mostrados en la gráfica 10, el menor valor del criterio se ubica a un rezago de cinco meses. Ahora, contra lo que ocurre para el caso del SIC-INEGI, dicho valor ya se encuentra por debajo de 50. De esta forma llegamos a identificar las tres series con mejores valores para el error de pronóstico: IGAE, ACTIND e IMPORT. Para las dos primeras, los óptimos se dan a un rezago de dos meses, en tanto que para la tercera ocurre casi un empate para los rezagos a dos y tres meses. Vale la pena destacar, sin embargo, que los valores del criterio a rezago cinco meses se encuentran todos por debajo de 50 para estas series y para la del IMSS.

 

 

 

 

 

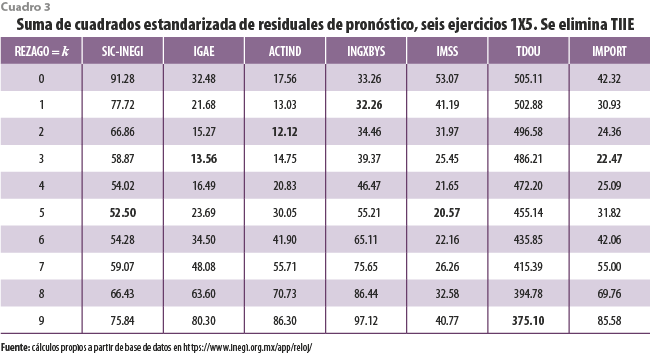
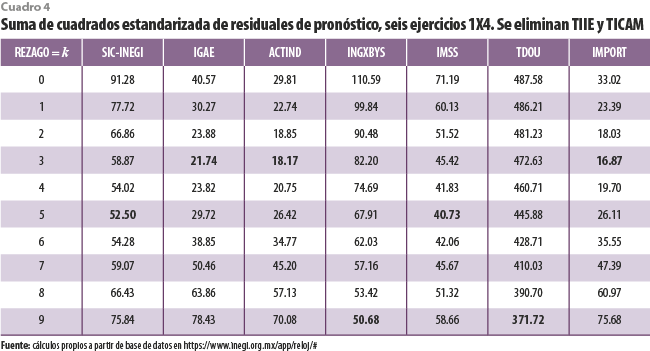
A partir de la discusión anterior, las series coincidentes INGXBYS y TDOU son candidatas para salir del análisis, por lo menos cuando el indicador adelantado considera a las seis así identificadas. Se llega a conclusiones semejantes cuando se excluyen en sucesión, de entre las adelantadas, a la TIIE y al TICAM (cuadros 3 y 4, respectivamente). A partir de ellas conviene señalar que los valores del criterio relacionado con residuales de pronóstico parecen crecer a medida que el tamaño del conjunto de series adelantadas se reduce.

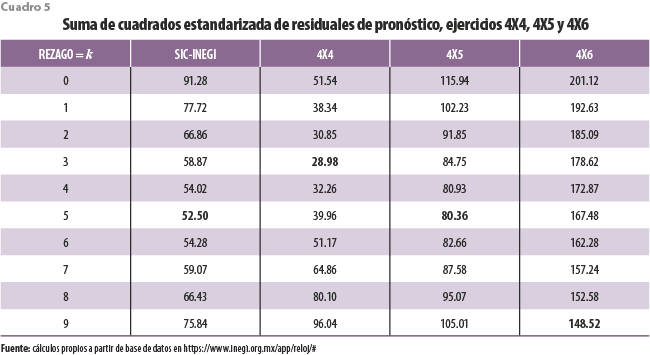
A pesar de lo anterior, para los ejercicios que simultáneamente contemplan a las mencionadas cuatro series coincidentes, los residuales de pronóstico tienden a ser menores en magnitud a medida que el número de las adelantadas se reduce. El cuadro 5 da cuenta de este comportamiento.

 

Propuesta para el sistema de indicadores compuestos, coincidentes y adelantados

A partir de los resultados discutidos en la sección anterior, concluimos que los mejores se obtienen cuando se eligen dos conjuntos de series, cada uno consistente en cuatro de ellas. El ejercicio 4X4 que presentaremos enseguida contempla a IGAE, ACTIND, IMSS, e IMPORT como el conjunto de las coincidentes; por su parte, entre las adelantadas se incluye a EMPMANUF, CONFEMP, IPCBMV y SP500.

 

 

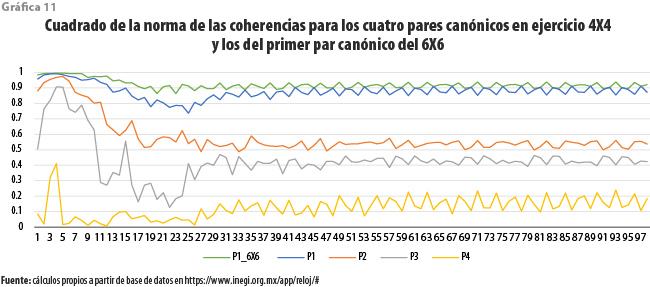
Observamos a partir de la gráfica 11 que la eliminación de información da lugar a un decremento ligero en los valores del cuadrado de la norma de las coherencias para la primera pareja canónica en distintas frecuencias. En otras palabras, en términos de este criterio, los resultados que se presentan serían considerados subóptimos. La pérdida es más notoria para un conjunto de ciclos con una duración de entre siete y 20 meses, aproximadamente. En general, las restantes parejas canónicas muestran valores alejados del comportamiento óptimo; es decir, para este ejemplo es poco probable que contribuyan de manera importante al estudio del comportamiento cíclico de la economía.

 

 

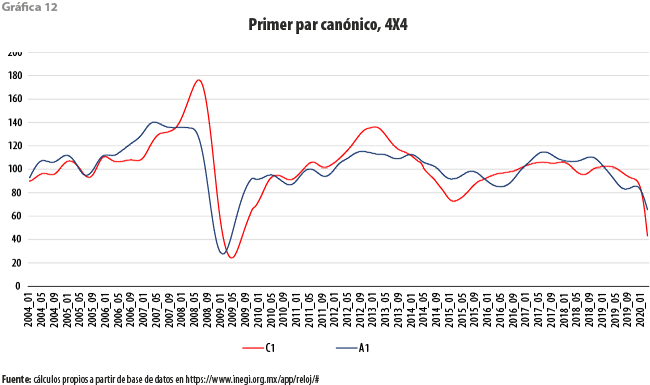
La evolución conjunta de ICC e ICA, es decir, de los elementos del primer par canónico, se muestra en la gráfica 12. Como podrá observarse, la relación que guardan ambos es cercana a lo que se espera de ellos. Por supuesto, destaca su comportamiento deseable entre el 2008 y 2009. Hacia el final del periodo, los dos exhiben una tendencia decreciente que se inicia en octubre del 2018, para el ICA, en tanto que el ICC comienza su caída entre diciembre de ese año y enero del siguiente.

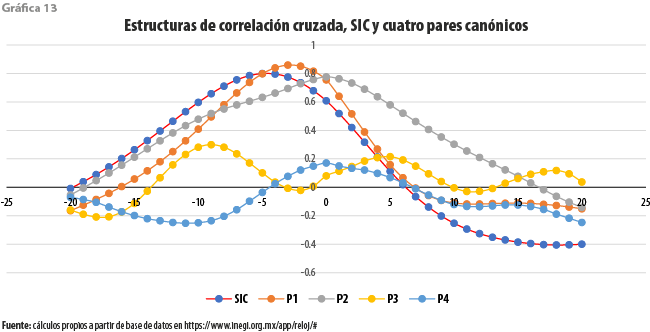
Las estructuras de correlación para las cuatro parejas canónicas obtenidas en este ejercicio, así como para el SIC-INEGI, incluido con fines de comparación, se recogen en la gráfica 13. La débil relación lineal entre los elementos de los pares canónicos segundo, tercero y cuarto es puesta de manifiesto en dicha gráfica. Esta vez, sin embargo, la asociación entre los elementos de la primera pareja alcanza un valor máximo cercano a 0.85 para un rezago de tres meses, el cual resulta superior a los exhibidos por el SIC-INEGI a lo largo de los rezagos incluidos, todos ellos inferiores a 0.8.

 

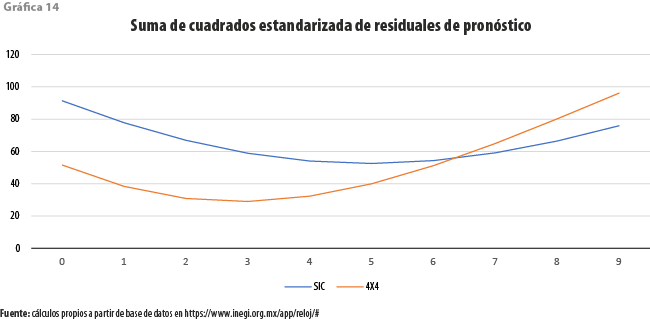
Por lo que toca al criterio referente a la capacidad de pronóstico del indicador adelantado en relación con el coincidente, se tiene también que el nuevo sistema de indicadores es superior al SIC-INEGI, con un adelanto óptimo de tres meses. Solo, en la medida en la que nos alejamos de los respectivos óptimos, queda claro que nuestra propuesta no es uniformemente mejor.

 

La optimalidad en el dominio de las frecuencias no se traduce automáticamente en correlaciones cruzadas óptimas

Cuando discutimos las limitaciones del procedimiento propuesto, mostradas en el ejercicio 6X6, hicimos referencia a más de una hipótesis que las explicara. Hasta ahora, nos hemos concentrado en los datos y sus limitaciones. Sin embargo, conocemos una segunda causa para la cual, sin embargo, no tenemos aún una respuesta adecuada. Nuestra propuesta procede resolviendo un problema de optimización, frecuencia a frecuencia. Como ya hemos indicado, la optimización correspondiente para cada frecuencia no parece conducir necesariamente a comportamientos óptimos en el agregado representado por las inversas de Fourier. Esta vez, la sospecha recae en los mismos vectores propios que son solución a cada problema de optimización.

Los vectores propios son únicos, salvo por su multiplicación por un complejo de norma uno. Es fácil ver que, para la matriz Hermitiana Φ_x(λ), se debe tener que, en vista de la conmutatividad del producto de matrices diagonales, las igualdades en (6) son satisfechas. En ellas, las columnas de la matriz B(λ) son sus vectores característicos, la matriz diagonal Δ(λ) está formada por los valores característicos correspondientes y E(λ) es una matriz diagonal arbitraria, cuyos elementos no nulos tienen la forma  e^{iθ_j (λ)}:

 

 

Dicha expresión da lugar a representaciones espectrales equivalentes para la matriz Φ_x(λ). Sin embargo, cuando dichos vectores característicos reciben un uso diferente, como en el caso que nos ocupa, los resultados pueden no ser tan favorables. No queda claro que el par de series canónicas  ζ_j (t) y η_j (t), definidas en (7.1) y en (7.2), resulten ser invariantes cuando las fases para cada frecuencia pueden ser modificadas a capricho:

 
   

 

En nuestro intento por traducir las rutinas al lenguaje R, hemos encontrado que los resultados pueden ser muy diferentes, tal vez por la misma razón. Los resultados discutidos con anterioridad fueron obtenidos haciendo uso de la rutina DEVCHF, parte de la librería IMSL, originalmente escrita en Fortran, la cual resulta en vectores ortonormales y, aparentemente, impone la restricción de que la entrada con mayor norma del eigenvector sea forzada a tomar un valor real. En el caso de R, hemos recurrido a la función EIGEN, la cual, en adición a la condición de ortonormalidad, fuerza a la primera de las entradas de cada vector a ser un número real. En ambos casos, la operación es equivalente a multiplicar al vector por un complejo sobre la circunferencia unitaria. Esta parece ser la razón principal para la diferencia entre los resultados.

Comentarios finales y conclusiones

Hemos mostrado una aplicación del procedimiento descrito por Brillinger al problema de desarrollar ponderadores óptimos para un sistema de indicadores cíclicos. A partir de nuestra discusión, queda claro que la optimalidad en el dominio de las frecuencias no se hereda de manera directa al del tiempo. Hemos descrito, también, cómo aprovechar la misma metodología para realizar una selección, de entre un grupo de indicadores candidatos, de los que pasarán a formar parte de la propuesta final. A pesar de lo anterior, arribamos a indicadores compuestos que se comparan favorablemente con las propuestas en operación hoy en día, con base en un conjunto de criterios deseables. En consecuencia, el procedimiento debe ser reemplazado, por lo pronto, por soluciones subóptimas, hasta en tanto se encuentren las condiciones que conduzcan desde la solución óptima en el dominio de las frecuencias, a la mejor en el del tiempo. Dichas condiciones habrán de reflejarse en propuestas de modificación de los resultados de diversas rutinas para el cálculo numérico de valores y vectores característicos. Nos encontramos explorando algunas alternativas prometedoras que esperamos poder reportar pronto.

El camino seguido para alcanzar los resultados presentados ilustra una forma para realizar una selección de los candidatos a integrar cada conjunto. En efecto, aun cuando las crestas y los valles mostrados por una serie anticipen o coincidan con los de la de referencia, parece útil considerar otros aspectos, como los aquí discutidos antes de tomar una decisión. Por otro lado, en condiciones de alta volatilidad de los indicadores, parece necesario revisar la exclusión de algunas series o la inclusión de otras más.

Nuestra presentación se ha concentrado en aspectos econométricos y estadísticos de los sistemas de indicadores cíclicos. Ignoramos cuáles serían los resultados del SIC si en este momento se hiciera una selección semejante de los datos de entrada. Parece haber conciencia de que algunos de los indicadores considerados por este sistema han perdido, en el pasado reciente, su carácter de coincidentes o adelantados. Sin embargo, no se han tomado acciones para eliminarlos o reemplazarlos por otros. Ello no parece deberse a la deseabilidad de mantener la comparabilidad tanto en el tiempo como con otros países. En el primer caso, la eliminación de la tendencia mediante el uso del filtro de Hodrick-Prescott conduce a modificaciones de los valores de los indicadores aun en el pasado remoto, mes a mes; es decir, se actúa como si la comparabilidad a lo largo del tiempo se sigue dando a pesar de los mencionados cambios, pues se aplica el mismo procedimiento durante todo el periodo de observación, y ello nos parece razonable. En el segundo, se tiene que la selección de los indicadores básicos se realiza de manera independiente en cada país, por lo que tampoco parece preocupar la comparabilidad.

 

___________

Fuentes

 

Box, G. E. P. y Jenkins, W. Time Series Analysis: Forecasting and Control. San Francisco, Holden-Day, 1970.

Burns, A. F. y Mitchell, W. Measuring Business Cycles. National Bureau of Economic Research. Studies in business cycles, First Edition. 1964 (DE) consultado el 11 de noviembre de 2020 en: https://bit.ly/3iQ0FCQ

Bustos, A. “Statistical Methodology for Leading Indicator Systems”, en: Bulletin of the International Statistical Institute. Contributed Papers, Book I. 49th session. Florence, Italy, 1993, pp. 189-190.

Brillinger, D. R. Time Series, Data Analysis and Theory. San Francisco, Holden Day, Inc., 1981.

The Conference Board, Business Cycle Indicators Handbook, The Conference Board, 2001. Consultado el 11 de Nov., 2020 en https://bit.ly/3Ls5caT

_______ U.S. Business Cycle Indicators. THE CONFERENCE BOARD LEADING ECONOMIC INDEX (LEI) FOR THE UNITED STATES AND RELATED COMPOSITE ECONOMIC INDEXES FOR SEPTEMBER. 2020 (DE) en: https://bit.ly/3LldHEM

Hannan, E. J. Multiple Time Series. New York, John Wiley & Sons, Inc., 1970.

Hodrick, R. J. and E. C. Prescott. “Postwar U.S. Business Cycles: An Empirical Investigation”, en: Journal of Money, Credit and Banking. Vol. 29, No. 1, Feb. Blackwell Publishing, 1997, pp. 1-16.

INEGI. Metodología para la construcción del sistema de indicadores cíclicos, Instituto Nacional de Estadística y Geografía. 2.ª ed. México, INEGI, 2015 (DE) consultado el 11 de noviembre de 2020 en: https://bit.ly/3DjQiAR

Lahiri, K. and Moore, G., (1993), Leading Economic Indicators, Cambridge University Press.

Mitchell, W. and Burns, A. F., "Statistical indicators of cyclical revivals", en: Bulletin 39. New York, NBER, 1938 (DE) consultado el 11 de noviembre de 2020 en: https://bit.ly/3tMzWxl

Morrison, D. F. Multivarate Statistical Methods. New York, McGraw-Hill Inc., 1967.

OCDE. OECD System of Composite Leading Indicators. Paris, OECD, 2012 (DE) consultado el 11 de noviembre de 2020 en: https://bit.ly/36TC6Cs

Pollock, D. S. G. Trends, Cycles and Seasons: Econometric Methods of Signal Extraction. Working Paper No. 14/04, February. UK, University of Leicester, 2014a.

_______ Econometric Filters. Working Paper No. 14/07. UK, University of Leicester, 2014b.

_______ “Filters, Waves and Spectra”, en: Econometrics. 6, 35, 2018 (DE) consultado el 11 de noviembre de 2020 en: https://bit.ly/3ILcd4Z

Stock, J. H. y M. W. Watson. “New Indexes of Coincident and Leading Economic Indicators”, en: Blanchard and Fischer (eds.). NBER Macroeconomics Annual. Volume 4. MIT Press, 1989.

Yabuta, Y. New tools for tracking the Mexican Business Cycle, ESA/STAT/AC. 223/S3.5. Third International Seminar on Early Warning and Business Cycle Indicators, 17-19 November 2010, Moscow, Russian Federation, 2010 (DE) Consultado el 11 de noviembre de 2020 en: https://bit.ly/3LlUbIn

^[1] https://bit.ly/3tQ9ROg

^[2] https://bit.ly/3qJYTHS 

^[3] https://bit.ly/36xGc3x

^[4] Es frecuente encontrar el uso del término vectores autorregresivos en referencia a estos modelos. Tal denominación es resultado de una traducción deficiente del inglés Vector Auto-Regression.

^[5] Disponibles en: https://bit.ly/3uyZuxn

^[6] https://bit.ly/3DkM63E