En años recientes, el estudio matemático de redes complejas que modelan problemas del mundo real ha tenido importantes avances. En este artículo consideramos gráficas que representan diversos sistemas de transportación a nivel nacional y al de ciudad. Las técnicas de la teoría de gráficas y el análisis matricial permiten definir medidas de centralidad que determinan, a partir de la topología de la gráfica, la importancia relativa de los vértices; información que, en muchos casos, es estratégica en la solución de problemas. Nuestra atención se concentrará en dos medidas de centralidad: la que se da por cercanía y la espectral. Como aportación original de este trabajo al estudio de la complejidad de las redes de transporte introducimos el concepto de coherencia de una red, medida que indica qué tanto la estructura de la red de transporte está construida de acuerdo con los requerimientos reales. Nuestros análisis de redes usan datos auténticos de los sistemas mexicanos de transportación. Palabras clave: red de transporte, gráfica pesada, distancia, medida de centralidad, valor propio, coherencia.		We consider graphs as models of different sorts of transportation networks, both at national level: highways and plane routes, and at city level: subway and bus systems. Graph theory techniques and matrix analysis consider centrality functions which define a ranking, depending only on the topological structure, among the vertices of the graph. These functions provide strategic information for the resolution of various problems. Closeness centrality is used in the study of the efficiency of the transportation networks. Spectral centrality (the local values of an eigenvector associated to the spectral radius) is used in the study of the coherence of the transportation networks. We introduce the concept of coherence as a measure of how a transportation network structure meets the needs of users. We use real data of the mexican transportation systems and draw conclusions on their performance. Key words: transportation network, weighted graph, distance, centrality measure, eigenvalue, coherence.

 

Nota: este trabajo fue realizado durante una visita en agosto del 2012 del EMALCA (acrónimo de la Escuela Matemática de América Latina y el Caribe) Team al Centro de Investigación en Matemáticas (CIMAT) en Guanajuato, México; los miembros del grupo agradecen su hospitalidad y apoyo financiero.

 

1. Sistemas de georreferenciación

Durante los siglos XV al XVII, la cartografía tuvo desarrollos importantes gracias a las observaciones de los navegantes y al uso de nuevas técnicas de medición, como: la brújula, el telescopio y el sextante. Para 1492, Martin Behaim (cartógrafo alemán) construía el primer globo terráqueo, el Erdapfel, lo cual requería de la determinación de las coordenadas de lugares sobre la Tierra. La latitud (basada en el Ecuador celeste) era conocida desde la más remota antigüedad, pero la longitud (que no es un parámetro relacionado con la Astronomía sino con mediciones en la superficie terrestre) fue mucho más difícil de establecer.

En 1714, el Parlamento británico designó el Comité de la Longitud y solicitó la cooperación de hombres de ciencia, entre los que se encontraban Isaac Newton y Edmund Halley. El problema principal (resuelto por John Harrison) radicaba en la creación de cronómetros exactos resistentes a las inclemencias climáticas. Desde ese momento, todas las naves de investigación cartográfica llevaron a bordo varios de éstos, de cuya exactitud dan fe las cartas náuticas de la época.

El siguiente paso fue el establecimiento de un meridiano de referencia a partir del cual se pudiera calcular de forma precisa el tiempo en cada parte del planeta. De acuerdo con la arbitrariedad de la posible elección, se optó por la línea que cruzaba las islas Canarias, de manera que el primer meridiano fue el que pasó por Orchilla, en la isla de El Hierro, que aún hoy es conocida como la isla del meridiano. Después, hubo otras propuestas hasta que en 1911, la línea que atraviesa el Old Royal Observatory de Greenwich pasó a ser la referencia mundial para calcular la hora universal.

En la cartografía, la tecnología ha cambiado continuamente para resolver las demandas de nuevas generaciones de fabricantes de mapas y de lectores de los mismos. Las primeras cartas fueron elaboradas de forma manual con plumas sobre pergaminos; hoy en día, disponemos de complejos sistemas de posicionamiento, como el Global Positioning System (GPS) y satélites con relojes nucleares que son capaces de determinar, con una exactitud sin precedentes la posición de cualquier persona que cuente con un teléfono celular u otro dispositivo de bolsillo.

Estos sistemas de georreferenciación o geolocalización, así como las bases de datos asociadas a los de información geográfica (SIG), tienen importantes aplicaciones en la toma de decisiones estratégicas; por ejemplo, si se combinan eficazmente los datos de un censo con mapas virtuales es posible determinar dónde existe una mayor densidad poblacional y, así, tomar decisiones en relación con la construcción de escuelas, hospitales y otros inmuebles. En tiempo real, la geolocalización sirve también a los servicios de emergencia que pueden detectar rutas rápidas para llegar a determinados lugares, vías de escape o los mejores puntos de acceso ante cualquier eventualidad en la que resulte esencial la rapidez; en el área del transporte público, permite saber por dónde van los autobuses y cuánto tiempo tardarán en llegar a cierto punto específico.

El crecimiento de las capacidades informáticas a nivel global hace posible no sólo el conocimiento e intercambio de grandes cantidades de datos, sino el análisis de ellos por medio de programas de índole estadístico y matemático. En años recientes, el estudio matemático de redes complejas que modelan problemas del mundo real ha tenido importantes avances: por una parte, la teoría espectral de gráficas, que descubre valiosa información de la estructura topológica de las redes, codificada en los valores y vectores propios de matrices asociadas a las redes, y por la otra, el estudio de la evolución temporal de las redes que motivó la introducción del concepto redes libres de escala, las cuales han sido identificadas como las que se forman en la interacción de las sociedades humanas.

En este artículo consideramos gráficas que representan diversos sistemas de transportación a nivel nacional (carreteras y líneas aéreas) y de ciudad (Metro y líneas de autobuses). Las técnicas de la teoría de gráficas permiten definir medidas de centralidad que determinan la importancia relativa de cada vértice en la gráfica. El interés de éstas es que proveen información adicional a la original del problema, la cual, en muchos casos, es estratégica en la solución del mismo (ver ilustración 1). Otras medidas de centralidad pueden definirse, como veremos más adelante.

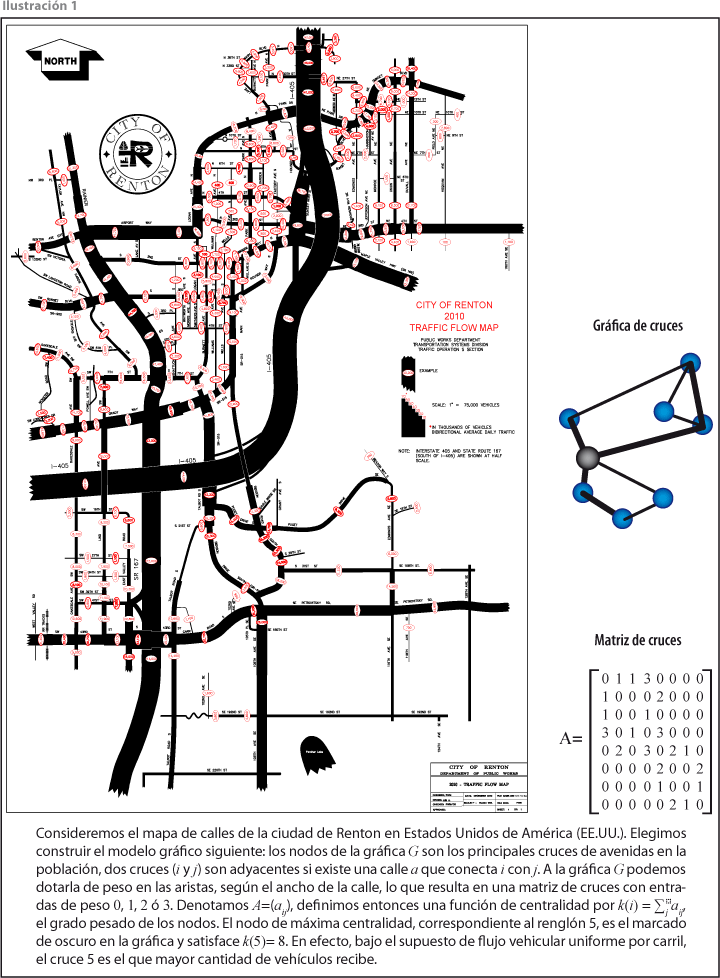
En la segunda parte del artículo desarrollamos algunos conceptos básicos que nos serán de utilidad a lo largo de las discusiones. Dos medidas de centralidad concentrarán nuestra atención: por cercanía, que determina el rango de proximidad de un nodo a los otros de la red; y la espectral, determinada de acuerdo con las coordenadas de un vector propio positivo llamado de Perron, asociado al valor máximo de la matriz considerada (por lo general, la de adyacencia o la de adyacencia pesada). Cabe mencionar que, como aportación original de este trabajo al estudio de la complejidad de las redes de transporte, hemos introducido el concepto coherencia de una red, que es una medida que indica si la estructura de la red de transporte está construida de acuerdo con los requerimientos reales. Un ejemplo típico es el aeropuerto de la ciudad de México, cuya jerarquía en la estructura de la red de rutas aéreas está rezagada de manera significativa respecto al volumen de pasajeros que mueve. Nuestros análisis darán expresión cuantitativa a estas vagas nociones cualitativas.

El siguiente apartado considerará el sistema de carreteras y aeropuertos de México para ilustrar el uso de la medida de centralidad por cercanía. Los elementos de la teoría de Perron y sus aplicaciones ocuparán la sección 4. La 5 considerará el sistema de transporte colectivo Metro y el de autobuses de la ciudad de México como ilustración de las diferentes medidas de centralidad desarrolladas. En todos los casos se determinará la eficiencia del sistema de transporte, esto es, qué tan cercano se encuentra el sistema de su estructura ideal, así como la coherencia de la red. En ocasiones, haremos referencia a artículos y libros matemáticos y desarrollaremos algunos argumentos matemáticos ilustrativos en los pies de página.

El concepto de las medidas de centralidad fue introducido en su inicio por A. Bavelas (1950), en el contexto de las ciencias sociales, en la década de los 50.¹ Se trata de uno de los términos más estudiados en el análisis de redes ya desde finales de la década de los 70 en el área de las redes sociales. Algunos autores han empleado las medidas de centralidad en relación con el flujo de información en diversas redes, así como de bienes usados, movimiento de dinero, propagación de rumores, correos electrónicos, diseminación de actitudes, propagación de infecciones y movimiento de paquetes.

Nuestros análisis de redes de transporte apuntan en dos direcciones: por una parte, resolvemos preguntas concretas de interés económico y social, con un sentido matemático preciso, que podrían multiplicarse de manera indefinida (¿qué carretera es más estratégica en el sistema carretero mexicano?, ¿la creación de qué rutas aéreas acercaría más a las 20 ciudades más grandes del país?, ¿la línea 12 del Metro está en el lugar donde más se le necesitaba?, ¿cuál es la eficiencia del sistema de autobuses urbanos de la ciudad de México y cómo se compara con otras ciudades?), e importantes y originales pueden ser las respuestas a estas preguntas, que son sólo ejemplos sencillos de la aplicación de las técnicas propuestas; por otra parte, esto se orienta hacia la segunda motivación (de carácter tanto político como académico) de este trabajo, la necesidad de crear un banco de información y una unidad nacional de análisis para la georreferenciación.

2. Gráficas y criterios de centralidad

Las gráficas son modelos matemáticos usados para representar los más variados sistemas: moléculas químicas donde los nodos simulan átomos y las aristas, enlaces eléctricos; sistemas carreteros, poblaciones y carreteras que las conectan; y redes de coautoría, científicos y los artículos escritos de forma conjunta, entre otros. A estas gráficas podemos dotarlas de pesos en sus aristas, así: los enlaces eléctricos entre átomos pueden representar el número de electrones compartidos por ellos, o bien, las carreteras es posible señalarlas por su longitud; en el tercer ejemplo, las coautorías pueden pesarse por el número de artículos escritos en conjunto por los científicos.

2.1. Matriz de adyacencia de una gráfica pesada y sus potencias

Dada una gráfica G con vértices {1,2,…,n}, supondremos que las aristas i - j tienen peso w_ij ≥ 0. Escribimos a_ij = 1 o a_ij = 0 para indicar que hay o no arista entre i y j. El peso w_ij = 1 no es necesario escribirlo de manera explícita, los pesos mayores que 0 se señalarán en cada arista de la gráfica. La matriz de adyacencia A(G) = (ɑ_ij) y la matriz de la red o pesada, A(G) = (w_ij) son arreglos numéricos de tamaño n × n (ver ilustración 2).

Dada una gráfica G con matriz de adyacencia A(G) = (a_xy) de tamaño n × n, el número de vecinos c(x) = ∑_y a_xy de x es la suma total del renglón x, de manera que el promedio del número de vecinos es:

Llamamos al número de caminos de longitud k que van de x a y. Observemos que se obtienen de la siguiente manera:

Por último, las potencias de A(G) son precisamente A(G)^k = ().
En general, trabajaremos con gráficas pesadas, esto es, suponemos que la gráfica G tiene asociada una función p que asigna a cada vértice x de G un número positivo p(x), llamado el peso de x. Ejemplo típico (que usaremos en este trabajo) asigna a las ciudades x que aparecen como nodos de la gráfica de carreteras del país su número de habitantes p(x) (ver ilustración 3).

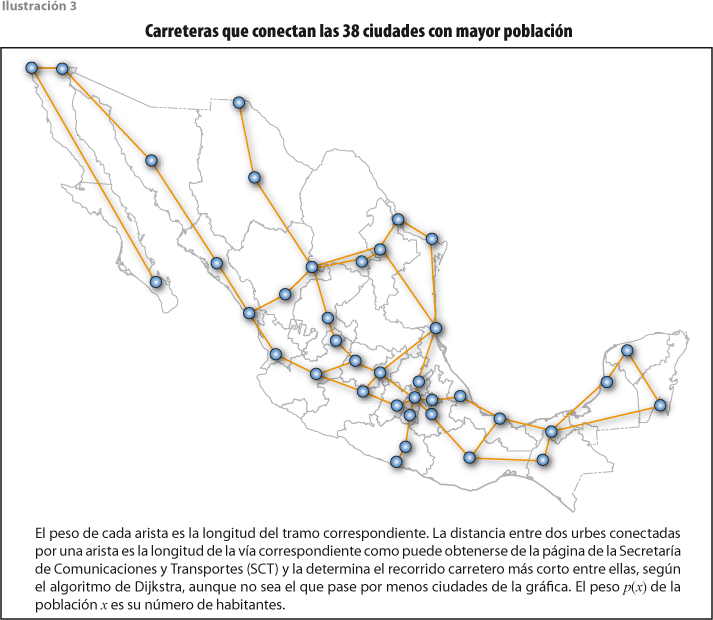
2.2 Distancia en una gráfica pesada

La distancia entre dos nodos en una gráfica es la longitud del camino más corto que los une. Si la gráfica tiene pesos, esa vía más corta puede pesar más que otra más larga (ver ilustración 4).

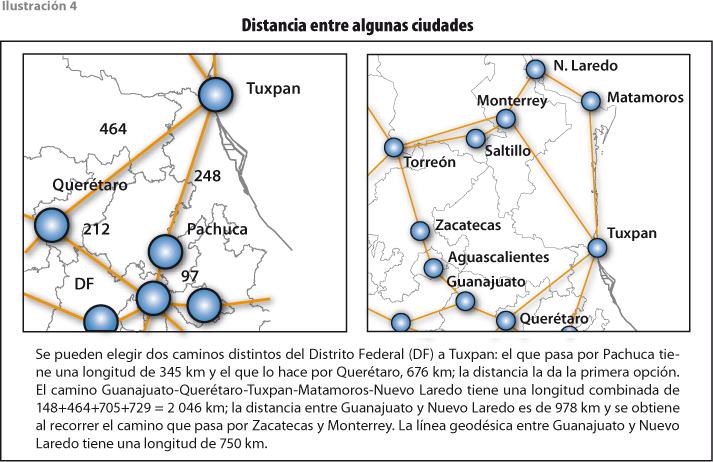
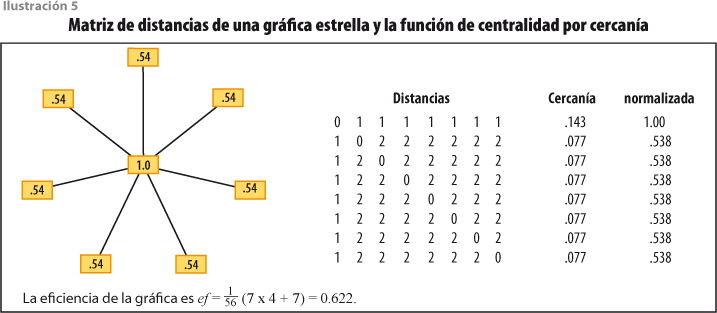
Encontrar el camino de menor peso que une dos nodos en una gráfica pesada no es siempre sencillo. Un procedimiento sistemático para encontrarlo y, con ello, calcular su distancia en una gráfica pesada es el algoritmo de Dijkstra, el cual permite calcular la distancia D(y) que separa un nodo fijo (x) de todos los demás de la gráfica conexa G. En efecto, comenzamos asignando valores D(y) = ∞ para y ≠ x, y D(x) = 0 e iremos modificando la función D hasta que exprese las distancias desde x. Decimos que un nodo y está marcado si la función D ha sido ya correctamente determinada en y. El algoritmo termina cuando todos los nodos están marcados.

En un paso intermedio, cuando no todos los nodos están marcados, elegimos un nodo z no marcado con D(z) mínimo posible (observe que en el primer paso, necesariamente z = x). Recorremos todos los nodos adyacentes de z, excepto los marcados, llamaremos a éstos, v. Si el valor D(v) de la pretendida distancia de x hasta v es mayor que la distancia desde x hasta z, sumada al peso d(z,v) de la arista entre z y v, entonces se redefine:

D(v) = D(z) + d(z, v)

Marcamos entonces el nodo z. La conexidad de G implica que todos los nodos quedan, al final, marcados.

2.3 Centralidad

Una función de centralidad (f_G) asigna un valor real positivo a cada nodo de una red G de manera que si g: G → G´ es un isomorfismo, entonces f_G(x) = f_G´(g(x)) para todo x nodo de G. De esta manera, la función de centralidad es un atributo estructural de los nodos en una red; en otras palabras, se trata de un valor asignado al nodo debido a su posición estructural en la red. Algunas medidas de centralidad consideradas en la literatura son:

• Grado pesado. Se trata de la primera y más simple definición de centralidad. Se define como el número de enlaces (con peso) que posee un nodo con otros. Suele representarse como k. El grado se interpreta a menudo como el número de conexiones que tiene un elemento de la red en ella.

• Por cercanía. De acuerdo con Freeman (1979), la cercanía c_G(x) de un nodo x a la red G es el promedio de la separación (definida como el inverso de la distancia entre ellos) de x a cada uno de los nodos de la red. En notación matemática:

donde n es el número de nodos en la red.

En una red carretera G, si suponemos que los automóviles se mueven a velocidad constante, a mayor longitud de una carretera menor cercanía entre los extremos. En este caso, c_G(x) se puede interpretar como el tiempo medio de llegada desde x hasta otra ciudad.

El modelo matemático correspondiente, que jerarquiza a los nodos de acuerdo con el valor de las coordenadas del vector propio de Perron, será desarrollado más adelante.

2.4 Eficiencia de una red

Continuando con la red como modelo de un sistema carretero, su eficiencia² es una medida del tiempo que emplea un vehículo que se desplaza en ella, asumiendo velocidad constante, y se calcula como la suma de los inversos de las distancias entre todos los pares de nodos, normalizado por el número total de pares que se pueden formar, esto es,

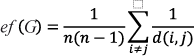
Como medida de la calidad de una red, ha sido utilizada en el estudio de la red neuronal y las de comunicación y transportación.

3. Sistemas carretero y de rutas aéreas de México

La red carretera del país constituye el andamiaje infraestructural que enlaza el sistema urbano de México y permite el intercambio físico de mercancías al conectar de manera funcional la oferta y demanda de los grupos humanos y las empresas localizadas en cada ciudad individual, lo cual hace posible la articulación de la vida nacional.

El patrón de distribución del sistema carretero tiene características bien definidas, que sigue los trazos principales de la red ferroviaria que le antecedió, es decir:³

• Se repite la estructura radial y concéntrica que favorece la jerarquía de la ciudad de México y de contadas urbes de segundo y tercer orden (Guadalajara, Monterrey, Aguascalientes y Mérida, por ejemplo).

• Continúan predominando los ejes longitudinales desde la capital hacia la frontera norte; se acentúa la debilidad de los vínculos hacia el sur y sureste y siguen faltando los ejes transversales.

• Se mantiene el aislamiento en el cual quedaron desde principio del siglo pasado las localidades de los territorios periféricos, que están representados por montañas, desiertos, selvas, costas y fronteras.

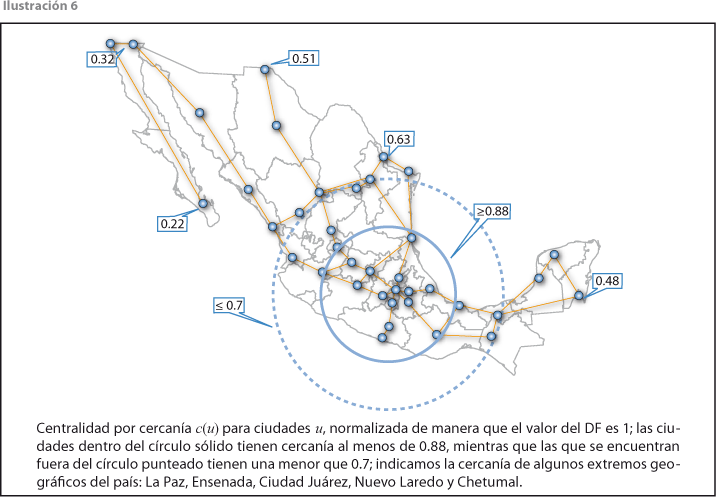
Muchas de las condiciones de centralismo y aislamiento de regiones del país pueden leerse en el mapa de valores de la centralidad por cercanía (ver ilustración 6), un ejercicio que nos contendremos de discutir de forma extensa. Señalamos sólo que la zona de alta accesibilidad carretera se centra en el corredor de las carreteras ciudad de México-Irapuato y ciudad de México-Guadalajara, extendiéndose a Querétaro, Guanajuato y el norte de Michoacán de Ocampo. Este patrón poblacional del sistema urbano principal acentúa las diferencias de accesibilidad y el peso de la zona centro en la articulación territorial del conjunto del país.

Por otra parte, el gobierno concede tal relevancia al desarrollo del sistema carretero que el Programa Nacional de Infraestructura 2007-2012 incluyó 100 proyectos estratégicos de caminos, entre ellos: 20 libramientos y accesos, 20 carreteras nuevas, 42 ampliadas y modernizadas, 15 interestatales y tres puentes fronterizos.

El Travel and Tourism Competitive Index ubicó a México como el cuarto destino más atractivo en el continente americano y el primero en América Latina. Los viajes y el turismo en el país representaron 6% del producto interno bruto en el 2012 y 7.2% del mercado laboral. Se estima,⁴ en años recientes, en 22.6 millones el número de turistas (internacionales y domésticos) en los aeropuertos mexicanos; sin embargo, el desarrollo de éstos y las rutas domésticas dejan mucho que desear.

Con la salida del mercado comercial de Mexicana de Aviación, la mayor parte de las rutas aéreas quedó en manos de Aeroméxico, que cuenta con una flota de 70 aviones Boeing; desde su centro en el Aeropuerto Internacional de la Ciudad de México opera 300 vuelos diarios a 32 ciudades en el país, 14 a EE.UU., dos a Europa, cuatro a Sudamérica y uno a Asia.

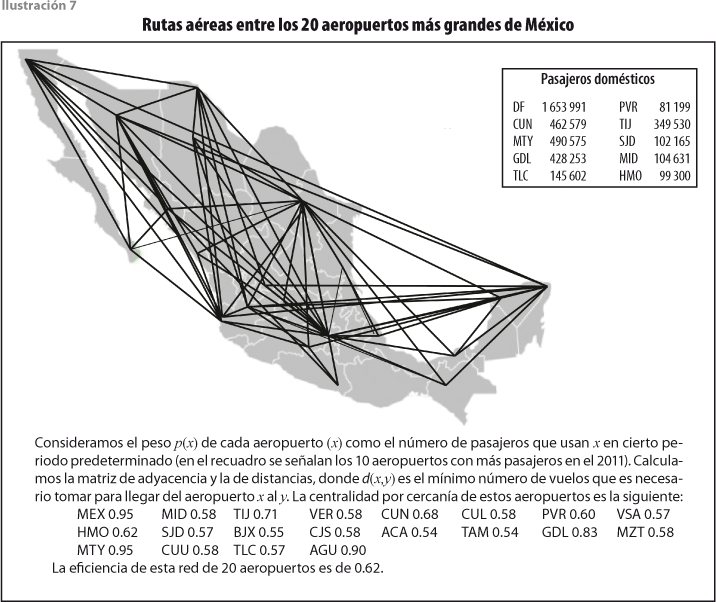
La característica principal de la red de rutas aéreas domésticas mexicanas (además del elevado costo de los pasajes) es la alta centralización de ésta. En efecto, basta observar que, en la red de los 20 aeropuertos principales, la ruta más frecuentada entre dos ciudades pasa por la ciudad de México, con las obvias consecuencias de incomodidades por tráfico aéreo y pérdida de horas de trabajo humano (ver ilustración 7). Esta condición de la red de rutas aéreas puede expresarse por medio de la matriz de distancias (d(x,y)) entre sus aeropuertos. En efecto, satisfacen que d(x,y) = 1 o d(x,y) = 2; el primer caso es si existe una ruta directa; el segundo, si sólo se puede llegar de x a y pasando por el aeropuerto en la ciudad de México.⁵

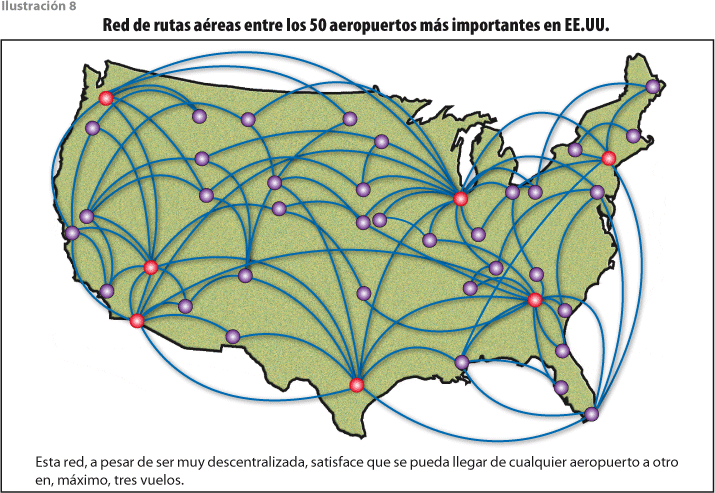
La existencia de un número pequeño⁶ k para una red tal que dos nodos cualesquiera de la red o bien no pueden conectarse o se conectan en, a lo más, k pasos se conoce como propiedad de mundos pequeños, cuyo nombre se refiere al experimento de Milgram (1967) que mostraba que dos personas en una gran ciudad se relacionan por una cadena de conocidos de, máximo, seis. Las redes de rutas aéreas que hemos considerado satisfacen la propiedad de mundos pequeños con k = 2 en el caso de México y k = 3 para Estados Unidos de América (ver ilustración 8).

4. Medida matemática de la complejidad de una red

Como parte esencial de las técnicas del análisis matricial se encuentra la determinación de los valores y vectores propios de matrices cuadradas y las múltiples aplicaciones a problemas de teoría de gráficas, probabilidad, economía e ingeniería.⁷

4.1. Valores y vectores propios de una matriz

Consideremos una matriz A = (a_ij) de tamaño n × n. Decimos que un vector u de tamaño n es vector propio de A si existe un número r tal que Au = ru.

Los valores propios son las soluciones numéricas de la ecuación Det (x id_n – A) = 0, que se llama ecuación característica de A, donde id_n es la matriz identidad de tamaño n × n. Una vez encontrados los valores propios para cada uno de ellos, digamos r, el correspondiente vector propio u es solución de la ecuación lineal:

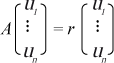
Si A es simétrica, esto es a_ij = a_ji, para todas las entradas 1 ≤ _i,j ≤ n, entonces hay n soluciones reales de la ecuación característica. En caso de que la matriz A sea no negativa, esto es, a_ij ≥ 0 para todas las entradas i,j, entonces hay valores propios r ≥ 0. El máximo de los valores propios:

r(A) = max {r : 0 ≤ r valor propio de A}

se llama el radio espectral de A.
Sea G una gráfica con n nodos, sea H una subgráfica de G que se obtiene de quitar un vértice x de G. Consideremos los valores propios de G:

y los valores propios de H:

El siguiente resultado se conoce como teorema de entrelazamiento de Weyl:

4.2 Teorema de Perron

En 1907, el matemático alemán Oskar Perron demostró el siguiente teorema:
Sea A = (a_ij) una matriz no negativa y sea r su radio espectral, entonces:⁸

(1) r es valor propio de A;

(2) existe un vector propio u de A tal que Au = ru y todas las entradas de u son no negativas;

(3) si A es la matriz de adyacencia de una gráfica conexa entonces valen:

(1') r es raíz simple del polinomio característico de A y

(2') el vector u tiene todas sus entradas > 0.

Si G es una gráfica conexa y A es su matriz de adyacencia, los valores u(x) para x nodo de G determinan la función de centralidad espectral. Interpretamos u(x) como una medida de la complejidad de la red G en el nodo x.

La jerarquía determinada por la centralidad espectral tiene múltiples aplicaciones; por ejemplo, en esencia es la jerarquía usada por el algoritmo PageRank que determina el orden de las respuestas en las consultas al buscador de Google (ver ilustraciones 9 y 10).

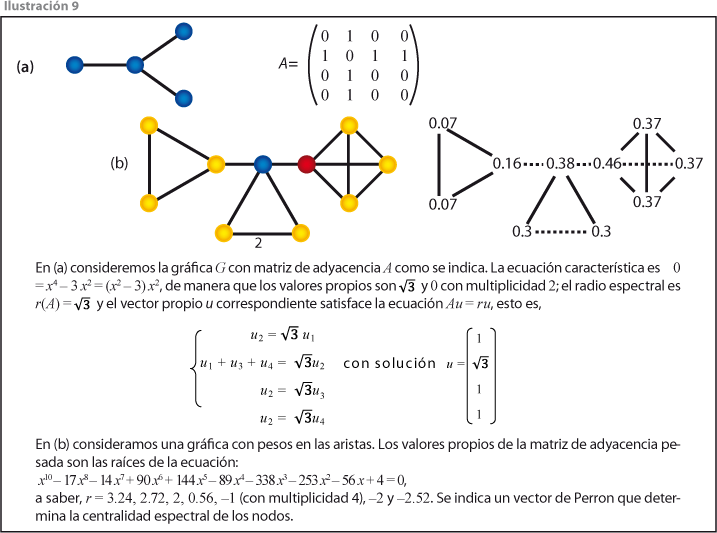
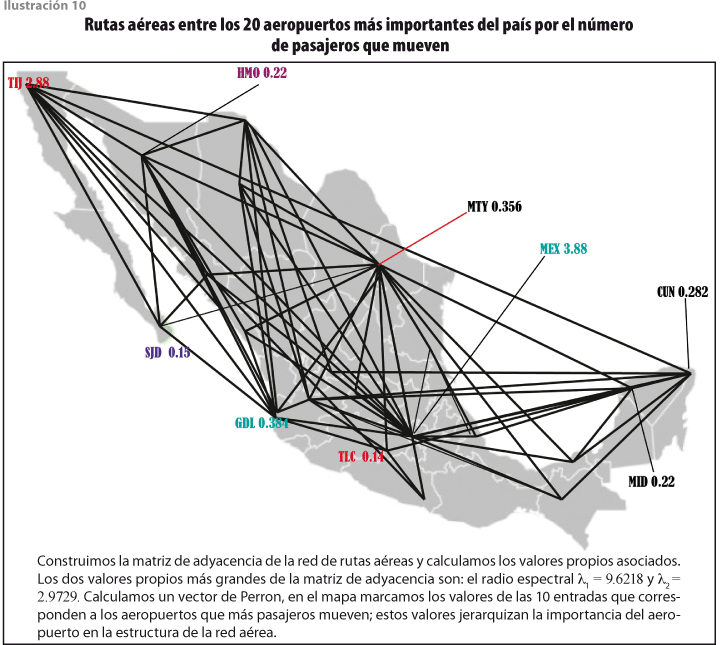
4.3 Coherencia de las redes de transporte

Consideremos, una vez más, la red del sistema carretero. Ahora, recordemos que a los nodos les hemos asignado como peso p(x) el número de habitantes de la ciudad x. Por otra parte, hemos obtenido una medida de la complejidad de la red en x por medio de un vector de Perron u. Es natural esperar que una ciudad grande tenga un lugar importante en la estructura global de la red, esto es, esperaríamos que:

si p(x) > p(y) entonces u(x) > u(y).

Veamos cómo se comparan estos valores (ver tabla 1). Usamos, por un lado, la población de las 10 zonas metropolitanas más pobladas de México, según el Censo de Población y Vivienda 2010 (INEGI) y, por el otro, los valores de centralidad espectral calculados como las coordenadas de un vector de Perron u. El cociente es una medida de comparación entre las dos funciones de centralidad u y p; sin embargo, cada función está cuantificada en diferentes unidades, por lo que es necesario normalizar con respecto al promedio . A la función de centralidad definida por:

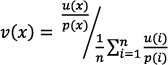
la llamaremos centralidad comparada.

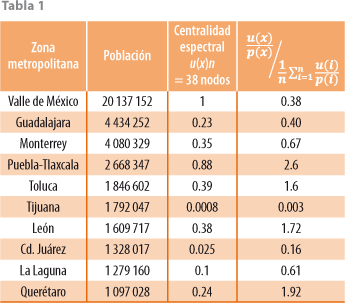
Nodos x satisfaciendo v(x) ≥ 1corresponden a ciudades que tienen una jerarquía en la red carretera, relativa a la población que sustentan, por arriba de la media nacional. En esas ciudades, y los respectivos nodos, diremos que la red carretera está bien desarrollada.

Los valores numéricos obtenidos confirman la impresión cualitativa de un mayor desarrollo en la región centro del país, que va de Puebla a León, pasando por Querétaro, Toluca y la ciudad de México. Esta última, cuando se considera su área urbana de 8.8 millones de habitantes, resulta en un valor de centralidad comparada de 0.95, muy arriba del de 0.38 que resulta de considerar la población suburbana.

Una medida de la desviación entre el desarrollo de la infraestructura de la red G de carreteras y las necesidades p de la población de las ciudades está dada por la desviación estándar de los valores de la centralidad comparada respecto a 1:

Definimos la coherencia de la red G como:

.

Es fácil ver que la coherencia satisface las siguientes propiedades:

• 0 < coh (G) = ≤1

• coh (G) = 1 si y solamente si p = ku para alguna constante k > 0,esto es, el vector de pesos p es un vector de Perron para la matriz de adyacencia (pesada) de G.⁹

• A mayor coherencia, la estructura de la red se aproxima mejor a las necesidades de la población.

Para la red carretera, la desviación estándar es (G) = 0.83 que determina una coherencia coh (G) = 1/1 _{+ (G)} = 0.54.

El ejercicio correspondiente a la red de rutas aéreas con la función de peso p(x) de los aeropuertos definida por el número de usuarios de vuelos nacionales en el 2011 resulta en la tabla 2.

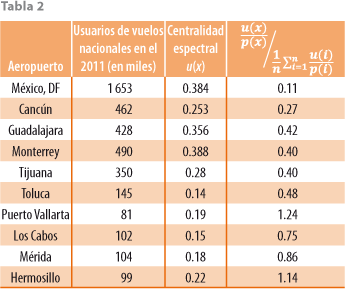
Los cálculos indican que la estructura de la red aérea no responde a los requerimientos de pasajeros en los aeropuertos del centro del país (DF, Guadalajara, Monterrey y Toluca) y en Cancún, mientras que la red está bien desarrollada en otros puertos turísticos. En el contexto global, la desviación estándar es de 0.55 y la coherencia de la red, de 0.64, lo cual muestra mayor coherencia de la red de transporte aéreo en México en comparación con la carretera.

5. Transporte en la ciudad de México

El Distrito Federal es la ciudad capital de los Estados Unidos Mexicanos y cuenta con una población de 8 851 080 habitantes (la Zona Metropolitana del Valle de México tiene 20 137 152 pobladores), según el censo más reciente. La mayoría de ellos utilizan a diario la red de transporte público para viajar desde sus hogares a los centros de trabajo, educativos o de entretenimiento, la cual está formada por distintos medios, como: el tren ligero, el transporte colectivo concesionado, trolebús, las Rutas de Transporte Público (RTP) del gobierno, el Metro (tan sólo este medio, según cifras oficiales, transportó en el 2010 a más de 1 410 millones de usuarios) y el Metrobús, entre otros.

Estas vías de transporte componen una red en la que, cada día, se realiza 78.5% de los viajes de la ciudad. El resto se hace en vehículos privados, siendo el automóvil particular el más usado. En cuanto al transporte público, la mayor parte de los traslados se realizan en microbuses (44.55%), seguido de los taxis (11%) y el Metro (5%).¹⁰ La integración de cada uno de estos modos para generar una red multimodal es muy baja, ya que los diferentes sistemas han crecido de forma independiente, sin ninguna planeación concertada. En consecuencia, no existe un sistema de pago integrado que facilite a los usuarios prepagar sus pasajes y abordar con facilidad a cada uno. Los que sí lo tienen (como el Metro, los trenes ligero y suburbano, el metrobús y el mexibus) no son compatibles, lo cual incrementa los costos de transacción.

El Metro cuenta con una red pequeña en kilómetros (201), pero con una enorme capacidad de transporte anual. Cuenta con 11 líneas (la 12 está en construcción) con un total de 175 estaciones de las cuales: 112 son de paso; 41, de transbordo y 22, terminales (11 de ellas son de transbordo). Está construido de forma subterránea, superficial y viaducto elevado: 106 estaciones son subterráneas; 53, superficiales y 16, en viaducto elevado.

Consideramos la gráfica G de estaciones del Metro (ver ilustración 11), sin la línea 12 (donde resulta una con 35 estaciones) y la G₁₂ donde ya la incluye (y da como resultado una con 40 estaciones). Para ambas, el peso de una arista x — y es la distancia, medida en número de estaciones, que separa a los vértices x,y. Podemos observar que:

• La nueva línea reduce la distancia entre varias estaciones, tal es el caso de los vértices correspondientes a Universidad y Tasqueña: sin la línea 12, la distancia mínima era de 19 y con la nueva es de 10.

• La eficiencia de la gráfica G₁₂ es de 0.14, esto es, si suponemos que toma un minuto moverse entre dos estaciones del Metro, desde una de las 40 seleccionadas en G₁₂, se harán, en promedio, siete minutos en llegar a otra terminal en G₁₂.

• El radio espectral de la gráfica G es α=3.7828. Los primeros cuatro valores propios ordenados de mayor a menor son: 3.78, 3.16, 3.03 y 2.96.

• Los nodos más importantes de G, según la centralidad espectral son:

28. Chabacano.

23. Pino Suárez.

22. Salto del Agua.

18. Bellas Artes.

24. Candelaria.

• El radio espectral de la gráfica G₁₂ es ß=3.8518. Los primeros cuatro valores propios ordenados de mayor a menor son: 3.85, 3.22, 3.12 y 2.99.

• Los nodos más importantes de G₁₂, según la centralidad espectral son:

28. Chabacano.

22. Salto del Agua.

23. Pino Suárez.

27. Centro Médico.

29. Jamaica.

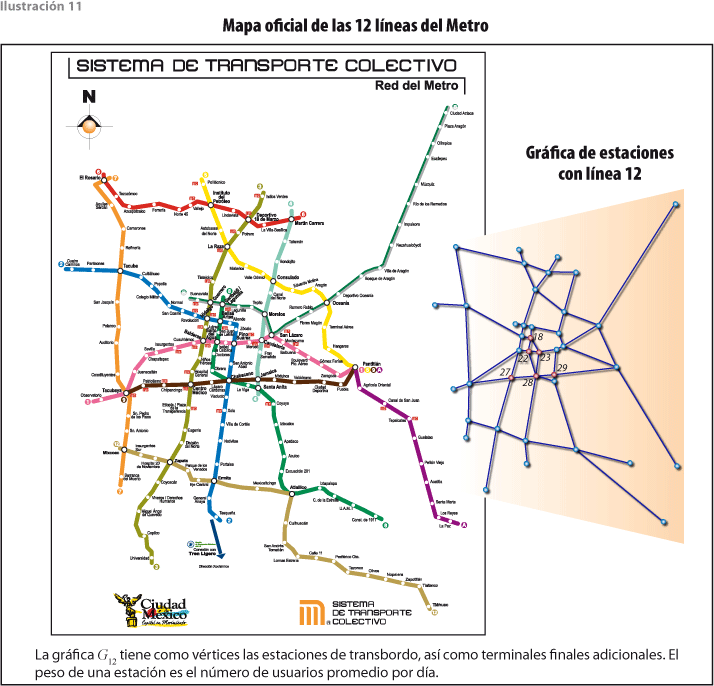
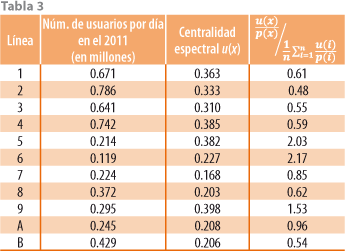
El número de pasajeros que mejor se conoce es el de usuarios de las diferentes líneas del Metro; su promedio por día (en el 2011) de las diferentes líneas se puede apreciar en la tabla 3.

Con esta idea en mente, introducimos la gráfica de líneas (ver ilustración 12), que tiene 12 vértices, siendo i, j adyacentes si hay una estación de transbordo entre las líneas i y j.

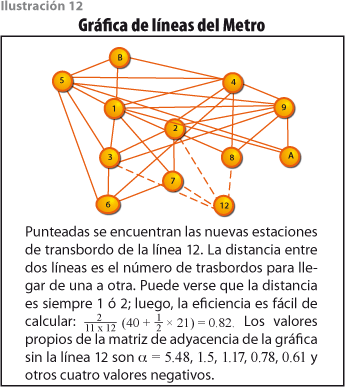
El radio espectral de la gráfica G de líneas de Metro, sin la línea 12, es α = 5.48 con vector de Perron asociado u, como se indica en la tabla 3. El valor medio de la centralidad comparada es:

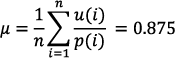
Resulta una desviación estándar de 0.58 y una coherencia de 0.62, un resultado similar al de las rutas aéreas a nivel nacional.

Como hemos mencionado antes, el movimiento de transporte de pasajeros en la ciudad de México se realiza sobre todo a través de microbuses concesionados, pero éstos no funcionan como una red de transportes pues cada ruta se encuentra compuesta por un grupo de concesionarios individuales que no funcionan como una empresa.
Consideramos la gráfica de microbuses (ver ilustración 13) con las siguientes características:

• Cuenta con un total de 20 nodos.

• La distancia más grande que se recorre entre nodos es de 17.24 km (usando la ruta óptima).

• La distancia más corta que separa dos nodos es de 1.05 km (un solo movimiento).

• El diámetro de la gráfica es 6.

• El radio geográfico de la región que envuelve la gráfica es de 13.28 km, obtenido de una medición con Google Earth.

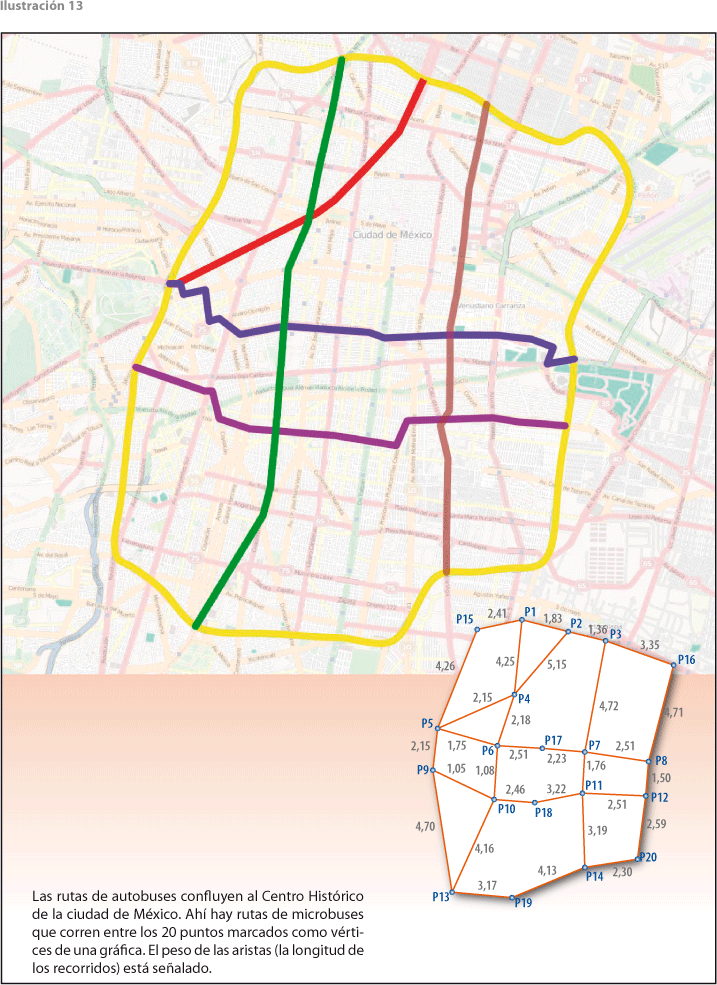
Trabajando las rutas en la gráfica de microbuses de manera integrada no es difícil diseñar un sistema satisfactorio, esto es, que cumpla lo siguiente:

1) Que en cada punto de la red se despachen autobuses en horarios bien definidos.

2) Que en todo momento, el número de autobuses en la ruta sea suficiente para cubrir la demanda de transporte.

Podemos formular el problema así: supongamos que se estima que en la hora t + 1 del día habrá p(x) pasajeros en el punto x de la red de microbuses, ¿cuántos autobuses a(x,y) de b pasajeros habrá que despachar del punto x hacia y en la hora t?

En efecto, para cada dos puntos x, y vecinos en la red G de microbuses consideremos su distancia d(x,y). Suponemos que todos los autobuses, en todas las rutas, se mueven a velocidad constante c.

Definimos la matriz de adyacencia A, cuya entrada ɑ_xy es 1 si x, y son vecinos y 0 si no lo son. La matriz A es no negativa y conexa, luego, el teorema de Perron garantiza que el radio espectral r > 0 es valor propio con vector propio asociado u con todas las entradas positivas. Hacemos:

en realidad, como no hay autobuses fraccionarios, debe tomarse el siguiente entero más grande que este número. Despachamos b(x,y) autobuses de b pasajeros del punto x hacia y en la hora que corre de t – c^–1 d(x,y) a t +1 – c^–1 d(x,y). Verificamos que en el intervalo t a t +1 en el punto x se reciben, al menos,

autobuses, con capacidad para, al menos, p(x) pasajeros.
Efectuamos los cálculos de la red de microbuses en la ciudad de México, resultando el radio espectral r = 3.26. Otros valores propios son 2.73, 2.41, 1.74, 1.42, 1.07 y los demás menores a 1. Un vector de Perron u determina la centralidad espectral como se muestra en la tabla 4 e ilustración 14.

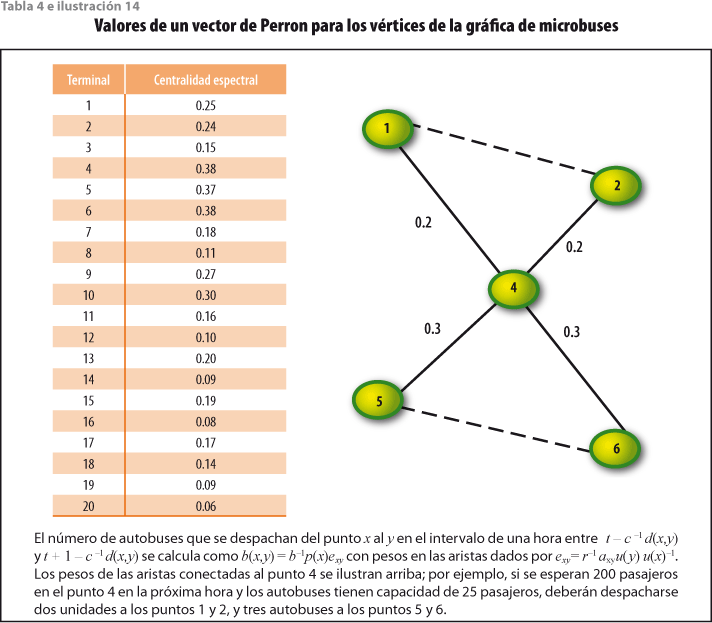
El ejemplo de la tabla 4 e ilustración 14 muestra que, funcionando de manera concertada, el sistema de transporte urbano puede enfrentar los diversos problemas que sufre: de administración, mantenimiento, accesibilidad, cobertura, horarios y seguridad. Puede, en fin, ser eficiente y coherente tanto en el sentido del lenguaje cotidiano como en el técnico que hemos introducido. Ejemplos en Latinoamérica como el de Curitiba en Brasil o el de Bogotá en Colombia demuestran que el mejoramiento del sistema de transporte público puede hacerse rápido y de forma barata, beneficiando a la población y transformando la ciudad.

Referencias

Bavelas, A. "Communication patterns in task-oriented groups", en: Journal of the Acoustical Society of America. 22, 723-730, 1950.
Bavelas, A. and M. Barrett. "An experimental approach to organizational communication", en: Personnel. 27, 386-397, 1951.
Barabási, Albert-László. Linked: How Everything Is Connected to Everything Else and What it Means for Business, Science, and Everyday Life. 2002.
Barabási, Albert-László and Albert Réka, "Emergence of scaling in random networks", en: Science. 286: 509-512, 1999.
Barabási, Albert-László, Mark Newman and Duncan J. Watts. The Structure and Dynamics of Networks. 2006.
Borgatti, Stephen. "Centrality and network flow", en: Social Networks. 27 55-71, 2005.
Chias, Luis, Héctor D. Reséndiz y Juan Carlos García Palomares. "El sistema carretero como articulador de las ciudades", en: Los grandes problemas de México II. Desarrollo urbano y regional. El Colegio de México, 2010.
Cvetkovic, D., Doob, M. and H. Sachs. Spectra of Graphs-Theory and Applications. Academic Press, 1980.
De la Peña, José A. Algebra lineal avanzada. Fondo de Cultura Económica, 1996.
Freeman, L.C. "Centrality in networks: I. Conceptual clarification", en: Social Networks. 1, 215-239, 1979.
Eke Eijgelaar, Paul Peeters and Pieter Piket. Domestic and International Tourism in a Globalized World. Research in Progress Paper. 2008.
Freeman, L.C., S.P. Borgatti y D.R. White. "Centrality in valued graphs: a measure of betweenness based on network flow", en: Social Networks. 13, 141-154, 1991.
Gantmacher, F.R. The theory of matrices. Vol. II. Chelsea, New York, 1974.
Latora, Vito and Massimo Marchiori. "Efficient Behavior of Small-World Networks", en: Physical Review Letters. Vol. 87, num. 19, 2001.
Lin, N., P. Dayton & P. Greenwald. "The urban communication network and social stratification: A 'small world experiment'", en: B. D. Ruben. Communication yearbook. Vol. 1,107-119. New Brunswick, Transaction Books, 1978.
Medina, Salvador. El transporte público en la ciudad de México: incentivos a la ineficiencia. Distintas Latitudes, 2011.
Milgram, S. "The small-world problem", en: Psychology Today. 1,61-67, 1967.
Watts, D. J. & S. H. Strogatz. "Collective dynamics of 'small-world' networks", en: Nature. 393, 440-442, 1998.
www.distaciaentreciudades.com, para la información sobre carreteras.
www.inegi.org.mx/, www.sct.gob.mx/, http://es.wikipedia.org/wiki/Anexo: Aeropuertos_en_México y www.dices.net/aeropuertos/distancias.html para la información sobre aeropuertos.
INEGI. Encuesta Origen-Destino 2007. Zona Metropolitana del Valle de México. www.setravi.df.gob.mx/wb/stv/cinco_siglos_de_transporte_en_la_ciudad_de_mexico_
www.metro.df.gob.mx

¹ Y luego aplicadas en experimentos conducidos por Bavelas y sus estudiantes Leavitt y Barret, ver Bavelas, A. and Barrett, M. (1951).
² El concepto fue introducido en Latora, Vito and Massimo Marchiori (2001).
³ L. Chias et al. (2010).
⁴ Eke Eijgelaar, Paul Peeters and Pieter Piket (2008).
⁵ Estas características estructurales se reflejan en los valores propios de la matriz de adyacencia, como veremos en la próxima sección. También, permite el cálculo inmediato de la eficiencia de la red. En efecto, d(x,y) = 1 para las 80 rutas marcadas en el mapa y d(x,y) = 2 para las 300 parejas (x,y) no unidas en el mapa. Así, la eficiencia