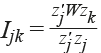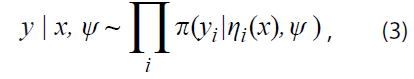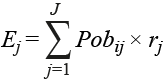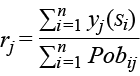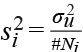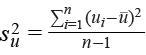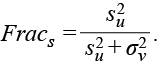Modelación espacial bayesiana de la pobreza y el gasto social en municipios de Chiapas a través de INLA

Bayesian Spatial Modeling of Poverty and Social Spending
in Municipalities of Chiapas through INLA

 

Gerardo Núñez Medina
El Colegio de la Frontera Norte, gnunez@colef.mx

 

Vol. 13, Núm. 1 Epub                                                                     Modelación espacial... Epub

 

El trabajo tiene por objetivo modelar la distribución espacial de la pobreza municipal en Chiapas a partir del efecto que ejerce el gasto social; para ello, se ajusta un modelo de regresión gaussiano estructurado latente que utiliza como variable dependiente la pobreza y como independiente, el gasto social. La finalidad es identificar patrones espaciales no aleatorios de pobreza que resultan de la confirmación de conglomerados espaciales de concentración de pobreza en el que los efectos generados por el gasto social resultan ser estadísticamente significativos; sin embargo, su peso relativo fue marginal. Palabras clave: campo aleatorio markoviano; inferencia bayesiana; INLA; Índice de Moran.

The objective of this paper is to model the spatial distribution of municipal poverty in Chiapas based on the effect of social spending; for this purpose, a latent structured Gaussian regression model is fitted using poverty as a dependent variable and social spending as an independent variable. The aim is to identify non-random spatial patterns of poverty resulting from the confirmation of spatial clusters of poverty concentration in which the effects generated by social spending turn out to be statistically significant; however, their relative weight was marginal. Key words: Markovian random field; bayesian inference; INLA; Moran Index.

Recibido: 19 de abril de 2021.
Aceptado: 2 de julio de 2021.

 

Introducción

El objetivo del trabajo es modelar la distribución espacial de la pobreza municipal en Chiapas utilizando como variable explicativa el gasto social. La hipótesis sostiene que existe una relación directa entre el nivel ejercido de gasto social y la pobreza municipal observados, los cuales se encuentran espacialmente correlacionados. Es importante aclarar que no se busca realizar una evaluación de la eficiencia del gasto social, sino cuantificar los niveles de asociación espacial entre las variables señaladas para los municipios de Chiapas al 2015.

La importancia de esta investigación se orienta en que Chiapas es la entidad federativa con los mayores niveles de pobreza en el país. El Consejo Nacional de Evaluación de la Política de Desarrollo Social (CONEVAL) estimó que 72.5 % de la población vivía en esta condición y 29.9 %, en condición de pobreza extrema en el 2015 (CONEVAL, 2017), y el gasto social en el estado es uno de los más elevados de todo México (CEFP, 2015). El Ramo 33 representó 48.1 % de los recursos totales ejercidos por el gobierno estatal en el mismo año.

La información utilizada a lo largo del trabajo es resultado de la concatenación de dos bases de datos: la primera del CONEVAL, de donde se obtuvieron las mediciones de pobreza municipal, y la segunda de la Secretaría de Planeación, Gestión Pública y Programa de Gobierno (SPGPPG) de Chiapas, de cuya página se recopilaron las cifras relativas al gasto social municipal del Ramo 33, en particular del Fondo de Infraestructura Social Municipal ejercido por los municipios durante el 2015.

La medición de la pobreza en México hasta antes del 2010 se hacía tomando como dimensión principal el ingreso, lo que permitía clasificarla en tres líneas principales: 1) pobreza alimentaria, 2) pobreza de capacidades y 3) pobreza de patrimonio. Esto cambió en el 2010 debido a que la Ley General de Desarrollo Social ordenó que su estimación se realizará con un enfoque multidimensional, el cual considera que una persona se encuentra en condición de pobreza cuando su ingreso se encuentra por debajo de la línea de bienestar mínimo y presenta rezagos o carencias en, al menos, uno de sus derechos sociales (CONEVAL, 2014). La línea de bienestar mínimo distingue a la población que no tiene los ingresos suficientes para adquirir los alimentos necesarios para contar con una nutrición adecuada, incluso si usara todo su ingreso para comprarlos, mientras que la línea de bienestar identifica a aquella población que no posee los recursos suficientes para adquirir los bienes y servicios que requiere para satisfacer sus necesidades tanto alimentarias como no alimentarias (CONEVAL, 2012). Para fines de esta investigación, se utilizó la medición de pobreza multidimensional, en particular el porcentaje de población en condición de pobreza.

Los datos referentes al gasto social municipal provienen del Fondo de Aportaciones para la Infraestructura Social Municipal (FISM), que forma parte del Ramo 33. Los fondos de este son recursos que la Federación transfiere a los estados y a los municipios, cuyo gasto está condicionado a la consecución y cumplimiento de objetivos en áreas prioritarias para el desarrollo nacional, como el combate a la pobreza y la construcción de infraestructura. Los fondos del Ramo 33 son ocho;^[1] y de ellos, el Fondo de Aportaciones para la Infraestructura Social (FAIS) se divide en dos partes, estatal, Fondo de Aportaciones para la Infraestructura Social Estatal (FISE), y municipal, Fondo de Aportaciones para la Infraestructura Social Municipal (FISM). Es el único fondo que es ejercido directamente por los municipios,^[2] por lo que tiene un efecto territorial medible y diferenciable.

La hipótesis planteada sostiene que existe una relación causal entre los niveles de pobreza y gasto social, misma que es observable y medible en el plano geográfico y que a partir de métodos estadísticos espaciales es posible identificar patrones no aleatorios de asociación espacial entre la pobreza y el gasto social (Barrientos et al., 2008; Barro, 1991). Para ello, se aplicaron técnicas de análisis exploratorio de datos espaciales (AEDE) y de modelación espacial bayesiana, en particular modelos de regresión bayesiana ajustados a través de la aproximación anidada integrada de Laplace (INLA).

Las relaciones establecidas por distintos marcos teóricos señalan que existe un encadenamiento causal entre el gasto social y la pobreza (Cortés, 2009). El primero se entiende como la erogación destinada a la implementación de políticas públicas dirigidas a atender las necesidades de las personas con menores ingresos, en las regiones con menos recursos y grupos sociales desprotegidos (López & Núñez, 2016), por lo que es considerado uno de los principales instrumentos redistributivos de recursos en la sociedad y el componente más importante del Estado para incidir en la distribución del ingreso, es decir, que uno de los efectos más importantes esperados del gasto social es su capacidad para modificar la distribución del ingreso y, por lo tanto, reducir los niveles de desigualdad y pobreza observados al interior de una sociedad (Ferreira, Leite & Ravallion, 2010).

 

Análisis espacial de la pobreza y el gasto social en Chiapas

El trabajo estadístico inicia con un estudio exploratorio de datos que tiene por objetivo identificar patrones de agrupamiento espacial, detectar la presencia de estructuras o advertir la existencia de valores aberrantes espaciales a través de estadísticos, diagramas, gráficas y mapas (Chasco, 2003). Una de las primeras formas para detectar patrones de asociación espacial surgió a partir del postulado establecido por Tobler (1970) en su primera ley que dice: “… todo está relacionado con todo, pero las cosas cercanas están más relacionadas que las cosas distantes…”. Esta sienta las bases para definir el concepto de autocorrelación espacial como una medida de asociación entre unidades espaciales respecto de los valores alcanzados por un atributo o variable previamente definida.

El Índice de Moran es un estadístico que estima el nivel de autocorrelación espacial. En su versión global, mide la correlación que hay entre la variable y el espacio geográfico, conformado por todas las regiones analizadas al unísono.^[3] Evalúa la existencia de un patrón de agrupación, dispersión o aleatorio y devuelve valores entre -1 y +1, lo que permite reconocer conglomerados de unidades espaciales (Anselin, 1995) en cinco categorías: 1) low-low: unidades con valor inferior al promedio, rodeadas de unidades con valores por debajo de la media del atributo de interés que corresponden a conglomerados llamados zonas frías; 2) low-high: unidades espaciales con valor por debajo del promedio rodeadas por unidades con valores por encima del promedio de la variable de interés; 3) high-low: unidades espaciales con valor por arriba del promedio rodeadas por unidades con valores por debajo del promedio de la variable de interés; 4) high-high: unidades con valor por encima del promedio rodeadas de unidades con valores por arriba de la media de la variable de interés; corresponden a conglomerados denominados zonas calientes; 5) no significant: el conjunto de unidades espaciales donde la variable no presenta niveles de correlación estadísticamente significativos respecto de  sus vecinos (Getis & Ord, 1992).

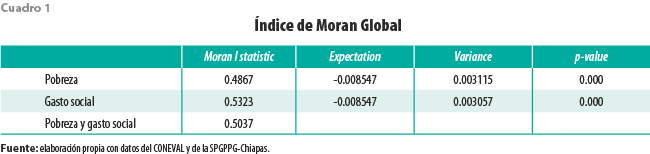
Los resultados de las estimaciones del Índice de Moran para los niveles pobreza y gasto social municipal se muestran en el cuadro 1 e indican que existe autocorrelación espacial global con un nivel de significancia estadística superior a 5 % para ambas variables, y que representan altos índices de autocorrelación espacial (Cressie, 1993); en los dos casos, los niveles de autocorrelación resultaron ser estadísticamente significativos (el p-value asociado < 0.01, ver cuadro 1), lo que permite suponer la presencia de relaciones espaciales capaces de explicar los niveles de pobreza municipal a lo largo de todo Chiapas.

 

 

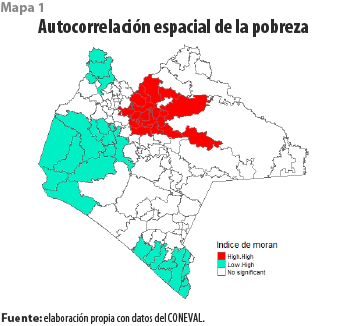
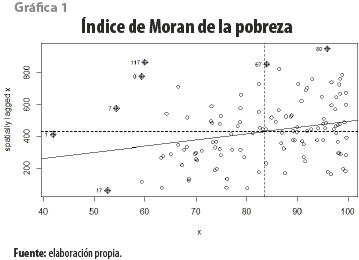
La pendiente de la recta de regresión observada en la gráfica 1 representa el valor del Índice de Autocorrelación Espacial Local de Moran para la población en pobreza (0.486); a mayor pendiente se tendrá un nivel más elevado de autocorrelación espacial, mientras que el mapa 1 representa la correlación espacial local de la pobreza municipal de acuerdo con la clasificación establecida por el mismo Índice (Cliff & Ord, 1981). En el mapa es posible identificar un conglomerado caliente, es decir, un conjunto de municipios con altos niveles de pobreza rodeados de otros con niveles de pobreza por encima de la media estatal; además, se distinguen tres conglomerados fríos, donde la presencia de pobreza es baja y que están rodeados de municipios con bajos niveles de incidencia de pobreza.

 

En Chiapas, desde la década de los 90, la política social se ha convertido en el componente más importante de la política pública con dos fondos fundamentales: 1) el fondo Ramo 33 y 2) el fondo Ramo 20, de subsidios y transferencias destinados al desarrollo social. Ambos son ejercidos desde los niveles federal y estatal, mientras que el FISM es un fondo destinado al financiamiento de obras, acciones sociales e inversiones municipales dirigidas a atender rezagos en áreas como: agua potable, alcantarillado, electricidad, caminos rurales, infraestructura básica de salud y educativa, así como mejoramiento de vivienda.

A diferencia de los fondos señalados, 80 % del FAIS debe ser transferido directamente a los municipios a través del FISM, de forma que este tiene la capacidad para transformar el entorno social y económico de un área geográfica específica a partir de generar condiciones de bienestar que reduzcan los niveles de pobreza al mejorar el acceso a bienes y servicios públicos.

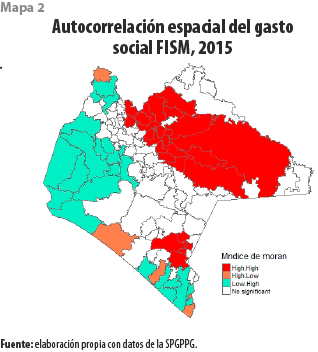
El mapa 2 muestra la distribución espacial del gasto social municipal (FISM) analizado a través del Índice de Moran; en este se observan cinco conglomerados, dos de alto y tres con bajo gasto social, es decir, dos zonas calientes y tres frías. Los conglomerados fríos se localizan, dos en la región costa y uno en la frontera con Tabasco y agrupan a los municipios donde el gasto social ejercido se encuentra por debajo del gasto promedio del estado, para el mismo ramo y año.

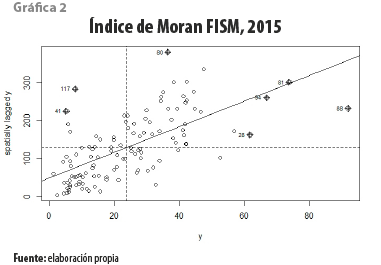
La pendiente de la recta de regresión, en la gráfica 2, representa el valor del Índice de Moran Global de autocorrelación espacial positiva (0.532) y estadísticamente significativa para el gasto social municipal (FISM). Es notoria la presencia de cinco municipios, en el cuadrante I, que están altamente correlacionados de forma positiva: Chiapilla, Siltepec, Simojovel, Sunuapa y Teopisca, lo cual significa que reciben montos per cápita significativamente superiores a los que se esperaría en relación con los recibidos por municipios vecinos. En contraste, en la misma región destaca el municipio de Yajalón, que no está correlacionado espacialmente con sus vecinos en términos de lo que a gasto social se refiere.

 

De manera adicional, se estimó la correlación espacial entre la pobreza y el gasto social con la finalidad de establecer la evidencia para el posterior desarrollo de un modelo de regresión gaussiano latente. El concepto de autocorrelación espacial bivariada busca medir el grado de asociación sistemática entre una variable x_j observada en una ubicación determinada y su relación con una variable x_k observada en ubicaciones vecinas. El coeficiente de correlación espacial bivariado de tipo Moran entre dos variables se define como:

donde z_j y z_k son la versión estandarizada de x_j y x_k, de forma que tienen media 0 y varianza 1; W es la matriz de pesos espaciales estandarizada por renglones que define el conjunto de vecinos de cada observación. Dado que las variables z están estandarizadas, la suma de cuadrados utilizada en el denominador es una constante igual a n.

 

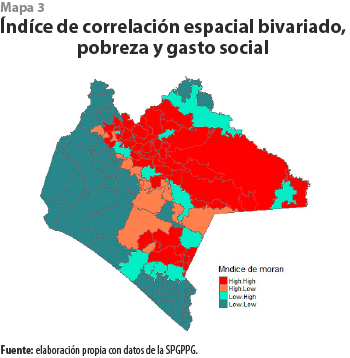
En el cuadro 1 puede verse la correlación espacial bivariada entre la pobreza y el gasto social, la cual fue de 0.50, lo que implica la existencia de un alto grado de correlación. El mapa 3 muestra la asociación entre los niveles de pobreza observados en el municipio i y el rezago espacial, correspondiente al gasto social ejercido en los municipios de la misma área geográfica; muestra dos conglomerados donde coinciden altos niveles de pobreza con altos niveles de gasto social, además de dos conglomerados donde la relación se registran bajos nivel de pobreza y de gasto social; en general, los conglomerados coinciden con las regiones de gasto social, no así con las de pobreza.

 

Metodología

Los modelos de regresión gaussianos estructurados latentes suelen definirse en tres capas: 1) hiperparámetros, 2) campo gaussiano latente y 3) función de verosimilitud (Rue, Martino & Chopin, 2009). Esta última maximiza la probabilidad de ocurrencia del vector de parámetros condicional a los datos observados y, generalmente, se modela utilizando una familia de tipo exponencial; en nuestra investigación se utilizó una distribución Poisson. El campo gaussiano latente se liga a la función de verosimilitud a través de una función de enlace dada por:

,

donde Y es el vector de observaciones; en nuestro caso representan los niveles de pobreza municipales; η es el predictor lineal; y h, la función de enlace. En términos generales, INLA está centrado en el cálculo de las distribuciones marginales a posteriori de los efectos latentes y de los hiperparámetros, en lugar de concentrarse en estimar la distribución posterior conjunta. Así, la distribución marginal posterior de los hiperparámetros Ө se aproxima a través de una distribución gaussiana condicional a los efectos latentes. El modelo de regresión jerárquica se representa a partir de las siguientes ecuaciones:

                       ψ ~ π(ψ)                                 (1)

                     x | ψ ~ N(0,Q(ψ)^-1)                    (2)

             

donde Q(ψ) es la matriz de precisión (la inversa de la matriz de covarianza) del vector gaussiano latente x; η(x) = Ax representa la transformación lineal que mapea el vector latente x sobre los predictores η_{i =} η_i (x)  asociados a las observaciones y_i (Martino & Rue, 2010). La estructura de dependencia entre las observaciones y_i se captura a través de la matriz de precisión Q(ψ) sobre el campo latente x.

En nuestro estudio:

η_i=log(ϱ_i),

donde:

λ_i=E_i ϱ_i,

 

donde λ_i se define en términos de la tasa ϱ_i y del número esperado de casos E_i, el cual se estima por medio de:

y la tasa de pobreza municipal se define a partir de:

que es el cociente del número observado de personas en pobreza y_i y la población expuesta a riesgo de pobreza, misma que se modela con una distribución Poisson  y_i ∼ Poisson(λ_i) (Blangiardo et al., 2013).

La dependencia espacial se modela a través de la estructura de vecindades presente en los municipios del estado con base en la definición de vecino. Se dice que dos municipios son vecinos (de primer orden) cuando comparten una frontera común, y que son vecinos de segundo orden cuando algún vecino de primer orden comparte una forma común (Bivand et al., 2015).

Finalmente, el modelo de regresión gaussiano estructurado latente está dado por:

                                            η_i = β₀ + β₁ x_1i + u_i + v_i.                                   (4)

El parámetro β₀ cuantifica la tasa promedio de pobreza en el estado (Blangiardo & Cameletti, 2013). La parte espacial no estructurada se representa por v_i, cuya distribución está dada por:

,

mientras que u_i es la parte del modelo espacialmente estructurado condicional autorregresivo, cuya distribución es:

,

donde μ_i es la media del área i y s_i, la desviación estándar (Rue, Martino & Chopin, 2009), misma que depende del número de vecinos:

,

donde  controla la variación entre efectos aleatorios espacialmente estructurados, mientras que r_ij cuantifica la proximidad espacial (Bivand et al., 2015). β₁ representa la parte de efectos fijos del modelo. El coeficiente β₁ en su escala natural es el efecto que el incremento de una unidad de gasto social ejerce sobre el aumento de beta unidades del riesgo de padecer pobreza. Para el modelo representado por la ecuación (4), el vector de parámetros se da por θ = (β₀,β₁,f)y el vector de hiperparámetros, por ψ = {τ_u,τ_v}. Es importante señalar que la precisión se define como el inverso de la varianza  (Martins et al., 2012).

Tal como se definió en la ecuación (2), ψ conforma un campo aleatorio gaussiano markoviano (GMRF, por sus siglas en inglés), de manera que tiene una distribución normal multivariada con media μ y matriz de precisión Q(ψ). Los componentes de ψ se suponen condicionalmente independientes, lo cual implica que Q(ψ) es una matriz de precisión dispersa (Rue & Held, 2005). Este tipo de matrices permiten un cálculo numérico eficiente para operaciones que requieren de la descomposición LR, lo que genera beneficios computacionales importantes al momento de estimar el valor de los parámetros desconocidos, con la ventaja adicional de que la distribución posterior conjunta de los vectores de parámetros e hiperparámetros puede estimarse como el producto de la densidad del GMRF y la distribución previa del vector de hiperparámetros ψ (Rue, Matino & Chopin, 2009), ventajas que son utilizadas por el algoritmo implementado en INLA, paquete que fue utilizado para estimar los modelos expuestos.

 

Implementación

Una de las limitaciones más importantes a la hora de ejecutar los métodos de regresión bayesianos reside en su alto costo computacional, donde algoritmos como la cadena de Markov Monte Carlo (MCMC), Metropolis-Hasting y Gibbs sampling son utilizados de manera cotidiana para obtener la distribución posterior de distintos parámetros desconocidos (Blangiardo et al., 2013). En fecha reciente, se ha desarrollado una alternativa a los métodos tipo MCMC, cuya principal ventaja es ser computacionalmente eficiente; la alternativa INLA (Rue et al., 2009; Martino & Rue, 2010) genera soluciones analíticas eficientes, implementadas de forma numérica, cuya finalidad es aproximar la distribución posterior de los parámetros de modelos gaussianos estructurados latentes.

La modelación espacial de la pobreza municipal se realizó a través de la implementación del modelo (4), mismo que fue desarrollado en el paquete INLA disponible en lenguaje R (R Core Team, 2016), donde η_i es el valor esperado de la pobreza municipal y x₁ siginifics el gasto social municipal per cápita en miles de pesos; los betas representan la parte de efectos fijos; v_i, los efectos espaciales no estructurados; y u_i, la parte espacialmente estructurada del modelo.

Los parámetros estimados se identifican a través del vector de parámetros dado por Θ = {β₀, β₁, ξ₁, u). Es importante señalar que, para fines de interpretación, el paquete R-INLA reparametriza ξ₁ como (Martins et al., 2012):

                                  ξ_i=u_i+v_{i^.                                    (5)}

El valor predeterminado por defecto para la distribución previa de los parámetros está dado por un vector que sigue una distribución gaussiana (Blangiardo et al., 2013), que especifica la media y el inverso de la varianza (precisión). La definición previa del vector de hiperparámetros ψ = {τ_u,τ_v} se realizó a través del logaritmo de la precisión de efectos espaciales no estructurados dada como log = (τ_v) ∼ logGamma(1,0.0005) y el logaritmo de la precisión de los efectos espacialmente estructurados log = (τ_u) ∼ logGamma(1,0.0005) . El objetivo de las especificaciones es definir distribuciones a priori no informativas.

 

Resultados

La especificación del modelo (4) permite conocer la distribución espacial del riesgo de padecer pobreza. La estimación de los efectos fijos de este se presenta en el cuadro 2. En esta ocasión, el coeficiente β₀ carece de significado debido a que, si transformamos el parámetro a escala natural, se tendría que menos de 5 % de la población del estado de Chiapas estaría expuesta al riesgo de ser pobre. Es importante recordar que todos los parámetros estimados se encuentran en escala logarítmica, por lo que deben ser transformados antes de su interpretación.

 

 

Cabe señalar que el modelo (4) tiene como finalidad evaluar el efecto del gasto social sobre el riesgo de pobreza municipal. Los resultados indican que el incremento relativo de mil pesos de gasto social per cápita implicaría una reducción de 0.7 puntos porcentuales sobre el riesgo de ser pobre (ver cuadro 2), con lo cual se estima que su impacto sobre la pobreza se da en el sentido correcto, con una significancia estadística alta, pero menor a 1 punto porcentual.

Los efectos aleatorios estimados por el modelo (4) contienen información a nivel municipal de los efectos espaciales estructurados y no estructurados. Estos son recogidos por el vector ξ, que representa el riesgo relativo espacial expresado como:

ς_i = exp(ξ) = exp(u_i+v_i),

mismo que representa el riesgo residual relativo de cada municipio (comparado con la totalidad del estado) una vez descontado el efecto del gasto social (x₁).

Al igual que en los modelos de regresión convencionales, una de las formas más utilizadas para medir la calidad de ajuste de un modelo gaussiano estructurado latente es mediante la proporción de varianza explicada por el componente espacial estructurado u_i (que representa la variabilidad explicada a partir del componente condicional autorregresivo); dado que la varianza marginal del componente espacial no estructurado v_i no es directamente comparable (Rue, Martino & Chopin, 2009), resulta necesario obtener una estimación empírica de la varianza marginal posterior de los efectos estructurados, la cual suele aproximarse a partir de:

,

donde ū es el promedio de las u_i, la cual debe contrastarse con la varianza marginal posterior de los efectos no estructurados a partir de:

La estimación se realiza a través de una simulación de muestras tomadas de las distribuciones marginales posteriores. El procedimiento se encuentra implementado en R-INLA (Martino & Rue, 2010); en nuestra investigación se realizó una simulación de 10 mil casos extraídos de las distribuciones marginales de τ_v y τ_u para cada uno de los municipios.

La proporción de varianza espacial explicada resultó ser de 6.6 % para el modelo (4), lo cual sugiere que, a pesar del alto nivel de autocorrelación espacial bivariada estimado, la capacidad explicativa del gasto social sobre la pobreza fue inferior a 1 punto porcentual, por lo que la distribución espacial de un fenómeno como este no puede explicarse solo a través del gasto social, sino que se requiere de un conjunto mucho más amplio de factores.

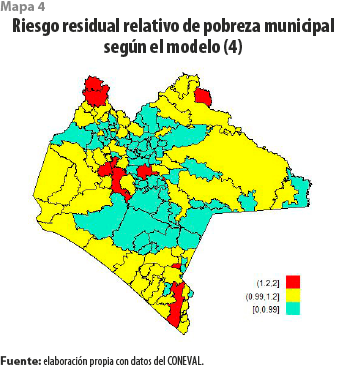
El mapa 4 muestra la media posterior del riesgo residual relativo ς de ser pobre en comparación con la totalidad del estado de Chiapas (Schrödle y Held, 2011). Los efectos observados presentan un patrón espacial de pobreza donde los municipios dibujados en colores rojo y amarillo se encuentran en mayor riesgo de ser pobres, en comparación con los restantes (verde).

 

 

La diferenciación espacial mostrada (mapa 4) pone en evidencia la importancia de la ubicación territorial al momento de determinar los municipios con mayor riesgo de sufrir pobreza. Es importante señalar que los municipios de Arriaga, Berriozábal, Cintalapa, Jiquipilas y Ocozocoautla configuran un conglomerado de alto riesgo de padecer pobreza una vez descontado el efecto del gasto social, situación que se contrapone al análisis de correlación espacial bivariada presentado en el mapa 3. Una situación similar se observa en el conglomerado de municipios en color rojo ubicados sobre la costa, tal como puede verse en el mapa 4.

 

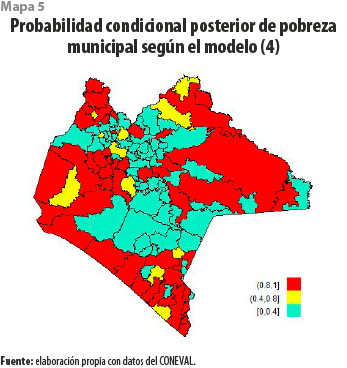
En el mapa 5 se aprecia la probabilidad posterior condicional P( ς_i > 1 |  y ) ~ P( ξ_i > 0 |  y ), que cuantifica el riesgo excesivo de ser pobre en el municipio i dado el nivel medio de pobreza observado en el estado, de manera que los municipios marcados en rojo muestran un patrón de exceso de riesgo de alcanzar niveles de pobreza superiores al promedio estatal, en especial para dos conglomerados de alta probabilidad sobre los municipios de la costa y la frontera con Oaxaca, lo que confirma el patrón observado en el mapa 4.

Los resultados presentados por los mapas 4 y 5 contrastan con los observados en el mapa 3, que configura un patrón de correlación espacial bivariado entre la pobreza y el gasto social, mismo que coloca en una categoría de autocorrelación espacial de baja-baja a los municipios anteriormente señalados, lo cual implica que se forma un conglomerado con bajos niveles de gasto social y de pobreza, sin embargo, algunos municipios en estas condiciones presentan una alta probabilidad de ser pobres, en términos del nivel medio de pobreza observado en el estado y una vez descontado el efecto del gasto social.

 

Conclusiones

El trabajo ofrece una primera aproximación a la modelación del efecto del gasto social sobre la distribución espacial de la pobreza en municipios de Chiapas, donde el gasto social resultó ser un factor importante para modelar el riesgo de pobreza municipal, sin embargo, a pesar de la enorme transferencia de recursos destinados a su combate, el incremento de mil pesos per cápita anuales (al FISM) reduciría únicamente en 0.7 puntos porcentuales el nivel de pobreza municipal, al 2015, por lo que la repercusión del gasto social en el bienestar de la gente dependería no solo del nivel de gasto, sino también del desempeño y calidad de los servicios ofertados, por lo que el diseño de políticas públicas debería considerar diferentes alternativas para mejorar la efectividad de los programas destinados al combate a la pobreza en el estado.

El análisis estadístico exploratorio de la relación entre la pobreza y el gasto social municipal muestra la existencia de un alto grado de correlación espacial (ver mapa 3), sin embargo, como se demostró a lo largo del trabajo, existen municipios en regiones de Chiapas expuestos a una alta probabilidad de padecer pobreza (ver mapa 5), y se trata de los mismos municipios donde el gasto social se encuentra por debajo del promedio estatal, lo que pone en evidencia la necesidad de modificar el monto y destino de dichos fondos.

El análisis espacial del gasto social permite identificar la forma en la que se distribuyen los recursos en el territorio y la manera en la que estos impactan a los municipios expuestos a mayores niveles de pobreza; para ello, es importante contar con información actualizada y geográficamente desagregada, que permitirá conocer la distribución espacial tanto de los fondos destinados al gasto social como de su efecto en términos de reducción de los niveles de pobreza.

Finalmente, cabe reconocer que el éxito de la estimación del modelo de regresión gaussiano latente se debe, en gran medida, a la aproximación integrada anidada de Laplace implementada en el paquete R-INLA, que proporciona importantes ventajas computacionales que permiten estimar eficientemente el modelo.

____________

Fuentes

Anselin, L. “Local Indicators of Spatial Associations-LISA”, en: Geographical Analysis. Vol. 27, 1995, pp. 93-115.

Bivand, Roger, Virgilio Gómez Rubio, & Rue Håvard. “Spatial Data Analysis with R-INLA with Some Extensions”, en: Journal of Statistical Software. 63, 2015, pp. 1-31.

Blangiardo, M. y M. Cameletti. Bayesian Spatio and Spatio-Temporal Models with R-INLA. Wiley, 2013.

Blangiardo, M., Michela Cameletti, Gianluca Baio and Håvard Rue. “Spatial and spatio-temporal models with R-INLA”, en: Spatial and Spatio-temporal Epidemiology. Volume 4, 2013, pp. 33-49.

Barrientos, J., W. Gómez, & R. Renhals. “Crecimiento, distribución y pobreza en América Latina: un ejercicio de panel, 1990-2005”, en: Perfil de Coyuntura Económica. 11, Universidad de Antioquia, 2008.

Barro, R. “Economic growth in a cross-section of countries”, en: Quarterly Journal of Economics. 106(2), 1991, pp. 407-433.

Cortés, F. Gasto social y pobreza. Documento de trabajo. Programa Universitario de Estudios de Desarrollo. México, D. F., UNAM, 2009.

Centro de Estudios de las Finanzas Públicas (CEFP). La pobreza y el gasto social en México. México, Cámara de Diputados, LXIII Legislatura, 2015.

Chasco, C. Econometría espacial aplicada a la predicción-extrapolación de datos microterritoriales. Madrid, Consejería de Economía e Innovación Tecnológica, Comunidad de Madrid, 2003.

CONEVAL. Metodología para la medición multidimensional de la pobreza en México. Segunda edición. México, D. F., CONEVAL, 2014.

_______ Metodología para la medición de la pobreza en los municipios de México, 2015. México, CONEVAL, 2017.

Cliff, A. D. y J. K. Ord. Spatial processes: Models and Applications. London, Pion Limited, 1981.

Cressie, N. Statistics for spatial data. New York, John Wiley, 1993.

Ferreira, F., P. Leite, & M. Ravallion. “Poverty reduction without economic growth? Explaining Brazil's poverty dynamics, 1985-2004”, en: Journal of Development Economics. 93, 2010, pp. 20-36.

Getis, A. y J. K. Ord. “The analysis of spatial association by use of distance statistics”, en: Geographical Analysis. 24, 1992, pp. 189-199.

López, Jorge y Gerardo Núñez. Desigualdad y exclusión social en Chiapas, una mirada a largo plazo. OXFAM México, 2016.

Martino, S. y H. Rue. Implementing Approximate Bayesian Inference using Integrated Nested Laplace Approximation: a manual for the INLA program. Department of Mathematical Sciences, Norwegian University of Science and Technology, 2010.

Martins, G., D. Simpson, F. Lindgren y H. Rue. Bayesian computation with INLA: new features. Norwegian University of Science and Technology Report, 2012.

R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria, R Foundation for Statistical Computing, 2016.

Rue, H. y L. Held. Gaussian Markov Random Fields. Theory and Applications. Chapman & Hall, 2005.

Rue, H., S. Martino y N. Chopin. “Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations”, en: Journal of the Royal Statistical Society Series B. 71 (2), 2009, pp. 1-35.

Schrödle, B. y L. Held. “Spatio-temporal disease mapping using INLA”, en: Environmetrics. 22 (6), 2011, pp. 725-734.

Tobler, W. R. “A computer movie simulating urban growth in the Detroit region”, en: Economic Geography. 46(Supplement), 1970, pp. 234-240.

^[1]  Los fondos constituidos con recursos del Ramo 33 son: I. Fondo de Aportaciones para la Educación Básica y Normal; II. Fondo de Aportaciones para los Servicios de Salud; III. Fondo de Aportaciones para la Infraestructura Social (Estatal y Municipal); IV. Fondo de Aportaciones para el Fortalecimiento de los Municipios y de las Demarcaciones Territoriales del Distrito Federal (FORTAMUN); V. Fondo de Aportaciones Múltiples; VI. Fondo de Aportaciones para la Educación Tecnológica y de Adultos; VII. Fondo de Aportaciones para la Seguridad Pública de los Estados y del Distrito Federal; y VIII. Fondo de Aportaciones para el Fortalecimiento de las Entidades Federativas.

^[2] El Fondo para la Infraestructura Social Municipal (FISM) junto con el Fondo de Aportaciones para el Fortalecimiento de los Municipios y las Demarcaciones Territoriales del Distrito Federal (FORTAMUN) son los únicos dos fondos del Ramo 33 que son ejercidos directamente por los municipios, sin embargo, no fue posible disponer de las cifras a nivel municipal del fondo FORTAMUN.

^[3] El Índice de Moran se construye en dos versiones, Moran Global y Moran Local; la diferencia radica en que el primero es una medida de autocorrelación espacial para todas las regiones analizadas y la segunda mide el grado de autocorrelación entre una región y sus vecinos. En ambos casos, la correlación se estima considerando la distancia y un atributo y.